Carregando, aguarde alguns segundos.
1 - Distribuições com Seaborn
Visualize Distribuições com o módulo Seaborn.
Seaborn é uma biblioteca que usa o Matplotlib para plotar gráficos. Ele será usado para visualizar distribuições aleatórias.
Autores
Roberto Teixeira
Betobyte
Cientista de Dados
CIEDA
cieda.com.br
roberto@cieda.com.br

Autor
Carlos Delfino
Arduino
Cientista de Dados
Basicão da Eletrônica
www.carlosdelfino.eti.br
consultoria@carlosdelfino.eti.br

Coautor
1.1 - Instale o Seaborn.
1.2 - Distplots
1.3 - Importar Matplotlib
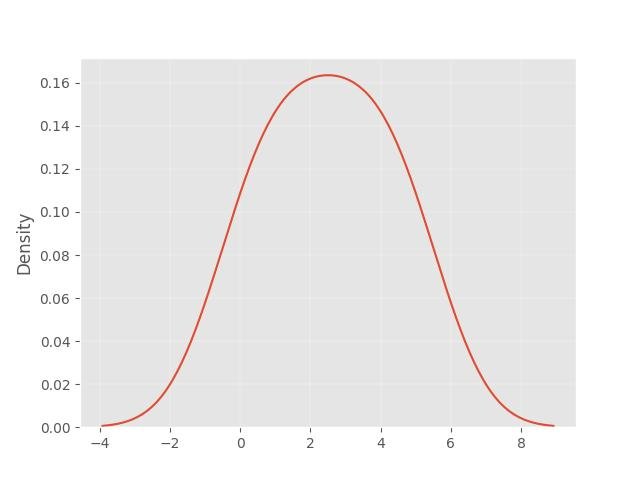
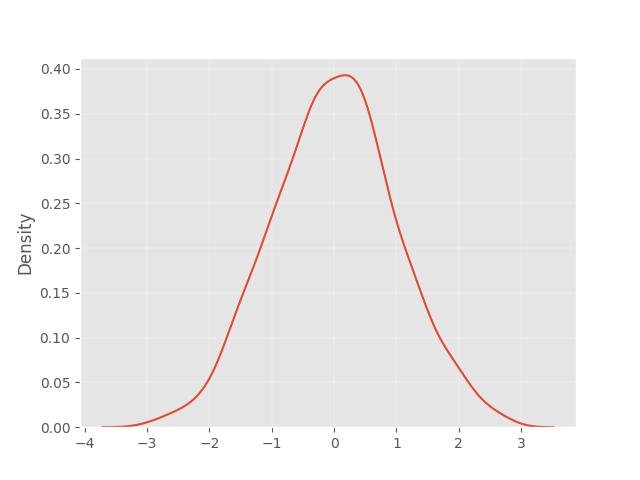
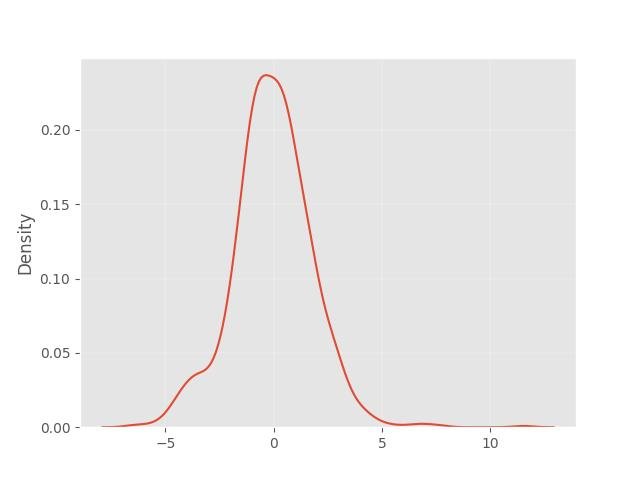
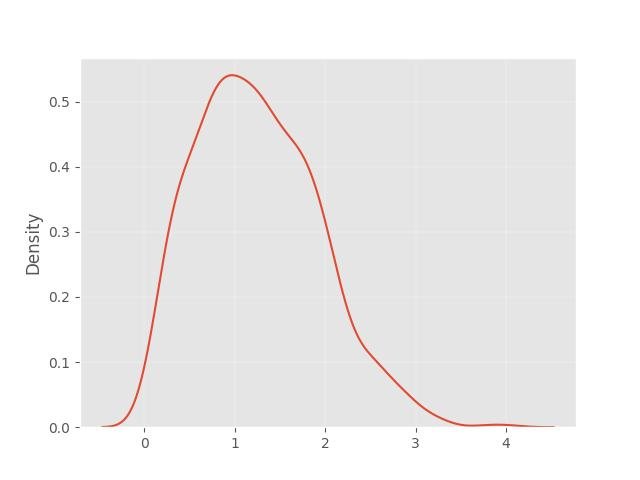
1.4 - Distribuição Normal (Gaussiana)
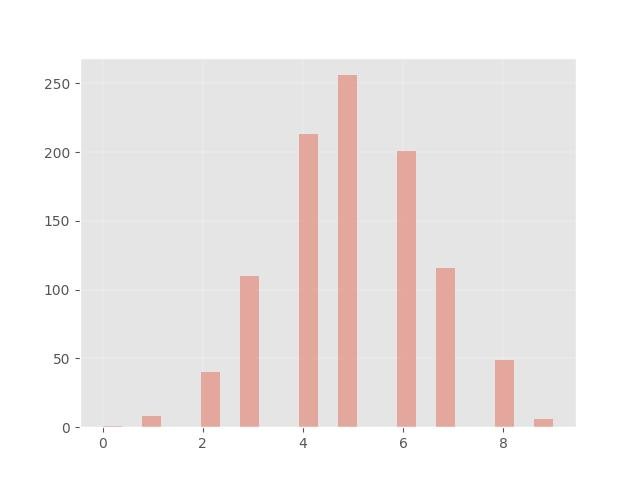
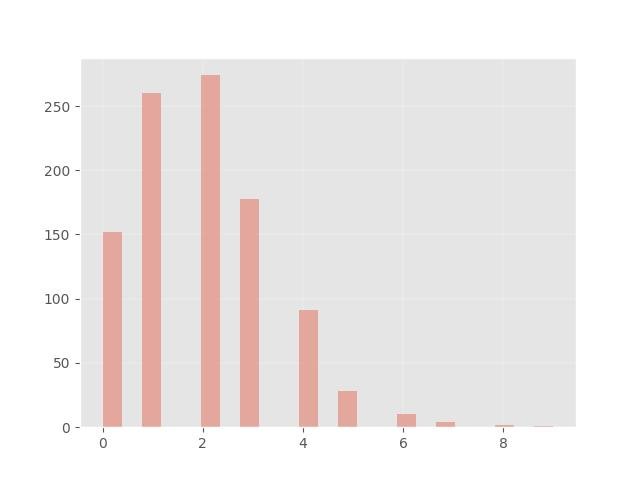
1.5 - Distribuição binomial
1.6 - Visualização da Distribuição Binomial
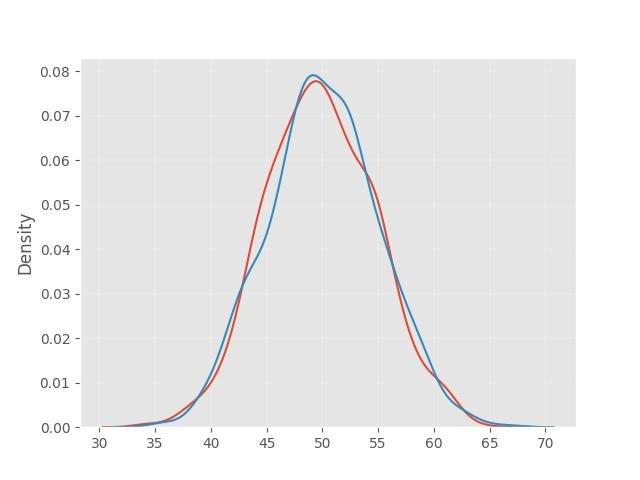
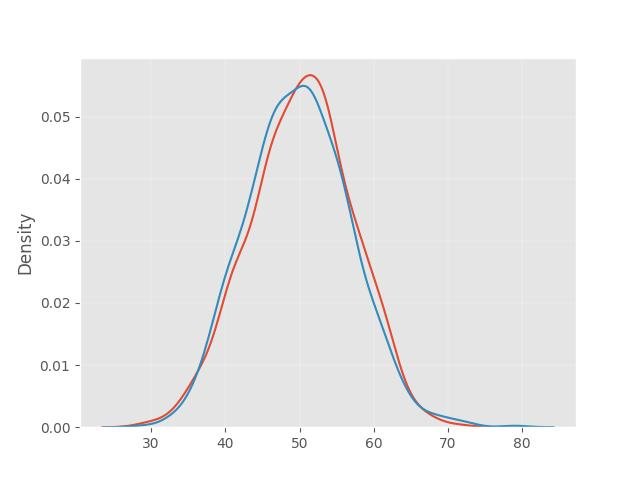
1.7 - Diferença entre distribuição normal e binomial
1.8 - Distribuição de Poisson
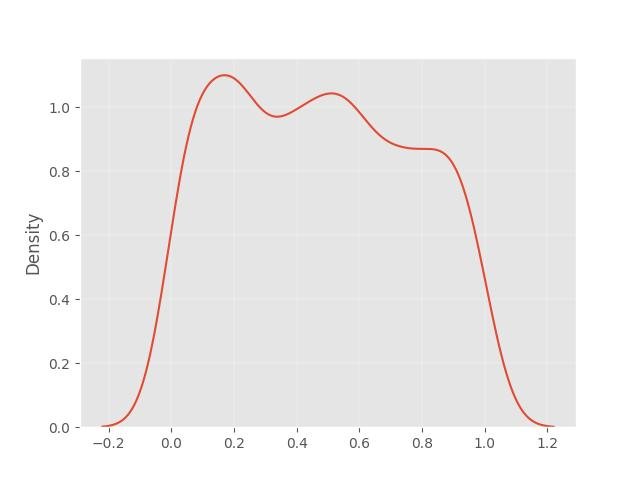
1.9 - Distribuição uniforme
1.10 - Distribuição Logística
1.11 - Distribuição Multinomial
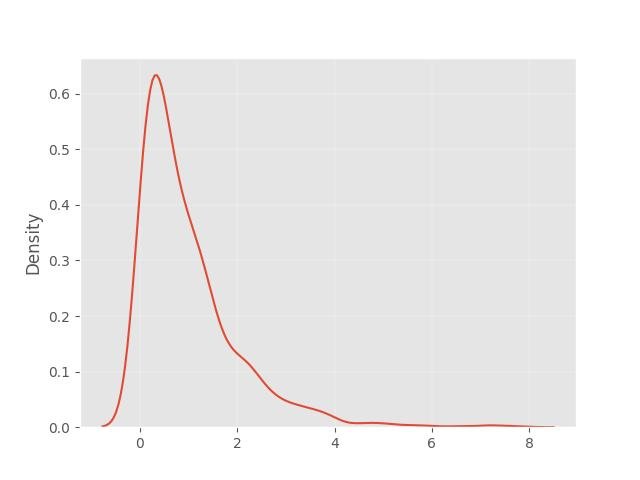
1.12 - Distribuição Exponencial
1.13 - Distribuição do Quiquadrado
1.14 - Distribuição Rayleigh
1.15 - Distribuição de Pareto
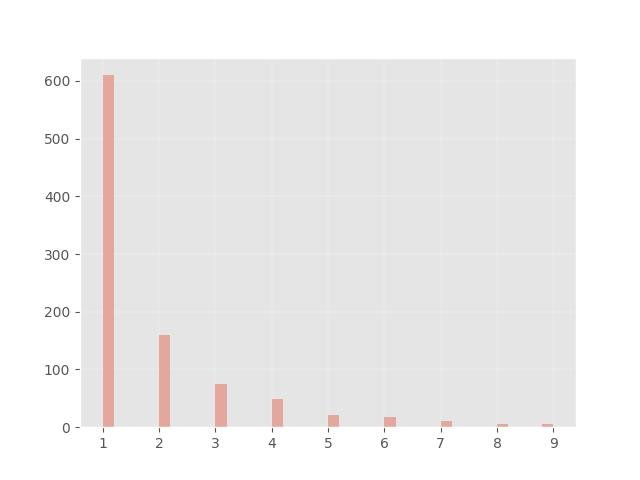
1.16 - Distribuição Zipf

Arduino
Coautor

Betobyte
Autor
Autores