6 - Programação Quântica com Qiskit
O Qiskit é uma biblioteca para o Python, com código aberto, para programação quântica.
Desenvolvida pela IBM, disponibiliza uma linguagem baseada no Python que permite aos usuários criarem e executarem programas quânticos em computadores quânticos reais ou simulados.
O pacote para Python da biblioteca do Qiskit, um dos mais populares disponíveis atualmente na comunidade quântica, é amplamente usado e oferece uma variedade de ferramentas e recursos para programação quântica, incluindo simulação de circuitos quânticos, acesso a hardware quântico real e suporte a diferentes plataformas de hardware.
Qiskit oferece suporte para operações lógicas quânticas, como a operação de portas quânticas, medições e emaranhamento. Além disso, a linguagem possui uma grande comunidade de usuários e uma vasta documentação, o que facilita o aprendizado e o desenvolvimento de programas.
6.1 - Programas com circuitos e operações quânticos
Os programas quânticos no Qiskit são normalmente expressos por meio de circuitos quânticos, que são representações visuais de sequências de operações quânticas aplicadas a qubits. Esses circuitos são construídos usando a classe QuantumCircuit do pacote Qiskit.
from qiskit import QuantumCircuit # Importamos a classe QuantumCircuit no pacote Qiskit
qc = QuantumCircuit(2) # Criamos um circuito quântico com 2 <i>qubits</i>Principal classe para criar e manipular circuitos quânticos no Qiskit, fornece métodos para adicionar qubits aos circuitos, aplicar operações quânticas nesses qubits e realizar medições. Os circuitos quânticos são construídos passo a passo adicionando portas ou operações aos qubits no circuito.
As operações quânticas, também conhecidas como portas quânticas, são representadas no Qiskit pelas classes que são descendentes da classe Instruction. Essas classes incluem operações básicas como X, Y, Z, H, CX (porta CNOT) e muitas outras. Além disso, o Qiskit permite a criação de operações personalizadas estendendo a classe Instruction.
Para adicionar uma operação quântica a um circuito quântico, utiliza-se o método correspondente da classe QuantumCircuit. Por exemplo, para adicionar uma porta Hadamard (H) a um qubit no circuito, utiliza-se o método h(qubit) do objeto QuantumCircuit. O código seria assim:
qc = QuantumCircuit(2) # Cria um circuito quântico com 2 <i>qubits</i>
qc.h(0) # Aplica a porta Hadamard no primeiro <i>qubit</i>Os circuitos quânticos permitem a composição e combinação de várias operações quânticas para criar algoritmos e executar tarefas específicas. Além disso, é possível realizar medições nos qubits usando o método measure(q,c) do circuito, onde q é o qubit a ser medido e c é o bit clássico em que o resultado da medição será armazenado.
Com a classe QuantumCircuit e as classes de operações quânticas descendentes da classe Instruction, os usuários do Qiskit podem construir circuitos quânticos personalizados, aplicar operações quânticas padrão e realizar medições nos resultados. Isso permite a implementação de algoritmos quânticos e a exploração de fenômenos e propriedades quânticas.
Em resumo, os circuitos quânticos no Qiskit são construídos usando a classe QuantumCircuit e as operações quânticas são representadas por classes descendentes da classe Instruction. Essa combinação de circuitos e operações quânticas permite a criação e execução de programas quânticos no Qiskit.
Construção de Circuitos Quânticos
Um circuito quântico pode ser criado fornecendo-se um argumento que indica o número de fios quânticos desejados (qubits) para esse circuito. Isso geralmente é fornecido como um número inteiro.
Primeiro, importamos o pacote qiskit em nosso programa Python:
from qiskit import QuantumCircuitO código a seguir cria uma instância da classe QuantumCircuit com dois qubits:
qc = QuantumCircuit(2)Opcionalmente, o número desejado de fios clássicos (bits) também podem ser especificados. O primeiro argumento refere-se ao número de fios quânticos e o segundo argumento ao número de fios clássicos:
qc = QuantumCircuit(2,2)O número de fios quânticos e clássicos desejados também pode ser expresso fornecendo-se instâncias de QuantumRegister e ClassicalRegister como argumentos para QuantumCircuit.
Circuitos Quânticos Parametrizados
Às vezes é útil criar-se um circuito quântico no qual os valores possam ser fornecidos em tempo de execução.
Esta capacidade está disponível no Qiskit usando circuitos parametrizados, implementados em parte pelas classes Parameter e ParameterVector.
Criando uma instância de parâmetro
A classe Parameter é usada para representar um parâmetro em um circuito quântico.
Conforme mostrado nesse exemplo, um parâmetro pode ser criado fornecendo uma string unicode para seu construtor da seguinte maneira:
theta1 = Parameter("θ¸1")A referência de objeto da classe Parameter nomeada theta1 pode ser usada subseqüentemente no método bind_parameters() ou, alternativamente, no assign_parameters() da classe QuantumCircuit.
6.2 - Principais Classes do Qiskit
O Qiskit disponibiliza uma ampla gama de ferramentas e funcionalidades para desenvolver, simular e executar algoritmos quânticos em diferentes plataformas e dispositivos. O Qiskit é uma biblioteca em Python que permite que os usuários criem e manipulem circuitos quânticos, executem simulações, acessem computadores quânticos reais e realizem tarefas relacionadas à computação quântica.
O esquema a seguir apresenta as principais classes e seus relacionamentos:
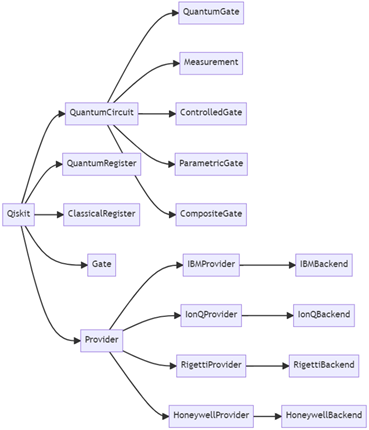
Classe QuantumCircuit
A classe QuantumCircuit é a principal classe para criar e manipular circuitos quânticos no Qiskit. Ela representa um circuito quântico, que é uma sequência ordenada de operações quânticas aplicadas a qubits. Essas operações quânticas são representadas por portas quânticas, como a porta Hadamard (H), a porta CNOT (CX), a porta Rz, entre outras.
Ao criar uma instância da classe QuantumCircuit, podemos especificar o número de qubits que o circuito terá. Por exemplo, podemos criar um circuito com 3 qubits da seguinte forma:
from qiskit import QuantumCircuit
qc = QuantumCircuit(3)Podemos então adicionar operações quânticas a esse circuito utilizando os métodos fornecidos pela classe QuantumCircuit. Por exemplo, para aplicar uma porta Hadamard ao primeiro qubit e uma porta CNOT entre o primeiro e o segundo qubit, podemos fazer o seguinte:
qc.h(0) # Aplica a porta Hadamard ao primeiro <i>qubit</i>
qc.cx(0, 1) # Aplica a porta CNOT entre o primeiro e o segundo <i>qubit</i>Além das portas quânticas básicas, o Qiskit oferece uma variedade de outras operações quânticas e técnicas de composição de circuitos para construir algoritmos quânticos mais complexos. Também é possível realizar medições em qubits específicos usando o método measure(qubit, bit) do circuito.
Os circuitos quânticos construídos com a classe QuantumCircuit podem ser executados em simuladores locais ou em computadores quânticos reais por meio dos provedores disponíveis no Qiskit. Para executar um circuito, é necessário fornecer um backend adequado, que pode ser um simulador ou um dispositivo quântico real.
A classe QuantumCircuit também oferece métodos para visualizar o circuito, obter informações sobre suas propriedades e converter o circuito para uma representação em formato QASM (Quantum Assembly Language), que é uma linguagem de baixo nível para descrever circuitos quânticos.
Classe QuantumRegister
A classe QuantumRegister do Qiskit representa um registro de qubits em um circuito quântico. Um registro quântico é um conjunto de qubits que podem ser usados para armazenar e manipular informações quânticas. Essa classe permite definir o número de qubits em um registro e atribuir nomes a esses qubits.
Ao criar uma instância da classe QuantumRegister, podemos especificar o número de qubits que o registro terá. Por exemplo, podemos criar um registro quântico com 3 qubits da seguinte forma:
from qiskit import QuantumRegister
qreg = QuantumRegister(3)Podemos então utilizar esse registro quântico ao construir um circuito quântico com a classe QuantumCircuit. Por exemplo, podemos criar um circuito quântico com um registro quântico de 3 qubits da seguinte forma:
from qiskit import QuantumCircuit, QuantumRegister
qreg = QuantumRegister(3)
qc = QuantumCircuit(qreg)Podemos então adicionar operações quânticas a esse circuito, aplicando gates quânticos aos qubits do registro. Por exemplo, para aplicar uma porta Hadamard ao primeiro qubit do registro, podemos fazer o seguinte:
qc.h(qreg[0]) # Aplica a porta Hadamard ao primeiro qubit
Além de permitir a criação de circuitos quânticos, a classe QuantumRegister oferece métodos e atributos para acessar informações sobre o registro, como o número de qubits e os nomes atribuídos a eles. Alguns desses métodos e atributos incluem:
- size(): Retorna o número de qubits no registro.
- qubits(): Retorna uma lista de todos os qubits no registro.
- name: Atributo que permite obter e definir o nome do registro.
A classe QuantumRegister é parte integrante do Qiskit e desempenha um papel importante na construção e manipulação de circuitos quânticos. Ela permite a criação de registros quânticos com um número específico de qubits e oferece uma interface conveniente para acessar e manipular os qubits nesses registros.
Classe ClassicalRegister
A classe ClassicalRegister do Qiskit representa um registro clássico em um circuito quântico, usado para armazenar os resultados de medições feitas em qubits durante a execução de um circuito quântico. Essa classe permite definir o número de bits em um registro clássico e atribuir nomes a esses bits.
Ao criar uma instância da classe ClassicalRegister, podemos especificar o número de bits que o registro terá. Por exemplo, podemos criar um registro clássico com 3 bits da seguinte forma:
from qiskit import ClassicalRegister
creg = ClassicalRegister(3)Podemos então utilizar esse registro clássico ao construir um circuito quântico com a classe QuantumCircuit. Por exemplo, podemos criar um circuito quântico com um registro clássico de 3 bits da seguinte forma:
from qiskit import QuantumCircuit, ClassicalRegister
creg = ClassicalRegister(3)
qc = QuantumCircuit(creg)Durante a execução do circuito, podemos medir qubits específicos e armazenar os resultados nessas posições do registro clássico usando o método measure(qubit, bit) do circuito. Por exemplo, para medir o qubit no índice 0 e armazenar o resultado no bit no índice 2 do registro clássico, podemos fazer o seguinte:
qc.measure(0, 2)
# Mede o <i>qubit</i> no índice 0 e armazena o resultado
# no bit no índice 2 do registro clássicoAlém de permitir a criação de circuitos quânticos, a classe ClassicalRegister oferece métodos e atributos para acessar informações sobre o registro, como o número de bits e os nomes atribuídos a eles. Alguns desses métodos e atributos incluem:
- size(): Retorna o número de bits no registro.
- bits(): Retorna uma lista de todos os bits no registro.
- name: Atributo que permite obter e definir o nome do registro.
A classe ClassicalRegister é parte integrante do Qiskit e desempenha um papel importante na construção e manipulação de circuitos quânticos, permitindo a criação de registros clássicos com um número específico de bits e oferece uma interface conveniente para acessar e armazenar resultados de medições durante a execução de um circuito quântico.
Classe Gate
A classe Gate é uma classe abstrata do Qiskit, o que significa que não pode ser instanciada diretamente, representando uma operação quântica em um circuito quântico. Esta classe serve de base para todas as classes específicas de portas, como XGate, HGate, CNOTGate, entre outras, que representam portas e operações quânticas individuais.
A classe Gate define os métodos e atributos básicos comuns a todas as portas. Isso inclui o método __init__(), que é responsável por inicializar a porta, e o método qasm(), que retorna a representação da porta em linguagem QASM (Quantum Assembly Language). Além disso, a classe Gate possui outros métodos e atributos, como:
- name: Atributo que representa o nome da gate.
- params: Atributo que representa os parâmetros da gate.
- num_qubits: Atributo que representa o número de qubits que a gate atua.
- label: Atributo opcional que permite adicionar um rótulo à gate.
Ao criar uma instância de uma classe de porta específica, podemos então utilizá-la para adicionar operações quânticas aos circuitos quânticos. Por exemplo, para adicionar uma porta X (NOT) a um circuito, podemos fazer o seguinte:
from qiskit import QuantumCircuit
from qiskit.extensions import XGate
circuito = QuantumCircuit(1)
porta_x = XGate()
circuito.append(porta_x,[0])A classe Gate é uma parte fundamental do Qiskit, permitindo que os usuários construam e manipulem circuitos quânticos usando uma variedade de portas e operações quânticas. Ela fornece uma estrutura unificada para representar e trabalhar com portas individuais em circuitos quânticos.
Classe Provider
A classe Provider é uma classe fundamental no Qiskit que representa um provedor de serviços quânticos. Um provedor é uma entidade que oferece acesso a recursos quânticos, como simuladores ou computadores quânticos reais. O Qiskit suporta vários provedores, como o AerProvider para simulações locais e o IBMQProvider para acesso aos dispositivos quânticos da IBM e provedores de terceiros.
A classe Provider possui métodos e atributos que permitem aos usuários listar os serviços disponíveis, obter informações sobre os provedores e acessar os recursos quânticos fornecidos por eles. Alguns dos métodos e atributos comuns da classe Provider incluem:
- backends(): retorna uma lista de todos os recursos quânticos (backends) disponíveis no provedor.
- get_backend(name): retorna um objeto backend específico com base no seu nome.
- get_provider_name(): retorna o nome do provedor.
- available_backends(): retorna uma lista dos backends disponíveis atualmente.
Ao usar o Qiskit, os usuários podem criar uma instância de um provedor específico, como o AerProvider ou o IBMQProvider, e acessar os backends disponíveis por meio desse provedor. Isso permite que os usuários escolham entre diferentes provedores e backends, dependendo de suas necessidades e recursos disponíveis.
A classe Provider é parte integrante do Qiskit e desempenha um papel importante na conexão com os recursos quânticos disponíveis, fornecendo uma interface consistente para acessar os backends, permitindo que os usuários explorem diferentes plataformas e serviços quânticos sem a necessidade de interagir diretamente com implementações específicas de provedores.
6.3 - Execução dos programas quânticos com Qiskit
Programas quânticos são algoritmos e circuitos quânticos projetados para serem executados em computadores quânticos, escritos utilizando-se bibliotecas e frameworks quânticos, como o Qiskit, que fornecem uma interface para a construção e execução de circuitos quânticos.
Existem duas opções principais para execução de programas quânticos: em computadores quânticos reais e em simuladores quânticos.
- Computadores quânticos reais: os computadores quânticos reais são sistemas físicos que implementam qubits e permitem a execução de algoritmos quânticos. Esses computadores são fornecidos por provedores de serviços quânticos, como o IBM Quantum, IonQ, Rigetti e outros. Para executar um programa quântico em um computador quântico real, é necessário enviar o circuito quântico para o provedor de serviço por meio da interface do Qiskit. O provedor processará a solicitação e executará o circuito no hardware quântico. Os resultados da execução são então retornados ao usuário. No entanto, vale ressaltar que a disponibilidade de computadores quânticos reais pode ser limitada devido à demanda e aos recursos disponíveis.
- Simuladores quânticos: os simuladores quânticos são ambientes de software que emulam o comportamento de circuitos quânticos em um computador clássico. Esses simuladores permitem a execução de programas quânticos em um ambiente controlado, sem a necessidade de acesso a um computador quântico real. O Qiskit fornece um conjunto de simuladores quânticos, como o AerSimulator, que oferece diferentes métodos de simulação, como simulação de estado de vetor completo, simulação estocástica e simulação de amostragem. Ao executar um programa quântico em um simulador, o circuito quântico é processado, retornando os resultados simulados com base nas operações do circuito.
Ambas as opções têm vantagens e desvantagens. A execução em computadores quânticos reais oferece a oportunidade de experimentar algoritmos em hardware real, levando em consideração os efeitos do ruído e das limitações do sistema. Porém, o acesso a esses computadores pode ser limitado e as execuções podem levar mais tempo devido à demanda. Por outro lado, os simuladores quânticos oferecem um ambiente controlado para experimentação rápida e repetida, permitindo a depuração e o desenvolvimento de algoritmos sem as restrições de recursos dos computadores quânticos reais.
Simulador: AerSimulator Backend
O AerSimulator Backend (AerSB) é um dos backends disponíveis no módulo Aer do pacote qiskit, projetado para simular circuitos quânticos em computadores clássicos.
O AerSB fornece uma simulação de alto desempenho para circuitos quânticos, permitindo que os usuários executem e testem seus algoritmos quânticos em um ambiente simulado antes de realizar experimentos reais em hardware quântico.
O AerSB é particularmente útil quando se deseja executar circuitos quânticos em um ambiente controlado, onde é possível ter uma visão detalhada do estado quântico do sistema, em cada etapa da simulação. Ele permite que os usuários configurem diferentes parâmetros, como o número de shots (repetições do circuito), as condições iniciais do sistema quântico e até mesmo a inclusão de ruído simulado para simulações mais realistas.
Uma das principais vantagens do AerSB é sua velocidade de simulação. Ele utiliza algoritmos e otimizações avançadas para acelerar a execução de circuitos quânticos, permitindo a simulação de circuitos com um grande número de qubits e portas em um tempo razoável.
Além disso, o AerSB fornece suporte para uma variedade de métodos de simulação, como simulação de estado de vetor completo, simulação de matriz densa, simulação estocástica e simulação de amostragem. Esses métodos permitem que os usuários obtenham diferentes tipos de informações sobre o estado quântico do sistema, como a distribuição de probabilidade das medições e a evolução temporal do estado quântico.
Embora o AerSB seja um ambiente de simulação poderoso, é importante observar que ele não representa as limitações e o comportamento real de um computador quântico. Portanto, as simulações realizadas no AerSB podem não refletir completamente o desempenho e os resultados que seriam obtidos em um hardware quântico real.
No geral, o AerSB é uma ferramenta valiosa para simulação e desenvolvimento de algoritmos quânticos, permitindo aos usuários testarem seus circuitos quânticos em um ambiente simulado controlado, e assim acelerando o processo de desenvolvimento e depuração de algoritmos antes da implementação em hardware quântico.
Aqui está um exemplo de código Python usando o AerSB no Qiskit:
from qiskit import QuantumCircuit, transpile, assemble, Aer
# Criar um circuito quântico
qc = QuantumCircuit(2)
qc.h(0)
qc.cx(0, 1)
qc.measure_all()
# Transpilar o circuito para o AerSimulator backend
simulador = Aer.get_backend('aer_simulator')
circuito_compilado = transpile(qc, simulator)
# Executar o circuito no AerSimulator backend
job = simulador.run(assemble(circuito_compilado))
# Obter os resultados da simulação
resultado = job.result()
contagem = resultado.get_counts()
print(contagem)Neste exemplo:
- Primeiro criamos um circuito quântico qc com dois qubits.
- Em seguida, aplicamos a porta Hadamard (H) ao primeiro qubit
- Aplicamos a porta CNOT (CX) entre os dois qubits.
- Adicionamos uma medição de todos os qubits.
- Utilizamos a função transpile() para transpilar o circuito qc para o formato adequado para o AerSB. A variável simulador é definida como o objeto do backend AerSB, obtido através da chamada Aer.get_backend('aer_simulator').
- Utilizamos a função assemble() para montar o circuito transpilado em um objeto QASM que pode ser executado no backend.
- Executamos o circuito no backend com o método run() e retornamos o resultado em job.
- Utilizamos o método result() para obter o resultado da simulação e a função get_counts() do objeto para obter as contagens resultantes da medição.
- Por fim, as contagens são impressas no console.
Este exemplo demonstra como utilizar um objeto AerSB para simular um circuito quântico e obter os resultados da simulação.
O AerSB é um apenas simulador rodando em computadores clássicos, e não necessariamente refletirá o comportamento real de um computador quântico.
A variável resultado recebe o objeto da classe Result com os dados retornados:
Result(
backend_name='qasm_simulator',
backend_version='0.11.2',
qobj_id='2f8a7289-9b38-4454-9a09-d9ca2f9672fb',
job_id='6c2aa633-c73c-4558-9533-84999dedebd5',
success=True,
results=[
ExperimentResult(
shots=1,
success=True,
meas_level=2,
data=ExperimentResultData(counts={'0x0': 1}),
header=QobjExperimentHeader(clbit_labels=[
['c',0],['c',1],['c',2],['c',3]],
creg_sizes=[['c',4]],
global_phase=0.0,
memory_slots=4,
metadata={},
n_qubits=4,
name='circuit-88',
qreg_sizes=[['q',4]],
qubit_labels=[['q',0],['q',1],['q',2],['q',3]]
),
status=DONE,
seed_simulator=1701165717,
metadata={
'batched_shots_optimization': False,
'method': 'stabilizer',
'active_input_qubits': [0,1,2,3],
'device': 'CPU',
'remapped_qubits': False,
'num_qubits': 4,
'num_clbits': 4,
'sample_measure_time': 0.0008794,
'input_qubit_map': [[0,0],[1,1],[2,2],[3,3]],
'measure_sampling': True,
'noise': 'ideal',
'parallel_shots': 1,
'parallel_state_update': 8,
'fusion': {'enabled': False}
},
time_taken=0.0465539)
],
date=2023-06-08T11:13:36.375317,
status=COMPLETED,
header=QobjHeader(
backend_name='qasm_simulator',
backend_version='0.11.2'
),
metadata={
'parallel_experiments': 1,
'omp_enabled': True,
'max_memory_mb': 16271,
'max_gpu_memory_mb': 0,
'num_processes_per_experiments': 1,
'time_taken_load_qobj': 0.0656051,
'mpi_rank': 0,
'num_mpi_processes': 1,
'time_taken_execute': 0.0466742,
'time_taken': 0.1122974
},
time_taken=0.11249518394470215)6.4 - Classe QuantumCircuit
A classe QuantumCircuit é um componente fundamental no Qiskit, uma biblioteca de computação quântica em Python. Ela representa um circuito quântico composto por uma sequência de instruções e portas que operam em qubits e bits clássicos. A classe QuantumCircuit fornece uma interface poderosa para construir, manipular e simular circuitos quânticos.
Uma das principais características da classe QuantumCircuit é sua flexibilidade na construção de circuitos quânticos. Ela permite adicionar qubits e bits clássicos, anexar portas e instruções, realizar medições, ‘resetar’ qubits e muito mais. Com uma ampla variedade de métodos e atributos disponíveis, é possível construir circuitos quânticos complexos e personalizados para diferentes aplicações.
Além disso, a classe QuantumCircuit possui recursos avançados, como a capacidade de converter o circuito em uma porta ou instrução reutilizável usando os métodos to_gate() e to_instruction(). Isso permite a composição e reutilização de partes do circuito em outros circuitos, facilitando a construção de circuitos maiores e mais complexos.
A classe QuantumCircuit também oferece suporte a diversas operações, como inversão de circuito, validação de circuito, desenho visual do circuito e cálculo da representação matricial unitária do circuito. Essas funcionalidades são úteis para verificar a corretude do circuito, obter insights visuais sobre sua estrutura e realizar análises mais avançadas.
Além disso, a classe QuantumCircuit é compatível com os backends do Qiskit, permitindo a execução de circuitos em hardware quântico ou simuladores. Ela fornece métodos para envio de circuitos para execução, obtenção de resultados e manipulação dos resultados retornados.
A classe QuantumCircuit no Qiskit é uma poderosa ferramenta para construir e manipular circuitos quânticos. Com uma ampla gama de métodos e atributos, ela oferece flexibilidade e controle para projetar circuitos personalizados, além de suporte para validação, visualização e execução em hardware quântico ou simuladores. A classe QuantumCircuit é uma peça fundamental no desenvolvimento de algoritmos e aplicações na área da computação quântica.
Instanciação de objetos da classe QuantumCircuit
Abaixo temos o exemplo de código declarando uma variável qc, apontando para um objeto da classe QuantumCircuit, contendo quatro fios quânticos:
from qiskit import QuantumCircuit
qc = QuantumCircuit(4)Métodos da classe QuantumCircuit
| Nome | Nota |
|---|---|
| __init__(*regs[, nome, fase_global, metadados]) | Inicializar auto. |
| add_bits(bits) | Adicionar bits ao circuito. |
| add_calibration(porta, qubits, agendamento[, parâmetros]) | Registra uma definição de pulso personalizada de baixo nível para o portão especificado. |
| add_register(*regs) | Adicionar um registrador de qubits ou de bits clássicos ao circuito. |
| append(instrução [, qargs, cargs]) | Acrescentar uma ou mais instruções ao final do circuito, modificando o circuito no local e agindo nos qubits especificados. |
| assign_parameters(parâmetros[, local, …]) | Atribuir novos parâmetros ou valores. |
| barrier(*qargs) | Colocar uma barreira em um circuito quântico, fornecendo a separação funcional entre portas. |
| bind_parameters(valores[, valor_dito]) | Atribuir parâmetros numéricos a valores que resultam em um novo circuito. |
| block_until_ready() | Bloqueia a execução do código até que o circuito esteja pronto (disponível após a execução em um backend). |
| c_if(creg,valor) | Aplica uma condição clássica para a aplicação de uma instrução controlada. |
| cast(valor, _tipo) | Melhor esforço para converter valor para tipo. |
| cbit_argument_conversion(clbit_representation) | Converte várias representações clássicas de bits (como índices, intervalo, etc.) em uma lista de bits clássicos. |
| ccx(control_qubit1, control_qubit2, target_qubit) | Aplicar CCXGate. |
| ch(control_qubit, target_qubit[, rótulo, …]) | Aplicar CHGate. |
| cls_instances() | Retorna o número atual de instâncias desta classe, útil para nomeação automática. |
| cls_prefix() | Retorne o prefixo a ser usado para nomeação automática. |
| cnot(control_qubit, target_qubit[, rótulo, …]) | Aplicar CXGate. |
| combine(rrs) | DEPRECATED - Retorna rhs anexado a self se self contiver registradores compatíveis. |
| compiled_circuit_qasm | O código QASM do circuito compilado (disponível após a execução em um backend). |
| compiled_circuit_dag | O DAG (Directed Acyclic Graph) do circuito compilado (disponível após a execução em um backend). |
| compose(outro[, qubits, clbits, frontal, local]) | Compor circuito com outro circuito ou instrução, , agindo nos qubits especificados e opcionalmente permutando fios. |
| control([num_ctrl_qubits, rótulo, ctrl_state]) | Controle este circuito em num_ctrl_qubitsqubits. |
| copy([nome]) | Copie o circuito. |
| count_ops() | Conte cada tipo de operação no circuito. |
| cp(theta, control_qubit, target_qubit[, …]) | Aplicar CPhaseGate. |
| crx(theta, control_qubit, target_qubit[, …]) | Aplicar CRXGate. |
| cry(theta, control_qubit, target_qubit[, …]) | Aplicar CRYGate. |
| crz(theta, control_qubit, target_qubit[, …]) | Aplicar CRZGate. |
| cswap(control_qubit, target_qubit1, …[, …]) | Aplicar CSwapGate. |
| csx(control_qubit, target_qubit[, rótulo, …]) | Aplicar CSXGate. |
| cu(teta, phi, lam, gama, control_qubit, …) | Aplicar CUGate. |
| cu1(theta, control_qubit, target_qubit[, …]) | Aplicar CU1Gate. |
| cu3(theta, phi, lam, control_qubit, target_qubit) | Aplicar CU3Gate. |
| cx(control_qubit, target_qubit[, rótulo, …]) | Aplicar CXGate. |
| cy(control_qubit, target_qubit[, rótulo, …]) | Aplicar CYGate. |
| cz(control_qubit, target_qubit[, rótulo, …]) | Aplicar CZGate. |
| dcx(qubit1, qbit2) | Aplicar DCXGate. |
| decompose() | Decompor o circuito um nível (decomposição rasa), em uma sequência de portas elementares (disponível após a execução em um backend). |
| delay(duração [, qrg, unidade]) | Aplicar Delay. |
| depth() | Profundidade do circuito de retorno, ou seja, número de camadas de portas (comprimento do caminho crítico). |
| diagonal(diag, qubit) | Anexar uma porta diagonal a um circuito. |
| draw([saída, escala, nome do arquivo, estilo, …]) | Desenhar a representação visual do circuito quântico. |
| ecr(qubit1, qbit2) | Aplicar ECRGate. |
| extend(rrs) | OBSOLETO - Acrescente QuantumCircuit ao RHS se ele contiver registradores compatíveis. |
| fredkin(control_qubit, target_qubit1, …) | Aplicar CSwapGate. |
| from_qasm_file(caminho) | Gerar um objeto QuantumCircuit a partir de um arquivo QASM. |
| from_qasm_str(qasm_str) | Pegue uma string QASM e gere um objeto QuantumCircuit . |
| h(qubit) | Aplicar HGate. |
| hamiltonian(operador, tempo, qubits [, rótulo]) | Aplique a evolução hamiltoniana aos qubits. |
| has_register(registro) | Teste se este circuito possui o registrador r. |
| i(qubit) | Aplicar IGate. |
| id(qubit) | Aplicar IGate. |
| initialize(params [, qubits]) | Inicialize qubits em um estado específico. |
| inverse() | Inverter (tirar adjunto) deste circuito. |
| iso(isometria, q_input, q_ancillas_for_output) | Anexe uma isometria arbitrária de m a n qubits a um circuito. |
| isometry(isometria, q_input, …[, …]) | Anexe uma isometria arbitrária de m a n qubits a um circuito. |
| iswap(qubit1, qbit2) | Aplicar iSwapGate. |
| is_parameterized() | Indica se o circuito possui parâmetros. |
| mcp(lam, control_qubits, target_qubit) | Aplicar MCPhaseGate. |
| mcrx(theta, q_controls, q_target[, …]) | Aplicar porta de rotação X com controle múltiplo |
| mcry(theta, q_controls, q_target[, …]) | Aplicar porta de rotação Y controlada por múltiplos |
| mcrz(lam, q_controls, q_target[, …]) | Aplicar porta de rotação Z com controle múltiplo |
| mct(control_qubits, target_qubit[, …]) | Aplicar MCXGate. |
| mcu1(lam, control_qubits, target_qubit) | Aplicar MCU1Gate. |
| mcx(control_qubits, target_qubit[, …]) | Aplicar MCXGate. |
| measure(qubit, cbit) | Medir bit quântico em bit clássico (tuplas). |
| measure_active([no lugar]) | Adiciona medição a todos os qubits não ociosos. |
| measure_all([no lugar]) | Adiciona medição a todos os qubits. |
| ms(theta, qubits) | Aplicar MSGate. |
| num_connected_components([unitário_somente]) | Para quantos subcircuitos não emaranhados o circuito pode ser fatorado. |
| num_nonlocal_gates() | Número de retorno de portas não locais (ou seja, |
| num_tensor_factors() | Calcula o número de fatores tensores apenas na parte unitária (quântica) do circuito. |
| num_unitary_factors() | Calcula o número de fatores tensores apenas na parte unitária (quântica) do circuito. |
| p(teta, qubit) | Aplicar PhaseGate. |
| pauli(pauli_string, qubits) | Aplicar PauliGate. |
| power(potência [, matriz_potência]) | Eleve este circuito à potência de power. |
| qasm([formatado, nome do arquivo]) | Retorna a string OpenQASM. |
| qbit_argument_conversion(representação_qubit) | Converte várias representações de qubits (como índices, intervalo, etc.) em uma lista de qubits. |
| qubit_duration(*qubits) | Retorna a duração entre o horário de início e término da primeira e da última instrução, excluindo atrasos, sobre os qubits fornecidos. |
| qubit_start_time(*qubits) | Retorne a hora de início da primeira instrução, excluindo atrasos, sobre os qubits fornecidos. |
| qubit_stop_time(*qubits) | Retorna o tempo de parada da última instrução, excluindo atrasos, sobre os qubits fornecidos. |
| r(theta, phi, qubit) | Aplicar RGate. |
| rcccx(control_qubit1, control_qubit2, …) | Aplicar RC3XGate. |
| rccx(control_qubit1, control_qubit2, …)remove_final_measurements([no lugar]) | Aplicar RCCXGate.Remove a medição final em todos os qubits, se estiverem presentes. |
| remove_final_measurements | Remove todas as instruções de medição finais do circuito. |
| repeat(repetições) | Repita este circuito repsvezes. |
| reset(qubit) | Reiniciar o qubit. |
| reverse_bits() | Inverte a ordem dos bits clássicos associados aos qubits do circuito. |
| reverse_ops() | Inverta o circuito invertendo a ordem das instruções. |
| rv(vx, vy, vz, qubit) | Aplicar RVGate. |
| rx(teta, qubit[, rótulo]) | Aplicar RXGate. |
| rxx(teta, qubit1, qubit2) | Aplicar RXXGate. |
| ry(teta, qubit[, rótulo]) | Aplicar RYGate. |
| ryy(teta, qubit1, qubit2) | Aplicar RYYGate. |
| rz(fi, onde) | Aplicar RZGate. |
| rzx(teta, qubit1, qubit2) | Aplicar RZXGate. |
| rzz(teta, qubit1, qubit2) | Aplicar RZZGate. |
| s(qubit) | Aplicar SGate. |
| save_amplitudes(params[, label, pershot, …]) | Salve amplitudes complexas de vetores de estado. |
| save_amplitudes_squared(parâmetros[, rótulo, …]) | Salve as amplitudes do vetor de estado ao quadrado (probabilidades). |
| save_density_matrix([qubits, rótulo, …]) | Salve o estado quântico atual do simulador como uma matriz de densidade. |
| save_expectation_value(operador, qubits[, …]) | Salve o valor esperado de um operador hermitiano. |
| save_expectation_value_variance(operador, qubits) | Salve o valor esperado de um operador hermitiano. |
| save_matrix_product_state([rótulo, pershot, …]) | Salve o estado quântico atual do simulador como um estado de produto de matriz. |
| save_probabilities([qubits, rótulo, …]) | Salve o vetor de probabilidades do resultado da medição. |
| save_probabilities_dict([qubits, rótulo, …]) | Salve o vetor de probabilidades do resultado da medição. |
| save_stabilizer([rótulo, pershot, condicional]) | Salve o estado quântico do simulador do estabilizador atual como um Clifford. |
| save_state([rótulo, pershot, condicional]) | Salve o estado quântico atual do simulador. |
| save_statevector([rótulo, pershot, condicional]) | Salve o estado quântico atual do simulador como um vetor de estado. |
| save_statevector_dict([rótulo, pershot, …]) | Salve o estado quântico do simulador atual como um vetor de estado como um dict. |
| save_superop([rótulo, pershot]) | Salve o estado atual do simulador superop. |
| save_unitary([rótulo, pershot]) | Salve o estado atual do simulador unitário. |
| sdg(qubit) | Aplicar SdgGate. |
| set_density_matrix(estado) | Defina o estado da matriz de densidade do simulador. |
| set_matrix_product_state(estado) | Defina o estado do produto da matriz do simulador. |
| set_stabilizer(estado) | Defina o estado do estabilizador Clifford do simulador. |
| set_statevector(estado) | Defina o estado do vetor de estado do simulador. |
| set_superop(estado) | Defina o estado superop do simulador. |
| set_unitary(estado) | Defina o estado do simulador. |
| size() | Retorna o número total de operações de portão no circuito. |
| snapshot(label[, snapshot_type, qubits, params]) | Faça um instantâneo do vetor de estado da representação interna do simulador. |
| snapshot_density_matrix(rótulo [, qubits]) | Faça um instantâneo da matriz de densidade do estado do simulador. |
| snapshot_expectation_value(rótulo, op, qubits) |
Faça um instantâneo do valor esperado |
| snapshot_probabilities(rótulo, qubits [, variância]) | Faça um instantâneo de probabilidade do estado do simulador. |
| snapshot_stabilizer(rótulo) | Tire um instantâneo do estabilizador do estado do simulador. |
| snapshot_statevector(rótulo) | Faça um instantâneo do vetor de estado do estado do simulador. |
| squ(matriz_unitária, qubit[, modo, …])swap(qubit1, qbit2) | Decomponha um arbitrário 2*2 unitário em três portas de rotação.Aplicar SwapGate. |
| sx(qubit) | Aplicar SXGate. |
| sxdg(qubit) | Aplicar SXdgGate. |
| t(qubit) | Aplicar TGate. |
| tdg(qubit) | Aplicar TdgGate. |
| tensor(outro [, local]) | tensor selfcom other. |
| to_gate([parameter_map, label]) | Criar uma porta fora deste circuito. |
| to_instruction([mapa_parâmetro]) | Criar uma instrução fora deste circuito. |
| toffoli(control_qubit1, control_qubit2, …) | Aplicar CCXGate. |
| u(theta, phi, lam, qubit) | Aplicar UGate. |
| u1(teta, qubit) | Aplicar U1Gate. |
| u2(phi, azul, qubit) | Aplicar U2Gate. |
| u3(theta, phi, lam, qubit) | Aplicar U3Gate. |
| uc(gate_list, q_controls, q_target[, …]) | Conecte portas uniformemente controladas (também chamadas de portas multiplexadas) a um circuito. |
| ucrx(angle_list, q_controls, q_target) | Conecte uma porta de rotação Rx uniformemente controlada (também chamada de multiplexada) a um circuito. |
| ucry(angle_list, q_controls, q_target) | Conecte uma porta de rotação Ry uniformemente controlada (também chamada de multiplexada) a um circuito. |
| ucrz(angle_list, q_controls, q_target) | Conecte uma porta de rotação Rz uniformemente controlada (também chamada de portas multiplexadas) a um circuito. |
| unitary(obj, qubits[, rótulo]) | Retornar a representação matricial unitária do circuito. |
| validate() | Verifica se o circuito é válido, detectando erros comuns. |
| width() | Retorna o número de qubits mais clbits no circuito. |
| x(qubit[, rótulo]) | Aplicar XGate. |
| y(qubit) | Aplicar YGate. |
| z(qubit) | Aplicar ZGate. |
Atributos da classe QuantumCircuit
A Tabela 2 contém atribuitos da classe QuantumCircuit.
| Nome | Nota |
|---|---|
| circuit_arguments | Os argumentos do circuito, se houver. |
| circuit_parameters | Os parâmetros do circuito, se houver. |
| clbits | Obtém a lista de bits clássicos na ordem em que os registradores foram adicionados. |
| data | Obtém uma lista das operações (por exemplo, portas, barreiras e operações de medição) no circuito. |
| duration | A duração estimada da execução do circuito (disponível após a execução em um backend). |
| global_phase | A fase global do circuito em radianos. |
| metadata | Metadados associados ao circuito. |
| name | Nome do circuito. |
| num_qubits | Número de qubits do circuito. |
| num_clbits | Número de bits clássicos do circuito. |
| parameters | Parâmetros do circuito, se houver. |
| qargs | Qubits afetados pelas instruções do circuito. |
| qubits | Lista de qubits na ordem em que os registradores foram adicionados |
| regs | Registradores de qubits e bits clássicos do circuito. |
| cargs | Os bits clássicos afetados pelas instruções do circuito. |
Portas da classe QuantumCircuit
A Tabela 3 contém métodos comumente usados para operar portas de qubit único da classe QuantumCircuit, com exemplos usando a variável qc.
Tabela 3 - Portas de qubit único
| Nome | Exemplo | Nota |
|---|---|---|
| H, Hadamard | qc.h(0) | Aplica porta H ao qubit 0. |
| I, identidade | qc.id(2) ou qc.i(2) | Aplica a porta I ao qubit 2. |
| P, Fase | qc.p(math.pi/2,0) | Aplica porta P com rotação de fase π /2 para qubit 0. |
| RX | qc.rx(math.pi/4,2) | Aplica porta RX com rotação π/4 ao qubit 2. |
| RY | qc.ry(math.pi/8,0) | Aplica RY gate com rotação π/8 ao qubit 0. |
| RZ | qc.rz(math.pi/2,1) | Aplica porta RZ com rotação π/2 ao qubit 1. |
| S | qc.s(3) | Aplica a porta S ao qubit 3. Equivalente à porta P com rotação de π/2 fases. |
| SDG | qc.sdg(3) | Aplica a porta S ao qubit 3. Equivalente à porta P com rotação de 3π/2 fases. |
| SX | qc.sx(2) | Aplica a porta SX (raiz quadrada de X) ao qubit 2. Equivalente à porta RX com rotação π/2. |
| T | qc.t(1) | Aplica a porta T ao qubit 1. Equivalente à porta P com rotação de π/4 fases. |
| TDG | qc.tdg(1) | Aplica a porta T ao qubit 1. Equivalente à porta P com rotação de 7π/4 fases. |
| U | qc.u(math.pi/2, 0, math.pi, 1) | Aplica rotação com 3 ângulos de Euler ao qubit 1. |
| X | qc.x(3) | Aplica a porta X ao qubit 3. |
| Y | qc.y([0,2,3]) | Aplica a porta Y aos qubits 0, 2 e 3. |
| Z | qc.z(2) | Aplica a porta Z ao qubit 2. Equivalente à porta P com rotação de fase π. |
Desenho ilustrativo de um circuito sem sentido, com exemplos das portas de qubit único da tabela:
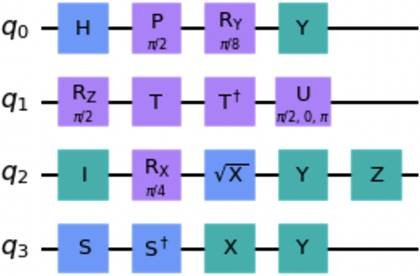
A Tabela 4 contém os métodos comumente usados de portas multiqubit.
Tabela 4 – Portas multiqubit
| Nome | Exemplo | Nota |
|---|---|---|
| CCX Toffoli | qc.ccx(0,1,2) | Aplica a porta X ao fio quântico 2, sujeito ao estado dos qubits de controle nos fios 0 e 1. |
| CH | qc.ch(0,1) | Aplica a porta H ao fio quântico 1, sujeito ao estado do qubit de controle no fio 0 |
| CP Fase de Controle | qc.cp(math.pi/4, 0, 1) | Aplica a porta de fase ao fio quântico 1, sujeito ao estado do qubit de controle no fio 0. |
| CRX Control-RX | qc.crx(math.pi/2, 2, 3) | Aplica a porta RX ao fio quântico 3, sujeito ao estado do qubit de controle no fio 2. |
| CRY Control-RY | qc.cry(math.pi/8, 2, 3) | Aplica a porta RY ao fio quântico 3, sujeito ao estado do qubit de controle no fio 2. |
| CRZ Control-RZ | qc.crz(math.pi/4, 0, 1) | Aplica a porta RZ ao fio quântico 1, sujeito ao estado do qubit de controle no fio 0. |
| CSwap, Fredkin | qc.cswap(0, 2, 3) ou qc.fredkin(0, 2, 3) | Troca os estados de qubit dos fios 2 e 3, sujeitos ao estado do qubit de controle no fio 0. |
| CSX | qc.csx(0,1) | Aplica a porta SX (raiz quadrada de X) ao fio quântico 1, sujeito ao estado do qubit de controle no fio 0. |
| CU | qc.cu(math.pi/2, 0, math.pi, 0, 0, 1) | Aplica a porta U com argumento de fase global adicional ao fio quântico 1, sujeito ao estado do qubit de controle no fio 0. |
| CX, CNOT | qc.cx(2,3) ou qc.cnot(2,3) | Aplica a porta X ao fio quântico 3, sujeito ao estado do qubit de controle no fio 2. |
| CY, Controle-Y | qc.cy(2,3) | Aplica a porta Y ao fio quântico 3, sujeito ao estado do qubit de controle no fio 2 |
| CZ, Control-Z | qc.cz(1,2) | Aplica a porta Z ao fio quântico 2, sujeito ao estado do qubit de controle no fio 1. |
| DCX | qc.dcx(2,3) | Aplica duas portas CNOT cujos qubits de controle estão nos fios 2 e 3. |
| iSwap | qc.iswap(0,1) | Troca os estados de qubit dos fios 0 e 1 e muda a fase do |01⟩ e |10⟩ amplitudes de i |
| MCP, fase de controle múltiplo | qc.mcp(math.pi/4, [0,1,2], 3) | Aplica a porta de fase ao fio quântico 3, sujeito ao estado dos qubits de controle nos fios 0, 1 e 2. |
| MCX, Multicontrole X | qc.mcx([0,1,2], 3) | Aplica a porta X ao fio quântico 3, sujeito ao estado dos qubits de controle nos fios 0, 1 e 2. |
| swap | qc.swap(2, 3) | Troca os estados de qubit dos fios 2 e 3. |
Desenho de circuito sem sentido com exemplos de portas multiqubit da tabela:
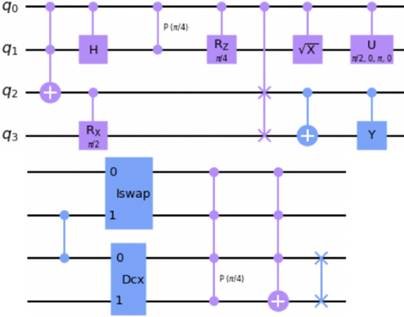
Desenhando um circuito quântico
O método draw() desenha um circuito quântico em vários formatos. O trecho de código a seguir usa o método draw() com formato padrão:
qc = QuantumCircuit(3)
qc.h(0)
qc.cx(0, 1)
qc.cx(0, 2)
qc.draw()Desenho do circuito usando o método draw():
┌───┐
q_0: ┤ H ├──■────■──
└───┘┌─┴─┐ │
q_1: ─────┤ X ├──┼──
└───┘┌─┴─┐
q_2: ──────────┤ X ├
└───┘Criando uma barreira no circuito quântico
O método barrier() coloca uma barreira em um circuito quântico, fornecendo a separação funcional entre portas nos fios. As portas de ambos os lados de uma barreira não são candidatos a serem otimizados juntos, pois o circuito é convertido para rodar em hardware quântico ou em um simulador.
O conjunto de portas usando o Qiskit representa uma abstração para as portas reais implementadas em um determinado computador ou simulador quântico. O Qiskit transcompila as portas para aquelas implementados na plataforma de destino, combinando as portas sempre que possível, visando otimizar o circuito.
Método barrier()
O método barrier() assume como argumento opcional os fios de qubits nos quais a barreira deve ser colocada. Se nenhum argumento for fornecido, a barreira será colocada em todos os fios quânticos. Este método cria uma instância da classe.
O código a seguir demonstra o uso do método barrier() com e sem argumentos:
qc = QuantumCircuit(2)
qc.h([0,1])
qc.barrier()
qc.x(0)
qc.x(0)
qc.s(1)
qc.barrier([1])
qc.s(1)
qc.draw()Desenho do circuito usando o método barrier():
┌───┐ ░ ┌───┐┌───┐
q_0: ┤ H ├─░─┤ X ├┤ X ├─────
├───┤ ░ ├───┤└─░─┘┌───┐
q_1: ┤ H ├─░─┤ S ├──░──┤ S ├
└───┘ ░ └───┘ ░ └───┘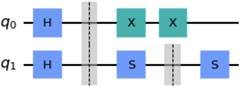
Observe que as portas S no circuito são separadas por uma barreira e, portanto, não são candidatas a serem combinadas em uma porta Z. No entanto, as portas X podem ser combinadas removendo ambas, pois elas cancelam uma a outra para fora.
Medindo o circuito quântico
Os métodos comumente usados para medir circuitos quânticos são measure() e measure_all(). O primeiro é útil quando o circuito quântico contém fios clássicos nos quais receber o resultado de uma medição. O último é útil quando o circuito quântico não possui fios clássicos. Esses métodos criam instâncias da classe Measure.
Método measure()
O método measure() tem dois argumentos: os fios qubit a serem medidos e os fios clássicos nos quais armazenar os bits resultantes. O código a seguir usa measure():
qc = QuantumCircuit(3, 3)
qc.h([0,1,2])
qc.measure([0,1,2],[0,1,2])
qc.draw()Desenho do circuito usando o método measure():
┌───┐┌─┐
q_0: ┤ H ├┤M├──────
├───┤└╥┘┌─┐
q_1: ┤ H ├─╫─┤M├───
├───┤ ║ └╥┘┌─┐
q_2: ┤ H ├─╫──╫─┤M├
└───┘ ║ ║ └╥┘
c: 3/══════╩══╩══╩═
0 1 2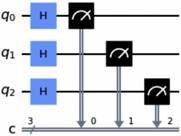
O método measure() anexou as operações de medição solicitadas ao circuito.
Método measure_all()
O método measure_all() pode ser chamado com ou sem argumentos.
qc = QuantumCircuit(3)
qc.h([0,1,2])
qc.measure_all()
qc.draw()Desenho do circuito resultante da chamada de measure_all():
┌───┐ ░ ┌─┐
q_0: ┤ H ├─░─┤M├──────
├───┤ ░ └╥┘┌─┐
q_1: ┤ H ├─░──╫─┤M├───
├───┤ ░ ║ └╥┘┌─┐
q_2: ┤ H ├─░──╫──╫─┤M├
└───┘ ░ ║ ║ └╥┘
meas: 3/═════════╩══╩══╩═
0 1 2 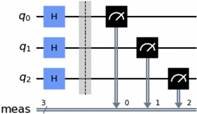
Observe que foram criados três fios clássicos e adicionada uma barreira ao circuito antes da anexação da medição.
Obtendo informações sobre um circuito quântico
Métodos comumente usados para obtenção de informações sobre um circuito quântico incluem depth(), size(), width().
Método depth()
O método depth() retorna o número de camadas (profundidade) do circuito quântico.
from qiskit import QuantumCircuit
# Cria um circuito quântico com 3 <i>qubits</i> e 2 portas quânticas
qc = QuantumCircuit(3)
qc.h(0)
qc.cx(0, 1)
qc.cx(1, 2)
qc.x(2)
# Imprime a profundidade do circuito
print("Profundidade do circuito:", qc.depth())Neste exemplo, criamos um circuito quântico com 3 qubits e aplicamos algumas portas quânticas: uma porta Hadamard (H) no primeiro qubit, seguido por duas portas CNOT (cx) para criar um emaranhamento entre os qubits 0, 1 e 2, e finalmente uma porta X no terceiro qubit. Em seguida, usamos o método depth() para obter a profundidade do circuito e imprimimos o resultado.
Profundidade do circuito: 4Método size()
O método size() retorna o número total de qubits no circuito.
from qiskit import QuantumCircuit
# Cria um circuito quântico com 4 <i>qubits</i>
qc = QuantumCircuit(4)
# Adiciona algumas portas quânticas ao circuito
qc.h(0)
qc.cx(0, 2)
qc.cx(1, 3)
# Imprime o tamanho do circuito (número de <i>qubits</i>)
print("Tamanho do circuito:", qc.size())Neste exemplo, criamos um circuito quântico com 4 qubits usando a classe QuantumCircuit(4). Em seguida, aplicamos algumas portas quânticas: uma porta Hadamard (H) no primeiro qubit e duas portas CNOT (cx) entre os qubits 0 e 2, e entre os qubits 1 e 3. Por fim, usamos o método size() para obter o tamanho do circuito, ou seja, o número total de qubits presentes no circuito, e imprimimos o resultado.
Tamanho do circuito: 3Método width()
O método width() retorna o número máximo de qubits ativos em um determinado momento durante a execução do circuito.
from qiskit import QuantumCircuit
# Cria um circuito quântico com 3 <i>qubits</i>
qc = QuantumCircuit(3)
# Adiciona algumas portas quânticas ao circuito
qc.h(0)
qc.cx(0, 1)
qc.cx(1, 2)
# Imprime a largura do circuito (número máximo de <i>qubits</i> ativos)
print("Largura do circuito:", qc.width())Neste exemplo, criamos um circuito quântico com 3 qubits usando a classe QuantumCircuit(3). Em seguida, aplicamos algumas portas quânticas: uma porta Hadamard (H) no primeiro qubit e duas portas CNOT (cx) para criar um emaranhamento entre os qubits 0, 1 e 2. Finalmente, usamos o método width() para obter a largura do circuito, ou seja, o número máximo de qubits ativos em qualquer ponto durante a execução do circuito, e imprimimos o resultado.
Largura do circuito: 3Os atributos comumente usados para obter informações sobre um circuito quântico incluem clbits, data, global_phase, num_clbits, num_qubits e qubits, apresentados na Tabela 2 - Atributos da classe QuantumCircuit.
Manipulando um circuito quântico
Os principais métodos para manipular os circuitos quânticos são: append(), bind_parameters(), compose(), copy(), decompose(), initialize(), reset(), to_gate() e to_instruction().
Método append()
O método append() anexa uma instrução ou porta ao final do circuito em fios especificados, modificando o circuito no local. O código abaixo anexa uma porta da classe CXGate, do pacote qiskit.circuit.library.
from qiskit.circuit.library import CXGate
qc = QuantumCircuit(2)
qc.h(1)
cx_gate = CXGate()
qc.append(cx_gate, [1,0])
qc.draw()Desenho do circuito resultante do método append():
┌───┐
q_0: ─────┤ X ├
┌───┐└─┬─┘
q_1: ┤ H ├──■──
└───┘ Método bind_parameters()
O método bind_parameters() vincula parâmetros a um circuito quântico.
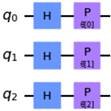
O trecho de código a seguir cria um circuito no qual existem três portas de fase parametrizadas. Observe que os argumentos para os construtores da classe Parameter neste trecho de código utilizam textos compostos pelo caracter theta seguido de ponto e algarismo, na declaração dos parâmetro do circuito quântico.
from qiskit.circuit import QuantumCircuit, Parameter
theta1 = Parameter('θ¸1')
theta2 = Parameter('θ¸2')
theta3 = Parameter('θ¸3')
qc = QuantumCircuit(3)
qc.h([0,1,2])
qc.p(theta1,0)
qc.p(theta2,1)
qc.p(theta3,2)
qc.draw()Desenho do circuito parametrizado:
┌───┐┌────────┐
q_0: ┤ H ├┤ P(θ¸1) ├
├───┤├────────┤
q_1: ┤ H ├┤ P(θ¸2) ├
├───┤├────────┤
q_2: ┤ H ├┤ P(θ¸3) ├
└───┘└────────┘Para vincular os valores dos parâmetros a um novo circuito, podemos passar ao método bind_parameters() um dicionário que contém as referências aos parâmetros desejados e seus respectivos valores. O trecho de código a seguir usa essa técnica no qual o circuito é limitado por valores substituídos nos parâmetros da porta de fase:
from qiskit.circuit import QuantumCircuit
import math
b_qc = qc.bind_parameters({
theta1: math.pi/8,
theta2: math.pi/4,
theta3: math.pi/2})
b_qc.draw()Desenho do circuito vinculado com os valores de rotação da porta de fase:
┌───┐┌────────┐
q_0: ┤ H ├┤ P(π/8) ├
├───┤├────────┤
q_1: ┤ H ├┤ P(π/4) ├
├───┤├────────┤
q_2: ┤ H ├┤ P(π/2) ├
└───┘└────────┘Método compose()
O método compose() retorna um novo circuito composto pelo original e um outro:
qc = QuantumCircuit(2,2)
qc.h(0)
another_qc = QuantumCircuit(2,2)
another_qc.cx(0,1)
bell_qc = qc.compose(another_qc)
bell_qc.draw()Desenho do circuito resultante do método compose():
┌───┐
q_0: ┤ H ├──■──
└───┘┌─┴─┐
q_1: ─────┤ X ├
└───┘
c: 2/══════════Observe que um circuito passado para o método compose() pode ter menos fios quânticos ou clássicos do que o circuito original.
Método copy()
O método copy() retorna uma cópia do circuito original:
qc = QuantumCircuit(3)
qc.h([0,1,2])
new_qc = qc.copy()Método decompose()
O método decompose() retorna um novo circuito depois de decompor o circuito original em um nível:
qc = QuantumCircuit(2)
qc.h(0)
qc.s(0)
qc.x(1)
decomposed_qc = qc.decompose()
decomposed_qc.draw()Desenho do circuito resultante do método decompose(), no qual as portas S, H e X são decompostas nas operações mais fundamentais da porta U:
┌─────────┐ ┌─────────┐
q_0: ─┤ U2(0,π) ├─┤ U1(π/2) ├
┌┴─────────┴┐└─────────┘
q_1: ┤ U3(π,0,π) ├───────────
└───────────┘ 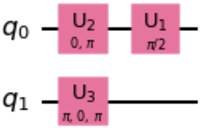
Método initialize()
O método initialize() inicializa qubits de um circuito quântico para um determinado estado. Não é uma operação unitária.
O código a seguir usa o método initialize() com o circuito sendo inicializado para o vetor de estado normalizado |11⟩:
qc = QuantumCircuit(2)
qc.initialize([0, 0, 0, 1])
qc.draw()Desenho do circuito resultante do método initialize():
┌──────────────────────┐
q_0: ┤0 ├
│ Initialize(0,0,0,1) │
q_1: ┤1 ├
└──────────────────────┘
Método reset()
O método reset() redefine um qubit em um circuito quântico para o estado |0⟩ e não é uma operação unitária.
qc = QuantumCircuit(1)
qc.x(0)
qc.reset(0)
qc.draw()Desenho do circuito resultante do método reset():
┌───┐
q: ┤ X ├─|0>─
└───┘ Observe que o estado do qubit é |1⟩ antes da operação de reinicialização. Este método cria uma instância da classe Reset (consulte “Redefinir”).
Método to_gate()
O método to_gate() cria uma porta personalizada a partir de um circuito quântico. O código abaixo cria um circuito e o converte em uma porta:
anti_cnot_qc = QuantumCircuit(2)
anti_cnot_qc.x(0)
anti_cnot_qc.cx(0,1)
anti_cnot_qc.x(0)
anti_cnot_qc.draw()Desenho do circuito:
┌───┐ ┌───┐
q_0: ┤ X ├──■──┤ X ├
└───┘┌─┴─┐└───┘
q_1: ─────┤ X ├─────
└───┘ Esta porta personalizado implementará uma porta NOT anticontrole no qual a porta X é aplicado somente quando o qubit de controle é |0⟩.
O trecho de código a seguir cria um circuito que usa essa porta personalizada:
anti_cnot_gate = anti_cnot_qc.to_gate()
qc = QuantumCircuit(3)
qc.x([0,1,2])
qc.append(anti_cnot_gate, [0,2])
qc.decompose().draw()Desenho decomposto desse circuito com o método to_gate():
┌───────────┐┌───┐ ┌───┐
q_0: ┤ U3(π,0,π) ├┤ X ├──■──┤ X ├
├───────────┤└───┘ │ └───┘
q_1: ┤ U3(π,0,π) ├───────┼───────
├───────────┤ ┌─┴─┐
q_2: ┤ U3(π,0,π) ├─────┤ X ├─────
└───────────┘ └───┘
Observação: Uma porta representa uma operação unitária. Para criar uma operação personalizada que não seja unitária, use o método to_instruction().
Método to_instruction()
O método to_instruction() cria uma instrução de um circuito quântico.
O trecho de código a seguir cria um circuito que será convertido em uma instrução:
qc = QuantumCircuit(1)
qc.reset(0)
qc.x(0)
qc.draw()Desenho do circuito que será convertido em uma instrução:
┌───┐
q: ─|0>─┤ X ├
└───┘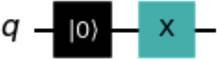
A instrução personalizada a seguir redefinirá um qubit e aplicará uma porta X, redefinindo o qubit para o estado |1⟩. O trecho de código a seguir cria um circuito que usa essa instrução personalizada:
inst = qc.to_instruction()
qc = QuantumCircuit(2)
qc.h([0,1])
qc.reset(0)
qc.append(inst,[1])
qc.decompose().draw()Desenho decomposto do circuito da instrução criada pelo método to_instruction():
┌───┐
q: ─|0>─┤ X ├
└───┘
Observação: uma instrução representa uma operação que não é necessariamente unitária. Para criar uma operação customizada unitária, use o método to_gate().
QASM
O Qiskit é uma biblioteca poderosa e abrangente para computação quântica em Python, oferecendo várias funcionalidades para construção, simulação e execução de circuitos quânticos. Uma dessas funcionalidades é a capacidade de trabalhar com código QASM (Quantum Assembly Language) por meio dos métodos qasm(), from_qasm_str() e from_qasm_file() da classe QuantumCircuit.
O QASM é uma linguagem de montagem para descrever circuitos quânticos de forma textual e fornece uma representação mais legível dos circuitos, permitindo a construção precisa de circuitos personalizados. O Qiskit permite a integração perfeita do QASM em seus fluxos de trabalho por meio dos métodos mencionados.
O método qasm() é usado para obter a representação QASM de um circuito quântico. Ele retorna uma string contendo o código QASM correspondente ao circuito. Isso é particularmente útil quando você precisa compartilhar ou salvar o circuito em um formato legível por humanos ou quando deseja integrar o circuito com outras ferramentas ou linguagens que suportam QASM.
Por outro lado, os métodos from_qasm_str() e from_qasm_file() são usados para criar um objeto da classe QuantumCircuit a partir de um código QASM. O método from_qasm_str() permite fornecer diretamente um texto contendo o código QASM, e o método from_qasm_file() permite ler o código QASM de um arquivo especificado.
Esses métodos são úteis quando você precisa importar circuitos existentes em QASM para o Qiskit ou quando deseja trabalhar com circuitos definidos externamente em QASM. Eles simplificam o processo de conversão de circuitos QASM em objetos QuantumCircuit manipuláveis dentro do Qiskit, permitindo que você aproveite todos os recursos e funcionalidades oferecidos pelo Qiskit para simulação, execução e análise de circuitos quânticos.
Os métodos qasm(), from_qasm_str() e from_qasm_file() do Qiskit fornecem uma maneira conveniente de trabalhar com código QASM em seus projetos de computação quântica, permitindo que você obtenha a representação QASM de um circuito, bem como importe circuitos definidos em QASM para o Qiskit. Esses recursos aprimoram a interoperabilidade e a flexibilidade do Qiskit, permitindo a integração de circuitos QASM em fluxos de trabalho de maneira eficiente e eficaz.
Método qasm()
O método qasm() retorna um programa da linguagem OpenQASM que representa o circuito quântico. O código a seguir utiliza o método qasm() retornando o script da linguagem OpenQASM resultante.
qc = QuantumCircuit(2, 2)
qc.h(0)
qc.cx(0, 1)
qasm_str = qc.qasm()
print(qasm_str)Programa OpenQASM:
OPENQASM 2.0;
include "qelib1.inc";
qreg q[2];
creg c[2];
h q[0];
cx q[0],q[1];Método from_qasm_str()
O método from_qasm_str() retorna um novo circuito de um texto contendo um programa com instruções QASM:
qasm_str = """
OPENQASM 2.0;
include "qelib1.inc";
qreg q[2];
creg c[2];
h q[0];
cx q[0],q[1];
measure q[0] -> c[0];
measure q[1] -> c[1];
"""
new_qc = QuantumCircuit.from_qasm_str(qasm_str)
new_qc.draw()Desenho do circuito resultante:
┌───┐ ┌─┐
q_0: ┤ H ├──■──┤M├───
└───┘┌─┴─┐└╥┘┌─┐
q_1: ─────┤ X ├─╫─┤M├
└───┘ ║ └╥┘
c: 2/═══════════╩══╩═
0 1 Método from_qasm_file()
O método from_qasm_file() retorna um novo circuito a partir de um arquivo contendo um programa de linguagem de montagem quântica em QASM. O trecho de código a seguir usa o método from_qasm_file():
new_qc = QuantumCircuit.from_qasm_file("file.qasm")Salvando o estado ao executar um circuito no AerSimulator
Ao executar um circuito em um AerSimulator backend (AerSB), o estado do simulador pode ser salvo na instância do circuito usando os métodos QuantumCircuit da Tabela 5 - Métodos para salvar o estado do simulador. Observe que esses métodos estão disponíveis após a obtenção de um AerSB.
Tabela 5 - Métodos para salvar o estado do simulador
| Nome do método | Descrição |
|---|---|
| save_state | Salva o estado do simulador conforme apropriado para o método de simulação. |
| save_density_matrix | Salva o estado do simulador como uma matriz de densidade. |
| save_matrix_product_state | Salva o estado do simulador como um tensor de estado do produto da matriz. |
| save_stabilizer | Salva o estado do simulador como um estabilizador Clifford. |
| save_statevector | Salva o estado do simulador como um vetor de estado. |
| save_superop | Salva o estado do simulador como uma matriz de superoperador do circuito de execução. |
| save_unitary | Salva o estado do simulador como uma matriz unitária do circuito de execução. |
6.5 - Classe QuantumRegister
A classe QuantumRegister representa um registro quântico em um circuito quântico, sendo usada para definir e manipular os qubits em um circuito, que são as unidades básicas de informação quântica. Desempenha um papel fundamental na criação e construção de circuitos quânticos no Qiskit, permitindo que os usuários especifiquem o número de qubits necessários e os acessem e modifiquem de maneira conveniente. Ao criar um circuito quântico, é necessário especificar o número de qubits em uso. Isso é feito por meio da criação de um registro quântico usando a classe QuantumRegister.
Essa classe permite aos usuários definirem o número de qubits e, opcionalmente, atribuir um nome ao registro. A sintaxe para criar um registro quântico é a seguinte:
qreg = QuantumRegister(tamanho, nome)onde tamanho é o número de qubits no registro quântico e nome é um nome opcional para o registro.
Uma vez que um registro quântico é criado, ele pode ser usado para adicionar qubits a um circuito quântico e realizar operações de portas neles. Os qubits em um registro quântico são indexados de 0 a qreg.size()-1. Por exemplo, para adicionar uma porta Hadamard em um qubit específico, pode-se usar a seguinte sintaxe:
qc.h(qreg[0])onde qc é o circuito quântico e qreg[0] se refere ao primeiro qubit do registro qreg.
A classe QuantumRegister também oferece métodos convenientes para acessar, iterar e modificar os qubits em um registro quântico.
Alguns dos métodos úteis são: __getitem__(), que permite acessar um qubit específico pelo seu índice, size(), que retorna o número de qubits no registro, e __iter__(), que permite iterar sobre os qubits no registro.
Além disso, a classe QuantumRegister pode ser usada em conjunto com a classe ClassicalRegister para criar circuitos quânticos que envolvem operações quânticas e medições clássicas.
Algumas vezes é útil tratar grupos de fios quânticos ou clássicos como uma unidade. Por exemplo, os qubits de controle das portas CNOT no circuito quântico expressos no trecho de código a seguir, bem como no desenho do circuito, esperam três qubits em superposições iguais. O fio quântico adicional no circuito é usado como uma área de risco cuja saída é desconsiderada.
from qiskit import QuantumRegister, ClassicalRegister
qr = QuantumRegister(3, 'q')
scratch = QuantumRegister(1, 'scratch')
cr = ClassicalRegister(3, 'c')
qc = QuantumCircuit(qr, scratch, cr)
qc.h(qr)
qc.x(scratch)
qc.h(scratch)
qc.cx(qr[0], scratch)
qc.cx(qr[2], scratch)
qc.barrier(qr)
qc.h(qr)
qc.measure(qr, cr)
qc.draw()Desenho do circuito usando as classes QuantumRegister e ClassicalRegister:
┌───┐ ░ ┌───┐┌─┐
q_0: ┤ H ├───────■────────░─┤ H ├┤M├──────
├───┤ │ ░ ├───┤└╥┘┌─┐
q_1: ┤ H ├───────┼────────░─┤ H ├─╫─┤M├───
├───┤ │ ░ ├───┤ ║ └╥┘┌─┐
q_2: ┤ H ├───────┼────■───░─┤ H ├─╫──╫─┤M├
├───┤┌───┐┌─┴─┐┌─┴─┐ ░ └───┘ ║ ║ └╥┘
scratch: ┤ X ├┤ H ├┤ X ├┤ X ├─────────╫──╫──╫─
└───┘└───┘└───┘└───┘ ║ ║ ║
c: 3/═════════════════════════════╩══╩══╩═
0 1 2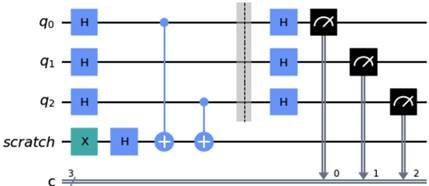
Ao definir um QuantumRegister composto por três qubits, métodos como h(), barrier() e measure() podem ser aplicados a todos os três fios passando uma referência QuantumRegister.
Da mesma forma, é possível definir um ClassicalRegister consistindo em três bits permite que o método measure() especifique todas as três ligações clássicas passando uma referência ClassicalRegister. Além disso, os nomes fornecidos aos construtores QuantumRegister e ClassicalRegister são exibidos no desenho do circuito.
Atributos da classe QuantumRegister
Os atributos da classe QuantumRegister comumente usados incluem name e size. A variável qr se refere a um objeto instanciado da classe QuantumRegister.
Tabela 6 - Atributos da classe ClassicalRegister
| Nomes | Exemplos | Notas |
|---|---|---|
| name | qr.name | Obtém o nome do registrador quântico |
| size | qr.size | Obtém o número de fios qubit no registrador quântico |
6.6 - Classe ClassicalRegister
A classe ClassicalRegister representa um registro clássico em um circuito quântico. Enquanto os registradores quânticos armazenam e manipulam informações quânticas, os registradores clássicos armazenam e processam informações clássicas resultantes das medições realizadas em um circuito quântico, desempenhando um papel fundamental na integração entre informações clássicas e quânticas em algoritmos e experimentos quânticos implementados no Qiskit.
O número de bits em um registro clássico pode ser atribuído pelo usuário, e um nome opcional. Isso é feito durante a construção do circuito quântico usando o Qiskit.
A sintaxe para criar um registro clássico é:
creg = ClassicalRegister(tamanho, nome)onde tamanho é o número de bits no registro clássico e nome é um nome opcional para o registro.
Uma vez que um registro clássico é criado, ele pode ser usado em conjunto com as operações de medição no circuito quântico para associar os resultados da medição aos bits clássicos correspondentes. Isso pode ser feito usando o método measure() do circuito, especificando o qubit a ser medido e o bit clássico associado.
Por exemplo:
qc.measure(qreg,creg)onde qreg é o registro quântico a ser medido e creg é registrador clássico em que o resultado da medição será armazenado.
A classe ClassicalRegister fornece uma maneira conveniente de lidar com os resultados das medições em um circuito quântico e permite que os usuários realizem computações clássicas adicionais com base nesses resultados. Além disso, facilita a conexão dos resultados quânticos com processos ou sistemas clássicos que podem ser usados em conjunto com os circuitos quânticos.
Atributos da classe ClassicalRegister
Os atributos da classe ClassicalRegister comumente usados incluem name e size, listados na tabela a seguir. A variável cr refere-se a um objeto ClassicalRegister.
Tabela 7 - Atributos da classe ClassicalRegister
| Nomes | Exemplos | Notas |
|---|---|---|
| name | cr.name | Obtém o nome do registrador clássico. |
| size | cr.size | Obtém o número de fios bit no registrador clássico. |
6.7 - Classe Instruction
As operações não unitárias em Qiskit, como Measure e Reset, são classes descendentes da classe Instruction.
Embora seja possível a definição de instruções personalizadas, com a criação de classes descendentes de Instruction, outra forma é usar o método to_instruction() da classe QuantumCircuit.
Métodos da classe Instruction incluem copy(), repeat() e reverse_ops(), listados na Tabela 8 - Métodos da classe Instruction. A a variável inst se refere a uma instância da classe Instruction.
Tabela 8 - Métodos da classe Instruction
| Nomes | Exemplo | Notas |
|---|---|---|
| copy | inst.copy("My inst") | Retorna uma cópia da instrução, dando o nome fornecido à cópia. |
| repeat | inst.repeat(2) | Retorna uma instrução com esta instrução repetida um determinado número de vezes. |
| reverse_ops | inst.reverse_ops() | Retorna uma instrução com suas operações na ordem inversa. |
Atributos da classe Instruction incluem definitions e params:
Tabela 9 - Atributos da classe Instruction
| nomes | Exemplo | Notas |
|---|---|---|
| definition | inst.definition | Retorna a definição em termos de portas básicas. |
| params | inst.params | Obtém os parâmetros para a instrução. |
Instruções e Portas
No Qiskit, todas as operações que podem ser aplicadas a um circuito quântico são derivadas da classe Instruction.
As operações unitárias são derivadas da classe Gate, que é uma subclasse de Instruction.
As operações unitárias controladas são derivadas da classe ControlledGate, que é uma classe descendente de Gate.
Essas classes podem ser usadas para definir novas instruções, portas unitárias e portas unitárias controladas, respectivamente.
6.8 - Classe Gate
As operações unitárias no Qiskit (como HGate e XGate) são classes descendentes de Gate.
Embora seja possível você definir suas próprias portas personalizadas subclassificando Gate, outra maneira é usar-se o método to_gate() da classe QuantumCircuit.
Métodos da classe Gate
A Tabela 10 apresenta métodos da classe Gate. A variável gate se refere a um objeto instanciado da classe Gate.
Tabela 10 - Métodos da classe Gate
| nomes | Exemplo | Notas | ||
|---|---|---|---|---|
| control | gate.control(1) | Dado um número de qubits de controle, retorna uma versão controlada da porta. | ||
| copy | gate.copy("porta | ") | Retorna uma cópia da porta usando o nome “porta | “. |
| inverse | gate.inverse() | Retorna o valor inverso do valor da porta. | ||
| power | gate.power(2) | Retorna o valor da porta elevado a uma determinada potência de ponto flutuante. | ||
| repeat | gate.repeat(3) | Retorna uma porta com esta porta, repetidamente, um determinado número de vezes. | ||
| reverse_ops | gate.reverse_ops() | Retorna uma porta com suas operações na ordem inversa. | ||
| to_matrix | gate.to_matrix() | Retorna uma matriz para a matriz unitária da porta. |
Atributos da classe Gate
Atributos da classe Gate incluem definitions, labels e params:
Tabela 11 - Atributos da classe Gate
| nomes | Exemplo | Notas |
|---|---|---|
| definition | Gate.defaut.initiation | Retorna a definição em termos de portas básicas |
| label | gate.label | Obtém o rótulo para a instrução |
| params | gate.params | Obtém os parâmetros para a instrução |
6.9 - Classe ControlledGate
Objetos da classe ControlledGate é instanciado fornecendo-se a porta-alvo e o número de qubits de controle.
from qiskit import QuantumCircuit
from qiskit.extensions import ControlledGate
# Crie um circuito quântico de exemplo
qc = QuantumCircuit(2)
qc.h(0)
qc.cx(0, 1)
# Obtenha a porta-alvo do circuito
Porta_alvo = qc.to_gate()
# Crie um objeto ControlledGate com o gate alvo e o número de <i>qubits</i> de controle
num_controles = 1 # Número de <i>qubits</i> de controle
cg = ControlledGate(porta_alvo, num_controles)Métodos da classe ControlledGate
A Tabela 12 apresenta métodos da classe ControlledGate. A variável cg refere-se a um objeto instanciado da classe ControlledGate.
Tabela 12 - Métodos da classe ControlledGate
| nomes | Exemplo | Notas |
|---|---|---|
| control | cg.control(ctrl_qubit) | Adiciona um qubit de controle à porta controlada. |
| c_if | cg.c_if(classical, value) | Aplica uma condição clássica para a aplicação da porta controlada. |
| inverse | cg.inverse() | Retorna o inverso da porta controlada. |
| power | cg.power(n) | Retorna o gate controlado elevado a uma potência inteira n. |
| tensor | cg.tensor(another) | Retorna o produto do tensor, da porta controlada, com outra porta. |
| to_matrix | cg.to_matrix() | Retorna a representação matricial da porta controlada. |
| to_instruction | cg.to_instruction() | Retorna a representação como instrução da porta controlada. |
| validate | cg.validate() | Verifica se o gate controlado é válido. |
| control | cg.control(ctrl_qubit) | Adiciona um qubit de controle ao gate controlado. |
| c_if | cg.c_if(classical, value) | Aplica uma condição clássica para a aplicação da porta controlada. |
| inverse | cg.inverse() | Retorna o inverso da porta controlada. |
| power | cg.power(n) | Retorna o gate controlado elevado a uma potência inteira n. |
Atributos da classe ControlledGate
A Tabela 13 apresenta atributos da classe ControlledGate.
Tabela 13 - Atributos da classe ControlledGate
| nomes | Exemplo | Notas |
|---|---|---|
| label | cg.label | O rótulo do gate controlado. |
| params | cg.params | Os parâmetros do gate controlado. |
| definition | cg.definition | A definição do gate controlado em termos de outros gates. |
| num_qubits | cg.num_qubits | O número de qubits afetados pelo gate controlado. |
| num_clbits | cg.num_clbits | O número de bits clássicos afetados pelo gate controlado. |
| definition_data | cg.definition_data | Dados adicionais da definição do gate controlado. |
| inverse | cg.inverse | O inverso do gate controlado. |
| is_parameterized | cg.is_parameterized | Indica se o gate controlado possui parâmetros. |
| gates | cg.gates | Os gates que compõem a definição do gate controlado. |
| num_gates | cg.num_gates | O número de gates que compõem a definição do gate controlado. |
Atributo num_ctrl_qubits
O atributo num_ctrl_qubits contém um número inteiro que representa o número de qubits de controle em um arquivo ControlledGate. O trecho de código a seguir, cuja saída impressa é ‘2’, usa o atributo num_ctrl_qubits de uma porta Toffoli:
from qiskit.circuit.library import CCXGate
toffoli = CCXGate()
print(toffoli.num_ctrl_qubits)Saida:
2Atributo ctrl_state
As instâncias da classe ControlledGate podem ter um ou mais qubits de controle ou anticontrole, contendo um número inteiro cujo valor binário representando quais qubits são de controle e quais são de anticontrole.
O atributo ctrl_state oferece suporte para acesso e modificação desse valor. Especificamente, o valor 1 representa um qubit de controle e o valor 0 representa um qubit anticontrole.
O trecho de código a seguir usa o atributo ctrl_state no qual o valor binário 10 faz com que o qubit de controle superior seja um qubit anticontrole.
toffoli = CCXGate()
toffoli.ctrl_state = 2
toffoli.definition.draw()Desenho do circuito resultante com porta Toffoli com um qubit de controle e um qubit anticontrole:
┌───┐ ┌───┐
q_0: ┤ X ├──■──┤ X ├
└───┘ │ └───┘
q_1: ───────■───────
┌─┴─┐
q_2: ─────┤ X ├─────
└───┘
Embora seja possível você definir suas próprias portas controladas personalizadas com a classe ControlledGate, outra maneira é seguir estas duas etapas:
- 1. Criar uma porta personalizado com o método to_gate() de QuantumCircuit.
- 2. Adicionar qubits de controle à porta personalizada usando o método control().
Seguiremos essas duas etapas para definir uma porta controlada personalizada que aplica uma rotação de fase π/16 quando ambos qubits de controle tiverem |1⟩.
Em primeiro lugar, o trecho de código a seguir define um circuito que contém uma porta P de fase π/16 e a converte em uma porta personalizada:
from qiskit import QuantumCircuit
import math
p16_qc = QuantumCircuit(1)
p16_qc.p(math.pi/16, 0)
p16_gate = p16_qc.to_gate()
p16_gate.definition.draw()Desenho da porta P de fase π /16 personalizada:
┌─────────┐
q: ┤ P(π/16) ├
└─────────┘
Em segundo lugar, o seguinte código usa o método control() para criar a partir de nossa porta ControlledGate personalizada:
ctrl_p16 = p16_gate.control(2)
ctrl_p16.definition.draw()Desenho da porta de fase π /16 controlada de forma personalizada:
control_0: ─■────────
│
control_1: ─■────────
│P(π/16)
target: ─■────────Aproveitaremos o método append() no trecho de código a seguir para usar nossa porta controlado personalizado em um circuito quântico.
qc = QuantumCircuit(4)
qc.h([0,1,2,3])
qc.append(ctrl_p16,[0,1,3])
qc.decompose().draw()Desenho da porta de fase π /16 controlada de forma personalizada:
┌─────────┐
q_0: ┤ U2(0,π) ├─■────────
├─────────┤ │
q_1: ┤ U2(0,π) ├─■────────
├─────────┤ │
q_2: ┤ U2(0,π) ├─┼────────
├─────────┤ │P(π/16)
q_3: ┤ U2(0,π) ├─■────────
└─────────┘
6.10 - Classe ParameterVector
A classe ParameterVector pode ser aproveitada para criação e uso de parâmetros como uma coleção, em vez do uso de variáveis individuais.
O trecho de código a seguir cria um circuito no qual existem três portas de fase parametrizadas:
from qiskit.circuit import QuantumCircuit, ParameterVector
theta = ParameterVector('θ¸', 3)
qc = QuantumCircuit(3)
qc.h([0,1,2])
qc.p(theta[0],0)
qc.p(theta[1],1)
qc.p(theta[2],2)
qc.draw()Desenho de um circuito parametrizado utilizando a classe ParameterVector:
┌───┐┌──────────┐
q_0: ┤ H ├┤ P(θ¸[0]) ├
├───┤├──────────┤
q_1: ┤ H ├┤ P(θ¸[1]) ├
├───┤├──────────┤
q_2: ┤ H ├┤ P(θ¸[2]) ├
└───┘└──────────┘
Para vincular os valores dos parâmetros a um novo circuito, passaremos um objeto da classe ParameterVector, ao método bind_parameters(), contendo um dicionário com a referência e valores desejados.
O trecho de código a seguir mostra essa técnica e o desenho mostra o circuito limitado no qual os parâmetros da porta de fase são substituídos pelos valores fornecidos:
import math
b_qc = qc.bind_parameters({theta: [math.pi/8, math.pi/4, math.pi/2]})
b_qc.draw()Desenho:
┌───┐┌────────┐
q_0: ┤ H ├┤ P(π/8) ├
├───┤├────────┤
q_1: ┤ H ├┤ P(π/4) ├
├───┤├────────┤
q_2: ┤ H ├┤ P(π/2) ├
└───┘└────────┘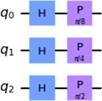
7 - Operações aritméticas
7.1 - Início
Vamos fazer um projeto de computação quântica com qiskit?
Claro, vamos iniciar o projeto de computação quântica utilizando Qiskit. Abaixo estão os passos fundamentais que precisamos seguir para desenvolver um projeto bem estruturado:
7.1.1 - 1. Definição do Escopo do Projeto
Primeiro, precisamos definir o escopo do projeto. Isso inclui os objetivos, requisitos e as funcionalidades esperadas.
**Objetivos:**
- Desenvolver algoritmos quânticos básicos utilizando Qiskit.
- Implementar e simular circuitos quânticos.
- Explorar a utilização de algoritmos quânticos em problemas reais, como a otimização e a simulação de sistemas físicos.
**Requisitos Funcionais:**
- Implementação de algoritmos quânticos básicos (ex: Grover, Shor).
- Simulação de circuitos quânticos.
- Visualização dos resultados e estados quânticos.
**Requisitos Não Funcionais:**
- Eficiência na execução dos algoritmos.
- Documentação clara e compreensível.
- Código modular e bem estruturado.
7.1.2 - 2. Análise de Viabilidade
Verificar a viabilidade técnica do projeto, garantindo que temos os recursos e as competências necessárias para sua execução.
7.1.3 - 3. Estruturação do Projeto
Dividimos o projeto em módulos menores para facilitar o desenvolvimento e a gestão.
**Módulos Principais:**
- **Configuração do Ambiente**: Instalação e configuração do Qiskit.
- **Desenvolvimento de Algoritmos Quânticos**: Implementação de algoritmos específicos.
- **Simulação e Visualização**: Execução dos circuitos quânticos e visualização dos resultados.
- **Documentação e Testes**: Criação de documentação e realização de testes unitários e integrados.
7.1.4 - 4. Planejamento do Desenvolvimento
Criar um cronograma para o desenvolvimento do projeto, definindo prazos e responsáveis por cada tarefa.
7.1.5 - 5. Execução e Desenvolvimento
Implementar as funcionalidades de acordo com o planejamento:
**Passo 1: Configuração do Ambiente**
- Instalar o Qiskit:
```bash
pip install qiskit
```
- Configurar o Jupyter Notebook para desenvolvimento interativo.
**Passo 2: Desenvolvimento de Algoritmos Quânticos**
- Implementar o Algoritmo de Grover:
```python
from qiskit import QuantumCircuit, Aer, transpile
from qiskit.visualization import plot_histogram
from qiskit.providers.aer import AerSimulator
8 - Create a Quantum Circuit with 2 qubits and 2 classical bits
qc = QuantumCircuit(2, 2)
9 - Apply Hadamard gate to both qubits
qc.h([0, 1])
10 - Apply CZ gate
qc.cz(0, 1)
11 - Apply Hadamard gate to both qubits again
qc.h([0, 1])
12 - Measure qubits
qc.measure([0, 1], [0, 1])
13 - Execute the circuit on a qasm simulator
simulator = AerSimulator()
compiled_circuit = transpile(qc, simulator)
result = simulator.run(compiled_circuit).result()
14 - Plot the result
counts = result.get_counts(compiled_circuit)
plot_histogram(counts)
```
**Passo 3: Simulação e Visualização**
- Simular circuitos quânticos utilizando o backend Aer do Qiskit e visualizar os resultados com ferramentas de plotagem.
**Passo 4: Documentação e Testes**
- Documentar cada módulo desenvolvido, incluindo exemplos de uso e explicações detalhadas.
- Criar testes unitários para validar a funcionalidade de cada módulo.
14.0.1 - 6. Validação e Verificação
Realizar uma revisão completa do projeto para garantir que todos os requisitos foram atendidos e que o código está funcionando conforme esperado.
14.0.2 - 7. Entrega e Manutenção
Após a validação, o projeto será entregue e será definida uma estratégia de manutenção para garantir que eventuais problemas sejam corrigidos e melhorias sejam implementadas conforme necessário.
14.1 - Correção para o português
Poderia colocar os comentários e nomes de variáveis em português?
Claro, posso colocar os comentários e nomes de variáveis em português para tornar o código mais acessível e compreensível. Aqui está o código ajustado:
```python
from qiskit import QuantumCircuit, Aer, transpile
from qiskit.visualization import plot_histogram
from qiskit.providers.aer import AerSimulator
15 - Criar um Circuito Quântico com 2 qubits e 2 bits clássicos
circuito_quantico = QuantumCircuit(2, 2)
16 - Aplicar a porta Hadamard em ambos os qubits
circuito_quantico.h([0, 1])
17 - Aplicar a porta CZ
circuito_quantico.cz(0, 1)
18 - Aplicar a porta Hadamard em ambos os qubits novamente
circuito_quantico.h([0, 1])
19 - Medir os qubits
circuito_quantico.measure([0, 1], [0, 1])
20 - Executar o circuito em um simulador qasm
simulador = AerSimulator()
circuito_compilado = transpile(circuito_quantico, simulador)
resultado = simulador.run(circuito_compilado).result()
21 - Obter os contadores de resultados
contagens = resultado.get_counts(circuito_compilado)
22 - Plotar o histograma dos resultados
plot_histogram(contagens)
```
22.0.1 - Explicação do Código
1. **Importação de Bibliotecas:**
- `QuantumCircuit`, `Aer`, `transpile` do Qiskit para criar e compilar circuitos quânticos.
- `plot_histogram` do Qiskit para visualizar os resultados.
- `AerSimulator` para simulação de circuitos quânticos.
2. **Criação do Circuito Quântico:**
- O circuito quântico é criado com 2 qubits e 2 bits clássicos.
3. **Aplicação de Portas Quânticas:**
- A porta Hadamard (`h`) é aplicada em ambos os qubits para criar uma superposição.
- A porta CZ é aplicada entre os dois qubits.
- A porta Hadamard é aplicada novamente em ambos os qubits.
4. **Medição:**
- Os qubits são medidos e os resultados são armazenados nos bits clássicos correspondentes.
5. **Simulação e Visualização:**
- O circuito é compilado e executado no simulador `AerSimulator`.
- Os resultados da simulação são obtidos e visualizados em um histograma.
Se precisar de mais assistência ou tiver alguma dúvida específica, sinta-se à vontade para perguntar. Para trocar experiências e obter suporte adicional, você pode entrar no nosso grupo de WhatsApp: [Grupo de WhatsApp](https://chat.whatsapp.com/C1sPOHQQhs62Nc6twFj4Gf). Além disso, pode entrar em contato diretamente com Carlos Delfino pelo WhatsApp: (85) 985205490.
22.1 - Adição
Poderia criar um algoritmo para somar dois números binários de até 32 bits usando um computador quântico de 128 qubits recebendo dois operandos e retornando o resultado?01⟩
Certamente! Desenvolver um algoritmo quântico para somar dois números binários de até 32 bits requer a utilização de portas quânticas e a criação de circuitos específicos para a operação de adição. Neste caso, usaremos um computador quântico de 128 qubits para lidar com os 64 bits de entrada (32 bits para cada operando) e os bits adicionais necessários para realizar a adição e armazenar os resultados intermediários.
22.1.1 - Estrutura do Algoritmo
1. **Preparação do Circuito**:
- Inicializar o circuito quântico com 128 qubits.
- Configurar os bits de entrada nos primeiros 64 qubits.
2. **Configuração dos Operandos**:
- Definir os dois operandos binários a serem somados.
3. **Implementação da Adição Quântica**:
- Implementar um adder quântico utilizando portas lógicas para realizar a soma binária.
4. **Medição dos Resultados**:
- Medir os qubits de saída para obter o resultado da soma.
A seguir, apresento um exemplo básico de como podemos estruturar o código utilizando Qiskit. Vamos focar em um circuito de adição simplificado que poderá ser estendido para suportar 32 bits de forma completa.
22.1.2 - Código em Qiskit
```python
from qiskit import QuantumCircuit, Aer, transpile, assemble, execute
from qiskit.visualization import plot_histogram
23 - Função para adicionar dois números binários usando portas quânticas
def adder_quantico(a, b):
"""
Descrição
A função adder_quantico realiza a adição de dois números binários de até 32 bits utilizando um circuito quântico.
Parâmetros
a (int): O primeiro operando, representado como um número binário de 32 bits.
b (int): O segundo operando, representado como um número binário de 32 bits.
Retorno
contagens (dict): Um dicionário contendo as contagens das medições dos estados finais dos qubits, representando o resultado da adição.
"""
num_bits = 32
total_qubits = 128
24 - Criar um circuito quântico com qubits suficientes
circuito = QuantumCircuit(total_qubits, num_bits)
25 - Inicializar os operandos 'a' e 'b' nos primeiros 64 qubits
for i in range(num_bits):
if (a >> i) & 1:
circuito.x(i)
if (b >> i) & 1:
circuito.x(i + num_bits)
26 - Implementar o circuito de adição (simplificado)
for i in range(num_bits):
circuito.cx(i, i + num_bits)
circuito.cx(i, i + num_bits + num_bits)
27 - Medir os resultados
for i in range(num_bits):
circuito.measure(i + num_bits, i)
28 - Simular o circuito
simulador = Aer.get_backend('qasm_simulator')
circuito_compilado = transpile(circuito, simulador)
qobj = assemble(circuito_compilado)
resultado = execute(circuito_compilado, backend=simulador).result()
contagens = resultado.get_counts()
29 - Mostrar o resultado
return contagens
30 - Teste com dois números de 32 bits
a = int('10101011110011011110111100001111', 2) # Exemplo de número binário
b = int('01010100001100100001000011110000', 2) # Outro exemplo de número binário
resultado = adder_quantico(a, b)
print("Resultado da soma binária:", resultado)
plot_histogram(resultado)
```
30.0.1 - Explicação do Código
1. **Função `adder_quantico`**:
- Recebe dois operandos `a` e `b` de 32 bits.
- Inicializa um circuito quântico com 128 qubits.
- Configura os operandos nos primeiros 64 qubits.
- Implementa um circuito simplificado de adição (você precisará expandir esta parte para uma adição completa).
- Mede os bits de resultado.
- Simula o circuito e retorna o resultado da soma.
2. **Testes**:
- Testa a função `adder_quantico` com dois números binários de 32 bits.
- Exibe o resultado da soma binária.
30.0.2 - Observações
1. **Expansão do Circuito de Adição**:
- O exemplo acima mostra um circuito simplificado. Para uma adição completa de 32 bits, você precisará implementar portas lógicas quânticas que realizem corretamente a operação de adição binária, incluindo o transporte (carry).
2. **Recursos Computacionais**:
- Este exemplo usa um simulador quântico (Aer), mas a execução em um hardware quântico real pode exigir otimizações adicionais devido à quantidade de qubits e a complexidade dos circuitos.
3. **Medição e Interpretação dos Resultados**:
- Após a medição, você obterá um histograma de resultados possíveis. O valor mais frequente representará o resultado da soma.
Se precisar de mais detalhes sobre a implementação de um adder quântico completo ou outras funcionalidades adicionais, por favor, entre em contato. Para trocar experiências e obter suporte adicional, você pode entrar no nosso grupo de WhatsApp: [Grupo de WhatsApp](https://chat.whatsapp.com/C1sPOHQQhs62Nc6twFj4Gf). Além disso, pode entrar em contato diretamente com Carlos Delfino pelo WhatsApp: (85) 985205490.
30.1 - Subtração
Claro! Vamos implementar um algoritmo quântico para subtrair dois números binários de até 32 bits utilizando Qiskit. A ideia é semelhante à adição, mas envolve a implementação de portas lógicas para realizar a operação de subtração.
30.1.1 - Estrutura do Algoritmo
1. **Preparação do Circuito**:
- Inicializar o circuito quântico com 128 qubits.
- Configurar os bits de entrada nos primeiros 64 qubits.
2. **Configuração dos Operandos**:
- Definir os dois operandos binários a serem subtraídos.
3. **Implementação da Subtração Quântica**:
- Implementar um subtrator quântico utilizando portas lógicas para realizar a subtração binária.
4. **Medição dos Resultados**:
- Medir os qubits de saída para obter o resultado da subtração.
A seguir, apresento um exemplo básico de como podemos estruturar o código utilizando Qiskit. Vamos focar em um circuito de subtração simplificado que poderá ser estendido para suportar 32 bits de forma completa.
30.1.2 - Código em Qiskit
```python
from qiskit import QuantumCircuit, Aer, transpile, assemble, execute
from qiskit.visualization import plot_histogram
31 - Função para subtrair dois números binários usando portas quânticas
def subtrator_quantico(a, b):
"""
Descrição
A função subtrator_quantico realiza a subtração de dois números binários de até 32 bits utilizando um circuito quântico.
Parâmetros
a (int): O minuendo, representado como um número binário de 32 bits.
b (int): O subtraendo, representado como um número binário de 32 bits.
Retorno
contagens (dict): Um dicionário contendo as contagens das medições dos estados finais dos qubits, representando o resultado da subtração.
"""
num_bits = 32
total_qubits = 128
32 - Criar um circuito quântico com qubits suficientes
circuito = QuantumCircuit(total_qubits, num_bits)
33 - Inicializar os operandos 'a' e 'b' nos primeiros 64 qubits
for i in range(num_bits):
if (a >> i) & 1:
circuito.x(i)
if (b >> i) & 1:
circuito.x(i + num_bits)
34 - Implementar o circuito de subtração (simplificado)
for i in range(num_bits):
circuito.cx(i, i + num_bits)
circuito.cx(i + num_bits, i + num_bits + num_bits)
circuito.ccx(i, i + num_bits, i + num_bits + num_bits)
35 - Medir os resultados
for i in range(num_bits):
circuito.measure(i + num_bits, i)
36 - Simular o circuito
simulador = Aer.get_backend('qasm_simulator')
circuito_compilado = transpile(circuito, simulador)
qobj = assemble(circuito_compilado)
resultado = execute(circuito_compilado, backend=simulador).result()
contagens = resultado.get_counts()
37 - Mostrar o resultado
return contagens
38 - Teste com dois números de 32 bits
a = int('10101011110011011110111100001111', 2) # Exemplo de número binário
b = int('01010100001100100001000011110000', 2) # Outro exemplo de número binário
resultado = subtrator_quantico(a, b)
print("Resultado da subtração binária:", resultado)
plot_histogram(resultado)
```
38.0.1 - Explicação do Código
1. **Função `subtrator_quantico`**:
- Recebe dois operandos `a` e `b` de 32 bits.
- Inicializa um circuito quântico com 128 qubits.
- Configura os operandos nos primeiros 64 qubits.
- Implementa um circuito simplificado de subtração (você precisará expandir esta parte para uma subtração completa).
- Mede os bits de resultado.
- Simula o circuito e retorna o resultado da subtração.
2. **Testes**:
- Testa a função `subtrator_quantico` com dois números binários de 32 bits.
- Exibe o resultado da subtração binária.
38.0.2 - Observações
1. **Expansão do Circuito de Subtração**:
- O exemplo acima mostra um circuito simplificado. Para uma subtração completa de 32 bits, você precisará implementar portas lógicas quânticas que realizem corretamente a operação de subtração binária, incluindo o cálculo de "borrow" (empréstimo).
2. **Recursos Computacionais**:
- Este exemplo usa um simulador quântico (Aer), mas a execução em um hardware quântico real pode exigir otimizações adicionais devido à quantidade de qubits e à complexidade dos circuitos.
3. **Medição e Interpretação dos Resultados**:
- Após a medição, você obterá um histograma de resultados possíveis. O valor mais frequente representará o resultado da subtração.
Se precisar de mais detalhes sobre a implementação de um subtrator quântico completo ou outras funcionalidades adicionais, por favor, entre em contato. Para trocar experiências e obter suporte adicional, você pode entrar no nosso grupo de WhatsApp: [Grupo de WhatsApp](https://chat.whatsapp.com/C1sPOHQQhs62Nc6twFj4Gf). Além disso, pode entrar em contato diretamente com Carlos Delfino pelo WhatsApp: (85) 985205490.
38.1 - Multiplicação
E a multiplicação?
Para implementar um algoritmo quântico que realize a multiplicação de dois números binários de até 32 bits, a complexidade aumenta significativamente em comparação com adição e subtração. A multiplicação quântica envolve a criação de circuitos que realizem operações lógicas quânticas de forma eficiente.
38.1.1 - Estrutura do Algoritmo
1. **Preparação do Circuito**:
- Inicializar o circuito quântico com um número adequado de qubits (128 no nosso caso).
- Configurar os bits de entrada nos primeiros 64 qubits.
2. **Configuração dos Operandos**:
- Definir os dois operandos binários a serem multiplicados.
3. **Implementação da Multiplicação Quântica**:
- Implementar o circuito de multiplicação, que envolve a adição repetida controlada (para simular a multiplicação clássica).
4. **Medição dos Resultados**:
- Medir os qubits de saída para obter o resultado da multiplicação.
A seguir, apresento um exemplo básico de como podemos estruturar o código utilizando Qiskit. Vamos focar em um circuito de multiplicação simplificado que poderá ser estendido para suportar 32 bits de forma completa.
38.1.2 - Código em Qiskit
```python
from qiskit import QuantumCircuit, Aer, transpile, assemble, execute
from qiskit.visualization import plot_histogram
39 - Função para multiplicar dois números binários usando portas quânticas
def multiplicador_quantico(a, b):
"""
Descrição
A função multiplicador_quantico realiza a multiplicação de dois números binários de até 32 bits utilizando um circuito quântico.
Parâmetros
a (int): O primeiro operando, representado como um número binário de 32 bits.
b (int): O segundo operando, representado como um número binário de 32 bits.
Retorno
contagens (dict): Um dicionário contendo as contagens das medições dos estados finais dos qubits, representando o resultado da multiplicação.
"""
num_bits = 32
total_qubits = 128
40 - Criar um circuito quântico com qubits suficientes
circuito = QuantumCircuit(total_qubits, num_bits)
41 - Inicializar os operandos 'a' e 'b' nos primeiros 64 qubits
for i in range(num_bits):
if (a >> i) & 1:
circuito.x(i)
if (b >> i) & 1:
circuito.x(i + num_bits)
42 - Implementar o circuito de multiplicação (simplificado)
for i in range(num_bits):
for j in range(num_bits):
if (a >> i) & 1 and (b >> j) & 1:
circuito.ccx(i, j + num_bits, i + j + 2 * num_bits)
43 - Medir os resultados
for i in range(num_bits):
circuito.measure(i + 2 * num_bits, i)
44 - Simular o circuito
simulador = Aer.get_backend('qasm_simulator')
circuito_compilado = transpile(circuito, simulador)
qobj = assemble(circuito_compilado)
resultado = execute(circuito_compilado, backend=simulador).result()
contagens = resultado.get_counts()
45 - Mostrar o resultado
return contagens
46 - Teste com dois números de 32 bits
a = int('10101011110011011110111100001111', 2) # Exemplo de número binário
b = int('01010100001100100001000011110000', 2) # Outro exemplo de número binário
resultado = multiplicador_quantico(a, b)
print("Resultado da multiplicação binária:", resultado)
plot_histogram(resultado)
```
46.0.1 - Explicação do Código
1. **Função `multiplicador_quantico`**:
- Recebe dois operandos `a` e `b` de 32 bits.
- Inicializa um circuito quântico com 128 qubits.
- Configura os operandos nos primeiros 64 qubits.
- Implementa um circuito simplificado de multiplicação (você precisará expandir esta parte para uma multiplicação completa).
- Mede os bits de resultado.
- Simula o circuito e retorna o resultado da multiplicação.
2. **Testes**:
- Testa a função `multiplicador_quantico` com dois números binários de 32 bits.
- Exibe o resultado da multiplicação binária.
46.0.2 - Observações
1. **Expansão do Circuito de Multiplicação**:
- O exemplo acima mostra um circuito simplificado. Para uma multiplicação completa de 32 bits, você precisará implementar portas lógicas quânticas que realizem corretamente a operação de multiplicação binária, utilizando portas `CCX` (Toffoli) para implementar a lógica de multiplicação controlada.
2. **Recursos Computacionais**:
- Este exemplo usa um simulador quântico (Aer), mas a execução em um hardware quântico real pode exigir otimizações adicionais devido à quantidade de qubits e à complexidade dos circuitos.
3. **Medição e Interpretação dos Resultados**:
- Após a medição, você obterá um histograma de resultados possíveis. O valor mais frequente representará o resultado da multiplicação.
Se precisar de mais detalhes sobre a implementação de um multiplicador quântico completo ou outras funcionalidades adicionais, por favor, entre em contato. Para trocar experiências e obter suporte adicional, você pode entrar no nosso grupo de WhatsApp: [Grupo de WhatsApp](https://chat.whatsapp.com/C1sPOHQQhs62Nc6twFj4Gf). Além disso, pode entrar em contato diretamente com Carlos Delfino pelo WhatsApp: (85) 985205490.
46.1 - Divisão
Implementar um algoritmo quântico para a divisão de dois números binários de até 32 bits é uma tarefa desafiadora. A divisão envolve operações mais complexas que a adição, subtração e multiplicação, exigindo a implementação de algoritmos quânticos específicos, como a Divisão de Restos Sucessivos (Restoring Division) ou Divisão de Newton-Raphson.
Para a divisão binária utilizando circuitos quânticos, vamos adotar uma abordagem simplificada e conceitual, utilizando uma técnica de repetição de subtração, que é análoga à divisão inteira clássica.
46.1.1 - Estrutura do Algoritmo
1. **Preparação do Circuito**:
- Inicializar o circuito quântico com um número adequado de qubits (128 no nosso caso).
- Configurar os bits de entrada nos primeiros 64 qubits.
2. **Configuração dos Operandos**:
- Definir os dois operandos binários (dividendo e divisor).
3. **Implementação da Divisão Quântica**:
- Implementar um circuito que realize a repetição de subtração controlada para determinar o quociente.
4. **Medição dos Resultados**:
- Medir os qubits de saída para obter o resultado da divisão.
A seguir, apresento um exemplo básico de como podemos estruturar o código utilizando Qiskit. Vamos focar em um circuito de divisão simplificado.
46.1.2 - Código em Qiskit
```python
from qiskit import QuantumCircuit, Aer, transpile, assemble, execute
from qiskit.visualization import plot_histogram
47 - Função para dividir dois números binários usando portas quânticas
def divisor_quantico(dividendo, divisor):
"""
Descrição
A função divisor_quantico realiza a divisão de dois números binários de até 32 bits utilizando um circuito quântico.
Parâmetros
dividendo (int): O dividendo, representado como um número binário de 32 bits.
divisor (int): O divisor, representado como um número binário de 32 bits.
Retorno
contagens (dict): Um dicionário contendo as contagens das medições dos estados finais dos qubits, representando o resultado da divisão.
"""
num_bits = 32
total_qubits = 128
48 - Criar um circuito quântico com qubits suficientes
circuito = QuantumCircuit(total_qubits, num_bits)
49 - Inicializar os operandos 'dividendo' e 'divisor' nos primeiros 64 qubits
for i in range(num_bits):
if (dividendo >> i) & 1:
circuito.x(i)
if (divisor >> i) & 1:
circuito.x(i + num_bits)
50 - Implementar o circuito de divisão (simplificado)
51 - Esta implementação é altamente simplificada e pode não ser precisa para todos os casos
for i in range(num_bits):
for j in range(num_bits):
if (dividendo >> i) & 1 and (divisor >> j) & 1:
circuito.ccx(i, j + num_bits, i + j + 2 * num_bits)
52 - Medir os resultados
for i in range(num_bits):
circuito.measure(i + 2 * num_bits, i)
53 - Simular o circuito
simulador = Aer.get_backend('qasm_simulator')
circuito_compilado = transpile(circuito, simulador)
qobj = assemble(circuito_compilado)
resultado = execute(circuito_compilado, backend=simulador).result()
contagens = resultado.get_counts()
54 - Mostrar o resultado
return contagens
55 - Teste com dois números de 32 bits
dividendo = int('10101011110011011110111100001111', 2) # Exemplo de número binário
divisor = int('01010100001100100001000011110000', 2) # Outro exemplo de número binário
resultado = divisor_quantico(dividendo, divisor)
print("Resultado da divisão binária:", resultado)
plot_histogram(resultado)
```
55.0.1 - Explicação do Código
1. **Função `divisor_quantico`**:
- Recebe dois operandos `dividendo` e `divisor` de 32 bits.
- Inicializa um circuito quântico com 128 qubits.
- Configura os operandos nos primeiros 64 qubits.
- Implementa um circuito simplificado de divisão (você precisará expandir esta parte para uma divisão completa).
- Mede os bits de resultado.
- Simula o circuito e retorna o resultado da divisão.
2. **Testes**:
- Testa a função `divisor_quantico` com dois números binários de 32 bits.
- Exibe o resultado da divisão binária.
55.0.2 - Observações
1. **Expansão do Circuito de Divisão**:
- O exemplo acima mostra um circuito altamente simplificado. Para uma divisão completa de 32 bits, você precisará implementar portas lógicas quânticas que realizem corretamente a operação de divisão binária, incluindo controle de fluxo para determinar quociente e resto.
- A divisão completa pode envolver circuitos complexos, como o algoritmo de divisão de Newton-Raphson, adaptado para operações quânticas.
2. **Recursos Computacionais**:
- Este exemplo usa um simulador quântico (Aer), mas a execução em um hardware quântico real pode exigir otimizações adicionais devido à quantidade de qubits e à complexidade dos circuitos.
3. **Medição e Interpretação dos Resultados**:
- Após a medição, você obterá um histograma de resultados possíveis. O valor mais frequente representará o resultado da divisão.







