Matplotlib

Carregando, aguarde alguns segundos.

9 - Galeria Matplotlib

9.1 - Gráficos 3d

9.1.1 - Gráfico de dispersão 3D

from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

# Gere alguns dados de amostra 3D
mu_vec1 = np.array([0,0,0]) # mean vector
cov_mat1 = np.array([[1,0,0],[0,1,0],[0,0,1]]) # covariance matrix

class1_sample = np.random.multivariate_normal(mu_vec1, cov_mat1, 20)
class2_sample = np.random.multivariate_normal(mu_vec1 + 1, cov_mat1, 20)
class3_sample = np.random.multivariate_normal(mu_vec1 + 2, cov_mat1, 20)

# class1_sample.shape -> (20, 3), 20 linhas, 3 colunas

fig = plt.figure(figsize=(8,8))
ax = fig.add_subplot(111, projection='3d')
   
ax.scatter(
    class1_sample[:,0], class1_sample[:,1], class1_sample[:,2], 
    marker='x', color='blue', s=40, label='class 1')
ax.scatter(
    class2_sample[:,0], class2_sample[:,1], class2_sample[:,2], 
    marker='o', color='green', s=40, label='class 2')
ax.scatter(
    class3_sample[:,0], class3_sample[:,1], class3_sample[:,2], 
    marker='^', color='red', s=40, label='class 3')

ax.set_xlabel('variable X')
ax.set_ylabel('variable Y')
ax.set_zlabel('variable Z')

plt.title('Gráfico de dispersão 3D')
     
plt.show()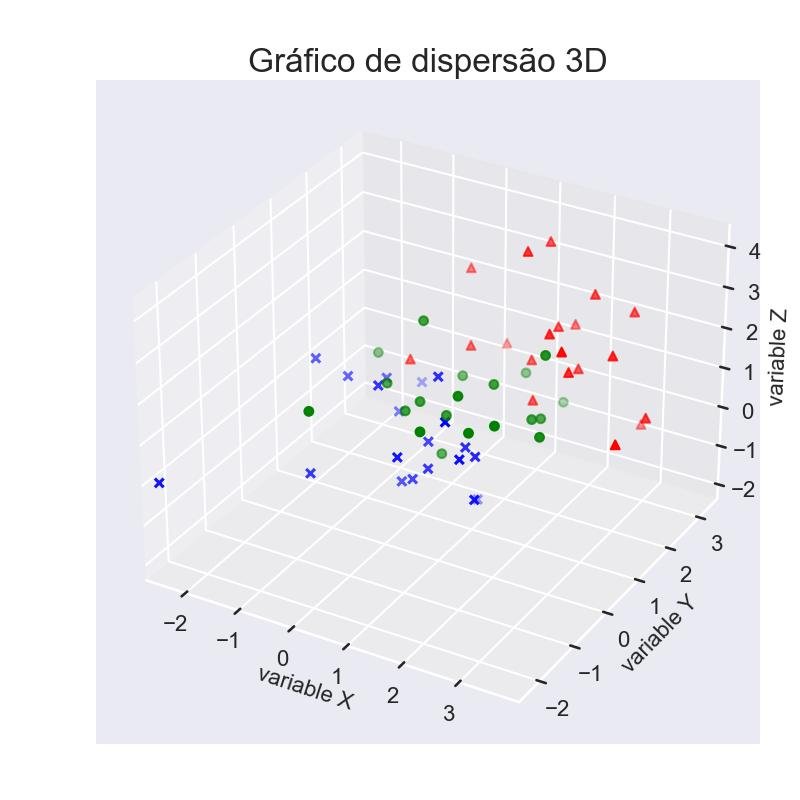

9.1.2 - Gráfico de dispersão 3D com autovetores

import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.patches import FancyArrowPatch
from mpl_toolkits.mplot3d import proj3d

class Arrow3D(FancyArrowPatch):
    def __init__(self, xs, ys, zs, *args, **kwargs):
        FancyArrowPatch.__init__(self, (0,0), (0,0), *args, **kwargs)
        self._verts3d = xs, ys, zs

        
    def do_3d_projection(self, renderer=None):
        xs3d, ys3d, zs3d = self._verts3d
        xs, ys, zs = proj3d.proj_transform(xs3d, ys3d, zs3d, self.axes.M)
        self.set_positions((xs[0],ys[0]),(xs[1],ys[1]))
        return np.min(zs)

# Gerar alguns dados de exemplo
mu_vec1 = np.array([0,0,0])
cov_mat1 = np.array([[1,0,0],[0,1,0],[0,0,1]])
class1_sample = np.random.multivariate_normal(mu_vec1, cov_mat1, 20)

mu_vec2 = np.array([1,1,1])
cov_mat2 = np.array([[1,0,0],[0,1,0],[0,0,1]])
class2_sample = np.random.multivariate_normal(mu_vec2, cov_mat2, 20)

# concatenar dados para PCA
amostras = np.concatenate((class1_sample, class2_sample), axis=0)

# valores médios
mean_x = np.mean(amostras[:,0])
mean_y = np.mean(amostras[:,1])
mean_z = np.mean(amostras[:,2])

# autovetores e autovalores
eig_val, eig_vec = np.linalg.eig(cov_mat1)

###############################
# plotagem de autovetores
###############################

fig = plt.figure(figsize=(10,10))
ax = fig.add_subplot(111, projection='3d')

ax.plot(amostras[:,0], amostras[:,1], amostras[:,2], 'o', markersize=10, color='green', alpha=0.2)
ax.plot([mean_x], [mean_y], [mean_z], 'o', markersize=10, color='red', alpha=0.5)
for v in eig_vec.T:
    a = Arrow3D([mean_x, v[0]], [mean_y, v[1]], 
                [mean_z, v[2]], mutation_scale=20, lw=3, arrowstyle="-|>", color="r")
    ax.add_artist(a)
ax.set_xlabel('variable X')
ax.set_ylabel('variable Y')
ax.set_zlabel('variable Z')

plt.title('Gráfico de dispersão 3D com autovetores')

plt.show()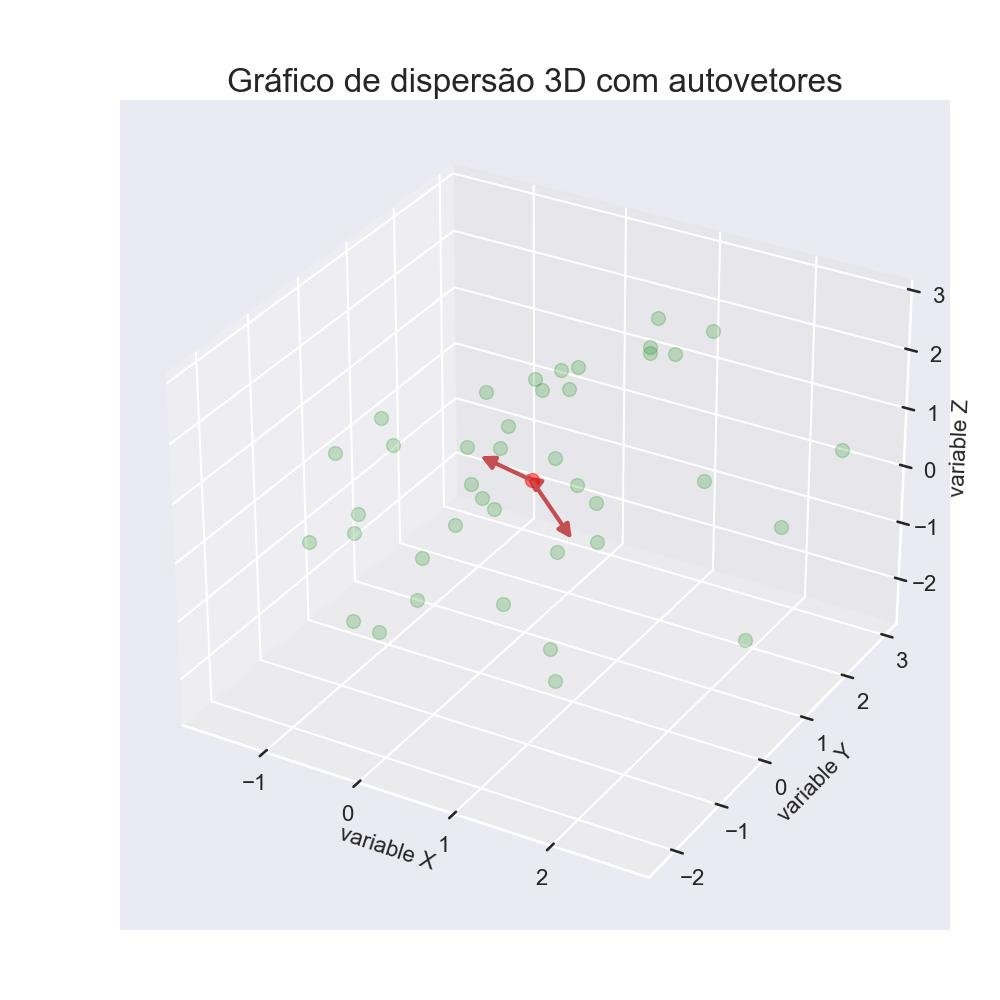

9.1.3 - Cubo 3D

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
from itertools import product, combinations
fig = plt.figure(figsize=(7,7))
ax = fig.gca(projection='3d')
ax.set_aspect("auto")

# Pontos de plotagem

# Amostras dentro do cubo

X_inside = np.array([[0,0,0],[0.2,0.2,0.2],[0.1, -0.1, -0.3]])

X_outside = np.array([[-1.2,0.3,-0.3],[0.8,-0.82,-0.9],[1, 0.6, -0.7],
                      [0.8,0.7,0.2],[0.7,-0.8,-0.45],[-0.3, 0.6, 0.9],
                      [0.7,-0.6,-0.8]])

for row in X_inside:
    ax.scatter(row[0], row[1], row[2], color="r", s=50, marker='^')

for row in X_outside:    
    ax.scatter(row[0], row[1], row[2], color="k", s=50)

# Cubo de plotagem

h = [-0.5, 0.5]
for s, e in combinations(np.array(list(product(h,h,h))), 2):
    if np.sum(np.abs(s-e)) == h[1]-h[0]:
        ax.plot3D(*zip(s,e), color="g")

ax.set_xlim(-1.5, 1.5)
ax.set_ylim(-1.5, 1.5)
ax.set_zlim(-1.5, 1.5)

plt.show()

9.1.4 - Distribuição gaussiana multivariada com superfície colorida

import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def bivariate_normal(X, Y, sigmax=1.0, sigmay=1.0, mux=0.0, muy=0.0, sigmaxy=0.0):
    """
    Distribuição gaussiana bivariada para formas iguais *X*, *Y*.
    Veja em mathworld: <a href='http://mathworld.wolfram.com/BivariateNormalDistribution.html'>bivariate normal distribution</a>.
    """
    Xmu = X-mux
    Ymu = Y-muy
    rho = sigmaxy/(sigmax*sigmay)
    z = Xmu**2/sigmax**2 + Ymu**2/sigmay**2 - 2*rho*Xmu*Ymu/(sigmax*sigmay)
    denom = 2*np.pi*sigmax*sigmay*np.sqrt(1-rho**2)
    return np.exp(-z/(2*(1-rho**2))) / denom
fig = plt.figure(figsize=(10, 7))
ax = fig.gca(projection='3d')
x = np.linspace(-5, 5, 200)
y = x
X,Y = np.meshgrid(x, y)
Z = bivariate_normal(X, Y)
surf = ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=plt.cm.coolwarm,
        linewidth=0, antialiased=False)

ax.set_zlim(0, 0.2)

ax.zaxis.set_major_locator(plt.LinearLocator(10))
ax.zaxis.set_major_formatter(plt.FormatStrFormatter('%.02f'))

fig.colorbar(surf, shrink=0.5, aspect=7, cmap=plt.cm.coolwarm)

plt.show()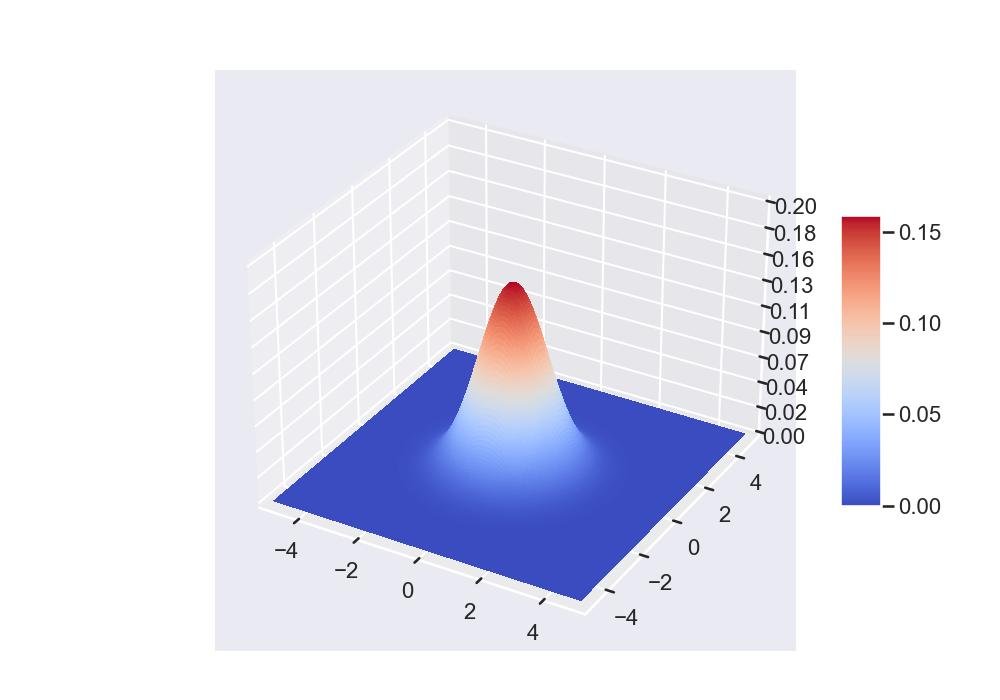

9.1.5 - Distribuição gaussiana multivariada como grade de malha

import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure(figsize=(10, 7))
ax = fig.gca(projection='3d')
x = np.linspace(-5, 5, 200)
y = x
X,Y = np.meshgrid(x, y)
Z = bivariate_normal(X, Y)
surf = ax.plot_wireframe(X, Y, Z, rstride=4, cstride=4, color='g', alpha=0.7)

ax.set_zlim(0, 0.2)

ax.zaxis.set_major_locator(plt.LinearLocator(10))
ax.zaxis.set_major_formatter(plt.FormatStrFormatter('%.02f'))

ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('p(x)')

plt.title('Gaussiano bivariado')

plt.show()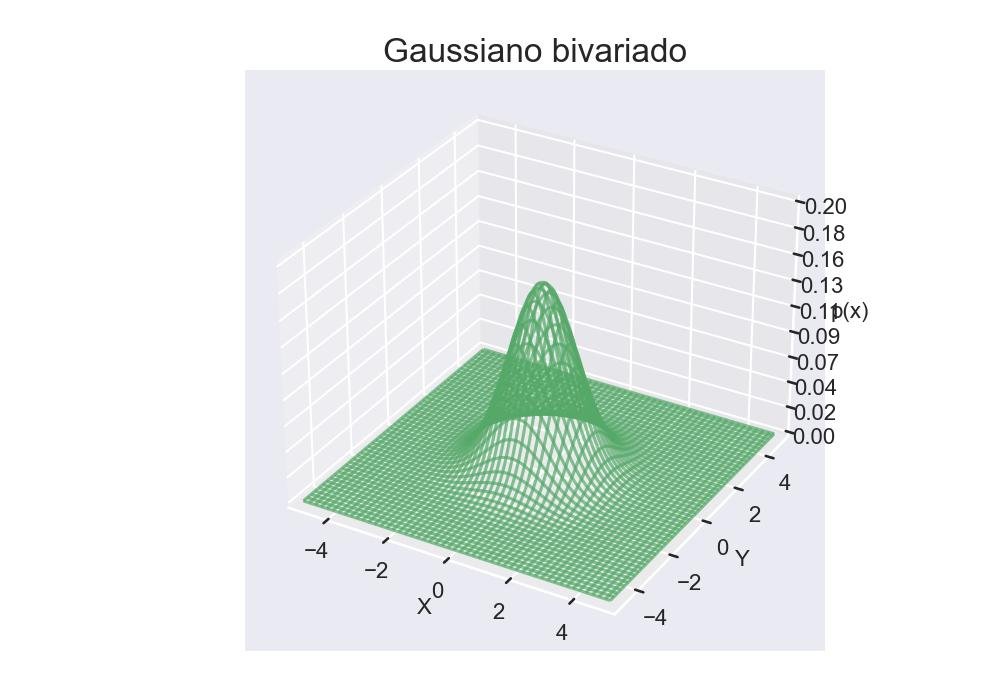

9.2 - Gráficos de barras

9.2.1 - Gráfico de barras com barras de erro

import matplotlib.pyplot as plt

# Dados de entrada
mean_values = [1, 2, 3]
variance = [0.2, 0.4, 0.5]
bar_labels = ['bar 1', 'bar 2', 'bar 3']

# barras de plotagem
x_pos = list(range(len(bar_labels)))
plt.bar(x_pos, mean_values, yerr=variance, align='center', alpha=0.5)

plt.grid()

# definir a altura do eixo y
max_y = max(zip(mean_values, variance)) # returns a tuple, here: (3, 5)
plt.ylim([0, (max_y[0] + max_y[1]) * 1.1])

# definir rótulos de eixos e título
plt.ylabel('variável y')
plt.xticks(x_pos, bar_labels)
plt.title('Gráfico de barras com barras de erro')

plt.show()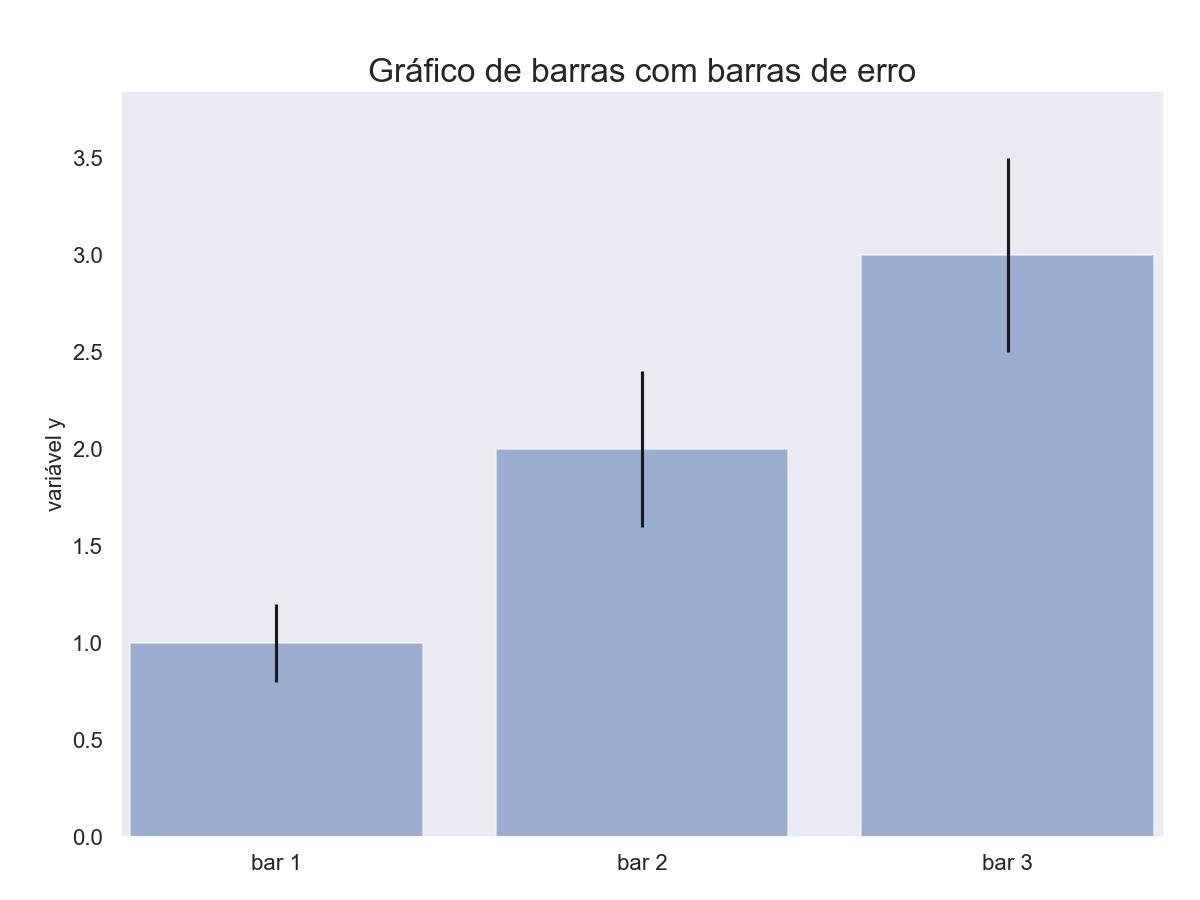

9.2.2 - Gráfico de barra horizontal com barras de erro

from matplotlib import pyplot as plt
import numpy as np

# Dados de entrada
mean_values = [1, 2, 3]
std_dev = [0.2, 0.4, 0.5]
bar_labels = ['bar 1', 'bar 2', 'bar 3']

fig = plt.figure(figsize=(8,6))

# barras de plotagem
y_pos = np.arange(len(mean_values))
y_pos = [x for x in y_pos]
plt.yticks(y_pos, bar_labels, fontsize=10)
plt.barh(y_pos, mean_values, xerr=std_dev, 
         align='center', alpha=0.4, color='g')

# anotação e rótulos
plt.xlabel('medida x')
t = plt.title('Gráfico de barras com desvio padrão')
plt.ylim([-1,len(mean_values)+0.5])
plt.xlim([0, 4])
plt.grid()

plt.show()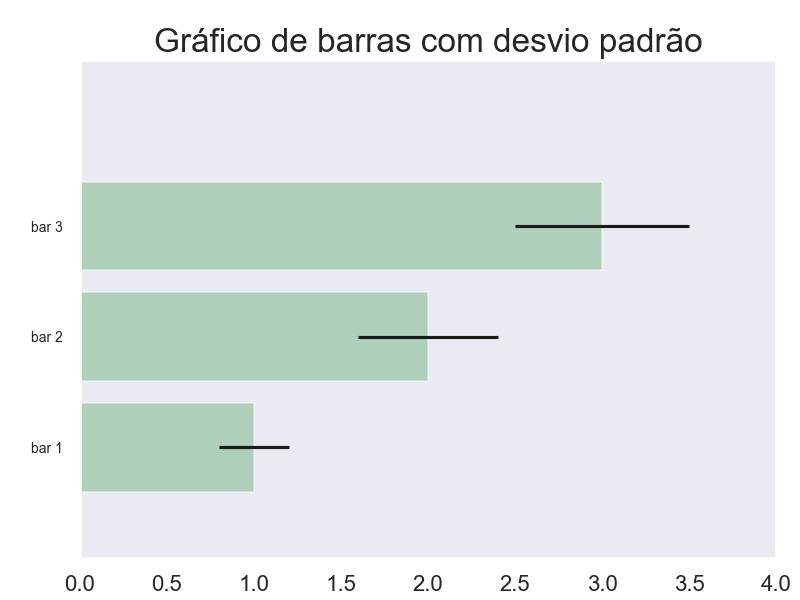

9.2.3 - Gráfico de barra back-to-back

 from matplotlib import pyplot as plt
import numpy as np

# Dados de entrada
X1 = np.array([1, 2, 3])
X2 = np.array([2, 2, 3])

bar_labels = ['bar 1', 'bar 2', 'bar 3']

fig = plt.figure(figsize=(8,6))

# barras de plotagem
y_pos = np.arange(len(X1))
y_pos = [x for x in y_pos]
plt.yticks(y_pos, bar_labels, fontsize=10)

plt.barh(y_pos, X1, 
         align='center', alpha=0.4, color='g')

# simplesmente negamos os valores do array numpy para a segunda barra

plt.barh(y_pos, -X2,
         align='center', alpha=0.4, color='b')

# anotação e rótulos
plt.xlabel('medida x')
t = plt.title('Gráfico de barras com desvio padrão')
plt.ylim([-1,len(X1)+0.1])
plt.xlim([-max(X2)-1, max(X1)+1])
plt.grid()

plt.show()

9.2.4 - gráfico de barras agrupadas

import matplotlib.pyplot as plt

# Dados de entrada
green_data = [1, 2, 3]
blue_data = [3, 2, 1]
red_data = [2, 3, 3]
labels = ['group 1', 'group 2', 'group 3']

# Definindo as posições e a largura das barras
pos = list(range(len(green_data))) 
width = 0.2 
    
# Plotando as barras
fig, ax = plt.subplots(figsize=(8,6))

plt.bar(pos, green_data, width,
    alpha=0.5, color='g', label=labels[0])

plt.bar([p + width for p in pos], blue_data, width,
    alpha=0.5, color='b', label=labels[1])
    
plt.bar([p + width*2 for p in pos], red_data, width,
    alpha=0.5, color='r', label=labels[2])

# Configurando rótulos e marcas de eixo
ax.set_ylabel('y-value')
ax.set_title('Grouped bar plot')
ax.set_xticks([p + 1.5 * width for p in pos])
ax.set_xticklabels(labels)

# Definindo os limites do eixo x e do eixo y
plt.xlim(min(pos)-width, max(pos)+width*4)
plt.ylim([0, max(green_data + blue_data + red_data) * 1.5])

# Adicionando a legenda e mostrando o gráfico
plt.legend(['green', 'blue', 'red'], loc='upper left')
plt.grid()
plt.show()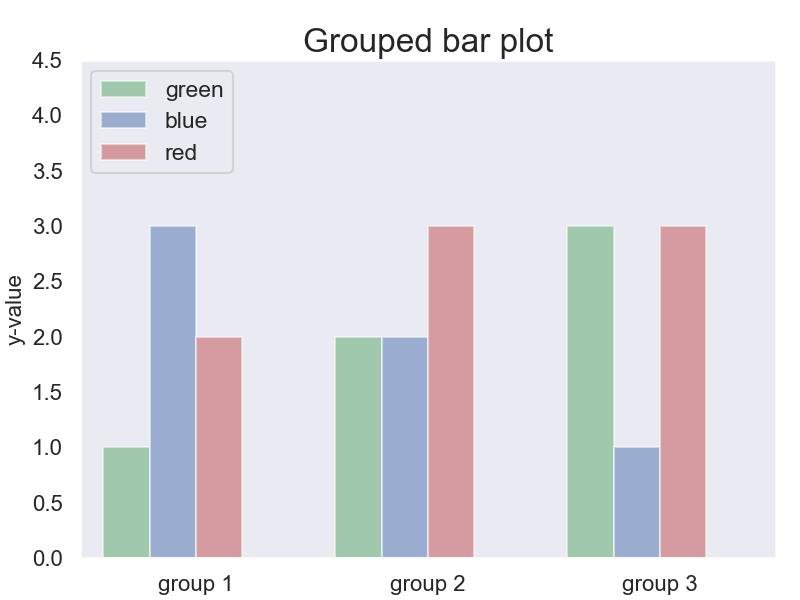

9.2.5 - Gráfico de barras empilhadas

import matplotlib.pyplot as plt

blue_data = [100,120,140]
red_data = [150,120,190]
green_data = [80,70,90]

f, (ax1, ax2) = plt.subplots(1, 2, figsize=(10,5))

bar_width = 0.5

# posições dos limites da barra esquerda
bar_l = [i+1 for i in range(len(blue_data))] 

# posições dos ticks do eixo x (centro das barras como rótulos de barras)
tick_pos = [i+(bar_width/2) for i in bar_l] 

####################
## contagem absoluta
####################

ax1.bar(bar_l, blue_data, width=bar_width,
        label='blue data', alpha=0.5, color='b')
ax1.bar(bar_l, red_data, width=bar_width,
        bottom=blue_data, label='red data', alpha=0.5, color='r')
ax1.bar(bar_l, green_data, width=bar_width,
        bottom=[i+j for i,j in zip(blue_data,red_data)], label='green data', alpha=0.5, color='g')

plt.sca(ax1)
plt.xticks(tick_pos, ['category 1', 'category 2', 'category 3'])

ax1.set_ylabel("Count")
ax1.set_xlabel("")
plt.legend(loc='upper left')
plt.xlim([min(tick_pos)-bar_width, max(tick_pos)+bar_width])
plt.grid()

# girar rótulos de eixo
plt.setp(plt.gca().get_xticklabels(), rotation=45, horizontalalignment='right')

#############
## Percentual
#############

totals = [i+j+k for i,j,k in zip(blue_data, red_data, green_data)]
blue_rel = [i / j * 100 for  i,j in zip(blue_data, totals)]
red_rel = [i / j * 100 for  i,j in zip(red_data, totals)]
green_rel = [i / j * 100 for  i,j in zip(green_data, totals)]

ax2.bar(bar_l, blue_rel, 
        label='blue data', alpha=0.5, color='b', width=bar_width
        )
ax2.bar(bar_l, red_rel, 
        bottom=blue_rel, label='red data', alpha=0.5, color='r', width=bar_width
        )
ax2.bar(bar_l, green_rel, 
        bottom=[i+j for i,j in zip(blue_rel, red_rel)], 
        label='green data', alpha=0.5, color='g', width=bar_width
        )

plt.sca(ax2)
plt.xticks(tick_pos, ['category 1', 'category 2', 'category 3'])
ax2.set_ylabel("Percentage")
ax2.set_xlabel("")

plt.xlim([min(tick_pos)-bar_width, max(tick_pos)+bar_width])
plt.grid()

# girar rótulos de eixo
plt.setp(plt.gca().get_xticklabels(), rotation=45, horizontalalignment='right')

plt.show()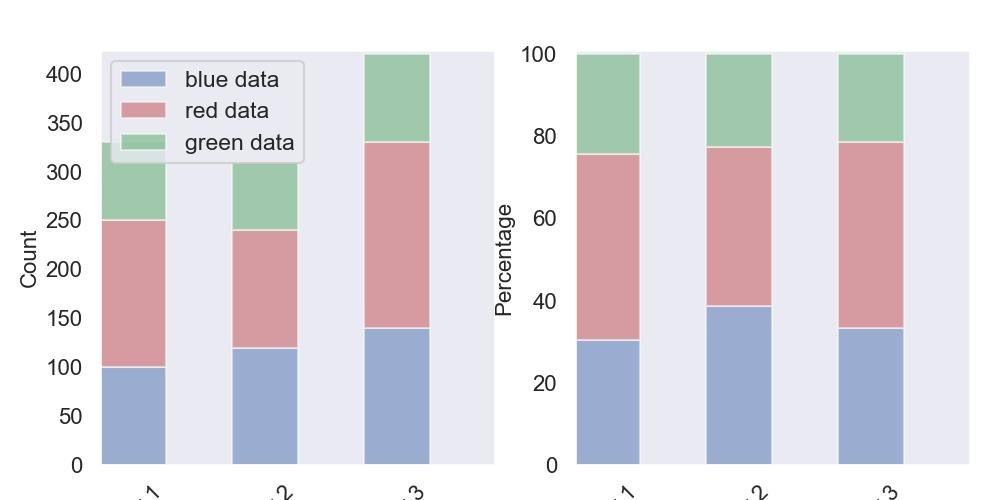

9.2.6 - Gráfico de barras com rótulos de gráfico/texto 1

from matplotlib import pyplot as plt
import numpy as np

data = range(200, 225, 5)

bar_labels = ['a', 'b', 'c', 'd', 'e']

fig = plt.figure(figsize=(10,8))

# barras de plotagem
y_pos = np.arange(len(data))
plt.yticks(y_pos, bar_labels, fontsize=16)
bars = plt.barh(y_pos, data,
         align='center', alpha=0.4, color='g')

# anotação e rótulos

for b,d in zip(bars, data):
    plt.text(b.get_width() + b.get_width()*0.08, b.get_y() + b.get_height()/2,
        '{0:.2%}'.format(d/min(data)), 
        ha='center', va='bottom', fontsize=12)

plt.xlabel('X axis label', fontsize=14)
plt.ylabel('Y axis label', fontsize=14)
t = plt.title('Gráfico de barras com rótulos/texto do gráfico', fontsize=18)
plt.ylim([-1,len(data)+0.5])
plt.vlines(min(data), -1, len(data)+0.5, linestyles='dashed')
plt.grid()

plt.show()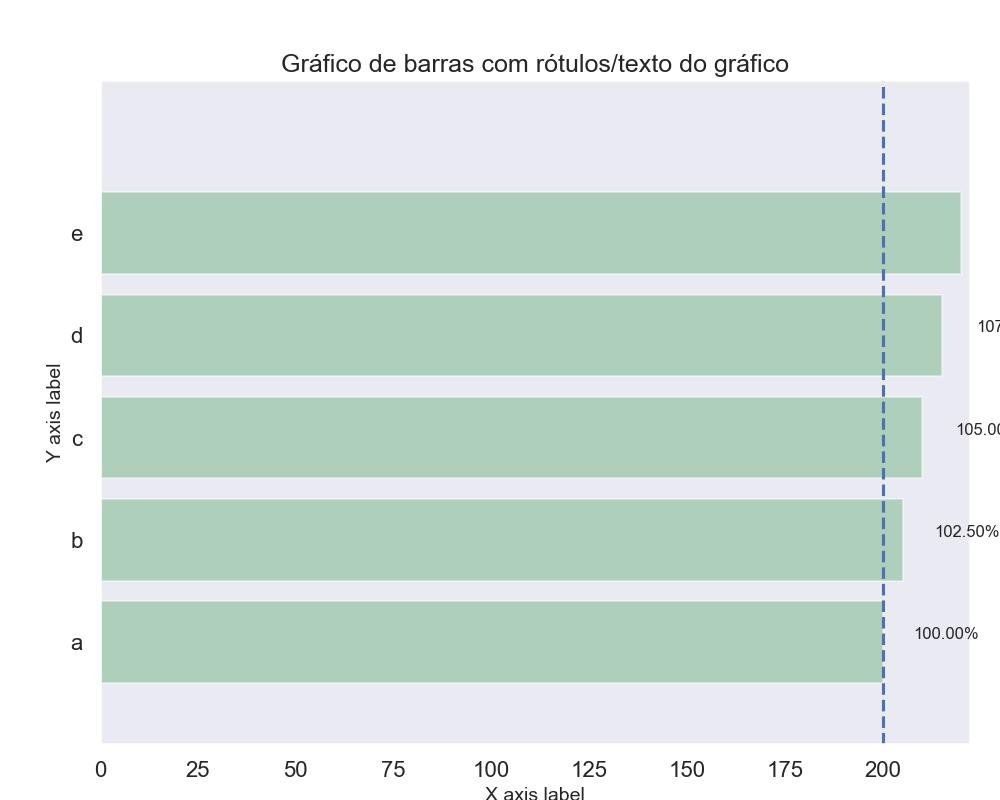

9.2.7 - Gráfico de barras com rótulos de gráfico/texto 2

import matplotlib.pyplot as plt

# Dados de entrada
mean_values = [1, 2, 3]
bar_labels = ['bar 1', 'bar 2', 'bar 3']

# barras de plotagem
x_pos = list(range(len(bar_labels)))
rects = plt.bar(x_pos, mean_values, align='center', alpha=0.5)

# barras de rótulo
def autolabel(rects):
    for ii,rect in enumerate(rects):
        height = rect.get_height()
        plt.text(rect.get_x()+rect.get_width()/2., 1.02*height, '%s'% (mean_values[ii]),
            ha='center', va='bottom')
autolabel(rects)

# definir a altura do eixo y
max_y = max(zip(mean_values, variance)) # returns a tuple, here: (3, 5)
plt.ylim([0, (max_y[0] + max_y[1]) * 1.1])

# definir rótulos de eixos e título
plt.ylabel('variável y')
plt.xticks(x_pos, bar_labels)
plt.title('Gráfico de barras com rótulos')

plt.show()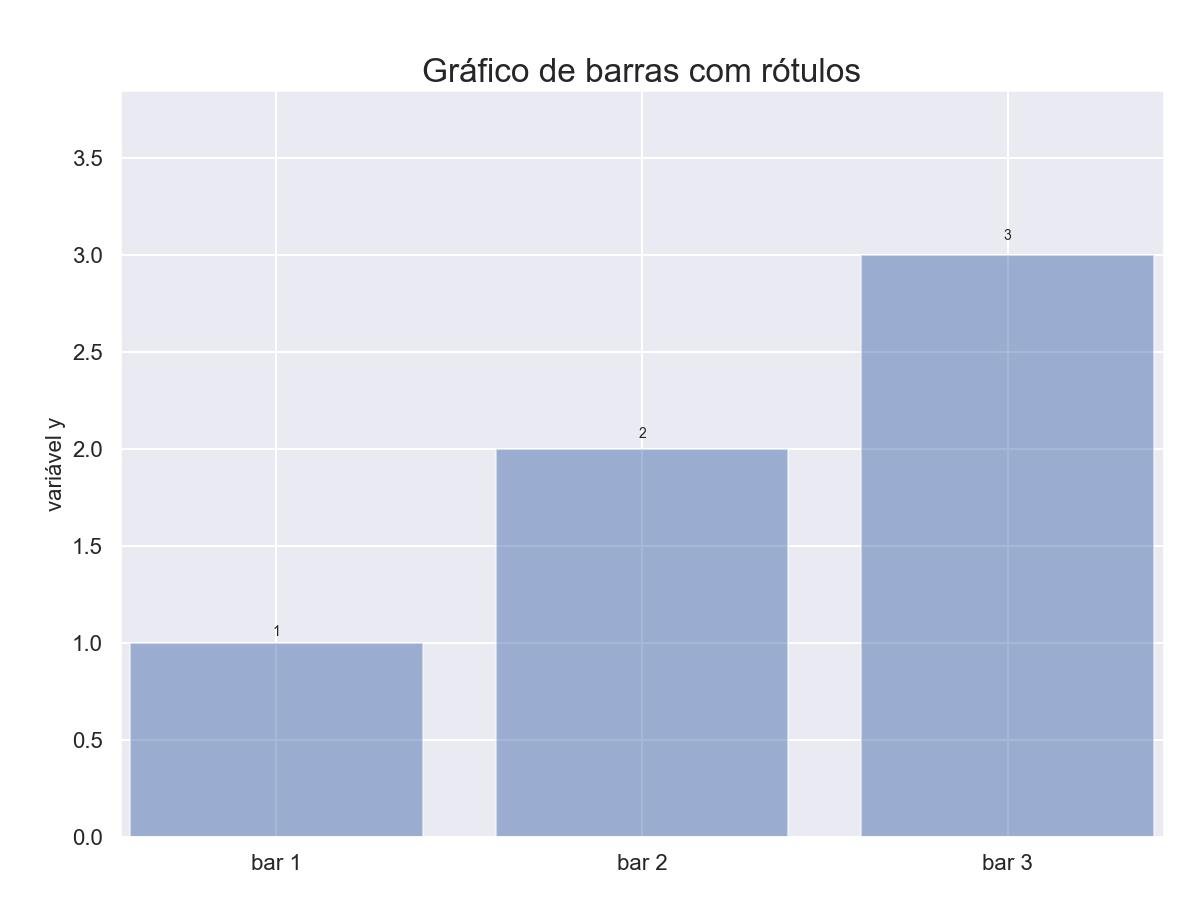

9.2.8 - Gráfico de barras com rótulos e texto com rotação automática

import matplotlib.pyplot as plt

idx = range(4)
values = [100, 1000, 5000, 20000]
labels = ['category 1', 'category 2',
          'category 3', 'category 4']

fig, ax = plt.subplots(1)

# Alinhar e girar rótulos de escala automaticamente
fig.autofmt_xdate()

bars = plt.bar(idx, values, align='center')
plt.xticks(idx, labels)
plt.tight_layout()

# Adicione rótulos de texto ao topo das barras
def autolabel(bars):
    for bar in bars:
        height = bar.get_height()
        ax.text(bar.get_x() + bar.get_width()/2., 1.05 * height,
                '%d' % int(height),
                ha='center', va='bottom')

autolabel(bars)
plt.ylim([0, 25000])
plt.show()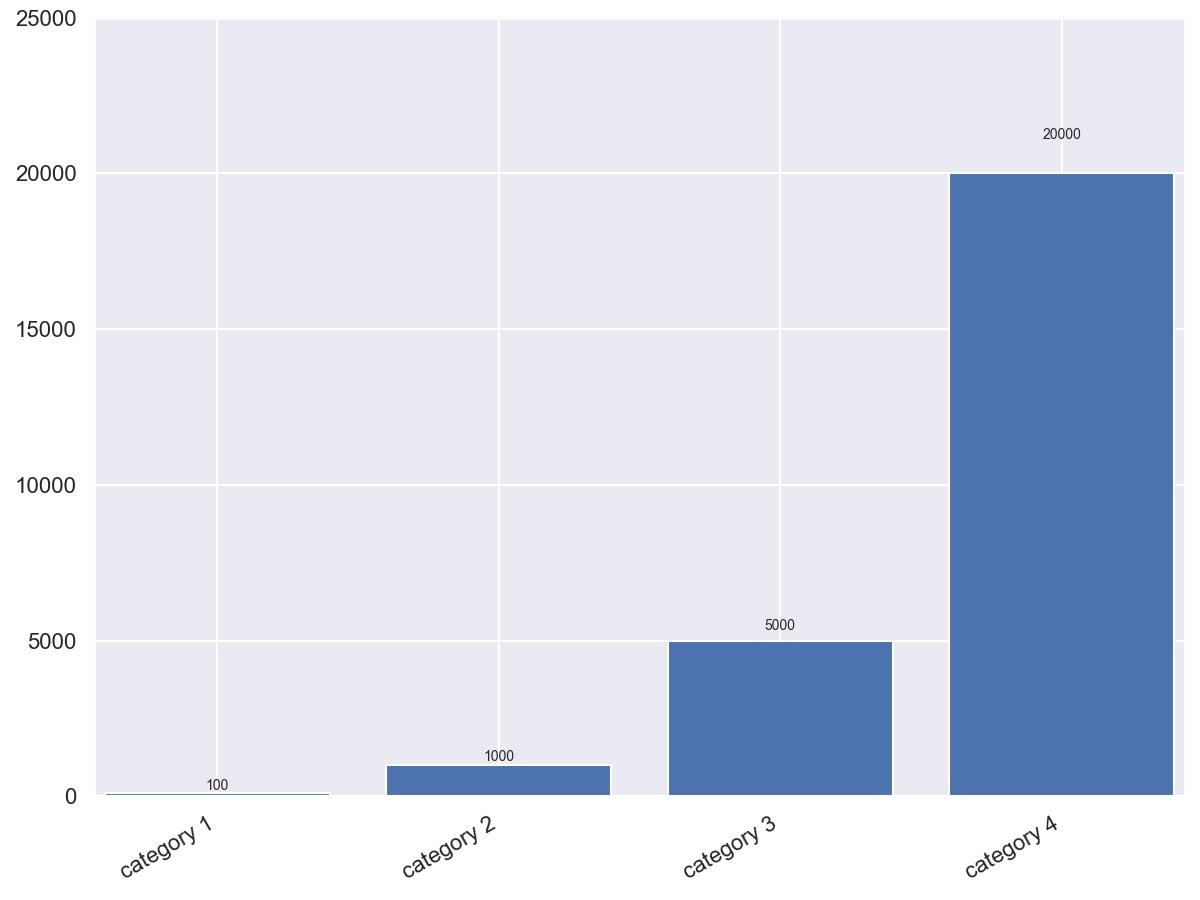

9.2.9 - Gráfico de barras com gradiente de cores

import matplotlib.pyplot as plt
import matplotlib.colors as col
import matplotlib.cm as cm

# Dados de entrada
mean_values = range(10,18)
x_pos = range(len(mean_values))

# Criar o mapa de cores
cmap1 = cm.ScalarMappable(col.Normalize(min(mean_values), max(mean_values), cm.hot))
cmap2 = cm.ScalarMappable(col.Normalize(0, 20, cm.hot))

# Barras de plotagem
plt.subplot(121)
plt.bar(x_pos, mean_values, align='center', alpha=0.5, color=cmap1.to_rgba(mean_values))
plt.ylim(0, max(mean_values) * 1.1)

plt.subplot(122)
plt.bar(x_pos, mean_values, align='center', alpha=0.5, color=cmap2.to_rgba(mean_values))
plt.ylim(0, max(mean_values) * 1.1)

plt.show()

9.2.10 - Preenchimento de padrão de plotagem de barras

import matplotlib.pyplot as plt

patterns = ('-', '+', 'x', '\\', '*', 'o', 'O', '.')

fig = plt.gca()

# Dados de entrada
mean_values = range(1, len(patterns)+1)

# barras de plotagem
x_pos = list(range(len(mean_values)))
bars = plt.bar(x_pos, 
               mean_values, 
               align='center', 
               color='white',
               )

# definir padrões
for bar, pattern in zip(bars, patterns):
     bar.set_hatch(pattern)
        
# definir rótulos de eixos e formatação
fig.axes.get_yaxis().set_visible(False)        
plt.ylim([0, max(mean_values) * 1.1])
plt.xticks(x_pos, patterns)

plt.show()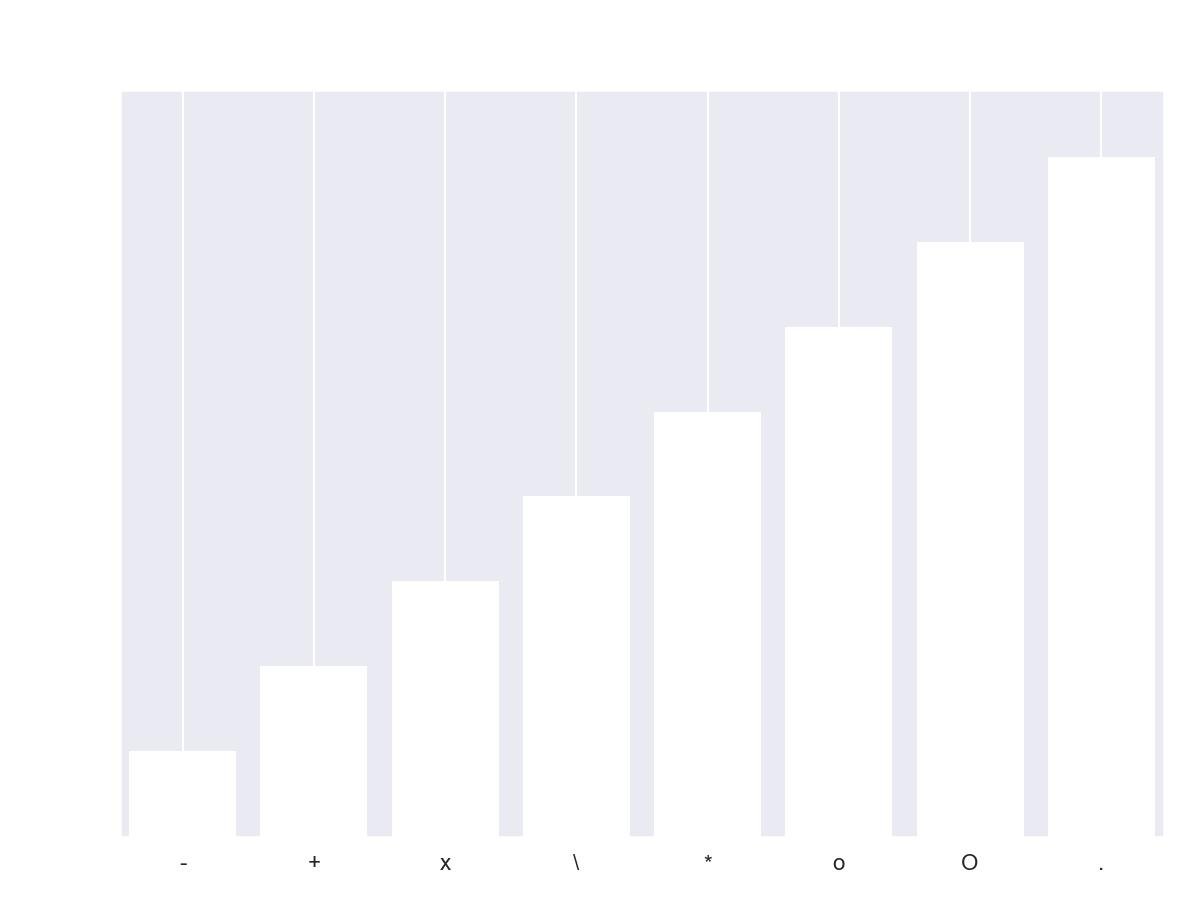

9.3 - Gráficos de caixa (boxplot)

9.3.1 - Caixa simples

import matplotlib.pyplot as plt
import numpy as np

all_data = [np.random.normal(0, std, 100) for std in range(1, 4)]

fig = plt.figure(figsize=(8,6))

plt.boxplot(all_data, 
            notch=False, # box instead of notch shape 
            sym='rs',    # red squares for outliers
            vert=True)   # vertical box aligmnent

plt.xticks([y+1 for y in range(len(all_data))], ['x1', 'x2', 'x3'])
plt.xlabel('medida x')
t = plt.title('Gráfico de caixa')
plt.show()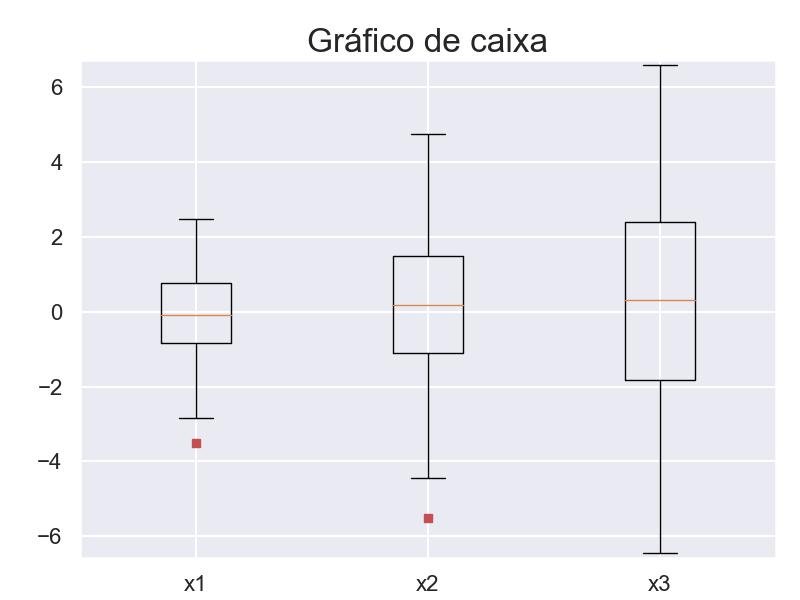

9.3.2 - Caixas preta e branca

import matplotlib.pyplot as plt
import numpy as np

all_data = [np.random.normal(0, std, 100) for std in range(1, 4)]

fig = plt.figure(figsize=(8,6))

bplot = plt.boxplot(
    all_data, 
    notch=False, # caixa em vez de forma de entalhe
    sym='rs',    # quadrados vermelhos para outliers
    vert=True)   # alinhamento vertical da caixa

plt.xticks([y+1 for y in range(len(all_data))], ['x1', 'x2', 'x3'])
plt.xlabel('medida x')

for components in bplot.keys():
    for line in bplot[components]:
        line.set_color('black')     # black lines

t = plt.title('Gráfico de caixa preto e branco')

plt.show()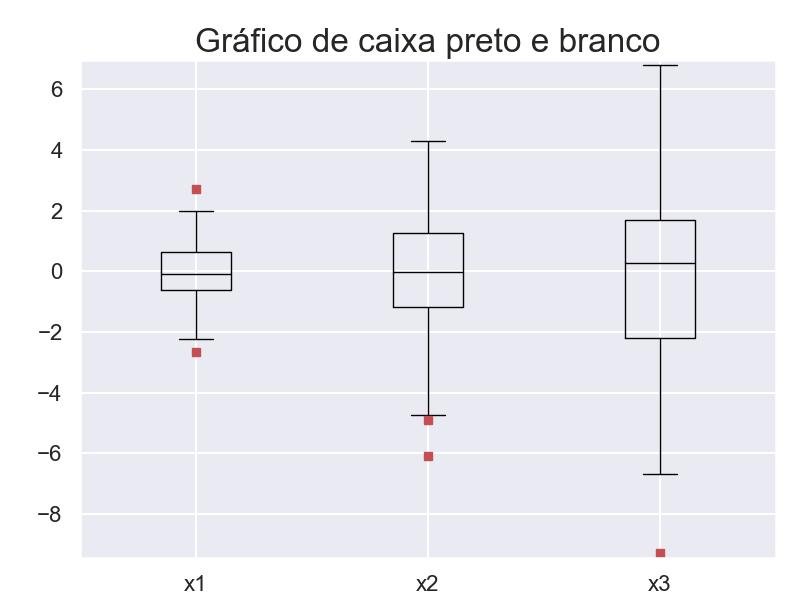

9.3.3 - Caixa horizontal

import matplotlib.pyplot as plt
import numpy as np

all_data = [np.random.normal(0, std, 100) for std in range(1, 4)]

fig = plt.figure(figsize=(8,6))

plt.boxplot(
    all_data, 
    notch=False,  # caixa em vez de forma de entalhe
    sym='rs',     # quadrados vermelhos para outliers
    vert=False)   # alinhamento de caixa horizontal

plt.yticks([y+1 for y in range(len(all_data))], ['x1', 'x2', 'x3'])
plt.ylabel('medida x')
t = plt.title('Gráfico de caixa horizontal')
plt.show()

9.3.4 - Caixa cheia e cilíndrica

import matplotlib.pyplot as plt
import numpy as np

all_data = [np.random.normal(0, std, 100) for std in range(1, 4)]

fig = plt.figure(figsize=(8,6))

plt.boxplot(
    all_data, 
    notch=True,        # forma de entalhe
    sym='bs',          # quadrados azuis para outliers
    vert=True,         # alinhamento vertical da caixa
    patch_artist=True) # preencher com cor

plt.xticks([y+1 for y in range(len(all_data))], ['x1', 'x2', 'x3'])
plt.xlabel('medida x')
t = plt.title('Gráfico de caixa')
plt.show()

9.3.5 - Boxplots com cores de preenchimento personalizadas

import matplotlib.pyplot as plt
import numpy as np

all_data = [np.random.normal(0, std, 100) for std in range(1, 4)]

fig = plt.figure(figsize=(8,6))

bplot = plt.boxplot(
    all_data, 
    notch=False,       # forma de entalhe
    vert=True,         # alinhamento vertical da caixa
    patch_artist=True) # preencher com cor

colors = ['pink', 'lightblue', 'lightgreen']
for patch, color in zip(bplot['boxes'], colors):
    patch.set_facecolor(color)

plt.xticks([y+1 for y in range(len(all_data))], ['x1', 'x2', 'x3'])
plt.xlabel('medida x')
t = plt.title('Gráfico de caixa')
plt.show()

9.3.6 - Caixa e barras de violino

Os gráficos de violino estão intimamente relacionados aos gráficos de caixa de Tukey (1977), mas adicionam informações úteis, como a distribuição dos dados da amostra (traço de densidade).

import matplotlib.pyplot as plt
import numpy as np

fig, axes = plt.subplots(nrows=1,ncols=2, figsize=(12,5))

all_data = [np.random.normal(0, std, 100) for std in range(6, 10)]

#fig = plt.figure(figsize=(8,6))

axes[0].violinplot(
    all_data,
    showmeans=False,
    showmedians=True 
)
axes[0].set_title('violin plot')

axes[1].boxplot(all_data,
               )
axes[1].set_title('box plot')

# adicionando linhas de grade horizontais
for ax in axes:
    ax.yaxis.grid(True) 
    ax.set_xticks([y+1 for y in range(len(all_data))], )
    ax.set_xlabel('x etiqueta')
    ax.set_ylabel('y etiqueta')

plt.setp(
    axes, xticks=[y+1 for y in range(len(all_data))], 
    xticklabels=['x1', 'x2', 'x3', 'x4'],
)    
    
plt.show()

9.4 - Gráficos de barras de erros

9.4.1 - Desvio padrão, erro padrão e intervalos de confiança

import numpy as np
from matplotlib import pyplot as plt
from scipy.stats import t

# Gerando 15 pontos de dados aleatórios no intervalo 5-15 (inclusive)
X = np.random.randint(5, 15, 15)

# sample size
n = X.size

# mean
X_mean = np.mean(X)

# desvio padrão
X_std = np.std(X)

# erro padrão
X_se = X_std / np.sqrt(n)
# alternatively:
#    from scipy import stats
#    stats.sem(X)

# Intervalo de confiança de 95%
dof = n - 1         # graus de liberdade
alpha = 1.0 - 0.95
conf_interval = t.ppf(1-alpha/2., dof) * X_std*np.sqrt(1.+1./n)

fig = plt.gca()
plt.errorbar(1, X_mean, yerr=X_std, fmt='-o')
plt.errorbar(2, X_mean, yerr=X_se, fmt='-o')
plt.errorbar(3, X_mean, yerr=conf_interval, fmt='-o')

plt.xlim([0,4])
plt.ylim(X_mean-conf_interval-2, X_mean+conf_interval+2)

# formatação de eixo
fig.axes.get_xaxis().set_visible(False)
fig.spines["top"].set_visible(False)  
fig.spines["right"].set_visible(False)  
plt.tick_params(
    axis="both", which="both", bottom="off", top="off",  
    labelbottom="on", left="on", right="off", labelleft="on")  

plt.legend(
    ['Desvio padrão', 'Erro padrão', 'Intervalo de confiança'], 
    loc='upper left',
    numpoints=1,
    fancybox=True)

plt.ylabel('variável aleatória')
plt.title('15 valores aleatórios no intervalo 5-15')

plt.show()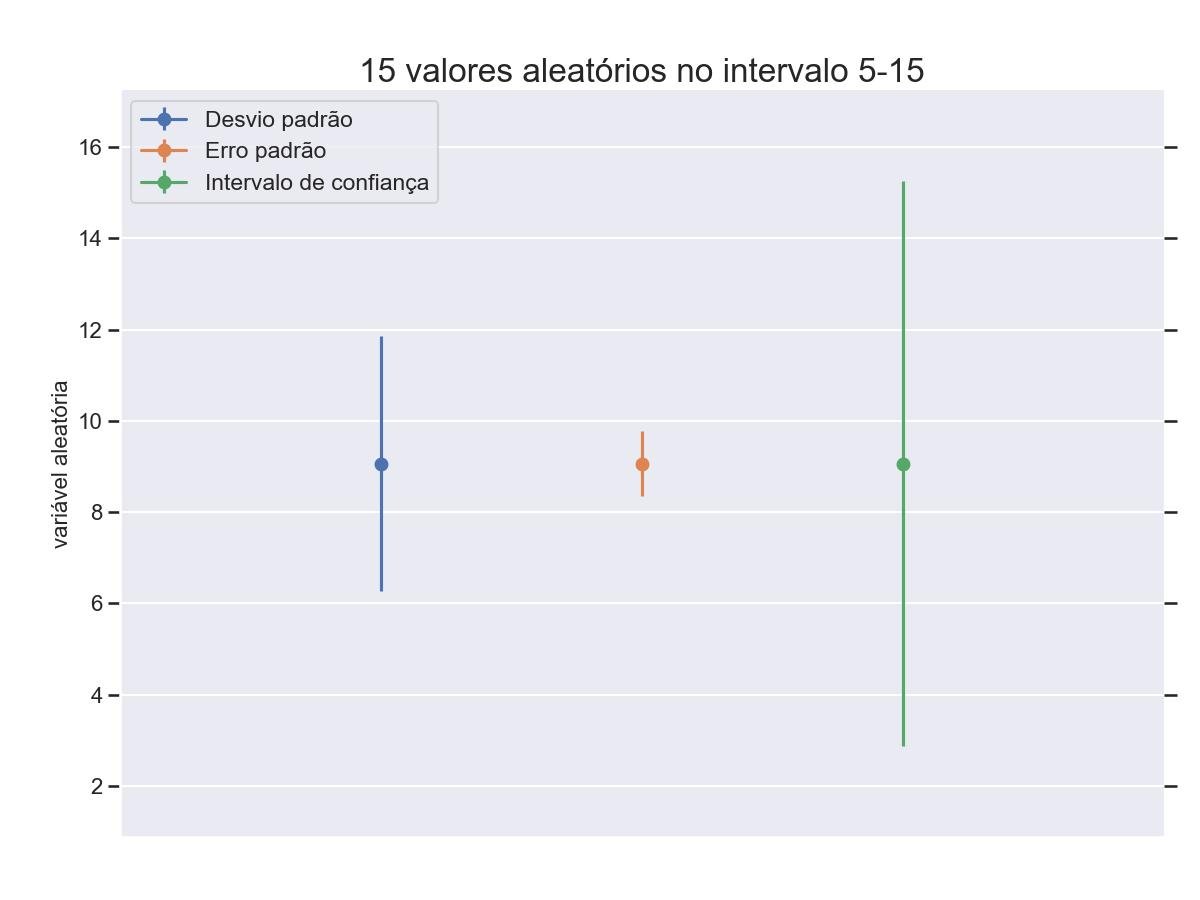

9.4.2 - Adicionando barras de erro a um barplot

import matplotlib.pyplot as plt

# Dados de entrada
mean_values = [1, 2, 3]
variance = [0.2, 0.4, 0.5]
bar_labels = ['bar 1', 'bar 2', 'bar 3']

fig = plt.gca()

# barras de plotagem
x_pos = list(range(len(bar_labels)))
plt.bar(x_pos, mean_values, yerr=variance, align='center', alpha=0.5)

# definir a altura do eixo y
max_y = max(zip(mean_values, variance)) # returns a tuple, here: (3, 5)
plt.ylim([0, (max_y[0] + max_y[1]) * 1.1])

# definir rótulos de eixos e título
plt.ylabel('variável y')
plt.xticks(x_pos, bar_labels)
plt.title('Gráfico de barras com barras de erro')

# formatação de eixo
fig.axes.get_xaxis().set_visible(False)
fig.spines["top"].set_visible(False)  
fig.spines["right"].set_visible(False)  
plt.tick_params(
    axis="both", which="both", bottom="off", top="off",  
    labelbottom="on", left="on", right="off", labelleft="on")  

plt.show()

9.5 - Formatação de gráficos

9.5.1 - subplots (subtramas)

import numpy as np
import matplotlib.pyplot as plt

x = range(10)
y = range(10)
fig, ax = plt.subplots(2)
for sp in ax: sp.plot(x, y)
plt.show()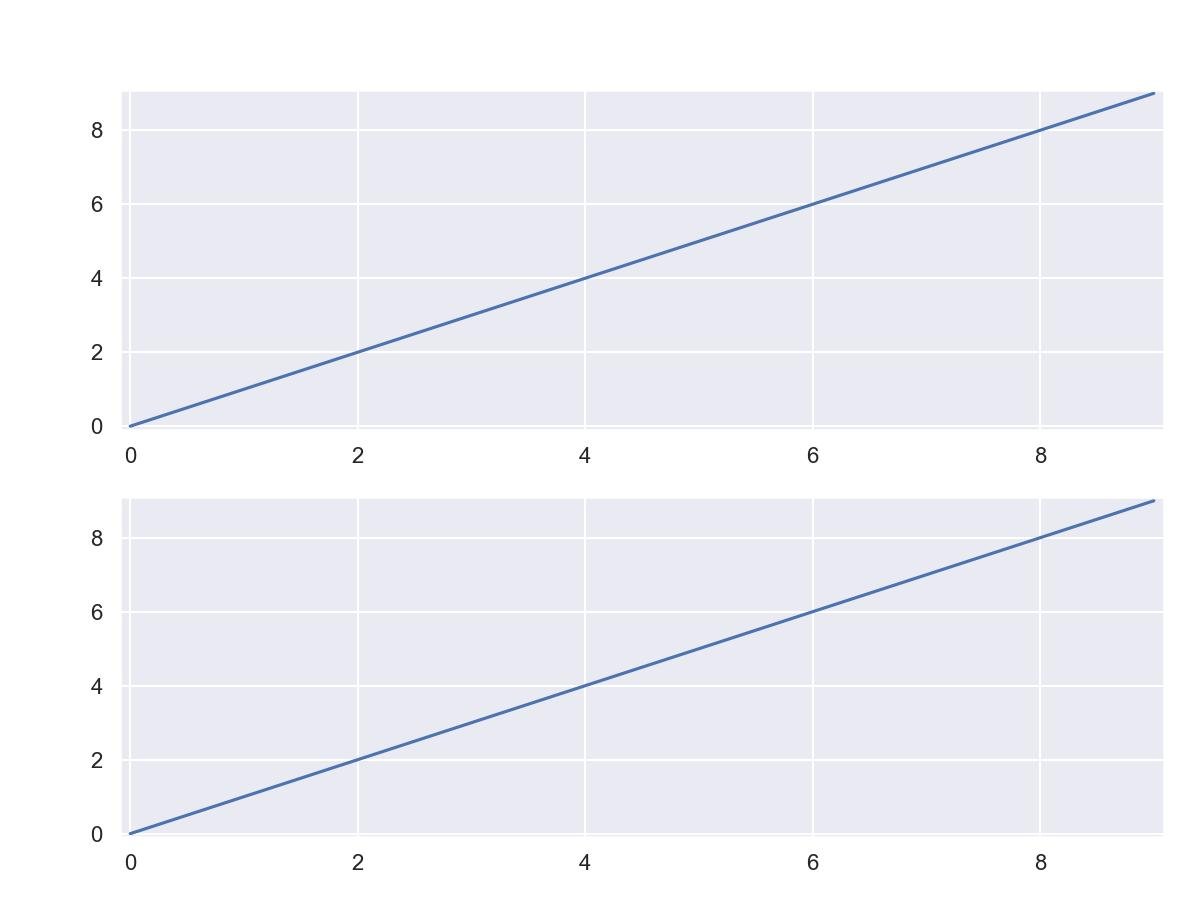

m x n subplots:

import matplotlib.pyplot as plt

x = range(10)
y = range(10)

fig, ax = plt.subplots(nrows=2,ncols=2)

for row in ax:
    for col in row:
        col.plot(x, y)
        
plt.show()

fig, ax = plt.subplots(nrows=2,ncols=2)

plt.subplot(2,2,1)
plt.plot(x, y)

plt.subplot(2,2,2)
plt.plot(x, y)
    
plt.subplot(2,2,3)
plt.plot(x, y)

plt.subplot(2,2,4)
plt.plot(x, y)
    
plt.show()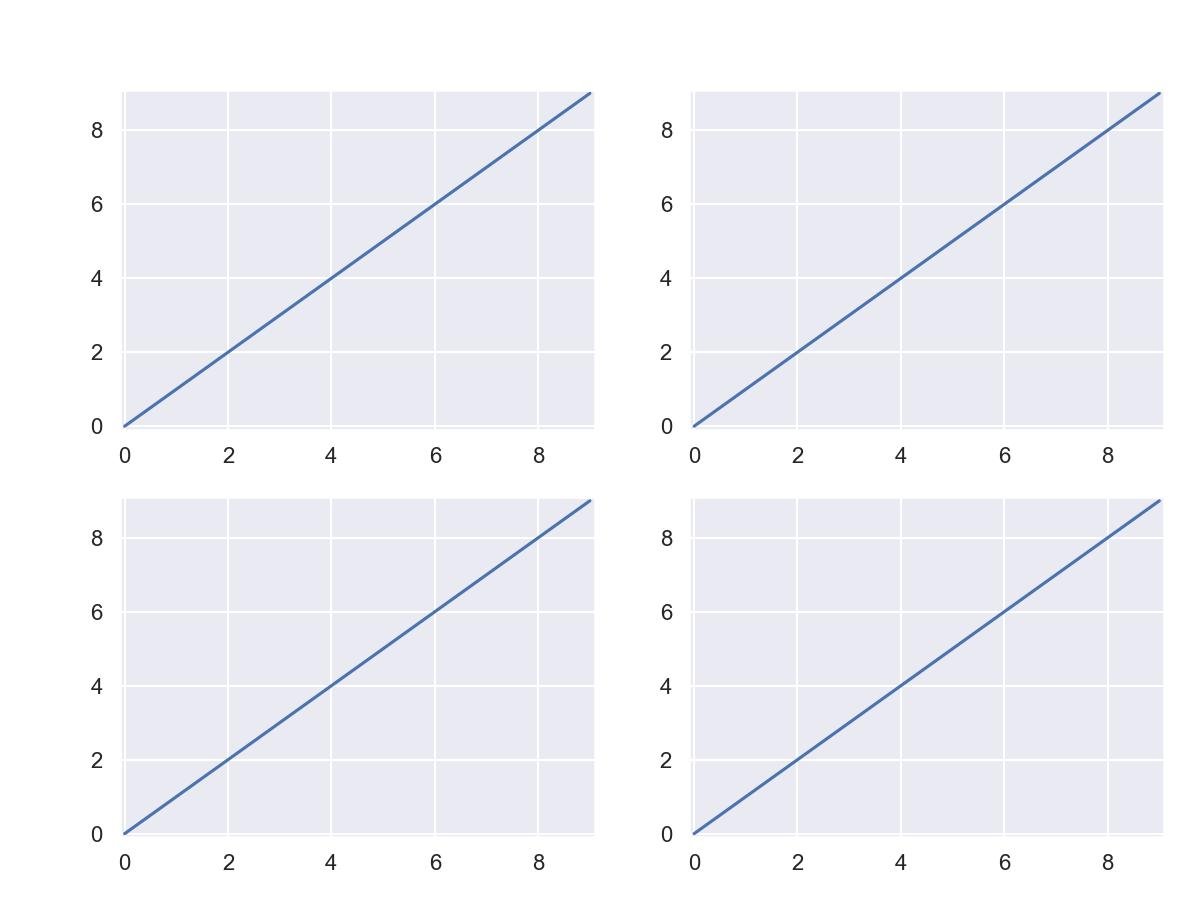

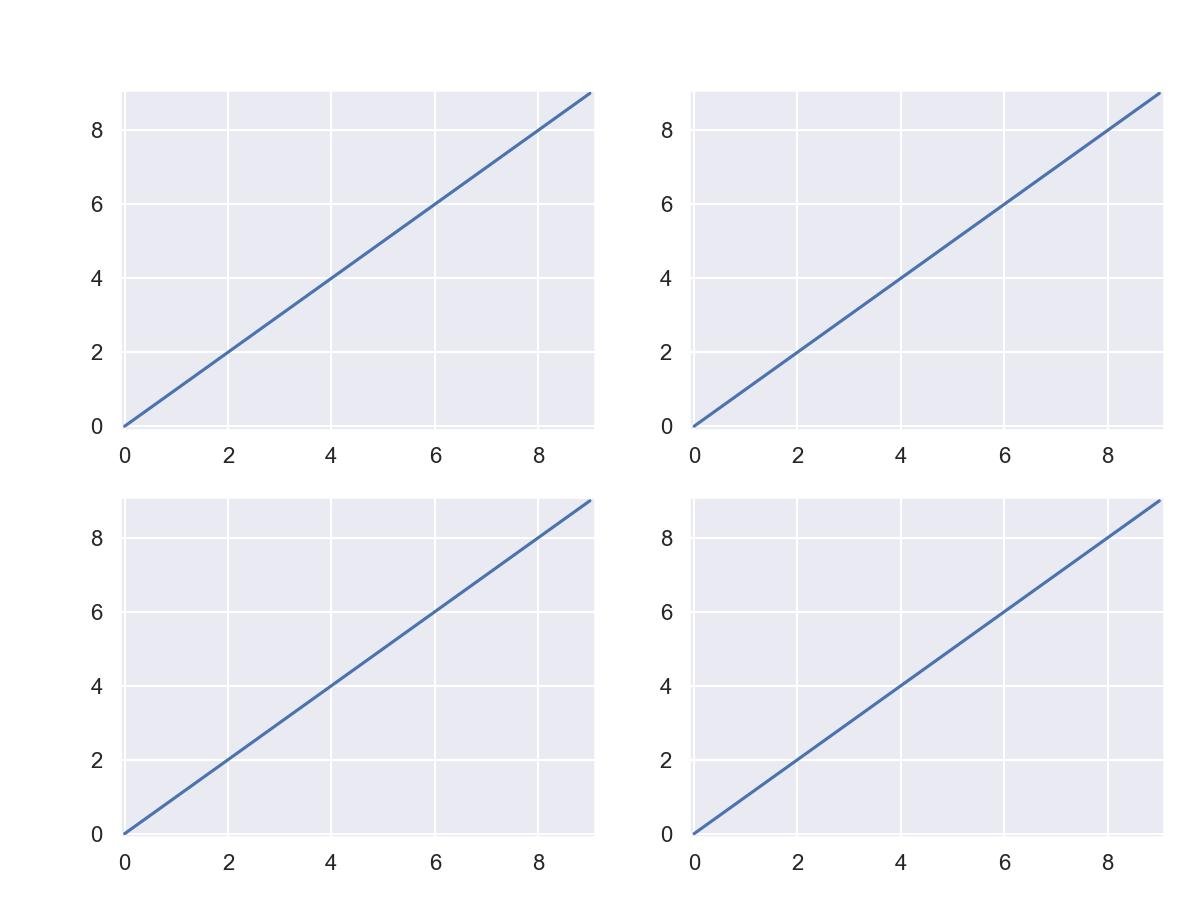
Rotular uma grade de subtrama como uma matriz:

import matplotlib.pyplot as plt
import numpy as np

fig, axes = plt.subplots(
    nrows=3, ncols=3, 
    sharex=True, sharey=True,
    figsize=(8,8)
)

x = range(5)
y = range(5)

for row in axes:
    for col in row:
        col.plot(x, y)

for ax, col in zip(axes[0,:], ['1', '2', '3']):
    ax.set_title(col, size=20)
    
for ax, row in zip(axes[:,0], ['A', 'B', 'C']):
    ax.set_ylabel(row, size=20, rotation=0, labelpad=15)
  
plt.show()

Eixos X e Y compartilhados:

import matplotlib.pyplot as plt

x = range(10)
y = range(10)

fig, ax = plt.subplots(nrows=2,ncols=2, sharex=True, sharey=True)

for row in ax:
    for col in row:
        col.plot(x, y)
    
plt.show()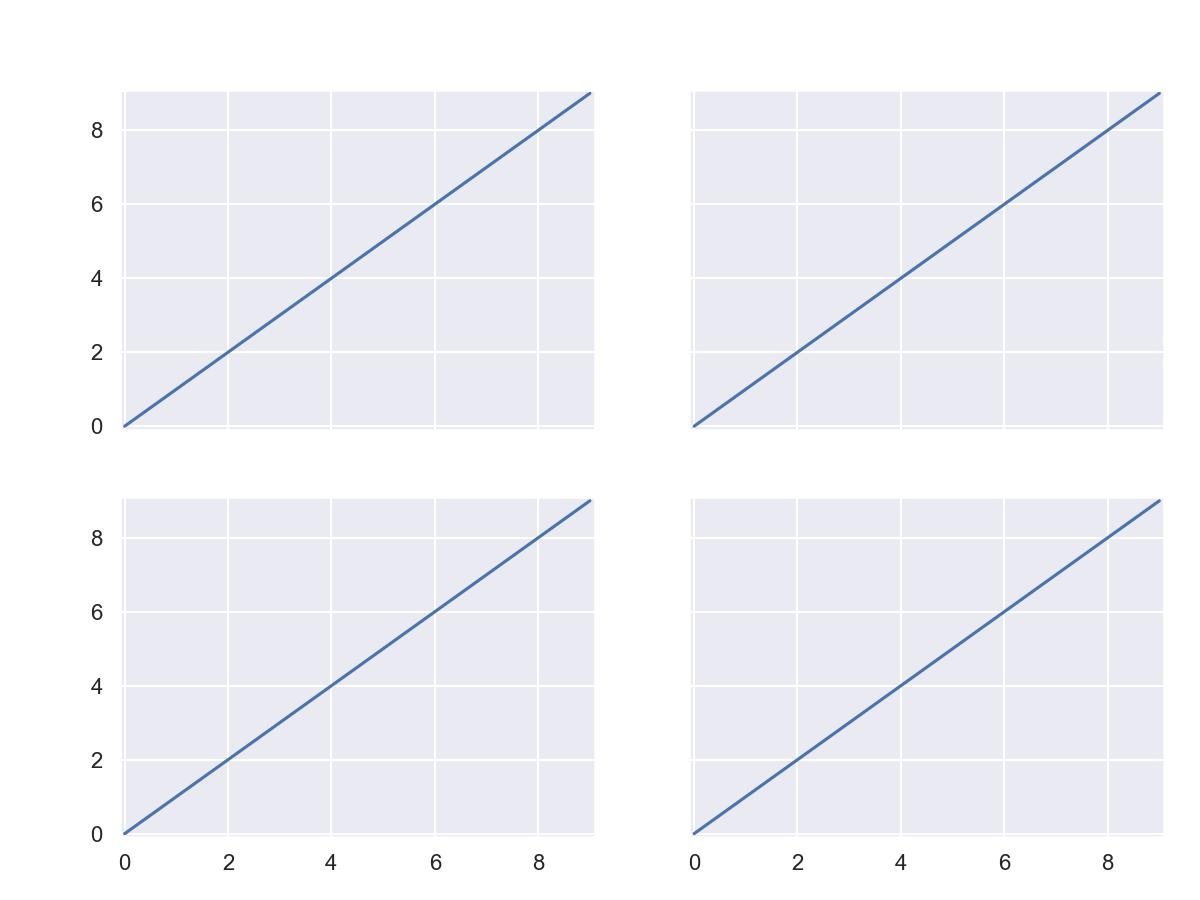

Definindo título e rótulos:

import matplotlib.pyplot as plt

x = range(10)
y = range(10)

fig, ax = plt.subplots(nrows=2,ncols=2)

for row in ax:
    for col in row:
        col.plot(x, y)
        col.set_title('título')  
        col.set_xlabel('x-axis')
        col.set_ylabel('x-axis')
                
fig.tight_layout()
            
plt.show()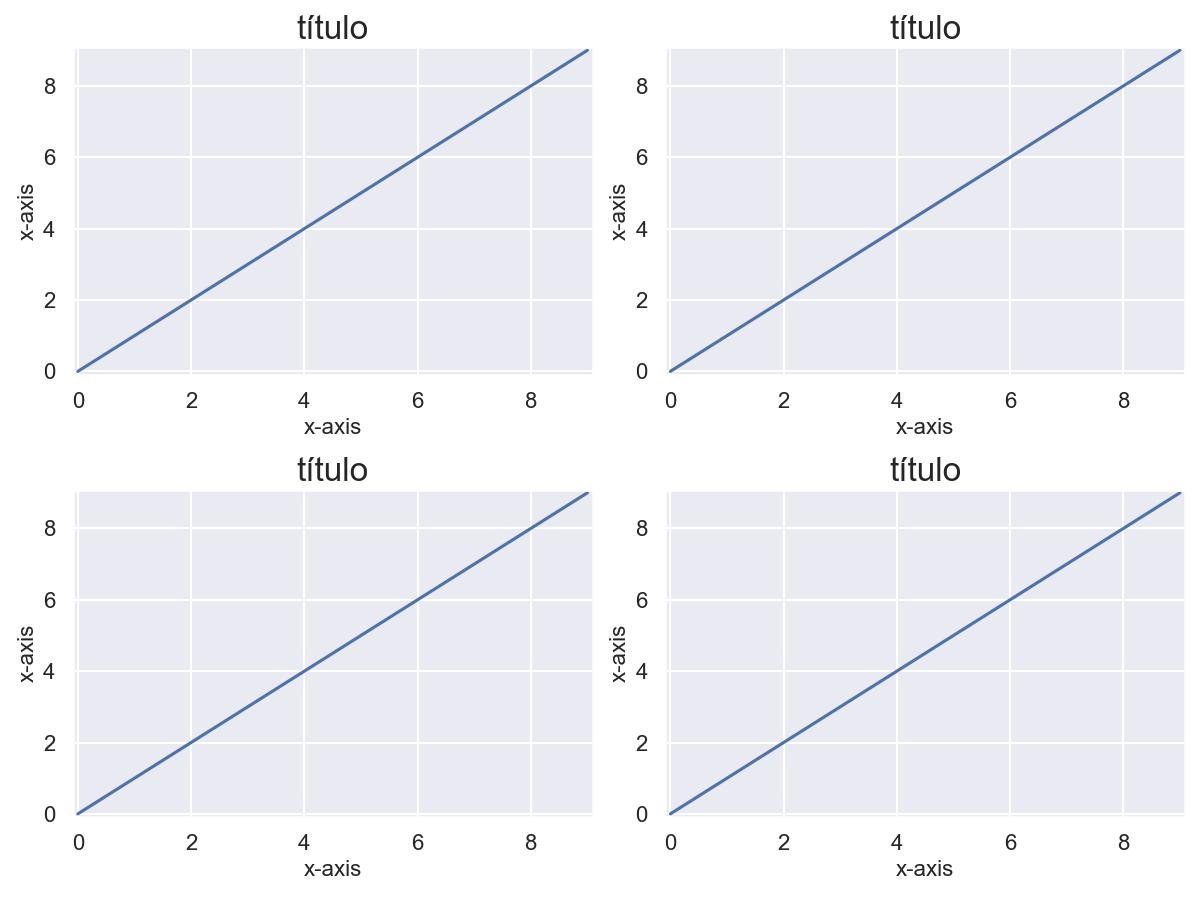

Ocultando subtramas redundantes:

Às vezes, criamos mais subparcelas para um layout retangular (aqui: 3x3) do que realmente precisamos. Aqui está como ocultamos essas subtramas redundantes. Vamos supor que queremos mostrar apenas as 7 primeiras subparcelas.

import matplotlib.pyplot as plt

x = range(10)
y = range(10)

fig, axes = plt.subplots(nrows=3,ncols=3)

for cnt, ax in enumerate(axes.ravel()):
    if cnt < 7:    
        ax.plot(x, y)
    else:
        ax.axis('off') # hide subplot
plt.show()

9.5.2 - Definindo cores

Maneiras d declaração de cores:

Matplotlib suporta 3 maneiras diferentes de codificar cores, por exemplo, se quisermos usar a cor azul, podemos definir as cores como:

Valores de cores RGB (intervalo de 0,0 a 1,0) -> (0,0, 0,0, 1,0)
nomes suportados pelo matplotlib -> 'blue' ou 'b'
Valores hexadecimais HTML -> '#0000FF'

import matplotlib.pyplot as plt

amostras = range(1,4)

for i, col in zip(amostras, [(0.0, 0.0, 1.0), 'blue', '#0000FF']):
    plt.plot([0, 10], [0, i], lw=3, color=col) 

plt.legend(
    ['valores RGB: (0.0, 0.0, 1.0)', 
    "nomes matplotlib: 'blue'", 
    "valores hex HTML: '#0000FF'"],
    loc='upper left')
plt.title('3 alternativas para definir a cor azul')

plt.show()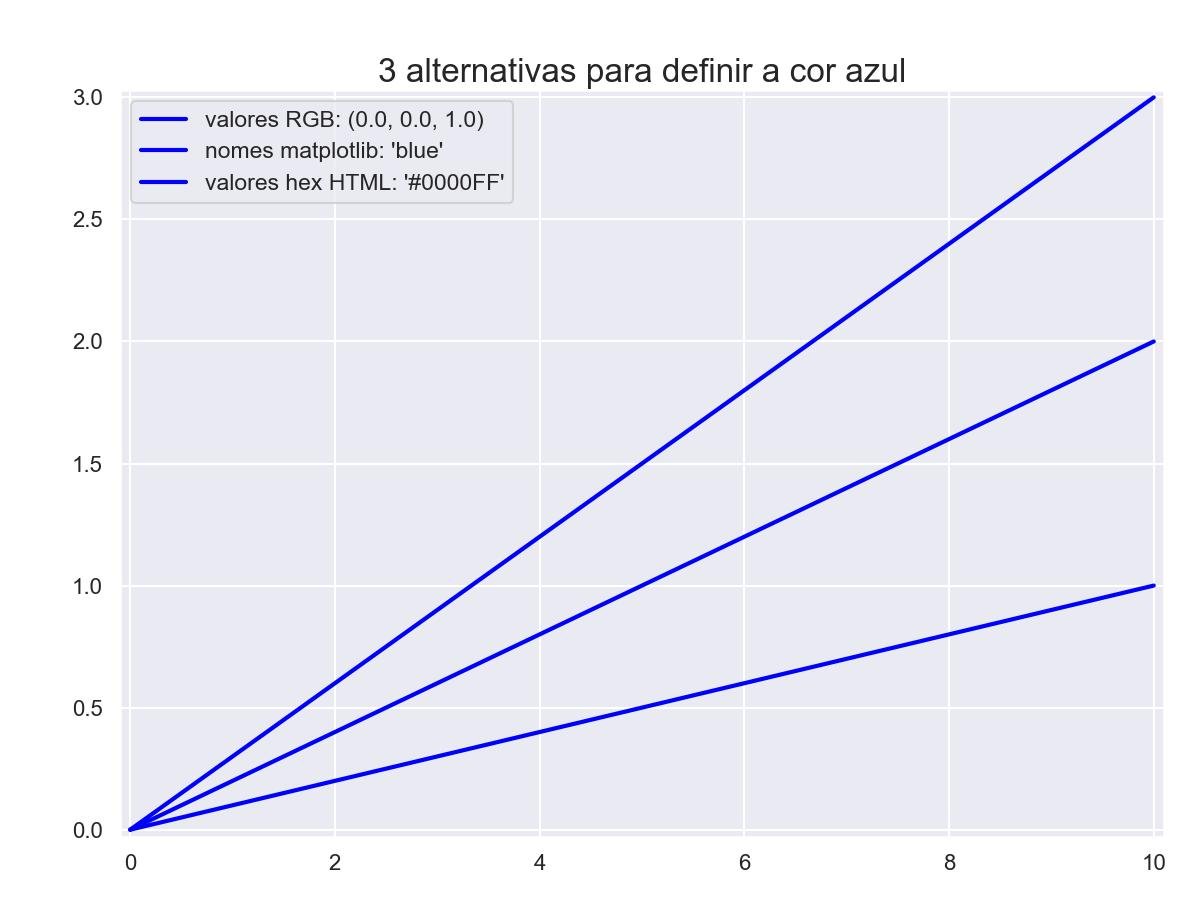

nomes de cores:

Os nomes de cores que são suportados pelo matplotlib são

b: blue (azul)

g: green (verde)

r: red (vermelho)

c: cyan (ciano)

m: magenta (magenta)

y: yellow (yellow)

k: black (black)

w: white (white)

onde a primeira letra representa a versão do atalho.

import matplotlib.pyplot as plt

cols = ['blue', 'green', 'red', 'cyan',  'magenta', 'yellow', 'black', 'white']

amostras = range(1, len(cols)+1)

for i, col in zip(amostras, cols):
    plt.plot([0, 10], [0, i], label=col, lw=3, color=col) 

plt.legend(loc='upper left')    
plt.title('nomes de cores matplotlib')
    
plt.show()

Mapas de cores:

Mais mapas de cores estão disponíveis em Scipy - Mapas de cores.

import numpy as np
import matplotlib.pyplot as plt

fig, (ax0, ax1) = plt.subplots(1,2, figsize=(14, 7))
amostras = range(1,16)

# Ciclo de cores padrão

for i in amostras:
    ax0.plot([0, 10], [0, i], label=i, lw=3) 

# Mapa de cores    
    
colormap = plt.cm.Paired
plt.gca().set_prop_cycle(color=[colormap(i) for i in np.linspace(0, 0.9, len(amostras))])

for i in amostras:
    ax1.plot([0, 10], [0, i], label=i, lw=3) 
    
# Anotações 
    
ax0.set_title('Ciclo de cores padrão')
ax1.set_title('Mapa de cores plt.cm.Paired')
ax0.legend(loc='upper left')
ax1.legend(loc='upper left')

plt.show()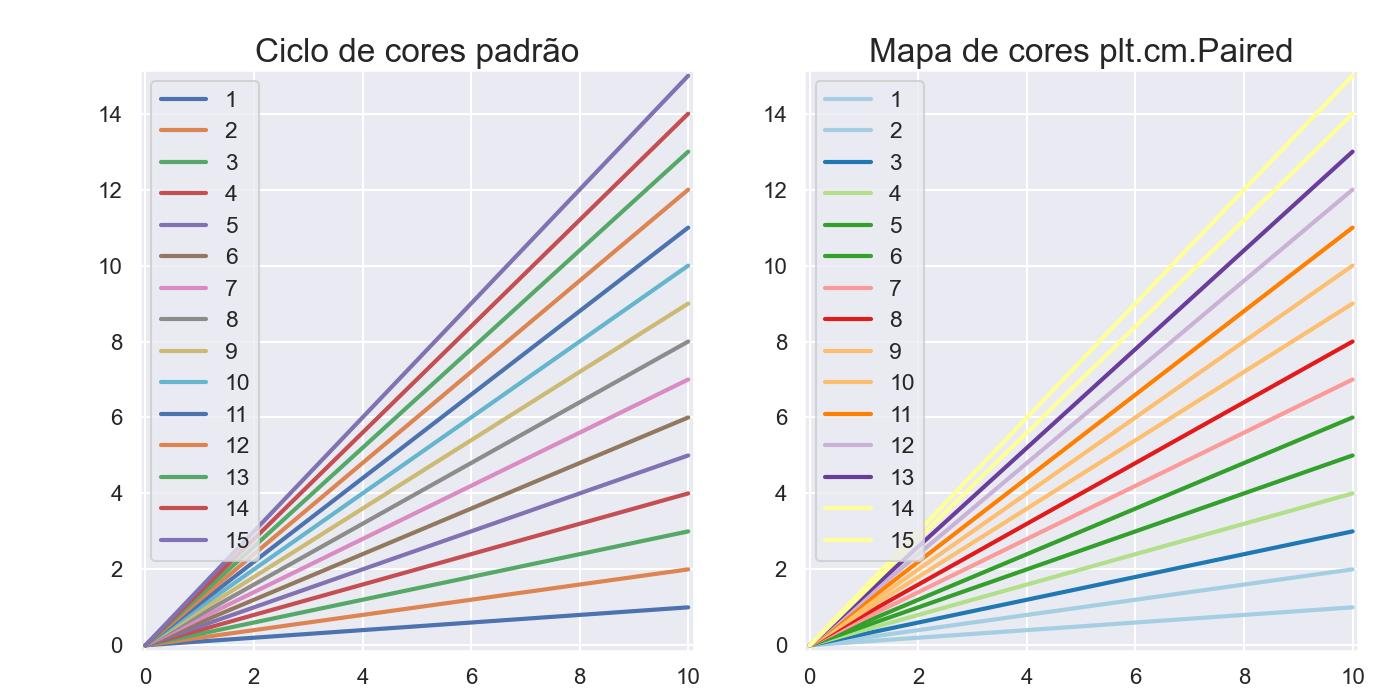

Níveis de cinza:

import matplotlib.pyplot as plt
import numpy as np

plt.figure(figsize=(8,6))

amostras = np.arange(0, 1.1, 0.1)

for i in amostras:
    # ! o nível de cinza deve ser analisado como string
    plt.plot(
        [0, 10], [0, i],
        label='gray-level %s'%i, lw=3, color=str(i))

plt.legend(loc='upper left')    
plt.title('níveis de cinza')
    
plt.show()

Cores de borda para gráficos de dispersão:

import matplotlib.pyplot as plt
import numpy as np

fig, ax = plt.subplots(nrows=2, ncols=2, figsize=(10,10))

amostras = np.random.randn(30,2)

ax[0][0].scatter(
    amostras[:,0], amostras[:,1], 
    color='red',label='color="red"')
    
ax[1][0].scatter(
    amostras[:,0], amostras[:,1],
    c='red',label='c="red"')

ax[0][1].scatter(amostras[:,0], amostras[:,1], 
            edgecolor='white', 
            c='red',
            label='c="red", edgecolor="white"')

ax[1][1].scatter(amostras[:,0], amostras[:,1], 
            edgecolor='0', 
            c='1',
            label='color="1.0", edgecolor="0"')

for row in ax:
    for col in row:
        col.legend(loc='upper left') 
    
plt.show()

Gradientes de cor:

import matplotlib.pyplot as plt
import matplotlib.colors as col
import matplotlib.cm as cm
import numpy as np

# Dados de entrada
mean_values = np.random.randint(1, 101, 100)
x_pos = range(len(mean_values))

fig = plt.figure(figsize=(20,5))

# Criar mapa de cores
cmap = cm.ScalarMappable(
    col.Normalize(min(mean_values), 
    max(mean_values), cm.hot))

# barras de plotagem

plt.subplot(131)
plt.bar(
    x_pos, mean_values, align='center', alpha=0.5, 
    color=cmap.to_rgba(mean_values))
plt.ylim(0, max(mean_values) * 1.1)

plt.subplot(132)
plt.bar(
    x_pos, np.sort(mean_values), align='center', alpha=0.5, 
    color=cmap.to_rgba(mean_values))
plt.ylim(0, max(mean_values) * 1.1)

plt.subplot(133)
plt.bar(
    x_pos, np.sort(mean_values), align='center', alpha=0.5, 
    color=cmap.to_rgba(np.sort(mean_values)))
plt.ylim(0, max(mean_values) * 1.1)

plt.show()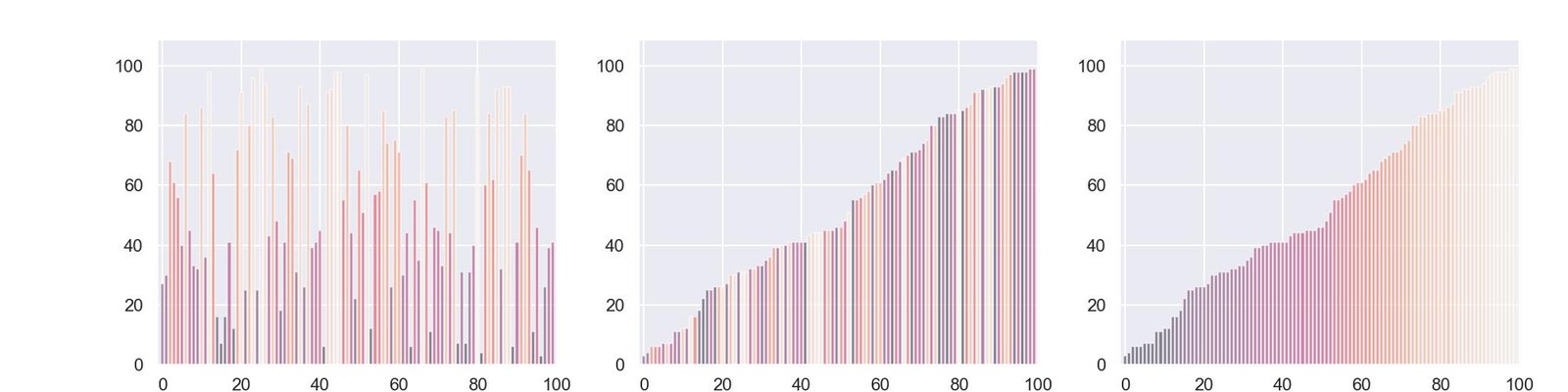

9.5.3 - Estilos de marcadores

import matplotlib.pyplot as plt

import numpy as np
import matplotlib.pyplot as plt

marcadores = [

'.', # point
',', # pixel
'o', # circle
'v', # triangle down
'^', # triangle up
'<', # triangle_left
'>', # triangle_right
'1', # tri_down
'2', # tri_up
'3', # tri_left
'4', # tri_right
'8', # octagon
's', # square
'p', # pentagon
'*', # star
'h', # hexagon1
'H', # hexagon2
'+', # plus
'x', # x
'D', # diamond
'd', # thin_diamond
'|', # vline

]

plt.figure(figsize=(13, 10))
amostras = range(len(marcadores))

for i in amostras:
    plt.plot([i-1, i, i+1], [i, i, i], label=marcadores[i], marker=marcadores[i], markersize=10) 

# Anotações 
    
plt.title('Estilos do marcador Matplotlib', fontsize=20)
plt.ylim([-1, len(marcadores)+1])
plt.legend(loc='lower right')

plt.show()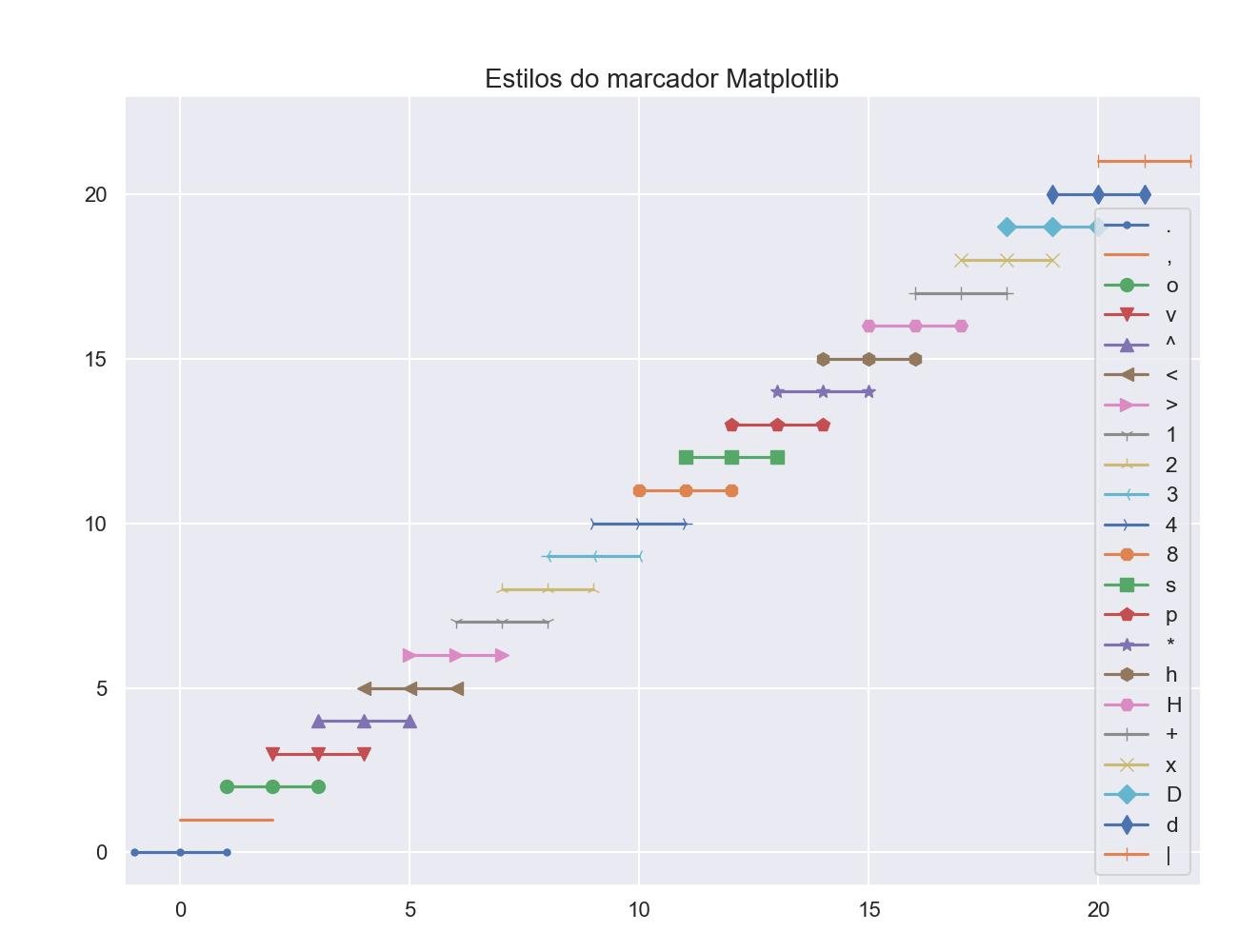

9.5.4 - Estilos de linha

import numpy as np
import matplotlib.pyplot as plt

estilos_linha = ['-.', '--', 'None', '-', ':']

plt.figure(figsize=(8, 5))
amostras = range(len(estilos_linha))

for i in amostras:
    plt.plot(
        [i-1, i, i+1], [i, i, i], 
        label='"%s"' %estilos_linha[i], 
        linestyle=estilos_linha[i],
        lw=4
    ) 

# Anotações 
    
plt.title('Estilos de linha Matplotlib', fontsize=20)
plt.ylim([-1, len(estilos_linha)+1])
plt.legend(loc='lower right')

plt.show()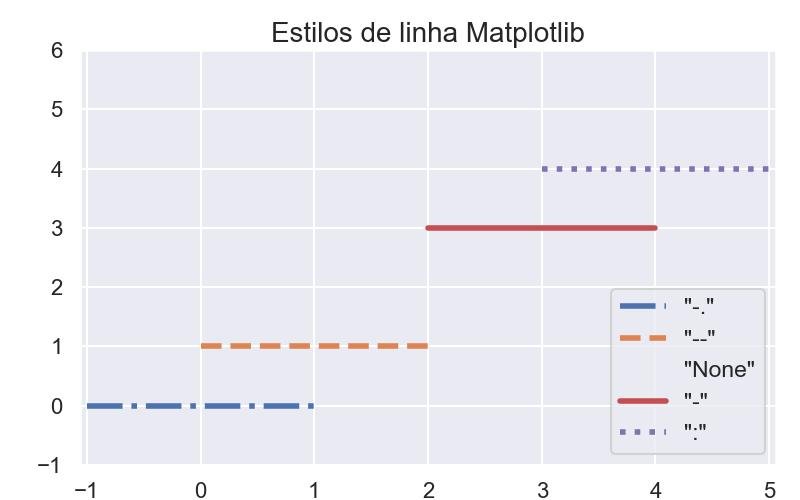

9.5.5 - Legendas extravagantes e transparentes

import numpy as np
import matplotlib.pyplot as plt

X1 = np.random.randn(100,2)
X2 = np.random.randn(100,2)
X3 = np.random.randn(100,2)

R1 = (X1**2).sum(axis=1)
R2 = (X2**2).sum(axis=1)
R3 = (X3**2).sum(axis=1)

plt.scatter(X1[:,0], X1[:,1],
            c='blue',
            marker='o',
            s=32. * R1,
            edgecolor='black',
            label='Dataset X1',
            alpha=0.7)
plt.scatter(X2[:,0], X2[:,1],
            c='gray',
            marker='s',
            s=32. * R2,
            edgecolor='black',
            label='Dataset X2',
            alpha=0.7)

plt.scatter(X2[:,0], X3[:,1],
            c='green',
            marker='^',
            s=32. * R3,
            edgecolor='black',
            label='Dataset X3',
            alpha=0.7)

plt.xlim([-3,3])
plt.ylim([-3,3])

leg = plt.legend(loc='upper left', fancybox=True)
leg.get_frame().set_alpha(0.5)

plt.show()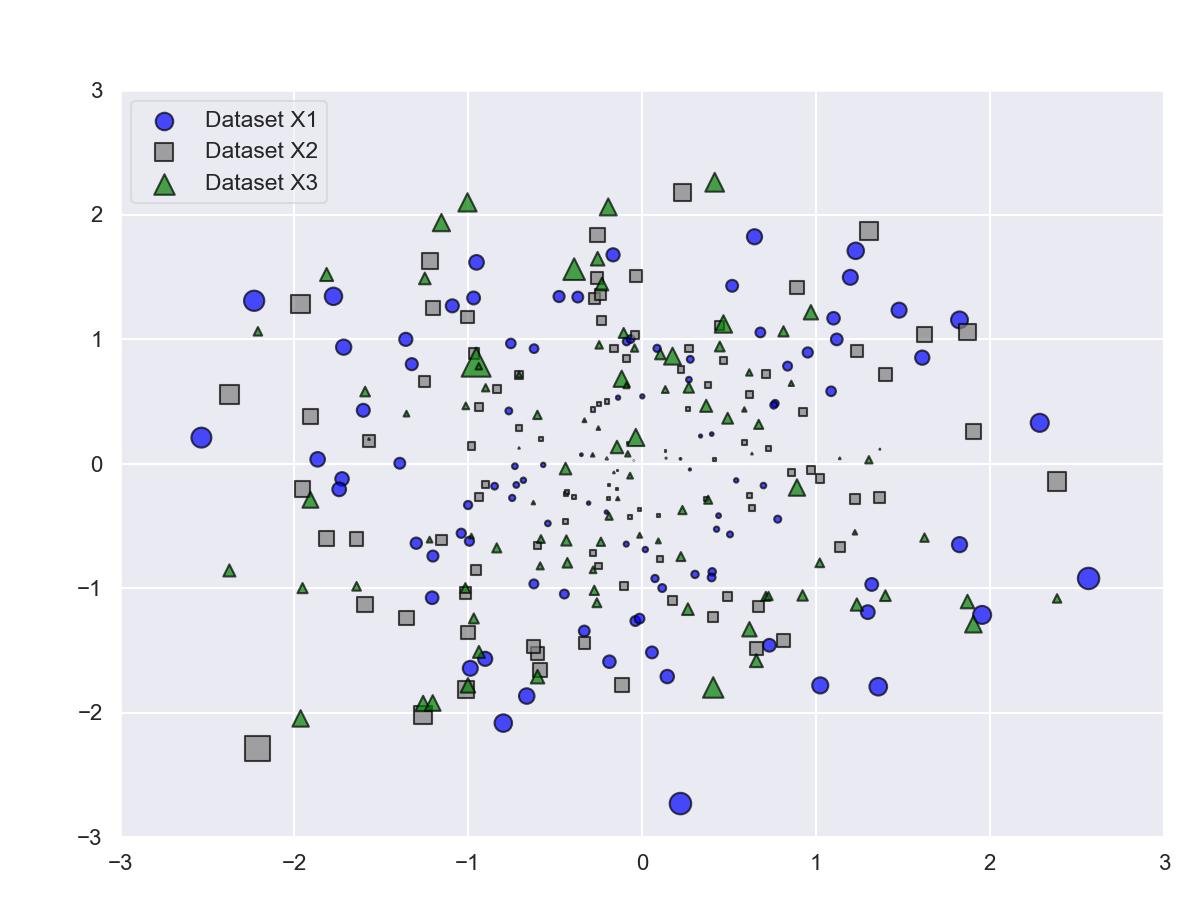

Escondendo eixos e etiquetas:

import numpy as np
import matplotlib.pyplot as plt

x = range(10)
y = range(10)

fig = plt.gca()

plt.plot(x, y)

fig.axes.get_xaxis().set_visible(False)
fig.axes.get_yaxis().set_visible(False)

plt.show()

Removendo quadro e traços:

import numpy as np
import matplotlib.pyplot as plt

x = range(10)
y = range(10)

fig = plt.gca()

plt.plot(x, y)

# removendo quadro
fig.spines["top"].set_visible(False)  
fig.spines["bottom"].set_visible(False)  
fig.spines["right"].set_visible(False)  
fig.spines["left"].set_visible(False) 

# removendo carrapatos
plt.tick_params(
    axis="both", which="both", bottom="off", top="off",  
    labelbottom="on", left="off", right="off", labelleft="on")  

plt.show()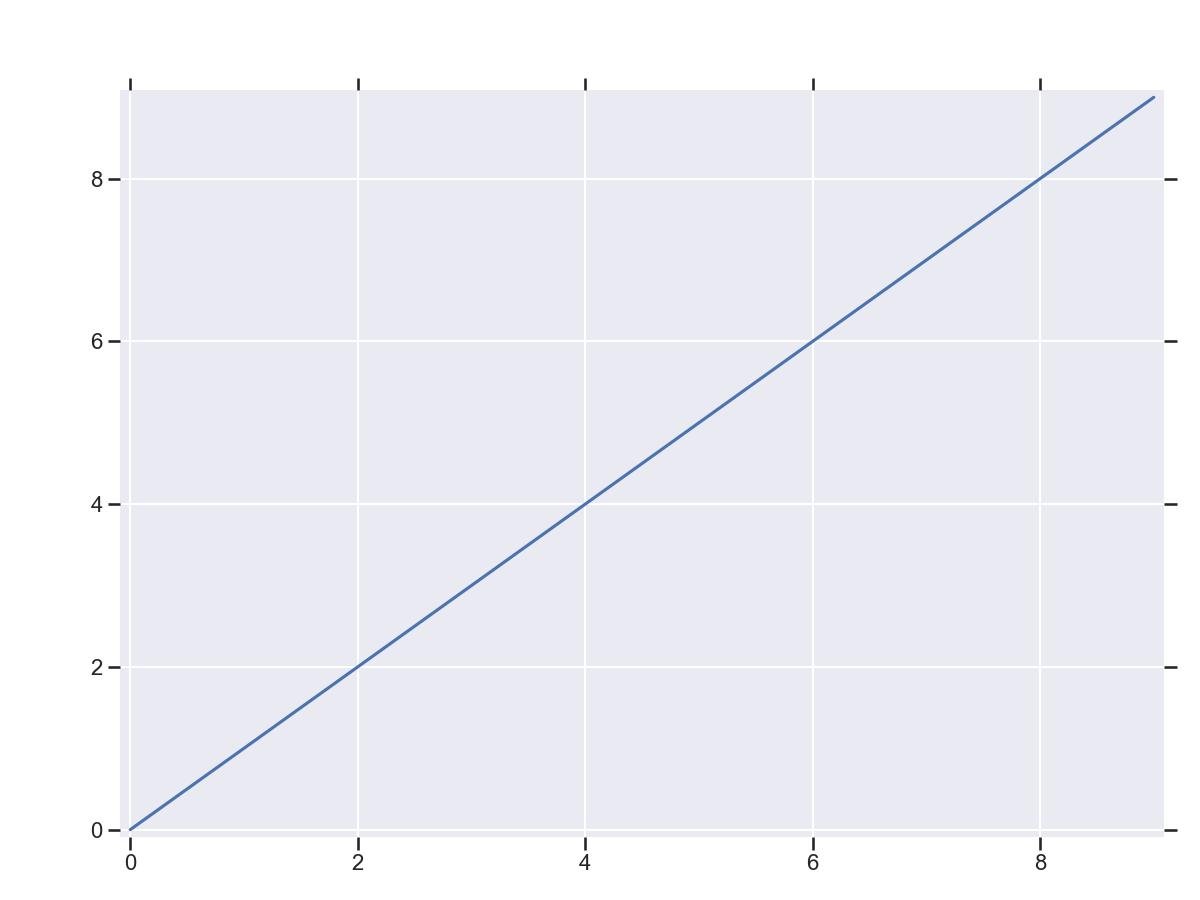

9.5.6 - Esquema do eixo estético

import numpy as np
import math
import matplotlib.pyplot as plt

X = np.random.normal(loc=0.0, scale=1.0, size=300)
width = 0.5
bins = np.arange(math.floor(X.min())-width, 
                 math.ceil(X.max())+width, 
                 width) # tamanho fixo da caixa

ax = plt.subplot(111)  

# remove axis at the top and to the right
ax.spines["top"].set_visible(False)  
ax.spines["right"].set_visible(False) 

# ocultar ticks do eixo
plt.tick_params(axis="both", which="both", bottom="off", top="off",  
                labelbottom="on", left="off", right="off", labelleft="on")

plt.hist(X, alpha=0.5, bins=bins)
plt.grid()

plt.xlabel('x etiqueta')
plt.ylabel('y etiqueta')
plt.title('título')

plt.show()

9.5.7 - Rótulos personalizados

Texto e rotação:

import matplotlib.pyplot as plt

x = range(10)
y = range(10)
labels = ['super long axis label' for i in range(10)]

fig, ax = plt.subplots()

plt.plot(x, y)

# definir rótulos de marca personalizados
ax.set_xticklabels(labels, rotation=45, horizontalalignment='right')

plt.show()

Adicionando um valor constante aos rótulos dos eixos:

import matplotlib.pyplot as plt

CONST = 10

x = range(10)
y = range(10)
labels = [i+CONST for i in x]

fig, ax = plt.subplots()

plt.plot(x, y)
plt.xlabel('x-value + 10')

# definir rótulos de marca personalizados
ax.set_xticklabels(labels)

plt.show()

9.5.8 - Aplicando personalização e configurações globalmente

Todo mundo tem uma percepção diferente de "estilo" e, normalmente, faríamos alguns pequenos ajustes nos visuais padrão do matplotlib aqui e ali. Após a personalização, seria tedioso repetir o mesmo código várias vezes toda vez que produzimos um novo gráfico. No entanto, temos várias opções para aplicar as alterações globalmente.

Configurações apenas para a sessão ativa:

Aqui, estamos interessados apenas nas configurações da sessão atual. Nesse caso, uma maneira de personalizar os padrões do matplotlibs seria o atributo 'rcParams' (na próxima sessão, você verá uma referência útil para todas as diferentes configurações do matplotlib). Por exemplo, se quisermos aumentar o tamanho da fonte de nossos títulos para todos os gráficos que seguem na sessão ativa, podemos digitar o seguinte:

import matplotlib as mpl
mpl.rcParams['axes.titlesize'] = '20'

Vejamos como fica:

from matplotlib import pyplot as plt
x = range(10)
y = range(10)

plt.plot(x, y)
plt.title('título maior')    
plt.show()

E se quisermos voltar às configurações padrão, podemos usar o comando:

mpl.rcdefaults()

Observe que temos que reexecutar a função mágica inline matplotlib depois:

plt.plot(x, y)
plt.title('tamanho do título padrão')    
plt.show()

9.5.9 - Linhas de grade

Gerando alguns dados de amostra:

import numpy as np
import random
from matplotlib import pyplot as plt

data = np.random.normal(0, 20, 1000) 

# tamanho fixo da caixa
bins = np.arange(-100, 100, 5) # tamanho fixo da caixa

plt.xlim([min(data)-5, max(data)+5])

plt.hist(data, bins=bins, alpha=0.5)
plt.show()

Grade padrão:

plt.hist(data, bins=bins, alpha=0.5)
plt.grid()

plt.show()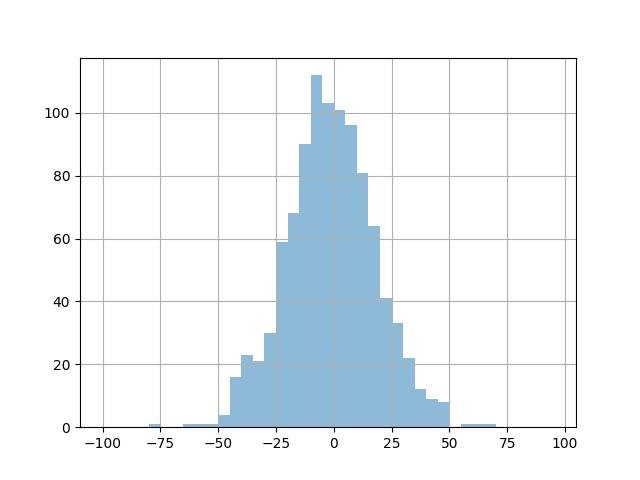

Ou alternativamente:

plt.hist(data, bins=bins, alpha=0.5)
ax = plt.gca()
ax.grid(True)

plt.show()

Grade vertical:

plt.hist(data, bins=bins, alpha=0.5)
ax = plt.gca()
ax.xaxis.grid(True)

plt.show()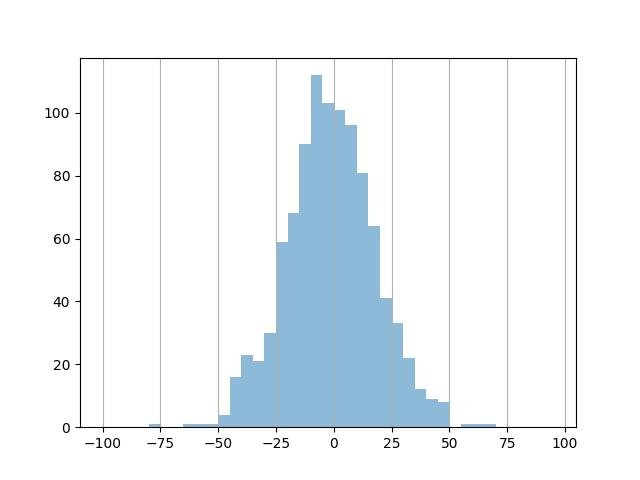

Grade horizontal:

plt.hist(data, bins=bins, alpha=0.5)
ax = plt.gca()
ax.yaxis.grid(True)

plt.show()

Agora controlamos estilo da linha de grade.

Mudando a frequência do tick:

import numpy as np

# Ticks principais a cada 10
major_ticks = np.arange(-100, 101, 10)                                              

ax = plt.gca()
ax.yaxis.grid()

ax.set_yticks(major_ticks)                                                       
                                    
plt.hist(data, bins=bins, alpha=0.5)

plt.show()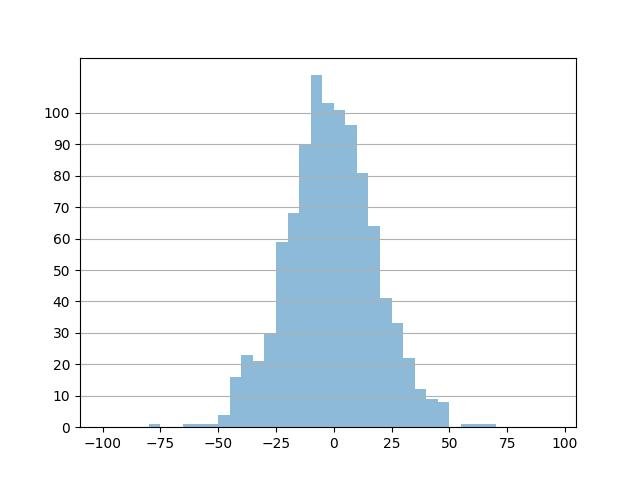

Alterando a cor do tick e o estilo de linha.

from matplotlib import rcParams

rcParams['grid.linestyle'] = '-'
rcParams['grid.color'] = 'blue'
rcParams['grid.linewidth'] = 0.2

plt.grid()
plt.hist(data, bins=bins, alpha=0.5)

plt.show()

9.5.10 - Legendas

De volta à estaca zero:

import matplotlib.pyplot as plt
import numpy as np

x = np.arange(10)

for i in range(1, 4):
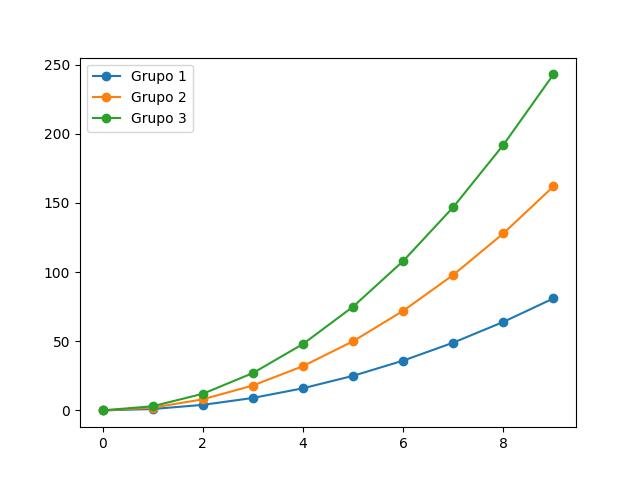
    plt.plot(x, i * x**2, label='Grupo %d' % i)

plt.legend(loc='best')
plt.show()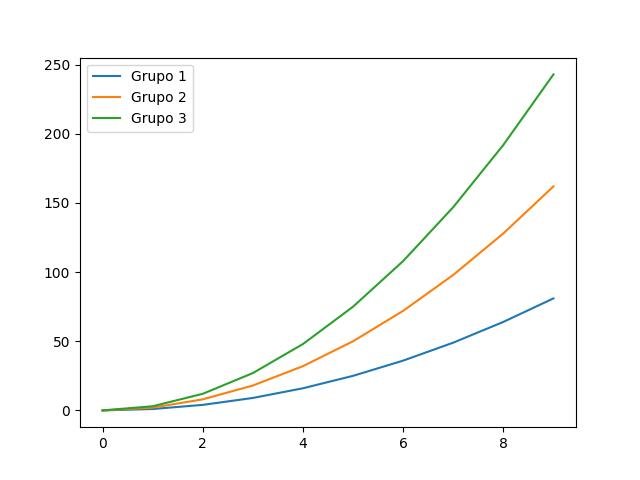

Vamos ficar chiques:

x = np.arange(10)

for i in range(1, 4):
    plt.plot(x, i * x**2, label='Grupo %d' % i)

plt.legend(loc='best', fancybox=True, shadow=True)
plt.show()

Pensando fora da caixa:

fig = plt.figure()
ax = plt.subplot(111)

x = np.arange(10)

for i in range(1, 4):
    ax.plot(x, i * x**2, label='Grupo %d' % i)

ax.legend(loc='upper center', 
          bbox_to_anchor=(0.5,  # horizontal
                          1.15),# vertical 
          ncol=3, fancybox=True)
plt.show()

fig = plt.figure()
ax = plt.subplot(111)

x = np.arange(10)

for i in range(1, 4):
    ax.plot(x, i * x**2, label='Grupo %d' % i)

ax.legend(
    loc='upper left', 
    bbox_to_anchor=(1., 1.),
    ncol=1, fancybox=True)
plt.show()

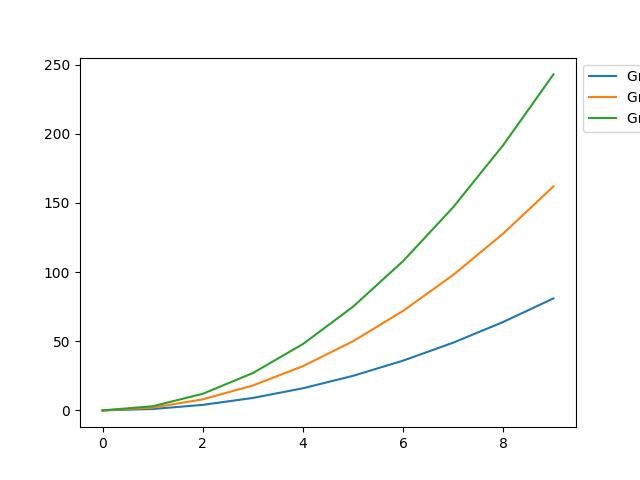
Amo quando as coisas são transparentes, livres e claras:

x = np.arange(10)

for i in range(1, 4):
    plt.plot(x, i * x**2, label='Grupo %d' % i)

plt.legend(loc='upper right', framealpha=0.1)
plt.show()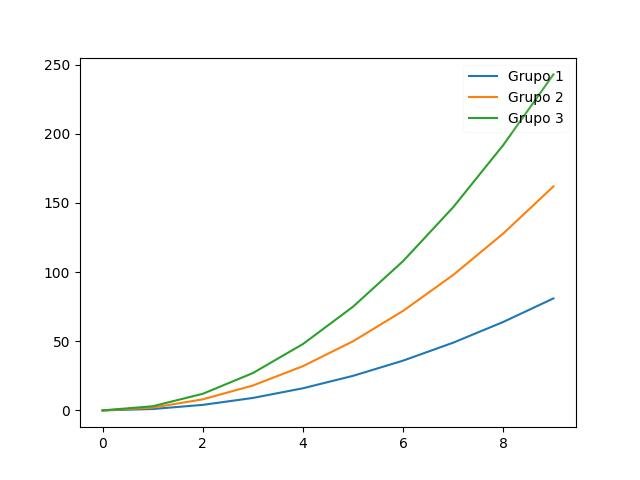

Marcadores: Todas as coisas boas vêm em trios!

from itertools import cycle
x = np.arange(10)

colors = ['blue', 'red', 'green']
color_gen = cycle(colors)

for i in range(1, 4):
    plt.scatter(x, i * x**2, label='Grupo %d' % i, color=next(color_gen))

plt.legend(loc='upper left')
plt.show()

from itertools import cycle
x = np.arange(10)

colors = ['blue', 'red', 'green']
color_gen = cycle(colors)

for i in range(1, 4):
    plt.scatter(x, i * x**2, label='Grupo %d' % i, color=next(color_gen))

plt.legend(loc='upper left', scatterpoints=1)
plt.show()

from itertools import cycle
x = np.arange(10)

colors = ['blue', 'red', 'green']
color_gen = cycle(colors)

for i in range(1, 4):
    plt.plot(x, i * x**2, label='Grupo %d' % i, marker='o')

plt.legend(loc='upper left')
plt.show()

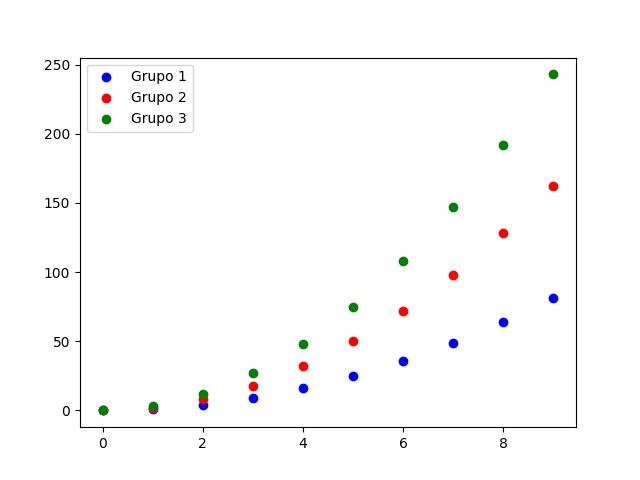
from itertools import cycle
x = np.arange(10)

colors = ['blue', 'red', 'green']
color_gen = cycle(colors)

for i in range(1, 4):
    plt.plot(x, i * x**2, label='Grupo %d' % i, marker='o')

plt.legend(loc='upper left', numpoints=1)
plt.show()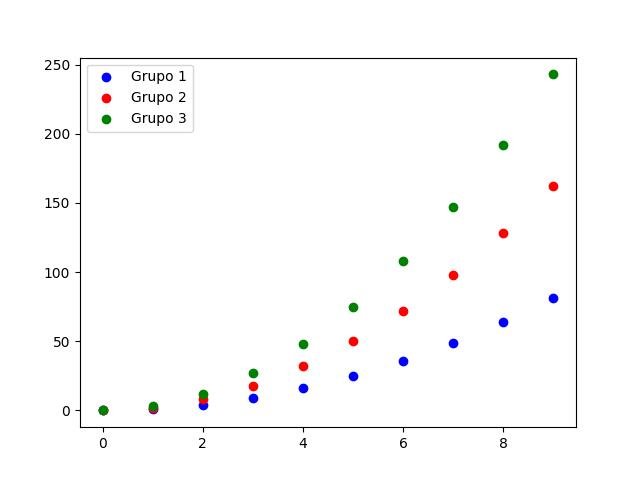

9.5.11 - Folhas de estilo

Um dos recursos mais legais adicionados ao matlotlib é o suporte para "estilos"!

A funcionalidade de "estilos" nos permite criar belos gráficos sem problemas, sendo um ótimo recurso!

Os estilos atualmente incluídos podem ser listados via print(plt.style.available):

import matplotlib.pyplot as plt
print(plt.style.available)

['Solarize_Light2', '_classic_test_patch', '_mpl-gallery', '_mpl-gallery-nogrid', 'bmh', 'classic', 'dark_background', 'fast', 'fivethirtyeight', 'ggplot', 'grayscale', 'seaborn', 'seaborn-bright', 'seaborn-colorblind', 'seaborn-dark', 'seaborn-dark-palette', 'seaborn-darkgrid', 'seaborn-deep', 'seaborn-muted', 'seaborn-notebook', 'seaborn-paper', 'seaborn-pastel', 'seaborn-poster', 'seaborn-talk', 'seaborn-ticks', 'seaborn-white', 'seaborn-whitegrid', 'tableau-colorblind10']

Existem duas maneiras de aplicar o estilo aos nossos gráficos.

Primeiro, podemos definir o estilo para nosso ambiente de codificação globalmente por meio da função plt.style.use():

import numpy as np

plt.style.use('ggplot')

x = np.arange(10)
for i in range(1, 4):
    plt.plot(x, i * x**2, label='Group %d' % i)

plt.legend(loc='best')
plt.show()

Outra maneira de usar estilos é por meio do gerenciador de contexto, que aplica o estilo apenas a um bloco de código específico:

with plt.style.context('fivethirtyeight'):
    for i in range(1, 4):
        plt.plot(x, i * x**2, label='Group %d' % i)
    plt.legend(loc='best')
    plt.show()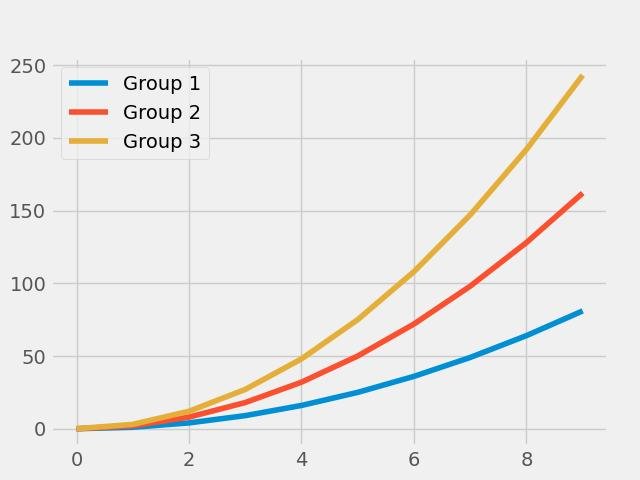

Finalmente, aqui está uma visão geral de como os diferentes estilos se parecem:

import math

n = len(plt.style.available)
num_rows = math.ceil(n/4)

fig = plt.figure(figsize=(15, 15))

for i, s in enumerate(plt.style.available):
    with plt.style.context(s):
        ax = fig.add_subplot(num_rows, 4, i+1)
        for i in range(1, 4):
            ax.plot(x, i * x**2, label='Group %d' % i)
            ax.set_xlabel(s, color='black')
            ax.legend(loc='best')
    
fig.tight_layout()
plt.show()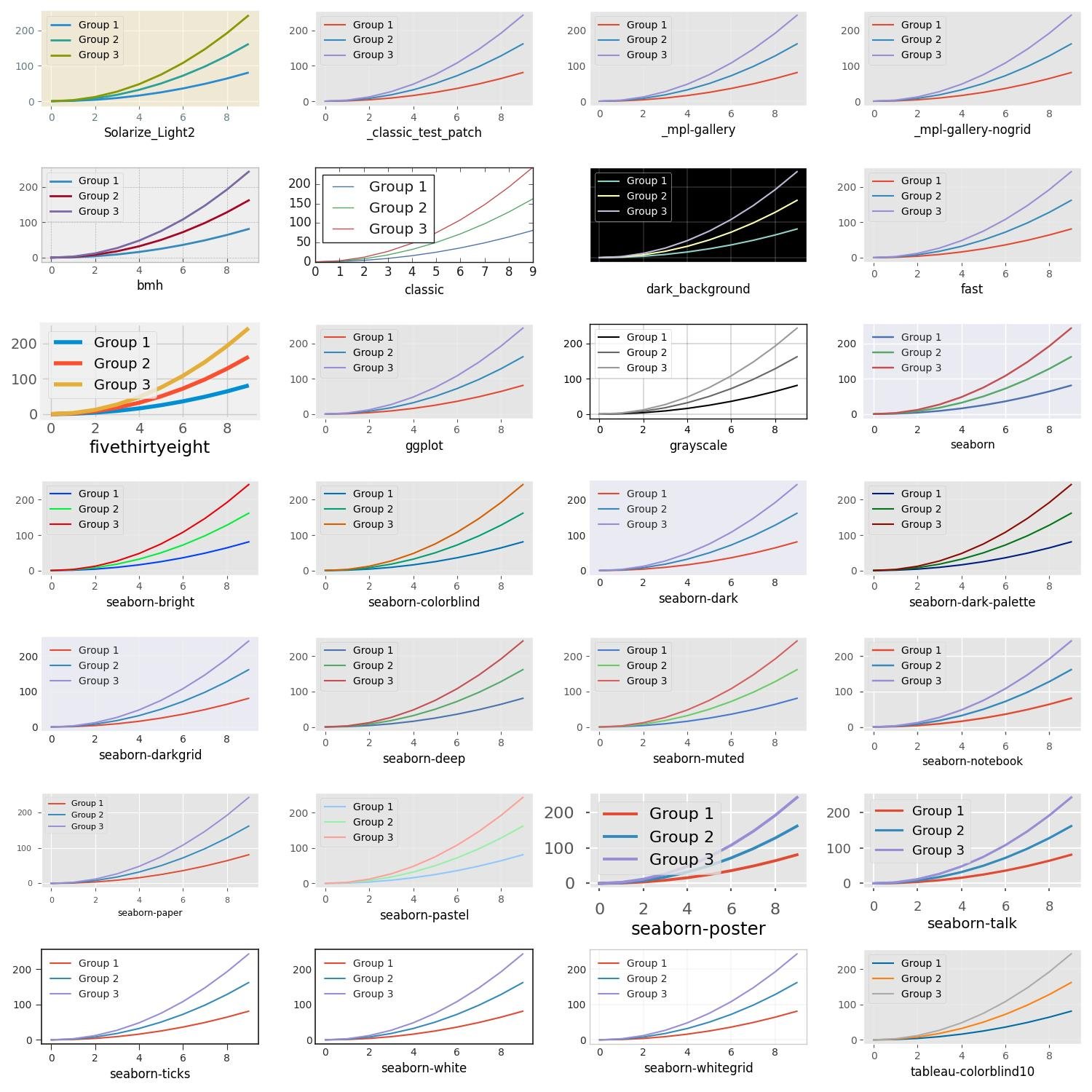

9.6 - Mapas de calor

Iniciamos importando os pacotes necessários:

import numpy as np
import matplotlib.pyplot as plt

Criamos as matrizes:

# Amostra de uma distribuição gaussiana bivariada
mean = [0,0]
cov = [[0,1],[1,0]] 
x, y = np.random.multivariate_normal(mean, cov, 10000).T

9.6.1 - Mapas de calor simples

Usando o histogram2d do NumPy:

hist, xedges, yedges = np.histogram2d(x,y)
X,Y = np.meshgrid(xedges,yedges)
plt.imshow(hist)
plt.grid(True)
plt.colorbar()
plt.show()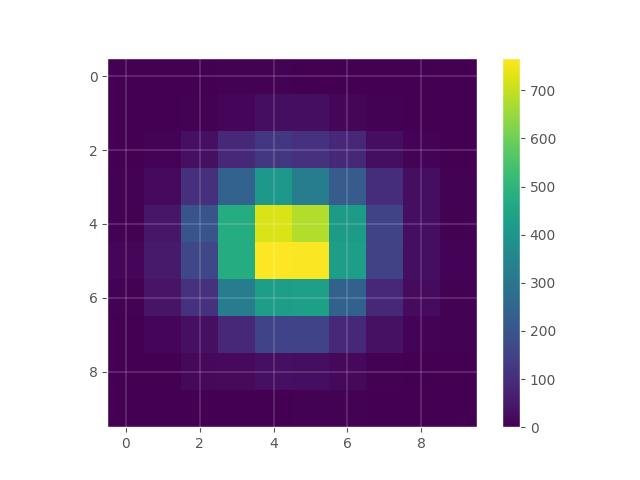

Mudando a interpolação:

plt.imshow(hist, interpolation='nearest')
plt.grid(True)
plt.colorbar()
plt.show()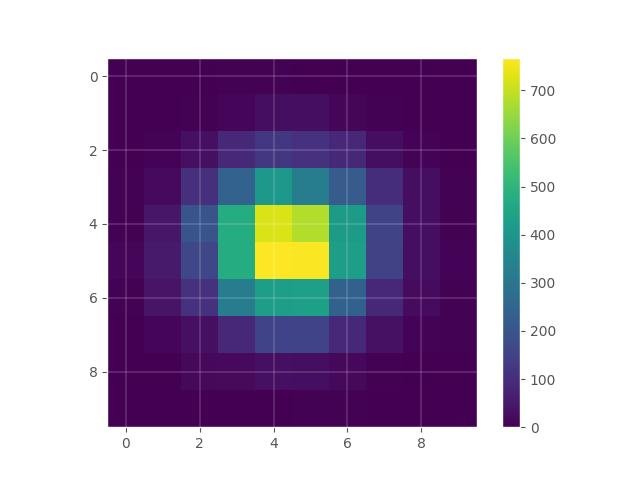

Usando hist2d de matplotlib:

plt.hist2d(x, y, bins=10)
plt.colorbar()
plt.grid()
plt.show()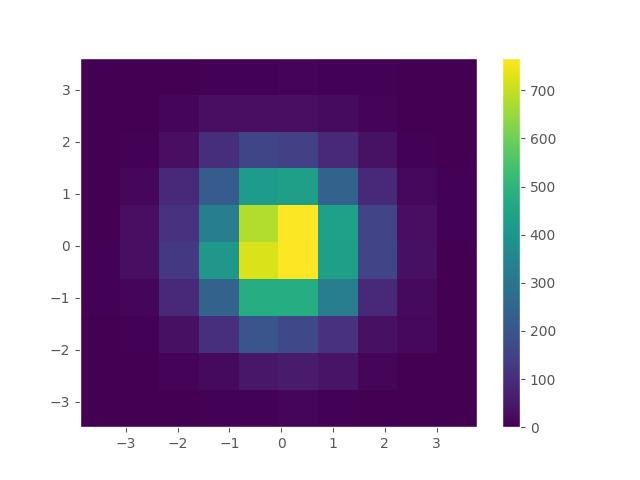

alterando o tamanho da caixa:

plt.hist2d(x, y, bins=40)
plt.colorbar()
plt.grid()
plt.show()

Usando pcolor do matplotlib:

plt.pcolor(hist)
plt.colorbar()
plt.grid()
plt.show()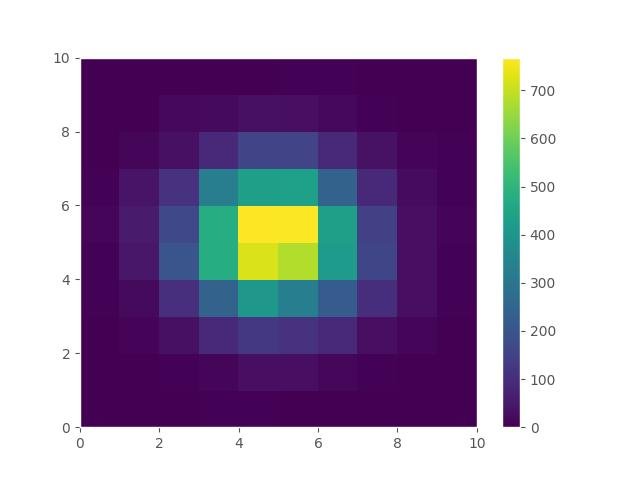

Usando a função matshow() de matplotlib:

import numpy as np
import matplotlib.pyplot as plt

columns = ['A', 'B', 'C', 'D']
rows = ['1', '2', '3', '4']

data = np.random.random((4,4))

fig = plt.figure()

ax = fig.add_subplot(111)

cax = ax.matshow(data, interpolation='nearest')
fig.colorbar(cax)

ax.set_xticklabels([''] + columns)
ax.set_yticklabels([''] + rows)

plt.show()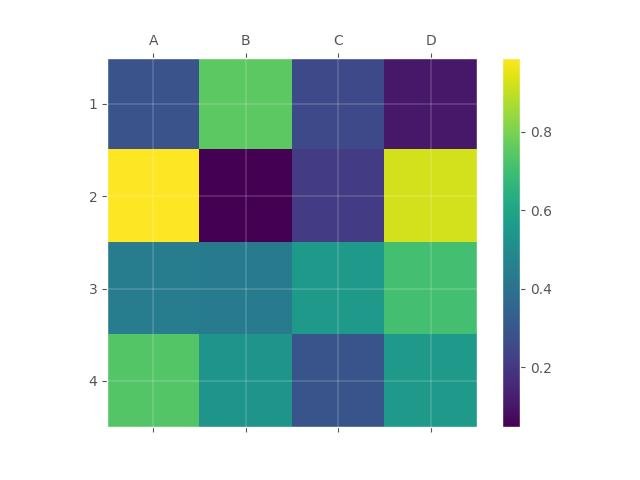

9.6.2 - Usando diferentes mapas de cores

Mapas de cores disponíveis:

from math import ceil
import numpy as np

# Sample from a bivariate Gaussian distribution
mean = [0,0]
cov = [[0,1],[1,0]] 
x, y = np.random.multivariate_normal(mean, cov, 10000).T

size = len(plt.cm.datad.keys())
all_maps = list(plt.cm.datad.keys())

fig, ax = plt.subplots(ceil(size/4), 4, figsize=(12,100))

counter = 0
for row in ax:
    for col in row:
        try:
            col.imshow(hist, cmap=all_maps[counter])
            col.set_title(all_maps[counter])
        except IndexError:
           break
        counter += 1

plt.tight_layout()
plt.show()

9.6.3 - Novos mapas de cores

Novos mapas de cores projetados por Stéfan van der Walt e Nathaniel Smith foram incluídos no matplotlib 1.5, e o mapa de cores viridis será o novo mapa de cores padrão no matplotlib 2.0.

from math import ceil
import numpy as np
from matplotlib import pyplot as plt

# Sample from a bivariate Gaussian distribution
mean = [0,0]
cov = [[0,1],[1,0]] 
x, y = np.random.multivariate_normal(mean, cov, 10000).T

size = len(plt.cm.datad.keys())
all_maps = list(plt.cm.datad.keys())

new_maps = ['viridis', 'inferno', 'magma', 'plasma']

counter = 0
for i in range(4):
    plt.subplot(1, 4, counter + 1)
    
    plt.imshow(hist, cmap=new_maps[counter])
    plt.title(new_maps[counter])
    counter += 1

plt.tight_layout()
plt.show()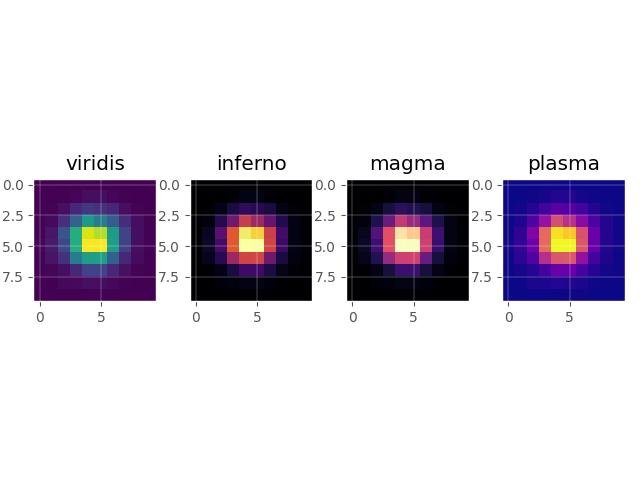

Criando mapas de calor com um mapa de cores em escala logarítmica:

import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm
import numpy as np

np.random.seed(1)
a = np.random.random((25, 25))

plt.subplot(1, 1, 1)
plt.pcolor(a, norm=LogNorm(vmin=a.min() / 1.2, vmax=a.max() * 1.2), cmap='PuBu_r')
plt.colorbar()

plt.show()

9.7 - Histogramas

9.7.1 - Histogramas simples

Tamanho do compartimento fixo:

import numpy as np
import random
from matplotlib import pyplot as plt

data = np.random.normal(0, 20, 1000) 

# tamanho fixo da caixa
bins = np.arange(-100, 100, 5) # tamanho fixo da caixa

plt.xlim([min(data)-5, max(data)+5])

plt.hist(data, bins=bins, alpha=0.5)
plt.title('Dados gaussianos aleatórios (tamanho fixo da caixa)')
plt.xlabel('variável X (bin size = 5)')
plt.ylabel('contagem')

plt.show()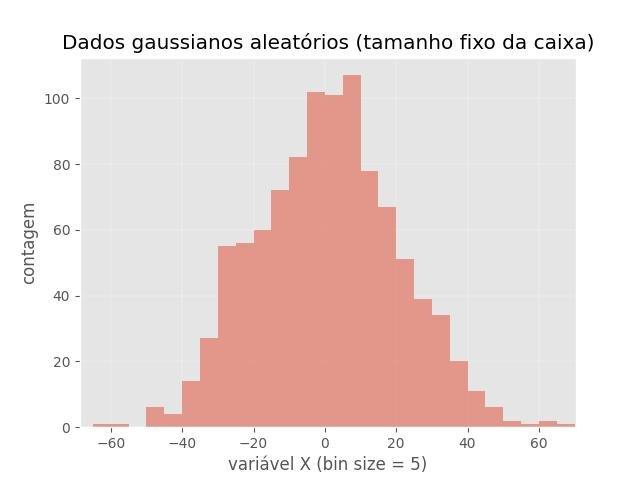

Número fixo de caixas:

import numpy as np
import random
import math
from matplotlib import pyplot as plt

data = np.random.normal(0, 20, 1000) 

bins = np.linspace(math.ceil(min(data)), 
                   math.floor(max(data)),
                   20) # fixed number of bins

plt.xlim([min(data)-5, max(data)+5])

plt.hist(data, bins=bins, alpha=0.5)
plt.title('Dados gaussianos aleatórios (número fixo de compartimentos)')
plt.xlabel('variável X (20 evenly spaced bins)')
plt.ylabel('contagem')

plt.show()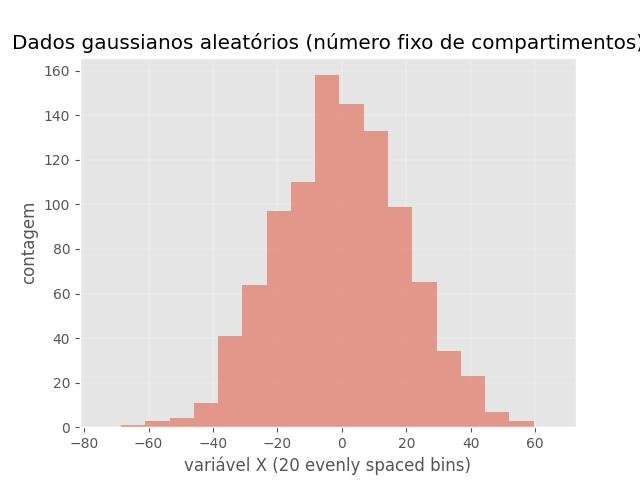

9.7.2 - Histograma de 2 conjuntos de dados sobrepostos

import numpy as np
import random
from matplotlib import pyplot as plt

data1 = [random.gauss(15,10) for i in range(500)]  
data2 = [random.gauss(5,5) for i in range(500)]  
bins = np.arange(-60, 60, 2.5)
plt.xlim([min(data1+data2)-5, max(data1+data2)+5])

plt.hist(data1, bins=bins, alpha=0.3, label='class 1')
plt.hist(data2, bins=bins, alpha=0.3, label='class 2')
plt.title('Dados gaussianos aleatórios')
plt.xlabel('variável X')
plt.ylabel('contagem')
plt.legend(loc='upper right')

plt.show()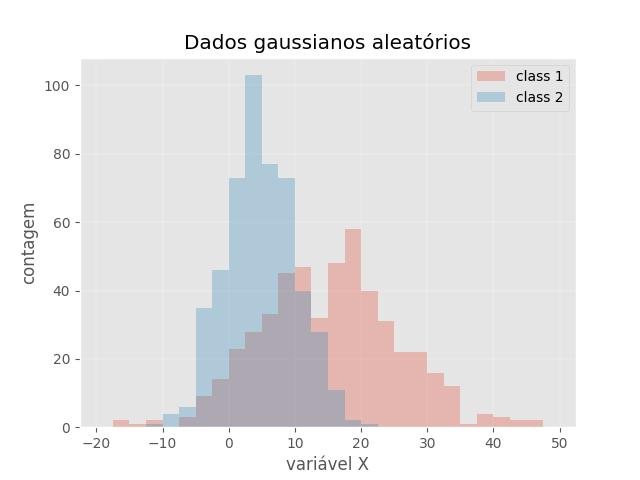

import numpy as np
import random
import math
from matplotlib import pyplot as plt
from scipy.interpolate import interp1d
from scipy.stats import norm

data = np.random.normal(0, 20, 10000) 

# traçando o histograma
n, bins, patches = plt.hist(data, bins=20, alpha=0.5, color='lightblue')

# ajustando os dados
mu, sigma = norm.fit(data)

# adicionando a linha ajustada
y = norm.pdf(bins, mu, sigma)
interp = interp1d(bins, y, kind='cubic')
plt.plot(bins, interp(y), linewidth=2, color='blue')

plt.xlim([min(data)-5, max(data)+5])
plt.title('Dados gaussianos aleatórios (número fixo de compartimentos)')
plt.xlabel('variável X (20 evenly spaced bins)')
plt.ylabel('contagem')

plt.show()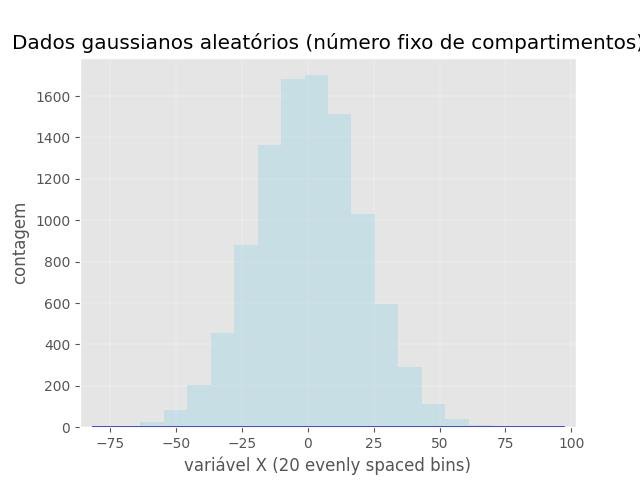

9.7.3 - Histograma mostrando as alturas das barras, mas sem a área sob as barras

O gráfico de linha abaixo está usando compartimentos de um histograma e é particularmente útil se você estiver trabalhando com muitos conjuntos de dados sobrepostos diferentes.

# Gera um conjunto de dados gaussiano aleatório com diferentes meios
# 5 linhas com 30 colunas, onde cada linha representa 1 amostra.
import numpy as np

data = np.ones((5,30))
for i in range(5):
    data[i,:] = np.random.normal(loc=i/2, scale=1.0, size=30)

Por meio da função np.histogram(), podemos categorizar nossos dados em compartimentos distintos.

from math import floor, ceil # para arredondar para cima e para baixo

data_min = floor(data.min()) # minimum val. of the dataset rounded down
data_max = floor(data.max()) # maximum val. of the dataset rounded up

bin_size = 0.5
bins = np.arange(floor(data_min), ceil(data_max), bin_size)
print(np.histogram(data[0,:], bins=bins))

(array([1, 6, 4, 7, 6, 3, 1, 1, 1, 0, 0], dtype=int64), array([-2. , -1.5, -1. , -0.5,  0. ,  0.5,  1. ,  1.5,  2. ,  2.5,  3. ,
        3.5]))

A função numpy.histogram retorna uma tupla, onde o primeiro valor é uma matriz de quantas amostras caem no primeiro compartimento, no segundo compartimento e assim por diante.

O segundo valor é outro array NumPy; ele contém os compartimentos especificados. Observe que todos os bins, exceto o último, são intervalos semi-abertos, por exemplo, o primeiro bin seria [-2, -1,5) (incluindo -2, mas não incluindo -1,5) e o segundo bin seria [-1,5, - 1.) (incluindo -1,5, mas não incluindo 1,0). Mas o último bin é definido como [2., 2.5] (incluindo 2 e incluindo 2.5).

from matplotlib import pyplot as plt
marcadores = ['^', 'v', 'o', 'p', 'x', 's', 'p', ',']
plt.figure(figsize=(13,8))
for row in range(data.shape[0]):
    hist = np.histogram(data[row,:], bins=bins)
    plt.errorbar(hist[1][:-1] + bin_size/2, 
        hist[0],  
        alpha=0.3,
        xerr=bin_size/2,
        capsize=0,
        fmt=marcadores[row],
        linewidth=8,
    )
plt.legend(['sample %s'%i for i in range(1, 6)])
plt.grid()
plt.title('Histograma mostrando as alturas das barras, mas sem a área sob as barras', fontsize=18)
plt.ylabel('contagem', fontsize=14)
plt.xlabel('Valor de X value (tamanho do compartimento = %s)'%bin_size, fontsize=14)
plt.xticks(bins + bin_size)
plt.show()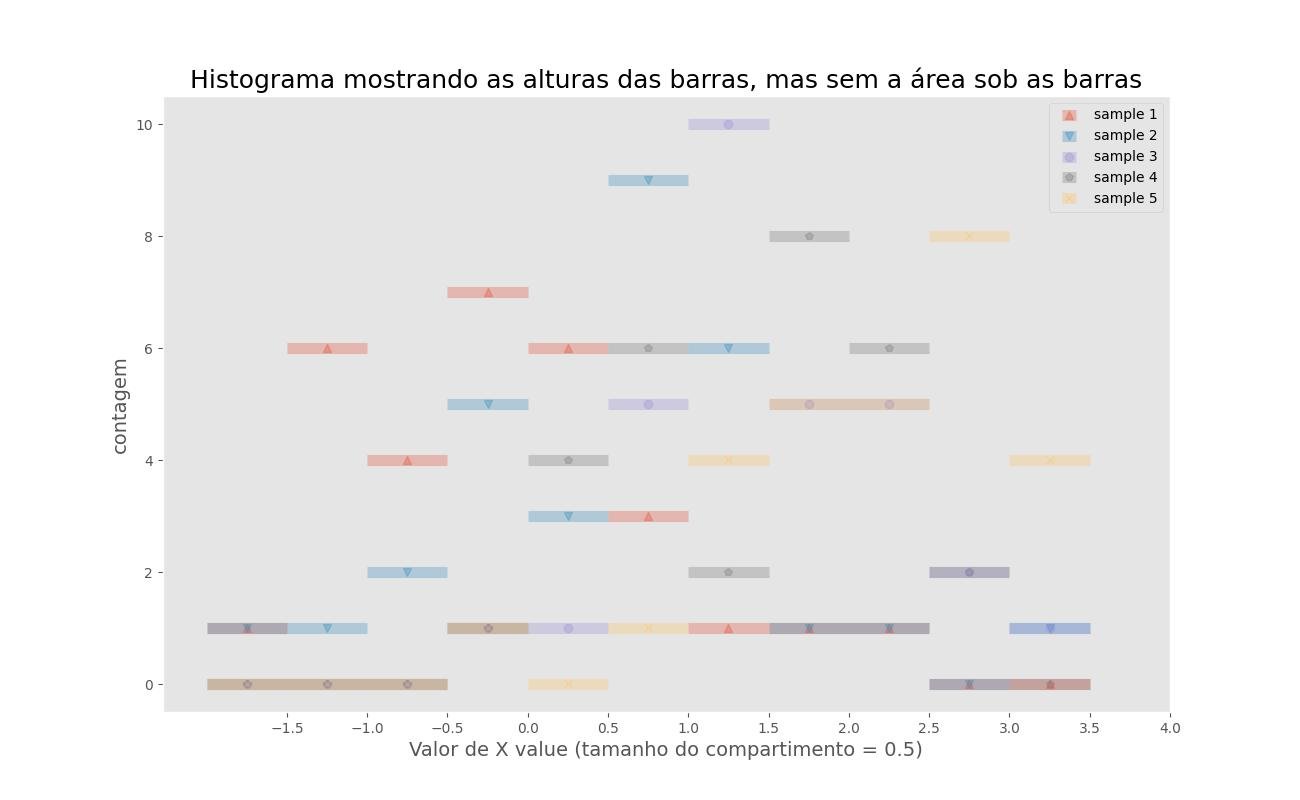

9.8 - Gráficos de linhas

9.8.1 - Plotagem de linhas simples

import matplotlib.pyplot as plt

x = [1, 2, 3]

y_1 = [50, 60, 70]
y_2 = [20, 30, 40]

plt.plot(x, y_1, marker='x')
plt.plot(x, y_2, marker='^')

plt.xlim([0, len(x)+1])
plt.ylim([0, max(y_1+y_2) + 10])
plt.xlabel('x-axis etiqueta')
plt.ylabel('y-axis etiqueta')
plt.title('Gráfico de linha simples')
plt.legend(['amostra 1', 'amostra 2'], loc='upper left')

plt.show()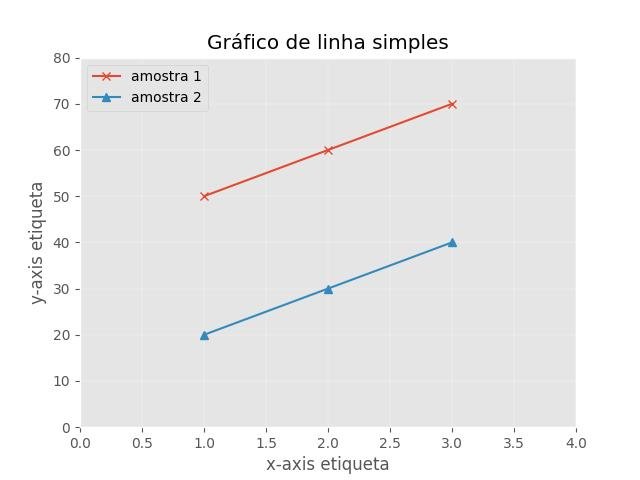

9.8.2 - Gráfico de linha com barras de erro

import matplotlib.pyplot as plt

x = [1, 2, 3]

y_1 = [50, 60, 70]
y_2 = [20, 30, 40]

y_1_err = [4.3, 4.5, 2.0] 
y_2_err = [2.3, 6.9, 2.1] 

x_labels = ["x1", "x2", "x3"]

plt.errorbar(x, y_1, yerr=y_1_err, fmt='-x')
plt.errorbar(x, y_2, yerr=y_2_err, fmt='-^')

plt.xticks(x, x_labels)
plt.xlim([0, len(x)+1])
plt.ylim([0, max(y_1+y_2) + 10])
plt.xlabel('x-axis etiqueta')
plt.ylabel('y-axis etiqueta')
plt.title('Gráfico de linha com barras de erro')
plt.legend(['amostra 1', 'amostra 2'], loc='upper left')

plt.show()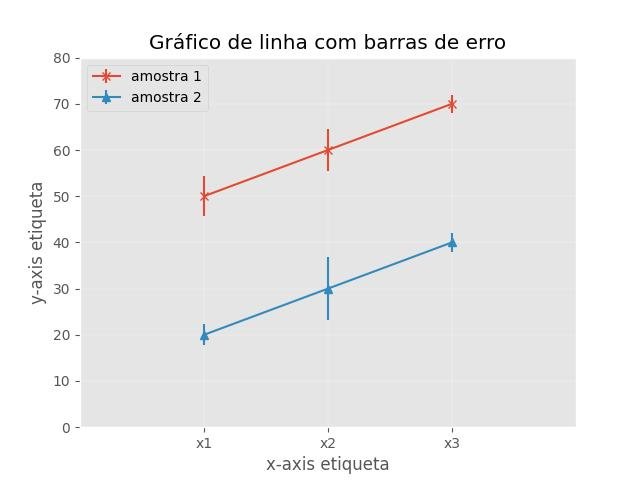

9.8.2.0.1 - plot with x-axis labels and log-scale

import matplotlib.pyplot as plt
x = [1, 2, 3]
y_1 = [0.5,7.0,60.0]
y_2 = [0.3,6.0,30.0]
x_labels = ["x1", "x2", "x3"]
plt.plot(x, y_1, marker='x')
plt.plot(x, y_2, marker='^')
plt.xticks(x, x_labels)
plt.xlim([0,4])
plt.xlabel('x-axis etiqueta')
plt.ylabel('y-axis etiqueta')
plt.yscale('log')
plt.title('Gráfico de linhas com rótulos do eixo x e escala logarítmica')
plt.legend(['amostra 1', 'amostra 2'], loc='upper left')
plt.show()

9.8.3 - Gaussian probability density functions

import numpy as np
from matplotlib import pyplot as plt
import math
def pdf(x, mu=0, sigma=1):
    """
    Calculates the normal distribution's probability density 
    function (PDF).      
    """
    term1 = 1.0 / ( math.sqrt(2*np.pi) * sigma )
    term2 = np.exp( -0.5 * ( (x-mu)/sigma )**2 )
    return term1 * term2
x = np.arange(0, 100, 0.05)
pdf1 = pdf(x, mu=5, sigma=2.5**0.5)
pdf2 = pdf(x, mu=10, sigma=6**0.5)
plt.plot(x, pdf1)
plt.plot(x, pdf2)
plt.title('Funções de densidade de probabilidade')
plt.ylabel('p(x)')
plt.xlabel('variável aleatória x')
plt.legend(['pdf1 ~ N(5,2.5)', 'pdf2 ~ N(10,6)'], loc='upper right')
plt.ylim([0,0.5])
plt.xlim([0,20])
plt.show()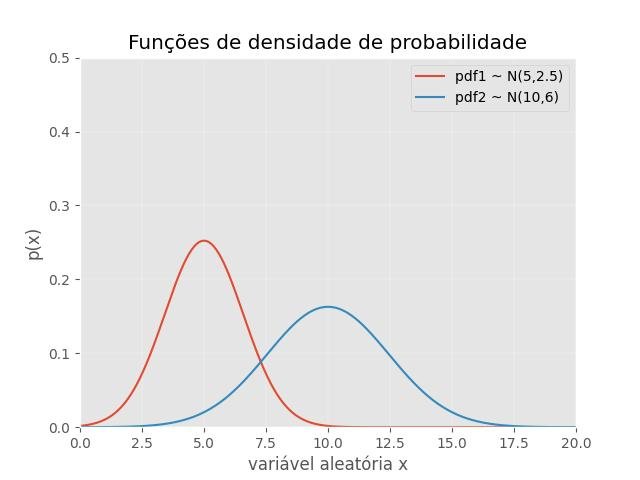

9.8.4 - Parcelas cumulativas

Soma cumulativa:

import numpy as np
import matplotlib.pyplot as plt

# soma cumulativa com np.cumsum()
A = np.arange(1, 11)
B = np.random.randn(10) # 10 rand. values from a std. norm. distr.
C = B.cumsum()

# São subplotados dois gráficosgráfico mostrando as funções cumulativas 
fig, (ax0, ax1) = plt.subplots(ncols=2, sharex=True, sharey=True, figsize=(10,5))

## A) via plt.step()

ax0.step(A, C, label='soma cumulativa')
ax0.scatter(A, B, label='Valores atuais')
ax0.set_ylabel('Y value')
ax0.legend(loc='upper right')

## B) via plt.plot()

ax1.plot(A, C, label='soma cumulativa')
ax1.scatter(A, B, label='Valores atuais')
ax1.legend(loc='upper right')

fig.text(0.5, 0.04, 'Número da amostra', ha='center', va='center')
fig.text(0.5, 0.95, 'Soma cumulativa de 10 amostras de uma distribuição normal aleatória', ha='center', va='center')

plt.show()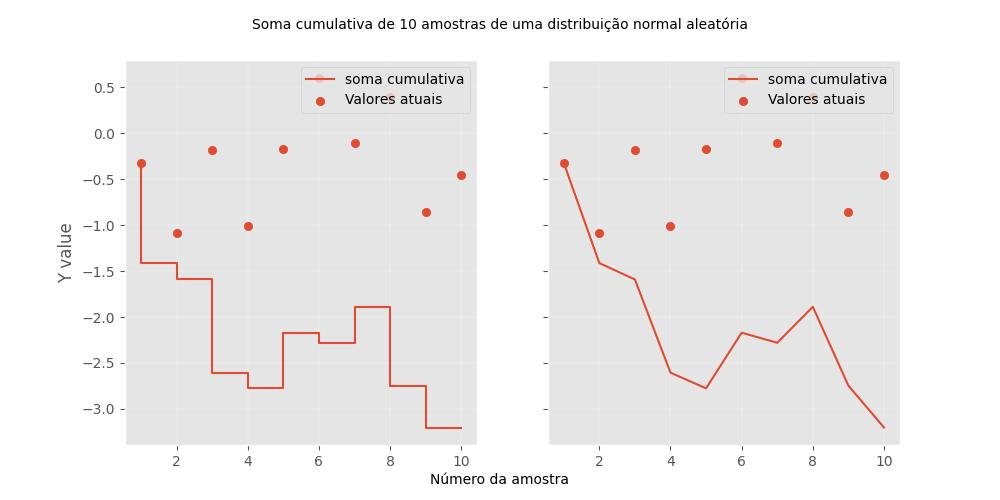

Contagem absoluta:

import numpy as np
import matplotlib.pyplot as plt

A = np.arange(1, 11)
B = np.random.randn(10) # 10 rand. values from a std. norm. distr.

plt.figure(figsize=(10,5))

plt.step(np.sort(B), A) 
plt.ylabel('contagem de amostras')
plt.xlabel('valor x')
plt.title('Número de amostras em um determinado limite')

plt.show()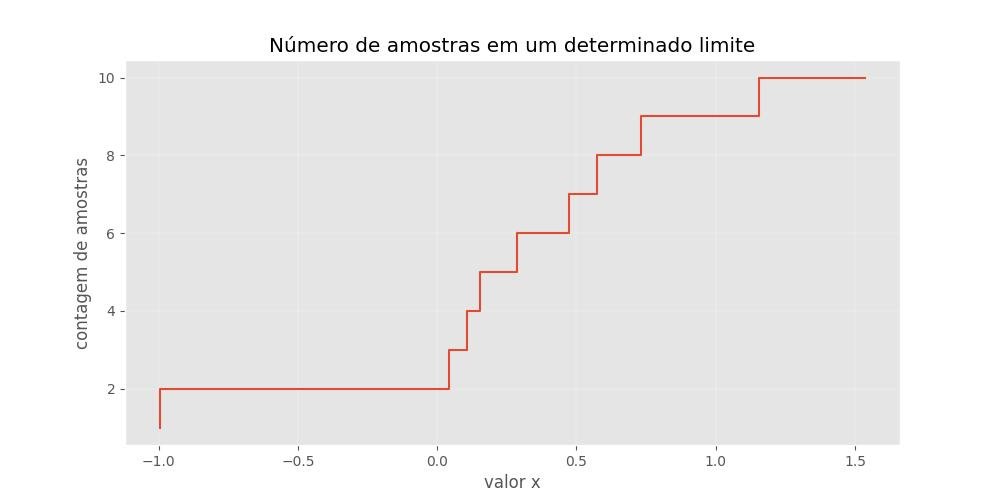

9.8.5 - Mapas de cores

Mais mapas de cores estão disponíveis em Scipy - Mapas de cores.

import numpy as np
import matplotlib.pyplot as plt

fig, (ax0, ax1) = plt.subplots(1,2, figsize=(14, 7))
amostras = range(1,16)

# Default Color Cycle

for i in amostras:
    ax0.plot([0, 10], [0, i], label=i, lw=3) 

# Mapa de cores Paired

colormap = plt.cm.Paired
plt.gca().set_prop_cycle(color=[colormap(i) for i in np.linspace(0, 0.9, len(amostras))])

for i in amostras:
    ax1.plot([0, 10], [0, i], label=i, lw=3) 

# Anotações 

ax0.set_title('Ciclo de cores padrão')
ax1.set_title('Mapa de cores plt.cm.Paired')
ax0.legend(loc='upper left')
ax1.legend(loc='upper left')

plt.show()

9.8.6 - Estilos de marcadores

import numpy as np
import matplotlib.pyplot as plt

marcadores = [
    '.', # point
    ',', # pixel
    'o', # circle
    'v', # triangle down
    '^', # triangle up
    '<', # triangle_left
    '>', # triangle_right
    '1', # tri_down
    '2', # tri_up
    '3', # tri_left
    '4', # tri_right
    '8', # octagon
    's', # square
    'p', # pentagon
    '*', # star
    'h', # hexagon1
    'H', # hexagon2
    '+', # plus
    'x', # x
    'D', # diamond
    'd', # thin_diamond
    '|', # vline
]

plt.figure(figsize=(13, 10))
amostras = range(len(marcadores))

for i in amostras:
    plt.plot([i-1, i, i+1], [i, i, i], label=marcadores[i], marker=marcadores[i], markersize=10) 

# Anotações 
    
plt.title('Estilos de marcadores Matplotlib', fontsize=20)
plt.ylim([-1, len(marcadores)+1])
plt.legend(loc='lower right')

plt.show()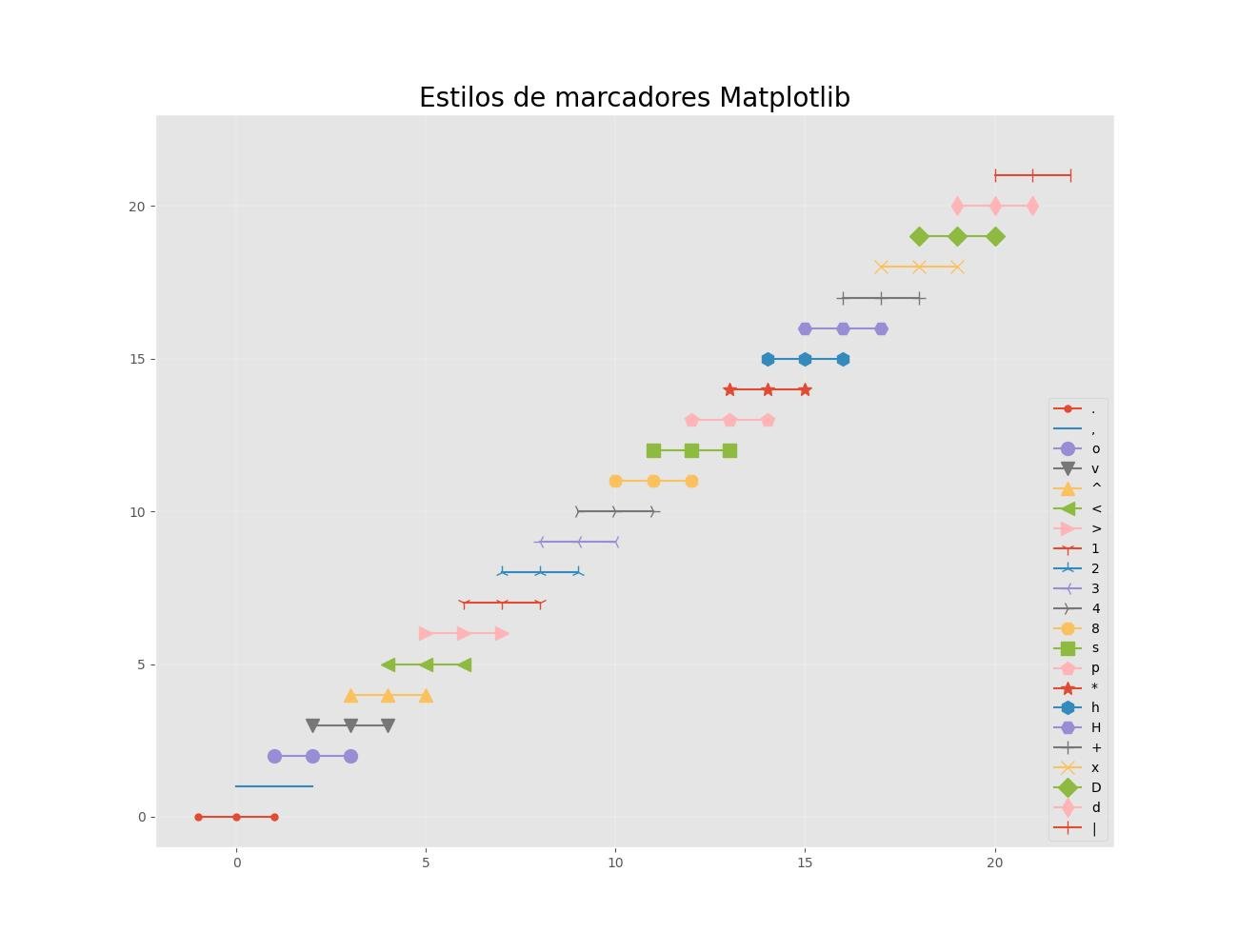

9.8.7 - Estilos de linha

import numpy as np
import matplotlib.pyplot as plt

estilos_linha = ['-.', '--', 'None', '-', ':']

plt.figure(figsize=(8, 5))
amostras = range(len(estilos_linha))

for i in amostras:
    plt.plot(
        [i-1, i, i+1], [i, i, i], 
        label='"%s"' %estilos_linha[i], 
        linestyle=estilos_linha[i],
        lw=4
    ) 

# Anotações 
    
plt.title('Estilos de linha Matplotlib', fontsize=20)
plt.ylim([-1, len(estilos_linha)+1])
plt.legend(loc='lower right')

plt.show()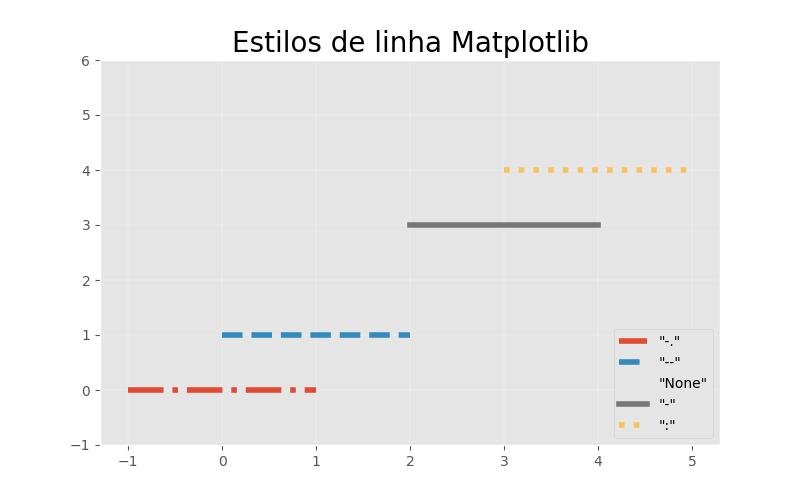

9.9 - Gráficos de dispersão

9.9.1 - Gráfico de dispersão básico

from matplotlib import pyplot as plt
import numpy as np

# Gerando um conjunto de dados Gaussion: criando vetores aleatórios,
# a partir da distribuição normal multivariada dada média e covariância.
mu_vec1 = np.array([0,0])
cov_mat1 = np.array([[2,0],[0,2]])

x1_amostras = np.random.multivariate_normal(mu_vec1, cov_mat1, 100)
x2_amostras = np.random.multivariate_normal(mu_vec1+0.2, cov_mat1+0.2, 100)
x3_amostras = np.random.multivariate_normal(mu_vec1+0.4, cov_mat1+0.4, 100)

# x1_amostras.shape -> (100, 2), 100 rows, 2 columns

plt.figure(figsize=(8,6))
    
plt.scatter(x1_amostras[:,0], x1_amostras[:,1], marker='x', 
            color='blue', alpha=0.7, label='x1 amostras')
plt.scatter(x2_amostras[:,0], x1_amostras[:,1], marker='o', 
            color='green', alpha=0.7, label='x2 amostras')
plt.scatter(x3_amostras[:,0], x1_amostras[:,1], marker='^', 
            color='red', alpha=0.7, label='x3 amostras')
plt.title('Gráfico de dispersão básico')
plt.ylabel('Variável X')
plt.xlabel('Variável Y')
plt.legend(loc='upper right')

plt.show()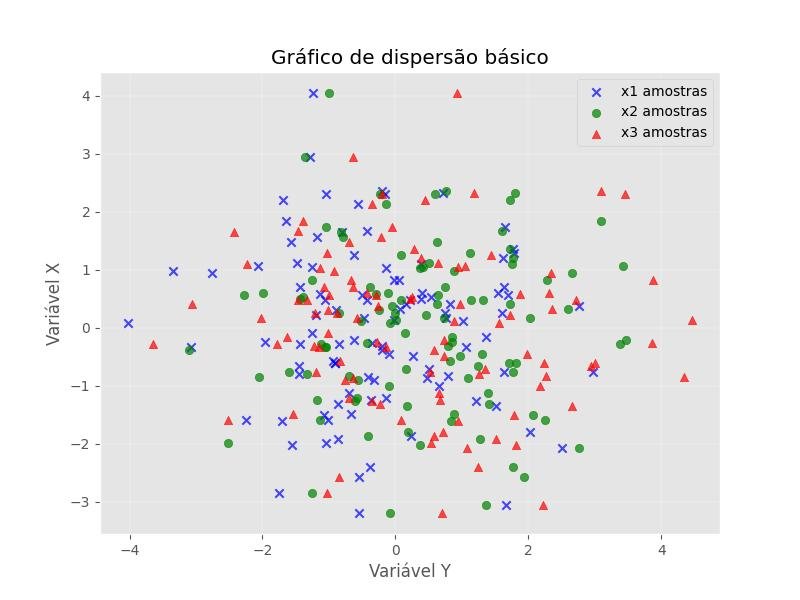

9.9.2 - Gráfico de dispersão com rótulos

import matplotlib.pyplot as plt

x_coords = [0.13, 0.22, 0.39, 0.59, 0.68, 0.74, 0.93]
y_coords = [0.75, 0.34, 0.44, 0.52, 0.80, 0.25, 0.55]

fig = plt.figure(figsize=(8,5))
plt.scatter(x_coords, y_coords, marker='s', s=50)

for x, y in zip(x_coords, y_coords):
    plt.annotate(
        '(%s, %s)' %(x, y), 
        xy=(x, y), 
        xytext=(0, -10),
        textcoords='offset points', 
        ha='center', 
        va='top')

plt.xlim([0,1])
plt.ylim([0,1])
plt.show()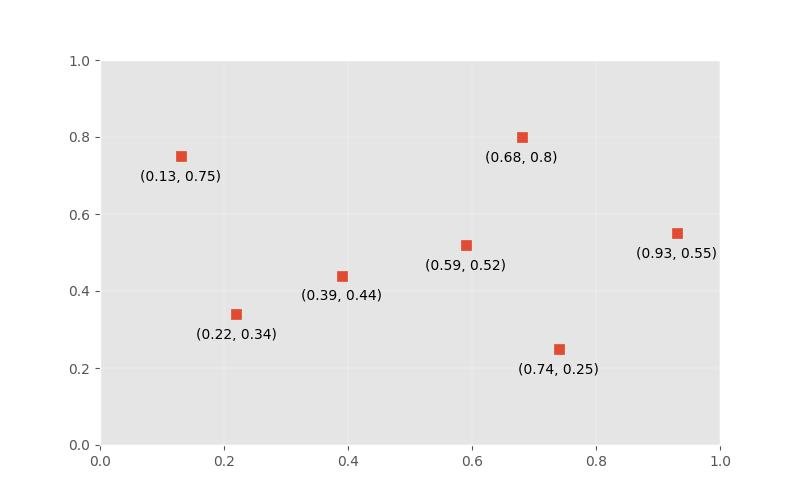

9.9.3 - Gráfico de dispersão de 2 classes com limite de decisão

# Classificação de 2 categorias com dados aleatórios de amostra 2D
# de uma distribuição normal multivariada
import numpy as np
from matplotlib import pyplot as plt

def decision_boundary(x_1):
    """ Calculates the x_2 value for plotting the decision boundary."""
    return 4 - np.sqrt(-x_1**2 + 4*x_1 + 6 + np.log(16))

# Gerando um conjunto de dados Gaussion: criando vetores aleatórios a partir
# da distribuição normal multivariada dada média e covariância
mu_vec1 = np.array([0,0])
cov_mat1 = np.array([[2,0],[0,2]])
x1_amostras = np.random.multivariate_normal(mu_vec1, cov_mat1, 100)
mu_vec1 = mu_vec1.reshape(1,2).T # to 1-col vector

mu_vec2 = np.array([1,2])
cov_mat2 = np.array([[1,0],[0,1]])
x2_amostras = np.random.multivariate_normal(mu_vec2, cov_mat2, 100)
mu_vec2 = mu_vec2.reshape(1,2).T # to 1-col vector

# Gráfico de dispersão principal e anotação do gráfico
f, ax = plt.subplots(figsize=(7, 7))
ax.scatter(x1_amostras[:,0], x1_amostras[:,1], marker='o', color='green', s=40, alpha=0.5)
ax.scatter(x2_amostras[:,0], x2_amostras[:,1], marker='^', color='blue', s=40, alpha=0.5)
plt.legend(['Class1 (w1)', 'Class2 (w2)'], loc='upper right') 
plt.title('Densidades de 2 classes com 25 padrões aleatórios bivariados cada')
plt.ylabel('x2')
plt.xlabel('x1')
ftext = 'p(x|w1) ~ N(mu1=(0,0)^t, cov1=I)\np(x|w2) ~ N(mu2=(1,1)^t, cov2=I)'
plt.figtext(.15,.8, ftext, fontsize=11, ha='left')

# Adicionando limite de decisão ao gráfico
x_1 = np.arange(-5, 5, 0.1)
bound = decision_boundary(x_1)
plt.plot(x_1, bound, 'r--', lw=3)

x_vec = np.linspace(*ax.get_xlim())
x_1 = np.arange(0, 100, 0.05)

plt.show()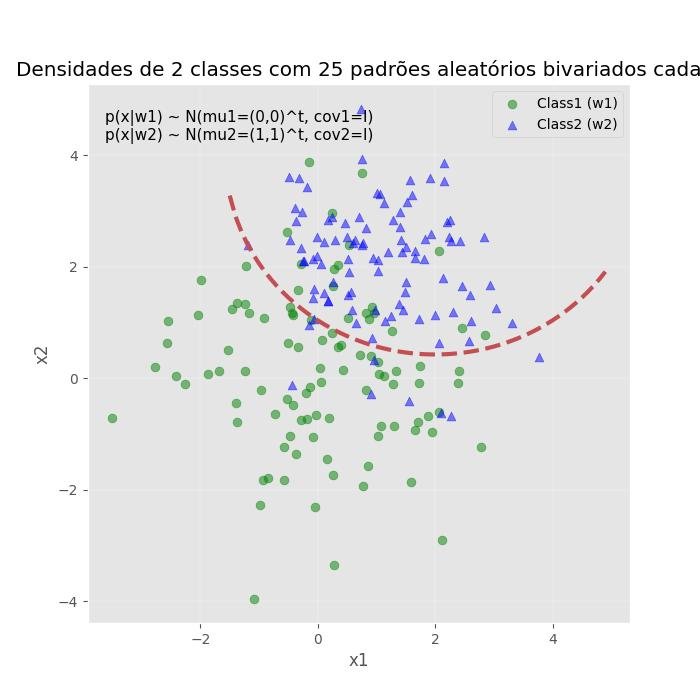

9.9.4 - Aumentando o tamanho do ponto com a distância da origem

import numpy as np
import matplotlib.pyplot as plt

fig = plt.figure(figsize=(8,6))

# Gerando um conjunto de dados Gaussion:
# criando vetores aleatórios a partir da distribuição normal multivariada
# dada média e covariância
mu_vec1 = np.array([0,0])
cov_mat1 = np.array([[1,0],[0,1]])
X = np.random.multivariate_normal(mu_vec1, cov_mat1, 500)
R = X**2
R_sum = R.sum(axis=1)
plt.scatter(X[:, 0], X[:, 1], 
            color='gray', 
            marker='o', 
            s=32. * R_sum,
            edgecolor='black',
            alpha=0.5)
plt.show()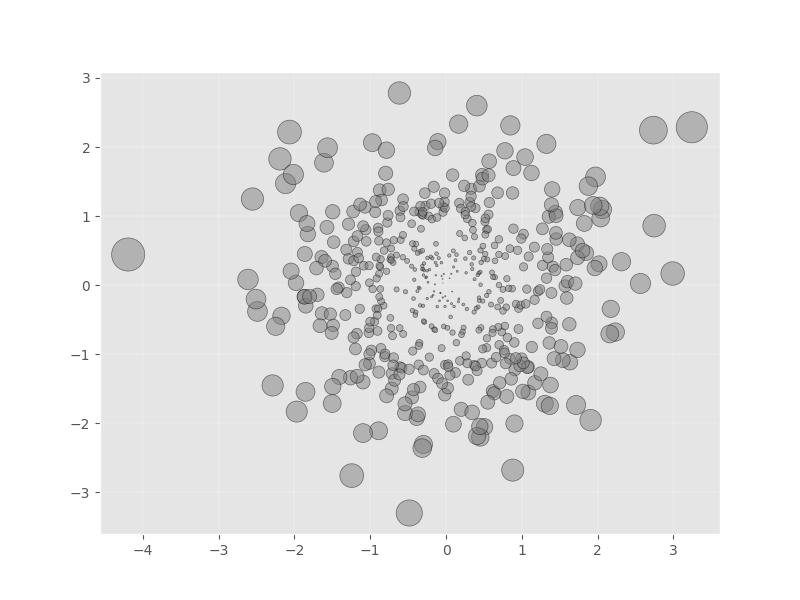

9.10 - Gráficos especiais

9.10.1 - gráfico de pizza básico

from matplotlib import pyplot as plt
import numpy as np

plt.pie(
    (10,5),
    labels=('spam','ham'),
    shadow=True,
    colors=('yellowgreen', 'lightskyblue'),
    explode=(0,0.15), # space between slices 
    startangle=90,    # rotate conter-clockwise by 90 degrees
    autopct='%1.1f%%',# display fraction as percentage
    )
plt.legend(fancybox=True)
plt.axis('equal')     # plot pyplot as circle
plt.tight_layout()
plt.show()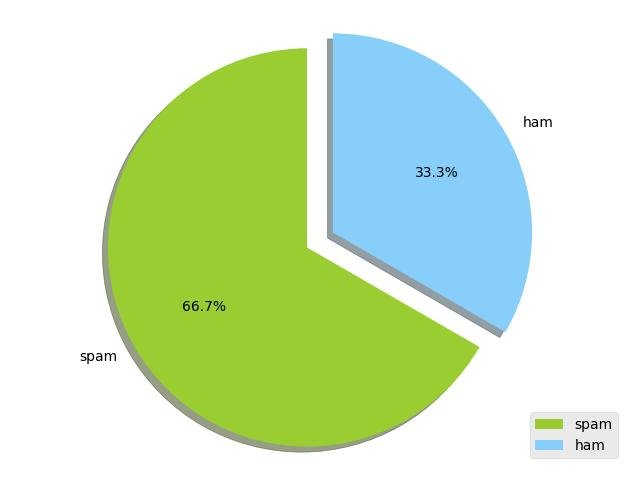

9.10.2 - Triangulação básica

from matplotlib import pyplot as plt
import matplotlib.tri as tri
import numpy as np

rand_data = np.random.randn(50, 2)

triangulacao = tri.Triangulation(rand_data[:,0], rand_data[:,1])

plt.triplot(triangulacao)

plt.show()

9.10.3 - Plotagens estilo xkcd

import matplotlib.pyplot as plt

x = [1, 2, 3]

y_1 = [50, 60, 70]
y_2 = [20, 30, 40]

with plt.xkcd():

    plt.plot(x, y_1, marker='x')
    plt.plot(x, y_2, marker='^')

    plt.xlim([0, len(x)+1])
    plt.ylim([0, max(y_1+y_2) + 10])

    plt.xlabel('x-axis label')
    plt.ylabel('y-axis label')

    plt.title('Gráfico de linha simples')

    plt.legend(['amostra 1', 'amostra 2'], loc='upper left')

    plt.show()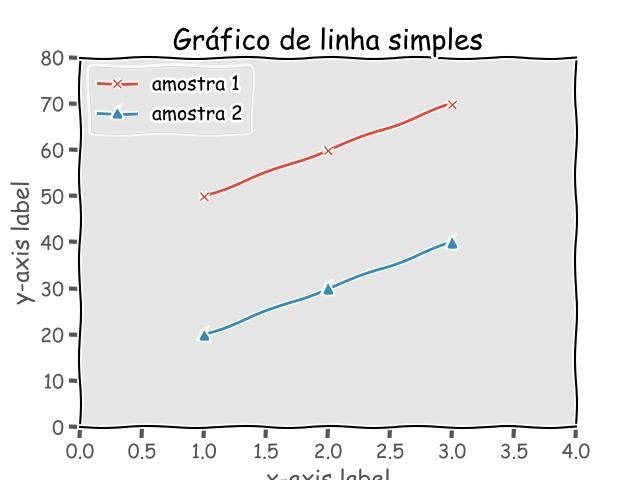

import numpy as np
import random
from matplotlib import pyplot as plt

data = np.random.normal(0, 20, 1000) 
bins = np.arange(-100, 100, 5) # tamanho fixo da caixa

with plt.xkcd():
    plt.xlim([min(data)-5, max(data)+5])
    plt.hist(data, bins=bins, alpha=0.5)
    plt.title('Dados gaussianos aleatórios (tamanho fixo da caixa)')
    plt.xlabel('variável X (tamanho da caixa = 5)')
    plt.ylabel('contagem')
    plt.show()

from matplotlib import pyplot as plt
import numpy as np

with plt.xkcd():
    X = np.random.random_integers(1,5,5) # 5 random integers within 1-5
    cols = ['b', 'g', 'r', 'y', 'm']
    plt.pie(X, colors=cols)
    plt.legend(X)
    plt.show()

Arduino

Coautor

Betobyte

Autor

Autores

||| Áreas ||| Estatística ||| Python ||| Projetos ||| Dicas & Truques ||| Quantum ||| Matplotlib || Python para Iniciantes || Python Básico || Matplotlib || Numpy || Seaborn || Pandas || Django || Estatística para Cientistas de Dados || Python com ML Básico || Python com ML Básico || Aulas | Introdução (introdução, pyplot, plotagem, pacotes complementares) | Gráficos básicos (barra, pizza, linhas, pontos) | Customizações (cores, linhas, marcadores) | Gráficos elaborados (pista, radial, bolhas) | Distribuições (violino, densidade, histograma, caixa, cumeeira) | Correlações (dispersão, calor, correlograma, bolha, dispersão conectada, densidade 2d) | Partições (árvore, venn, rosca, pizza, dentrograma, empacotamento circular) | Classificações (barras, radar, nuvem de palavras, paralelas, pirulito, barras circulares) | Galeria (Gráfico de dispersão 3D, GD 3D com autovetores, Cubo 3D, Distribuição Gaussiana Multivariada com superfície colorida, DGM como grade de malha, Gráfico de Barras Vertical com barras de erro, GB horizontal com barras de erro, GB back-to-back, GB agrupadas, GB empilhadas, GB com rótulos, GB com rotação, GB com gradiente de cores, preenchimento de padrão, Gráficos de Caixa (boxplot), GC preta e branca, GC, horizontal, GC cheia, GC personalizadas, GC e barra de violinos, GC simples, subplots, cores, eixo estético, rótulos personalizados, linhas de grade, folhas de estilos, mapas de calor, de cores, histogramas, e mais.) |