1 - Introdução à Estatística Avançada

Nesta seção, iremos revisitar as medidas de tendência central, como a média, a mediana e a moda.

Essas medidas desempenham um papel fundamental na descrição e resumo dos dados, fornecendo insights sobre o centro ou a tendência central de um conjunto de observações.

Ao explorar essas medidas de tendência central, forneceremos exemplos práticos que ilustram sua aplicação em diferentes contextos, incluindo campos como ciências sociais, economia, saúde, engenharia e muito mais.

Você verá como essas medidas podem ser utilizadas para resumir e comparar dados, ajudando a identificar padrões, tendências e características importantes em uma ampla gama de situações.

Através dessa revisão, você será capaz de entender como as medidas de tendência central podem ser calculadas e interpretadas corretamente, proporcionando uma base sólida para a compreensão dos tópicos avançados de estatística.

1.2.1.1 - Média

A média é a medida mais comumente usada para representar a tendência central dos dados.

Ela é calculada somando todos os valores de um conjunto de observações e dividindo a soma pelo número total de observações.

Exploraremos exemplos práticos para mostrar como calcular a média em diferentes contextos, como média aritmética, média ponderada e média geométrica.

• Média Aritmética: tipo mais comum de média utilizado na estatística, calculada somando todos os valores em um conjunto de dados e dividindo o resultado pelo número de observações. A média aritmética é uma medida de tendência central e representa o valor médio dos dados. É amplamente utilizada para resumir conjuntos de dados numéricos e é representada pelo símbolo "x̄" ou "μ" (para uma população).
• Média Ponderada: semelhante à média aritmética, mas atribui pesos diferentes aos valores do conjunto de dados. Os pesos representam a importância relativa de cada valor na média final. Para calcular a média ponderada, multiplica-se cada valor pelos respectivos pesos, soma-se os produtos e divide-se pelo somatório dos pesos. A média ponderada é útil quando certos valores têm mais impacto ou representatividade do que outros no conjunto de dados.
• Média Geométrica: usada principalmente para calcular a taxa de crescimento média de uma série de números ao longo do tempo. É calculada como a raiz n-ésima do produto dos valores, onde "n" é o número total de observações. A média geométrica é útil quando se trabalha com dados que apresentam um crescimento exponencial ou multiplicativo. Por exemplo, é frequentemente usada para calcular o retorno médio de investimentos financeiros ao longo do tempo.

Cada tipo de média tem sua própria aplicação e interpretação. A média aritmética é amplamente utilizada para resumir conjuntos de dados e determinar o valor médio geral. A média ponderada leva em consideração pesos diferentes, atribuindo maior importância a certos valores. A média geométrica é usada para calcular taxas de crescimento médias. A escolha do tipo de média depende do objetivo da análise estatística e das características dos dados em questão.

Veremos também como a média pode ser influenciada por valores extremos e como interpretá-la corretamente em relação à distribuição dos dados.

1.2.1.1.1 - Média aritmética

A média aritmética, também conhecida como média simples, é uma medida de tendência central amplamente utilizada na estatística. É calculada somando todos os valores em um conjunto de dados e dividindo o resultado pelo número de observações.

Fórmula da média aritmética: $ma$ = $\frac{x_1 + x_2 + x_3 + ... + x_n}{n}$, onde $ma$ é média aritmética, $x_1$, $x_2$, $x_3$, ..., $x_n$ são os valores do conjunto de dados e $n$ é o número total de observações.

Por exemplo, vamos considerar o conjunto de dados [10, 15, 20, 25, 30]. Para calcular a média aritmética, somamos todos os valores e dividimos pelo número de observações:

$ma$ = $\frac{10 + 15 + 20 + 25 + 30}{5}$ = $\frac{100}{5}$ = $20$

Portanto, a média aritmética dos valores fornecidos é igual a 20.

A média aritmética é amplamente utilizada como uma medida de tendência central, pois representa o valor médio dos dados, sendo sensível a todos os valores no conjunto de dados, o que significa que qualquer alteração nos valores afetará o valor da média. Além disso, a média aritmética pode ser calculada para diferentes tipos de dados, incluindo números inteiros, números reais, e até mesmo para certos tipos de dados categóricos.

É importante ressaltar que a média aritmética pode não ser uma representação adequada dos dados em certos casos, especialmente quando há valores extremos (outliers) que podem distorcer o resultado. Nesses casos, outras medidas de tendência central, como a mediana ou a média truncada, podem ser consideradas.

No entanto, a média aritmética é uma medida simples e amplamente compreendida, tornando-a útil para resumir e comparar conjuntos de dados. Ela fornece uma estimativa geral do valor médio de um conjunto de observações e é amplamente utilizada em estudos estatísticos, pesquisas, análises de dados e muitas outras aplicações.

Exemplo: cálculo da média de uma lista de valores usando a biblioteca Numpy.

import numpy as np

# Exemplo de lista de valores
valores = [15, 5, 10, 25, 20]

# Calcular a média usando a função mean() do Numpy
media = np.mean(valores)

# Imprimir o resultado
print("A média dos valores é:", media)

A média dos valores é: 15.0

Utilizando a função np.mean() do Numpy, calculamos a média dessa lista de valores [15, 5, 10, 25, 20] e armazenamos o resultado na variável media, imprimindo o valor da média na tela.

1.2.1.1.2 - Média ponderada

A média ponderada é uma variação da média aritmética em que cada valor no conjunto de dados é multiplicado por um peso correspondente antes de ser somado. Os pesos atribuídos a cada valor indicam a importância relativa desse valor na média final.

Fórmula da média ponderada: $mp$ = $\frac{p_1 x_1+p_2 x_2+...+p_n x_n}{p_1+p_2+...+ p_n}$, onde $mp$ é a média ponderada, $x_1$, $x_2$, $x_3$, ..., $x_n$ são os valores do conjunto de dados, $p_1$, $p_2$, $p_3$, ..., $p_n$ são os pesos correspondentes a cada valor e $n$ é o número total de observações.

A principal diferença entre a média aritmética e a média ponderada é a inclusão dos pesos na média ponderada. Os pesos indicam a importância relativa de cada valor na média final. Valores com pesos maiores têm uma contribuição maior para o cálculo da média ponderada.

Por exemplo, vamos considerar o conjunto de dados [10, 15, 20] com os respectivos pesos [2, 3, 1]. Para calcular a média ponderada, multiplicamos cada valor pelo peso correspondente, somamos os resultados e dividimos pelo somatório dos pesos:

$mp$ = $\frac{2 . 10 + 3 . 15 + 1 . 20}{2 + 3 + 1}$ = $\frac{20 + 45 + 20}{6}$ = $\frac{85}{6}$ ≈ $14,17$

Portanto, a média ponderada dos valores fornecidos, com os respectivos pesos, é aproximadamente 14,17.

A média ponderada é útil quando certos valores têm maior relevância ou influência nos resultados desejados. Por exemplo, em uma avaliação de desempenho de um aluno, as notas dos exames finais podem ter pesos maiores do que as notas dos trabalhos em grupo. Ao atribuir pesos, podemos refletir a importância relativa desses componentes na média final.

Assim como a média aritmética, a média ponderada é amplamente utilizada em várias áreas, como estatística, finanças, economia e pesquisa de opinião, quando diferentes valores têm importâncias distintas e devem ser considerados na obtenção de uma medida resumida.

Aqui está um exemplo de código em Python usando a biblioteca Numpy para calcular a média ponderada com uma lista de 20 observações desordenadas:

import numpy as np

# Lista de observações
observacoes = [10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105]

# Lista de pesos correspondentes às observações
pesos = [0.1, 0.2, 0.05, 0.15, 0.1, 0.05, 0.05, 0.01, 0.01, 0.03, 0.02, 0.04, 0.03, 0.01, 0.02, 0.02, 0.03, 0.01, 0.02, 0.01]

# Verificar se o número de observações é igual ao número de pesos
if len(observacoes) != len(pesos):
    raise ValueError("O número de observações deve ser igual ao número de pesos")

# Converter as listas para arrays numpy
observacoes = np.array(observacoes)
pesos = np.array(pesos)

# Calcular a média ponderada
media_ponderada = np.average(observacoes, weights=pesos)

# Imprimir o resultado
print("A média ponderada é: {:.2f}".format(media_ponderada))

A média ponderada é: 36.20

Neste exemplo, temos uma lista de 20 observações desordenadas e uma lista correspondente de pesos para cada observação. Usamos a função np.average() do Numpy para calcular a média ponderada, passando as observações como o primeiro argumento e os pesos como o argumento weights. O resultado é armazenado na variável media_ponderada e, em seguida, é impresso na tela.

Certifique-se de que o número de observações seja igual ao número de pesos para que o cálculo seja válido.

1.2.1.1.3 - Média geométrica

A média geométrica é uma medida estatística que é usada para calcular o valor central de um conjunto de números positivos. É obtida pela multiplicação de todos os valores do conjunto e em seguida, elevando o produto à raiz enésima, onde n é o número total de elementos do conjunto. A fórmula para calcular a média geométrica é a seguinte:

$mg = (x_1 . x_2 . x_3 . ... . x_n)^{\frac{1}{n}}$

Onde:

$mg$ é a média geométrica, $x_1$ , $x_2$, $x_3$, ..., $x_n$ são os valores do conjunto de dados e $n$ é o número total de observações.

A média geométrica é especialmente útil quando se lida com grandezas multiplicativas, como taxas de crescimento, rendimentos financeiros ou índices. Ela captura a taxa de crescimento média ao longo de vários períodos, considerando o efeito cumulativo das multiplicações.

Vamos considerar um exemplo com o conjunto de dados [2, 4, 8]. Para calcular a média geométrica, multiplicamos todos os valores e elevamos o resultado à raiz cúbica (já que há três elementos no conjunto):

$mg = (2.4.8)^\frac{1}{3} = 64^\frac{1}{3} ≈ 4$

Portanto, a média geométrica dos valores fornecidos é aproximadamente 4.

É importante destacar que a média geométrica é mais sensível a valores extremos do que a média aritmética. Isso ocorre porque a multiplicação amplifica o efeito desses valores, resultando em uma média geométrica maior ou menor dependendo da direção do valor extremo. Portanto, a média geométrica é mais adequada para dados que seguem uma progressão multiplicativa ou quando se deseja calcular a taxa de crescimento média.

A média geométrica é amplamente utilizada em áreas como finanças, economia, estatística e ciências naturais, onde os valores são multiplicativos ou seguem uma progressão multiplicativa.

Aqui está um exemplo de código em Python usando a biblioteca Numpy para calcular a média geométrica com uma lista de 20 observações desordenadas:

import numpy as np

# Lista de observações
observacoes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71]

# Converter as observações para um array numpy
observacoes = np.array(observacoes)

# Calcular a média geométrica
media_geometrica = np.prod(observacoes) ** (1 / len(observacoes))

# Imprimir o resultado
print("A média geométrica é: {:.2f}".format(media_geometrica))

A média geométrica é: 2.70

Neste exemplo, temos uma lista de 20 observações desordenadas. Usamos a função np.prod() do Numpy para calcular o produto de todos os elementos da lista e, em seguida, usamos a fórmula da média geométrica para calcular a raiz n-ésima do produto, onde n é o número de observações. O resultado é armazenado na variável media_geometrica e, em seguida, é impresso na tela.

Observe que a média geométrica é calculada apenas para valores positivos, pois envolve a multiplicação dos elementos. Certifique-se de ajustar os valores de observação de acordo com o problema que você está resolvendo.

1.2.1.2 - Mediana

A mediana é o valor central em um conjunto de dados ordenados.

Para calcular a mediana, organizamos os dados em ordem crescente e encontramos o valor que divide o conjunto ao meio.

Diferentemente da média, a mediana não é afetada por valores extremos ou discrepantes, o que a torna uma medida robusta para representar a tendência central.

Veremos exemplos práticos de como calcular e interpretar a mediana, especialmente em situações em que a distribuição dos dados não é simétrica.

Exemplo: como calcular a mediana de uma lista de valores usando a biblioteca Numpy:

import numpy as np

# Exemplo de lista de valores
valores = [14, 13, 14, 15, 12, 16, 1750, 24, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30]

# lista ordenada de valores
valores_ordenados = np.sort(valores)

# Imprimir o resultado

# calcular a mediana obtendo o valor que divide o conjunto ao meio
mediana_valores_ordenados = valores_ordenados[len(valores_ordenados) // 2]

# Imprimir a mediana calculada
print("A mediana dos valores é: {:.2f}".format(mediana_valores_ordenados))

# Calcular a mediana usando a função median() do Numpy
mediana = np.median(valores)

# Imprimir a mediana calculada
print("A mediana dos valores é: {:.2f}".format(mediana))

# Calcular a media usando a função mean() do Numpy
media = np.mean(valores)

# Imprimir a média calculada
print("A media dos valores é: {:.2f}".format(media))

A mediana dos valores é: 22.00
A mediana dos valores é: 22.00
A media dos valores é: 103.33

Neste exemplo, temos uma lista com 31 observações. Utilizando a função np.median() do Numpy, calculamos a mediana dessa lista e armazenamos o resultado na variável mediana. Em seguida, imprimimos o valor da mediana na tela.

Observe como o valor da mediana apresenta valor mais próximo ao da maioria dos valores da lista, mas a presença de uma valor destoando dos demais (1750) provocou um grande aumento no valor da média em relação à maioria das observações.

Diferentemente da média, a mediana não é afetada por valores extremos, o que a torna uma medida robusta para representar a tendência central de um conjunto de dados.

1.2.1.3 - Moda

A moda é o valor que ocorre com mais frequência em um conjunto de dados. Ela pode ser usada para identificar os valores mais comuns ou representativos em uma distribuição. Discutiremos como identificar a moda em conjuntos de dados unimodais, bimodais e multimodais. Além disso, exploraremos casos em que não há uma moda clara ou quando os dados são discretos e podem ter múltiplas modas.

A interpretação correta da moda pode fornecer informações valiosas sobre a distribuição e a forma dos dados.

como calcular a moda de uma lista de valores usando a biblioteca SciPy:

from scipy import stats

# Exemplo de lista de valores
valores = [5, 10, 15, 20, 20, 25, 30, 30, 30]

# Calcular a moda usando a função mode do SciPy
moda = stats.mode(valores)

# Imprimir o resultado
print("A moda dos valores é:", moda.mode)

A moda dos valores é: 30

Neste exemplo, temos uma lista de valores [5, 10, 15, 20, 20, 25, 30, 30, 30]. Utilizando a função stats.mode() do SciPy, calculamos a moda dessa lista e armazenamos o resultado na variável moda. O valor da moda é acessado através da propriedade mode(), apontando para uma lista de valores, pois pode haver mais de um valor com a mesma quantidade de ocorrências (multimodal), portanto utilizando apenas o valor do primeiro índice [0], imprimindo a seguir este valor.

Portanto, a moda dos valores [5, 10, 15, 20, 20, 25, 30, 30, 30] é 30. A moda representa o valor que ocorre com maior frequência na lista de valores. No exemplo acima, o valor 30 ocorre três vezes, o que o torna a moda desse conjunto de dados.

Além das medidas de tendência central, é importante compreender as medidas de dispersão, como a variância e o desvio padrão. Essas medidas fornecem informações essenciais sobre a dispersão ou a variabilidade dos dados em relação à média. Assim como nas medidas de tendência central, também vamos explorar a aplicação das medidas de dispersão em diferentes contextos. Exemplos práticos serão fornecidos para ilustrar como a variância e o desvio padrão podem ser usados para:

• Comparar a dispersão dos dados em diferentes grupos.
• Identificar padrões de variabilidade.
• Entender a consistência ou a variabilidade dos resultados em estudos científicos.

Compreender a importância dessas medidas de dispersão ajudará a obter uma visão mais completa e precisa dos dados analisados. Através dessa revisão das medidas de dispersão, incluindo a variância e o desvio padrão, você terá uma compreensão mais aprofundada sobre como essas medidas são calculadas e interpretadas corretamente. Isso lhe dará uma base sólida para continuar explorando os tópicos avançados de estatística que serão abordados no curso, permitindo que você compreenda e analise a variabilidade dos dados de forma precisa e informativa.

1.2.2.1 - Variância

A variância é uma medida que quantifica a dispersão dos valores em torno da média.

Ela mede a média dos quadrados das diferenças entre cada valor e a média do conjunto de dados.

Exploraremos exemplos práticos para entender como calcular a variância, suas propriedades e sua interpretação em diferentes situações. Além disso, discutiremos a relação entre a variância e a distribuição dos dados, bem como as implicações práticas dessa medida.

Exemplo: como calcular a variância de uma lista de valores usando a biblioteca NumPy.

import numpy as np

# Exemplo de lista de valores
valores = [5, 10, 15, 20, 25]

# Calcular a variância usando a função var do NumPy
variancia = np.var(valores)

# Imprimir o resultado
print("A variância dos valores é:", variancia)

A variância dos valores é: 50.0

Neste exemplo, temos uma lista de valores [5, 10, 15, 20, 25]. Utilizando a função np.var() do NumPy, calculamos a variância da lista e armazenamos o resultado na variável variancia, imprimindo em seguida o valor da variância na tela.

A variância é uma medida que quantifica a dispersão dos valores em relação à média, sendo calculada como a média dos quadrados das diferenças entre cada valor e a média do conjunto de dados.

1.2.2.2 - Desvio padrão

O desvio padrão é a raiz quadrada da variância e é uma medida comumente utilizada para expressar a dispersão dos dados, fornecendo uma medida de dispersão que está na mesma escala dos dados originais.

Ao calcular o desvio padrão, podemos interpretá-lo como a média das distâncias entre os valores e a média, considerando a dispersão em torno da média.

Veremos como calcular o desvio padrão e como interpretar essa medida em diferentes cenários, além de discutir sua relação com outras medidas estatísticas.

Exemplo: desvio padrão de uma lista de valores usando a biblioteca NumPy.

import numpy as np

# Exemplo de lista de valores
valores = [5, 10, 15, 20, 25]

# Calcular o desvio padrão usando a função std do NumPy
desvio_padrao = np.std(valores)

# Imprimir o resultado
print("O desvio padrão dos valores é:", desvio_padrao)

O desvio padrão dos valores é: 7.0710678118654755

Neste exemplo, temos uma lista de valores [5, 10, 15, 20, 25]. Utilizando a função np.std() do NumPy, calculamos o desvio padrão dessa lista e armazenamos o resultado na variável desvio_padrao, imprimindo em seguida o valor do desvio padrao.

Portanto, o desvio padrão dos valores [5, 10, 15, 20, 25] é aproximadamente 7,91. O desvio padrão é uma medida que expressa a dispersão dos valores em relação à média. Ele é calculado como a raiz quadrada da variância, fornecendo uma medida de dispersão que está na mesma escala dos dados originais.

A probabilidade é uma medida numérica que representa a chance ou a frequência relativa de ocorrência de um evento em relação ao conjunto de todos os eventos possíveis. Ela fornece uma maneira de quantificar a incerteza e a aleatoriedade em um experimento, sendo expressa em uma escala de 0 a 1, onde 0 significa impossibilidade absoluta, que o evento é impossível, e 1 significa certeza absoluta, que o evento é certo. Um evento com probabilidade 0 não ocorrerá, enquanto um evento com probabilidade 1 ocorrerá com certeza.

A probabilidade de um evento pode ser determinada de diferentes maneiras, dependendo da natureza do experimento e das informações disponíveis. Existem três abordagens principais para determinar a probabilidade: abordagem clássica, abordagem frequentista e abordagem subjetiva.

A abordagem clássica, também conhecida como probabilidade teórica, é aplicada quando todos os resultados possíveis do experimento são igualmente prováveis. Nesse caso, a probabilidade de um evento é calculada dividindo o número de resultados favoráveis pelo número total de resultados possíveis.

A abordagem frequentista, também conhecida como probabilidade empírica, é baseada na observação de frequências relativas. A probabilidade de um evento é calculada como a proporção de vezes em que o evento ocorre em um grande número de repetições do experimento.

A abordagem subjetiva é baseada nas crenças e nas informações disponíveis de um indivíduo. Nessa abordagem, a probabilidade é uma medida subjetiva de confiança ou grau de crença na ocorrência de um evento.

A probabilidade possui várias propriedades, como a aditividade (a probabilidade da união de eventos é igual à soma das probabilidades dos eventos individuais), a multiplicatividade (a probabilidade da interseção de eventos independentes é igual ao produto das probabilidades) e a complementaridade (a probabilidade do evento complementar é igual a 1 menos a probabilidade do evento).

A teoria da probabilidade é amplamente aplicada em diversas áreas, como estatística, ciência, engenharia, finanças, entre outras, para análise e tomada de decisões com base na incerteza e no risco.

Os conceitos fundamentais de probabilidade desempenham um papel crucial na estatística e são de suma importância na correta compreensão e aplicação dos métodos estatísticos.

A compreensão dos conceitos fundamentais de probabilidade é essencial para aprofundarmos nossos conhecimentos em estatística avançada, uma vez que muitos dos métodos e técnicas estatísticas são baseados em princípios probabilísticos. Portanto, esse estudo introdutório nos fornecerá a base necessária para explorar tópicos mais avançados, como inferência estatística, modelos probabilísticos e técnicas de amostragem, ampliando assim nossa compreensão e habilidades na análise de dados.

inicialmente apresentaremos os diferentes tipos de probabilidade:

• Probabilidade Clássica: também conhecida como probabilidade à priori, é baseada na contagem de casos igualmente prováveis. Por exemplo, ao lançar um dado justo de seis faces, a probabilidade de obter qualquer número é 1/6.
• Probabilidade Empírica: probabilidade determinada pela frequência relativa de um evento em um grande número de repetições de um experimento. Por exemplo, lançar uma moeda várias vezes e contar a proporção de vezes que "cara" ocorre.
• Probabilidade Condicional: probabilidade de um evento ocorrer, dado que outro evento já ocorreu. É denotada por $P(A|B)$, onde $A$ e $B$ são eventos. Por exemplo, a probabilidade de chover, dado que as nuvens estão escuras.

A probabilidade é um campo fundamental da teoria estatística e envolve vários conceitos-chave

A seguir apresentaremos dois importantes conceitos de probabilidade:

• Espaço Amostral: conjunto de todos os resultados possíveis de um experimento. Por exemplo, ao lançar uma moeda, o espaço amostral é composto pelos resultados "cara" e "coroa".
• Evento: subconjunto do espaço amostral representando um conjunto de resultados específicos. Por exemplo, o evento de obter "cara" ao lançar uma moeda.

Em seguida, discutiremos as diferentes interpretações da probabilidade, que oferecem perspectivas distintas sobre como compreender e quantificar a incerteza. Existem diferentes interpretações da probabilidade que refletem perspectivas distintas sobre como compreender e quantificar a incerteza. Essas interpretações fornecem abordagens filosóficas e práticas para lidar com a probabilidade.

Entre essas interpretações, destacam-se:

• Interpretação Frequentista: essa interpretação define a probabilidade como a frequência relativa de um evento em um grande número de repetições de um experimento. Segundo a abordagem frequentista, a probabilidade é objetiva e baseada na observação empírica de eventos repetidos. Por exemplo, a probabilidade de obter "cara" ao lançar uma moeda justa é 0.5, porque, em muitos lançamentos, espera-se que metade dos resultados seja "cara". Essa interpretação é amplamente aplicada em experimentos repetíveis, como jogos de azar e pesquisas estatísticas.
• Interpretação Subjetiva: nessa interpretação, a probabilidade é vista como uma medida subjetiva da crença ou grau de confiança de um indivíduo em relação a um evento ocorrer. As probabilidades são atribuídas com base em conhecimentos prévios, crenças, experiências pessoais e julgamentos subjetivos. Cada pessoa pode ter diferentes probabilidades subjetivas para o mesmo evento, dependendo de suas informações e perspectivas individuais. Essa interpretação é comumente aplicada em situações em que não é possível obter dados empíricos ou quando a incerteza é baseada em julgamentos individuais.
• Interpretação Axiomática ou Clássica: essa interpretação se baseia em um conjunto de axiomas matemáticos que descrevem as propriedades da probabilidade. A probabilidade é tratada como uma medida matemática que segue certas regras e princípios, independentemente de sua interpretação filosófica subjacente. Essa interpretação é amplamente usada na teoria da probabilidade e fornece uma estrutura matemática sólida para a análise probabilística.
• Interpretações modernas: são abordagens como a probabilidade bayesiana, que combina informações à priori (conhecimentos prévios), atualizando com dados observados a probabilidade de eventos (probabilidades a posteriori). A probabilidade bayesiana é especialmente útil em situações em que novas evidências podem alterar as crenças iniciais sobre um evento.

Cada interpretação da probabilidade tem suas vantagens e limitações, e a escolha da interpretação depende do contexto e dos objetivos da análise probabilística. É importante reconhecer que a interpretação da probabilidade pode variar entre os campos da estatística, da ciência e da filosofia, e diferentes abordagens podem ser adequadas em diferentes situações.

Em seguida, examinaremos as principais regras e propriedades da probabilidade:

• Regra da Adição: também conhecida como princípio da soma, é fundamental para calcularmos a probabilidade da ocorrência de pelo menos um de dois eventos mutuamente exclusivos. Essa regra estabelece que a probabilidade da ocorrência de pelo menos um desses eventos é igual à soma das probabilidades individuais de cada evento. A probabilidade da união de dois eventos $A$ e $B$ é dada por $P(A ∪ B) = P(A)+P(B)$.
• Regra da multiplicação: também conhecida como princípio do produto, é aplicada para calcular a probabilidade conjunta de dois eventos eventos independentes. Essa regra estabelece que a probabilidade da ocorrência simultânea de dois eventos independentes é igual ao produto das probabilidades individuais de cada evento. A probabilidade da interseção de dois eventos $A$ e $B$ é dada por $P(A ∩ B) = P(A).P(B)$.
• Regra da complementaridade: estabelece que a probabilidade de um evento ocorrer somada à probabilidade de seu complemento ocorrer é igual a 1, significando que a probabilidade total de ocorrer um evento ou seu complemento é certa. Matematicamente, $P(A) + P(A') = 1$, onde $A'$ representa o complemento de $A$.
• Regra da probabilidade condicional: probabilidade de um evento A ocorrer dado que outro evento B já ocorreu. A regra da probabilidade condicional é expressa por P(A|B) = P(A ∩ B) / P(B), onde P(A|B) é a probabilidade condicional de A dado B.
• Regra da probabilidade total: usada quando um evento pode ocorrer de várias maneiras, cada uma com uma probabilidade associada. A probabilidade total de um evento A é dada pela soma das probabilidades de A ocorrer em cada uma dessas maneiras. Matematicamente, P(A) = ∑[P(A|B) * P(B)], onde a soma é realizada para todos os eventos mutuamente exclusivos B que cobrem todo o espaço amostral.
• Regra de Bayes: permite atualizar probabilidades com base em informações adicionais. É usada para calcular a probabilidade de um evento A ocorrer dado que outro evento B já ocorreu. A fórmula da regra de Bayes é P(A|B) = [P(B|A) * P(A)] / P(B), onde P(A|B) é a probabilidade condicional de A dado B.

Ao compreender e dominar as regras e propriedades da probabilidade, estaremos preparados para formular e construir modelos estatísticos sólidos. Esses modelos são utilizados para descrever e analisar fenômenos aleatórios e incertos, permitindo-nos realizar inferências estatísticas e tomar decisões informadas com base em dados observados.

Esses são apenas alguns dos conceitos fundamentais da teoria da probabilidade. A partir desses conceitos, podemos explorar outros tópicos avançados, como distribuições de probabilidade, teoremas de limite central, teoria das probabilidades condicionais e probabilidade bayesiana.

1.2.3.1 - Probabilidade Clássica

A Probabilidade Clássica, também conhecida como probabilidade teórica ou probabilidade a priori, é uma abordagem para determinar a probabilidade de um evento com base na suposição de que todos os resultados possíveis são igualmente prováveis. Essa abordagem é aplicada quando temos um conjunto finito de resultados possíveis e cada resultado tem a mesma chance de ocorrer.

A Probabilidade Clássica é frequentemente usada em situações de experimentos teóricos ou ideais, onde é possível listar e contar todos os resultados possíveis com igual chance de ocorrência.

Para calcular a probabilidade clássica de um evento, é necessário seguir os seguintes passos:

• Identificar o espaço amostral: o espaço amostral é o conjunto de todos os resultados possíveis do experimento. É importante ter uma compreensão clara dos resultados possíveis.
• Identificar o evento de interesse: o evento é um subconjunto do espaço amostral que descreve uma ou mais condições ou resultados específicos que estamos interessados em calcular a probabilidade.
• Calcular a probabilidade: o probabilidade clássica é calculada dividindo o número de resultados favoráveis ao evento pelo número total de resultados possíveis.

A fórmula para calcular a probabilidade clássica é: $Probabilidade = \frac{favoraveis}{possiveis}$, onde $favoraveis$ é o número de resultados favoráveis e $possiveis$ é o número total de resultados possíveis.

É importante ressaltar que a probabilidade clássica pressupõe que todos os resultados possíveis são equiprováveis, ou seja, cada resultado tem a mesma chance de ocorrer. Essa suposição nem sempre é válida na prática, mas em experimentos teóricos bem definidos e equilibrados, a probabilidade clássica é amplamente utilizada.

Vamos supor que temos uma moeda justa, onde os resultados possíveis são cara (C) ou coroa (K). Queremos calcular a probabilidade de obter cara em um lançamento.

# Importar a biblioteca random
import random

# Definir o espaço amostral e o evento de interesse
espaco_amostral = ['C', 'K']
evento_cara = 'C'

# Simular o lançamento da moeda várias vezes
num_lancamentos = 1000
contador_cara = 0

for _ in range(num_lancamentos):
    resultado = random.choice(espaco_amostral)
    if resultado == evento_cara:
        contador_cara += 1

# Calcular a probabilidade clássica
probabilidade = contador_cara / num_lancamentos

# Imprimir o resultado
print("A probabilidade de obter cara é:", probabilidade)

A probabilidade de obter cara é: 0.5

Nesse exemplo, simulamos o lançamento da moeda 1000 vezes e contamos quantas vezes obtivemos o resultado cara. Em seguida, calculamos a probabilidade dividindo o número de vezes que obtivemos cara pelo número total de lançamentos, colaborando no entendimento do conceito de probabilidade Clássica e como calcular a probabilidade em situações em que todos os resultados possíveis são igualmente prováveis!

1.2.3.2 - Probabilidade Empírica

A Probabilidade Empírica, também conhecida como probabilidade experimental, é uma abordagem para determinar a probabilidade de um evento com base em dados observados ou coletados a partir de experimentos ou eventos reais. Diferente da probabilidade clássica, a probabilidade empírica é baseada em evidências empíricas e não pressupõe que todos os resultados possíveis sejam igualmente prováveis.

A Probabilidade Empírica é aplicada quando temos dados ou observações de eventos passados e queremos usar essas informações para estimar a probabilidade de eventos futuros sem fazer suposições teóricas.

Para calcular a probabilidade empírica de um evento, é necessário seguir os seguintes passos:

• Coletar os dados: é necessário coletar dados relevantes sobre o evento de interesse. Isso pode ser feito por meio de observação direta, experimentos ou análise de dados históricos.
• Contar os resultados favoráveis: com base nos dados coletados, é necessário contar o número de vezes que o evento de interesse ocorreu.
• Calcular a probabilidade: a probabilidade empírica é calculada dividindo o número de resultados favoráveis pelo número total de observações.

A fórmula para calcular a probabilidade empírica é: $Probabilidade = \frac{favoraveis}{observacoes}$, onde $favoraveis$ é o número de resultados favoráveis e $observacoes$ é o número total de observações.

É importante ressaltar que a probabilidade empírica é baseada em evidências empíricas limitadas e está sujeita a flutuações e incertezas devido à natureza dos dados coletados. Quanto maior for o tamanho da amostra ou o número de observações, mais confiável será a estimativa da probabilidade.

Vamos supor que temos uma caixa com bolas vermelhas e azuis. Queremos calcular a probabilidade empírica de retirar uma bola vermelha da caixa com base em uma série de experimentos.

# Importar a biblioteca random
import random

# Definir a caixa com bolas
caixa = ['vermelha', 'azul']

# Realizar uma série de experimentos
num_experimentos = 100
contador_vermelha = 0

for _ in range(num_experimentos):
    bola = random.choice(caixa)
    if bola == 'vermelha':
        contador_vermelha += 1

# Calcular a probabilidade empírica
probabilidade_empirica = contador_vermelha / num_experimentos

# Imprimir o resultado
print("A probabilidade empírica de retirar uma bola vermelha é:", probabilidade_empirica)

A probabilidade empírica de retirar uma bola vermelha é: 0.59

Nesse exemplo, simulamos uma série de experimentos em que retiramos uma bola da caixa (com reposição) e contamos quantas vezes obtivemos uma bola vermelha. Em seguida, calculamos a probabilidade empírica dividindo o número de vezes que obtivemos uma bola vermelha pelo número total de experimentos.

1.2.3.3 - Probabilidade condicional

A Probabilidade Condicional é uma medida de probabilidade que descreve a probabilidade de ocorrência de um evento A dado que outro evento B já ocorreu. Ela permite que levemos em consideração informações adicionais ou restrições ao calcular a probabilidade de um evento.

A probabilidade condicional é denotada como $P(A|B)$, onde $A$ e $B$ são eventos, e lê-se "a probabilidade de A dado B". A fórmula para calcular a probabilidade condicional é:

$P(A|B) = \frac{P(A e B)}{P(B)}$

Aqui estão alguns conceitos-chave relacionados à probabilidade condicional:

• Evento $A$: é o evento cuja probabilidade queremos calcular, dado que o evento B ocorreu.
• Evento $B$: é o evento que já ocorreu ou que estamos considerando como dado. É a base para calcular a probabilidade condicional.
• $P(A e B)$: representa a probabilidade conjunta de ocorrência dos eventos $A$ e $B$, ou seja, a probabilidade de ambos os eventos ocorrerem simultaneamente.
• $P(B)$: representa a probabilidade do evento B ocorrer.

A probabilidade condicional é útil para analisar situações em que a ocorrência de um evento está relacionada ou depende da ocorrência de outro evento. Ela nos permite ajustar nossas estimativas de probabilidade com base nas informações disponíveis.

Vamos considerar um exemplo em que temos uma urna com bolas vermelhas e azuis. Queremos calcular a probabilidade de tirar uma bola vermelha da urna, dado que a primeira bola tirada foi azul.

# Importar a biblioteca random
import random

# Definir a urna com bolas
urna = ['vermelha', 'azul', 'azul']

# Realizar a primeira retirada
primeira_bola = random.choice(urna)

# Verificar se a primeira bola é azul
if primeira_bola == 'azul':
    # Retirar uma segunda bola da urna
    segunda_bola = random.choice(urna)
    if segunda_bola == 'vermelha':
        # Calcular a probabilidade condicional P(A|B)
        prob_condicional = 1.0
    else:
        prob_condicional = 0.0
else:
    prob_condicional = 0.0

# Imprimir o resultado
print("A probabilidade condicional de tirar uma bola vermelha dado que a primeira bola foi azul é:", prob_condicional)

A probabilidade condicional de tirar uma bola vermelha dado que a primeira bola foi azul é: 0.0

Nesse exemplo, simulamos a retirada de duas bolas da urna com reposição. Se a primeira bola retirada for azul, verificamos a cor da segunda bola. Se a segunda bola for vermelha, a probabilidade condicional é igual a 1 (certeza de que a segunda bola é vermelha). Caso contrário, a probabilidade condicional é igual a 0 (impossibilidade de a segunda bola ser vermelha).

1.2.3.4 - Espaço Amostral

O espaço amostral é um dos conceitos fundamentais da teoria das probabilidades. Ele representa o conjunto de todos os resultados possíveis de um experimento aleatório. Em outras palavras, o espaço amostral é o conjunto de todos os eventos elementares que podem ocorrer em um experimento.

Vamos considerar um exemplo simples: lançar um dado comum de seis faces. O espaço amostral nesse caso seria o conjunto {1, 2, 3, 4, 5, 6}, que representa todos os resultados possíveis do lançamento do dado. Cada número nesse conjunto é um evento elementar, ou seja, um resultado individual que pode ocorrer.

O espaço amostral pode ser finito, como no exemplo do dado, em que temos um número limitado de resultados possíveis. No entanto, também pode ser infinito, como no caso de lançar uma moeda infinitas vezes, em que o espaço amostral seria o conjunto de todos os resultados possíveis (cara ou coroa) repetidos infinitamente.

É importante ressaltar que o espaço amostral deve ser bem definido e abranger todos os resultados possíveis do experimento. Ele é a base para a análise de probabilidades, pois todos os eventos e suas respectivas probabilidades são derivados do espaço amostral.

Além do espaço amostral, outros conceitos importantes relacionados à teoria das probabilidades incluem eventos, probabilidade, combinação de eventos e cálculo de probabilidades. Todos esses conceitos juntos nos permitem quantificar e estudar a incerteza associada a um determinado fenômeno aleatório.

import numpy as np

# Definindo o espaço amostral
espaco_amostral = np.array([1, 2, 3, 4, 5, 6])

# Imprimindo o espaço amostral
print("Espaço Amostral:", espaco_amostral)

Espaço Amostral: [1 2 3 4 5 6]

Neste exemplo, usamos a biblioteca numpy para criar um array com os elementos do espaço amostral, que são os números de 1 a 6, representando as faces do dado. Em seguida, imprimimos o espaço amostral na tela.

Lembrando que o espaço amostral pode ser personalizado de acordo com o contexto do problema. Neste caso, consideramos o espaço amostral de um dado comum, mas você pode ajustar o código para outros experimentos aleatórios, modificando os valores dentro do array espaco_amostral.

1.2.3.5 - Eventos

Um evento é um conjunto de resultados possíveis em um experimento aleatório. Em outras palavras, é um subconjunto do espaço amostral. Podemos dizer que um evento ocorre quando um ou mais resultados do espaço amostral são observados.

Os eventos podem ser classificados em diferentes tipos:

• Evento Simples: é um evento que contém apenas um resultado específico. Por exemplo, ao lançar um dado, obter o resultado "4" é um evento simples.
• Evento Composto: é um evento que contém mais de um resultado possível. Por exemplo, ao lançar um dado, obter um número par (2, 4 ou 6) é um evento composto.
• Evento Mutuamente Exclusivo: são eventos que não podem ocorrer simultaneamente. Se um evento acontece, o outro evento não pode ocorrer ao mesmo tempo. Por exemplo, ao lançar um dado, obter um número par e obter um número ímpar são eventos mutuamente exclusivos.
• Evento Independente: são eventos cuja ocorrência ou não ocorrência de um evento não afeta a probabilidade de ocorrência do outro evento. Por exemplo, ao lançar uma moeda, obter "cara" e obter "coroa" são eventos independentes.

1.2.3.5.1 - Evento Simples

Um evento simples contém apenas um resultado específico em um experimento aleatório. Em outras palavras, é um evento que ocorre quando um resultado específico do espaço amostral é observado. Os eventos simples são indivisíveis, pois não podem ser decompostos em subeventos menores.

Vamos considerar um experimento de lançamento de um dado de seis faces, onde queremos calcular a probabilidade de obter um resultado específico, como "4".

# Importando a biblioteca random para gerar números aleatórios
import random

# Definindo a função para simular o lançamento de um dado
def lancamento_dado():
    return random.randint(1, 6)

# Definindo o número de experimentos
num_experimentos = 1000

# Contador para o número de vezes que o evento "4" ocorre
num_evento_4 = 0

# Realizando os experimentos
for _ in range(num_experimentos):
    resultado = lancamento_dado()
    if resultado == 4:
        num_evento_4 += 1

# Calculando a probabilidade do evento "4"
probabilidade_4 = num_evento_4 / num_experimentos

# Imprimindo o resultado
print("Probabilidade de obter o resultado 4:", probabilidade_4)

Probabilidade de obter o resultado 4: 0.177

Neste exemplo, estamos simulando o lançamento de um dado em 1000 experimentos. A função lancamento_dado() retorna um número aleatório entre 1 e 6, simulando o lançamento do dado. Em cada experimento, verificamos se o resultado é igual a 4 e incrementamos o contador num_evento_4 se for o caso. Por fim, calculamos a probabilidade dividindo o número de vezes que o evento "4" ocorre pelo número total de experimentos.

É importante ressaltar que os eventos podem ser combinados usando operações de conjuntos, como união, interseção e complementaridade, para criar eventos mais complexos.

1.2.3.5.2 - Evento Composto

Um evento composto é um evento que ocorre quando dois ou mais resultados específicos de um experimento aleatório são observados. Em outras palavras, é a combinação de dois ou mais eventos simples. Os eventos compostos podem ser divididos em dois tipos principais: eventos unidos por "E" (interseção) e eventos unidos por "OU" (união).

• Evento Composto com "E" (Interseção): O evento ocorre quando ambos os eventos individuais ocorrem simultaneamente.
• Evento Composto com "OU" (União): O evento ocorre quando pelo menos um dos eventos individuais ocorre.

Vamos considerar um experimento de lançamento de uma moeda e um dado, onde queremos calcular a probabilidade de obter "cara" na moeda e "5" no dado. Faremos isso usando o operador lógico "E" para a interseção dos eventos.

# Importando a biblioteca random para gerar números aleatórios
import random

# Definindo a função para simular o lançamento de uma moeda
def lancamento_moeda():
    return random.choice(['cara', 'coroa'])

# Definindo a função para simular o lançamento de um dado
def lancamento_dado():
    return random.randint(1, 6)

# Definindo o número de experimentos
num_experimentos = 1000

# Contador para o número de vezes que o evento composto ocorre
num_evento_composto = 0

# Realizando os experimentos
for _ in range(num_experimentos):
    resultado_moeda = lancamento_moeda()
    resultado_dado = lancamento_dado()
    if resultado_moeda == 'cara' and resultado_dado == 5:
        num_evento_composto += 1

# Calculando a probabilidade do evento composto
probabilidade_evento_composto = num_evento_composto / num_experimentos

# Imprimindo o resultado
print("Probabilidade de obter 'cara' na moeda e '5' no dado:", probabilidade_evento_composto)

Probabilidade de obter 'cara' na moeda e '5' no dado: 0.087

Neste exemplo, estamos simulando o lançamento de uma moeda e um dado em 1000 experimentos. A função lancamento_moeda() retorna aleatoriamente "cara" ou "coroa" para simular o lançamento da moeda, e a função lancamento_dado() retorna um número aleatório entre 1 e 6 para simular o lançamento do dado. Em cada experimento, verificamos se o resultado da moeda é "cara" e o resultado do dado é 5, e incrementamos o contador num_evento_composto se ambos os eventos ocorrerem simultaneamente. Por fim, calculamos a probabilidade dividindo o número de vezes que o evento composto ocorre pelo número total de experimentos.

1.2.3.5.3 - Eventos Mutuamente Exclusivo

Dois eventos são considerados mutuamente exclusivos se eles não puderem ocorrer simultaneamente, ou seja, a ocorrência de um evento exclui a ocorrência do outro. Matematicamente, dois eventos $A$ e $B$ são mutuamente exclusivos se a interseção entre eles for vazia, ou seja, $A ∩ B = ∅$. Isso significa que se um evento ocorrer, o outro não pode ocorrer ao mesmo tempo.

Vamos considerar dois eventos: "obter um número par" e "obter um número ímpar" ao lançar um dado. Vamos calcular a probabilidade de ocorrer um dos eventos mutuamente exclusivos usando um exemplo de código Python.

# Importando a biblioteca random para gerar números aleatórios
import random

# Definindo a função para simular o lançamento de um dado
def lancamento_dado():
    return random.randint(1, 6)

# Definindo o número de experimentos
num_experimentos = 1000

# Contadores para o número de vezes que cada evento ocorre
num_par = 0
num_impar = 0

# Realizando os experimentos
for _ in range(num_experimentos):
    resultado = lancamento_dado()
    if resultado % 2 == 0:
        num_par += 1
    else:
        num_impar += 1

# Calculando a probabilidade de um dos eventos ocorrer
probabilidade_mutuamente_exclusivo = (num_par + num_impar) / num_experimentos

# Imprimindo os resultados
print("Probabilidade de ocorrer um número par ou ímpar:", probabilidade_mutuamente_exclusivo)
print("Probabilidade de ocorrer um número par:", num_par / num_experimentos)
print("Probabilidade de ocorrer um número ímpar:", num_impar / num_experimentos)

Probabilidade de ocorrer um número par ou ímpar: 1.0
Probabilidade de ocorrer um número par: 0.516
Probabilidade de ocorrer um número ímpar: 0.484

Neste exemplo, estamos simulando o lançamento de um dado em 1000 experimentos. A função lancamento_dado() retorna um número aleatório entre 1 e 6 para simular o lançamento do dado. Em cada experimento, verificamos se o resultado é par ou ímpar e incrementamos os contadores num_par e num_impar de acordo. Por fim, calculamos a probabilidade de ocorrer um dos eventos mutuamente exclusivos dividindo o número de vezes que um dos eventos ocorre pelo número total de experimentos.

1.2.3.5.4 - Eventos Independentes

Dois eventos $A$ e $B$ são considerados independentes se a ocorrência (ou não ocorrência) de um evento não afeta a probabilidade do outro evento ocorrer. Em outras palavras, a probabilidade de ambos os eventos A e B ocorrerem é o produto das probabilidades individuais de cada evento. Matematicamente, dois eventos $A$ e $B$ são independentes se $P(A ∩ B) = P(A) × P(B)$.

Vamos considerar dois eventos: "obter cara em uma moeda" e "obter um número par em um dado". Vamos calcular a probabilidade de ambos os eventos ocorrerem simultaneamente usando um exemplo de código Python.

# Importando a biblioteca random para gerar números aleatórios
import random

# Definindo a função para simular o lançamento de uma moeda
def lancamento_moeda():
    return random.choice(['cara', 'coroa'])

# Definindo a função para simular o lançamento de um dado
def lancamento_dado():
    return random.randint(1, 6)

# Definindo o número de experimentos
num_experimentos = 1000

# Contadores para o número de vezes que ambos os eventos ocorrem
num_cara_e_par = 0

# Realizando os experimentos
for _ in range(num_experimentos):
    resultado_moeda = lancamento_moeda()
    resultado_dado = lancamento_dado()
    if resultado_moeda == 'cara' and resultado_dado % 2 == 0:
        num_cara_e_par += 1

# Calculando a probabilidade de ambos os eventos ocorrerem
probabilidade_independente = num_cara_e_par / num_experimentos

# Imprimindo o resultado
print("Probabilidade de obter cara e número par:", probabilidade_independente)

Probabilidade de obter cara e número par: 0.241

Neste exemplo, estamos simulando o lançamento de uma moeda e um dado em 1000 experimentos. A função lancamento_moeda() retorna "cara" ou "coroa" para simular o lançamento da moeda, e a função lancamento_dado() retorna um número aleatório entre 1 e 6 para simular o lançamento do dado. Em cada experimento, verificamos se o resultado da moeda é "cara" e se o resultado do dado é par. Se ambos os eventos ocorrerem, incrementamos o contador num_cara_e_par. Por fim, calculamos a probabilidade de ambos os eventos ocorrerem dividindo o número de vezes que isso acontece pelo número total de experimentos.

1.2.3.6 - Interpretação Frequentista

A interpretação frequentista é uma das principais interpretações da probabilidade e baseia-se na frequência relativa de ocorrência de um evento em um grande número de experimentos repetidos. Segundo essa interpretação, a probabilidade de um evento é definida como a proporção de vezes que o evento ocorre em relação ao número total de experimentos.

De acordo com a interpretação frequentista, a probabilidade é uma propriedade objetiva do mundo físico e está diretamente relacionada à frequência com que um evento ocorre em uma série infinita de observações. Essa interpretação se baseia na ideia de que, à medida que o número de experimentos aumenta, a frequência relativa de ocorrência de um evento se aproxima de um valor constante, que é a probabilidade do evento.

Principais pontos da interpretação frequentista:

• Experimentos repetidos: a interpretação frequentista considera a repetição de um experimento em condições idênticas para obter uma série de resultados.
• Frequência relativa: a probabilidade é definida como a frequência relativa de ocorrência de um evento em relação ao número total de experimentos.
• Estabilidade no longo prazo: a interpretação frequentista assume que, à medida que o número de experimentos aumenta, a frequência relativa de um evento se aproxima de um valor constante, que representa a probabilidade do evento.
• Probabilidade como proporção: na interpretação frequentista, a probabilidade é expressa como uma proporção entre o número de vezes que um evento ocorre e o número total de experimentos.
• Limitações: essa interpretação requer a possibilidade de repetir um experimento em condições idênticas e não é aplicável a eventos únicos ou não repetíveis.

A interpretação frequentista é amplamente utilizada em estatística e na análise de dados, especialmente quando se trata de experimentos repetidos em que a probabilidade pode ser estimada com base na frequência relativa dos resultados observados.

É importante ressaltar que outras interpretações da probabilidade, como a interpretação subjetiva e a interpretação proporcional, também são utilizadas em diferentes contextos e abordagens teóricas.

1.2.3.6.1 - Experimentos repetidos

Experimentos repetidos referem-se à realização de um mesmo experimento várias vezes, com o objetivo de observar a frequência com que um evento ocorre ao longo dessas repetições. Isso está relacionado à interpretação frequentista da probabilidade, que se baseia na ideia de que a probabilidade de um evento é igual à frequência relativa com que ele ocorre em um grande número de experimentos repetidos. Vamos detalhar essa abordagem e fornecer um exemplo de código Python para ilustrar o conceito.

Na interpretação frequentista da probabilidade, consideramos um experimento que pode ser repetido um grande número de vezes, e o objetivo é observar a frequência com que um evento específico ocorre em relação ao número total de repetições. A ideia é que, à medida que o número de repetições aumenta, a frequência relativa do evento converge para a probabilidade do evento.

Para realizar experimentos repetidos, precisamos definir um procedimento experimental bem definido, no qual cada repetição do experimento seja idêntica às demais. Em seguida, executamos o experimento um grande número de vezes e registramos quantas vezes o evento de interesse ocorre.

A interpretação frequentista é amplamente utilizada em experimentos científicos e estudos estatísticos, pois nos permite fazer inferências sobre a probabilidade de eventos com base na observação empírica de sua frequência relativa em experimentos repetidos.

Vamos considerar um exemplo simples para ilustrar experimentos repetidos usando Python. Suponha que queremos simular o lançamento de um dado de seis faces e contar quantas vezes um número específico, como o número 4, aparece em um grande número de lançamentos. Usaremos a biblioteca random do Python para simular o lançamento do dado.

import random

def experimento_lancamento_dado():
    # Simula o lançamento de um dado de seis faces
    return random.randint(1, 6)

def experimentos_repetidos(n, evento):
    # Realiza n experimentos repetidos
    ocorrencias = 0
    for _ in range(n):
        resultado = experimento_lancamento_dado()
        if resultado == evento:
            ocorrencias += 1
    return ocorrencias

# Configurações do experimento
num_repeticoes = 10000
numero_evento = 4

# Realiza os experimentos repetidos
ocorrencias_evento = experimentos_repetidos(num_repeticoes, numero_evento)

# Calcula a frequência relativa do evento
frequencia_relativa = ocorrencias_evento / num_repeticoes

# Imprime o resultado
print(f"A frequência relativa do número {numero_evento} é de {frequencia_relativa:.4f}")

A frequência relativa do número 4 é de 0.1663

Nesse exemplo, realizamos 10.000 lançamentos do dado e contamos quantas vezes o número 4 apareceu. Em seguida, calculamos a frequência relativa dividindo o número de ocorrências do evento pelo número total de repetições. O resultado é impresso na tela.

Esse é apenas um exemplo básico para ilustrar como realizar experimentos repetidos e calcular a frequência relativa de um evento específico. Em problemas mais complexos, podem ser necessárias abordagens estatísticas mais avançadas para analisar os resultados dos experimentos repetidos e fazer inferências sobre a probabilidade dos eventos.

1.2.3.6.2 - Frequência relativa

Frequência relativa é um conceito importante na estatística e probabilidade que se refere à proporção de vezes em que um evento ocorre em relação ao número total de observações ou experimentos realizados. É uma medida empírica que nos permite estimar a probabilidade de um evento com base nos dados coletados. Vamos detalhar esse conceito e fornecer um exemplo de código Python para calcular a frequência relativa.

A frequência relativa é uma medida estatística que expressa a proporção de ocorrências de um evento em relação ao número total de observações ou experimentos. Ela é calculada dividindo-se o número de vezes em que o evento ocorre pelo número total de observações ou experimentos.

A frequência relativa é uma estimativa empírica da probabilidade de um evento. Quanto mais observações ou experimentos são realizados, maior é a precisão da estimativa. Se um evento tiver uma frequência relativa estável ao longo de um grande número de observações, podemos interpretar essa frequência como uma estimativa da probabilidade do evento.

A frequência relativa é expressa como uma proporção ou um valor decimal entre 0 e 1, ou como uma porcentagem entre 0% e 100%. Se um evento ocorre em todas as observações ou experimentos, sua frequência relativa é igual a 1 (ou 100%). Se um evento nunca ocorre, sua frequência relativa é igual a 0 (ou 0%).

Aqui está um exemplo simples de como calcular a frequência relativa usando Python. Suponha que temos uma lista de observações de um evento e queremos calcular a frequência relativa desse evento.

def calcular_frequencia_relativa(observacoes, evento):
    ocorrencias = observacoes.count(evento)
    total_observacoes = len(observacoes)
    frequencia_relativa = ocorrencias / total_observacoes
    return frequencia_relativa

# Exemplo de observações
observacoes = [1, 2, 3, 1, 4, 1, 5, 1, 6, 1]

# Evento a ser calculado a frequência relativa
evento = 1

# Cálculo da frequência relativa
frequencia = calcular_frequencia_relativa(observacoes, evento)

# Imprimir o resultado
print(f"A frequência relativa do evento {evento} é de {frequencia:.2f}")

A frequência relativa do evento 1 é de 0.50

Neste exemplo, temos uma lista de observações [1, 2, 3, 1, 4, 1, 5, 1, 6, 1] e queremos calcular a frequência relativa do evento "1". A função calcular_frequencia_relativa recebe a lista de observações e o evento desejado, conta o número de ocorrências do evento na lista e divide pelo total de observações para obter a frequência relativa. O resultado é impresso na tela com duas casas decimais.

Lembre-se de que a frequência relativa é uma estimativa da probabilidade do evento com base nos dados observados. Quanto mais observações forem feitas, maior será a confiabilidade da estimativa.

1.2.3.6.3 - Estabilidade no longo prazo

Estabilidade no longo prazo é um conceito importante na probabilidade e estatística que se refere à consistência das estimativas de probabilidade ou frequência relativa à medida que o número de observações aumenta. Nesse contexto, "longo prazo" significa realizar um grande número de observações ou repetir um experimento muitas vezes. Vamos detalhar esse conceito e fornecer um exemplo de código Python para demonstrar a estabilidade no longo prazo.

A estabilidade no longo prazo é um princípio fundamental na probabilidade e estatística, relacionado à consistência das estimativas de probabilidade ou frequência relativa à medida que aumentamos o número de observações. O princípio afirma que, à medida que realizamos um número cada vez maior de observações ou repetimos um experimento muitas vezes, as estimativas de probabilidade ou frequência relativa se aproximam cada vez mais do valor verdadeiro.

Em termos simples, isso significa que a probabilidade estimada de um evento ou a frequência relativa desse evento tende a se estabilizar e se aproximar da probabilidade real à medida que coletamos mais dados. Por exemplo, se estivermos lançando uma moeda justa e registrando a frequência relativa de caras, à medida que o número de lançamentos aumenta, a frequência relativa se aproximará cada vez mais de 0,5, que é a probabilidade verdadeira de obter cara em um lançamento justo.

Esse conceito é importante porque nos permite fazer inferências mais precisas com base em um grande número de observações. Quanto mais estável uma estimativa é no longo prazo, mais confiáveis ​​são as conclusões que podemos tirar dela.

Aqui está um exemplo simples em Python para ilustrar a estabilidade no longo prazo. Suponha que estamos lançando um dado equilibrado e queremos estimar a probabilidade de obter o número 6. Vamos realizar um grande número de lançamentos e verificar como a estimativa da probabilidade se aproxima do valor verdadeiro à medida que aumentamos o número de lançamentos.

import random

def estimar_probabilidade(numero_desejado, num_lancamentos):
    ocorrencias = 0
    for _ in range(num_lancamentos):
        resultado = random.randint(1, 6)
        if resultado == numero_desejado:
            ocorrencias += 1
    probabilidade = ocorrencias / num_lancamentos
    return probabilidade

# Configurações do experimento
numero_desejado = 6
num_lancamentos = 10000

# Estimativa inicial da probabilidade
probabilidade_estimada = estimar_probabilidade(numero_desejado, num_lancamentos)
print(f"Estimativa inicial da probabilidade: {probabilidade_estimada:.4f}")

# Aumentar o número de lançamentos
num_lancamentos *= 10
probabilidade_estimada = estimar_probabilidade(numero_desejado, num_lancamentos)
print(f"Estimativa após {num_lancamentos} lançamentos: {probabilidade_estimada:.4f}")

# Aumentar o número de lançamentos novamente
num_lancamentos *= 10
probabilidade_estimada = estimar_probabilidade(numero_desejado, num_lancamentos)
print(f"Estimativa após {num_lancamentos} lançamentos: {probabilidade_estimada:.4f}")

# Aumentar o número de lançamentos novamente
num_lancamentos *= 10
probabilidade_estimada = estimar_probabilidade(numero_desejado, num_lancamentos)
print(f"Estimativa após {num_lancamentos} lançamentos: {probabilidade_estimada:.4f}")

Estimativa inicial da probabilidade: 0.1653
Estimativa após 100000 lançamentos: 0.1658
Estimativa após 1000000 lançamentos: 0.1663
Estimativa após 10000000 lançamentos: 0.1668

Neste exemplo, definimos uma função estimar_probabilidade que recebe o número desejado (6) e o número de lançamentos e retorna uma estimativa da probabilidade de obter esse número com base nos resultados dos lançamentos. A função utiliza a função random.randint para simular os lançamentos do dado. À medida que aumentamos o número de lançamentos, a função é chamada repetidamente para atualizar a estimativa da probabilidade.

Executando o código, podemos observar como a estimativa da probabilidade se aproxima do valor verdadeiro (1/6) à medida que aumentamos o número de lançamentos. Conforme o número de lançamentos aumenta, a estimativa se torna mais estável e converge para o valor verdadeiro. Isso demonstra o conceito de estabilidade no longo prazo na probabilidade e estatística.

1.2.3.6.4 - Probabilidade como proporção

Probabilidade como proporção é um conceito fundamental na teoria das probabilidades que define a probabilidade de um evento como a proporção de vezes em que esse evento ocorre em relação ao número total de possíveis ocorrências. Vamos detalhar esse conceito e fornecer um exemplo de código Python para ilustrar a ideia de probabilidade como proporção.

A interpretação da probabilidade como proporção é uma abordagem comum na teoria das probabilidades. Segundo essa interpretação, a probabilidade de um evento ocorrer é definida como a proporção de vezes em que esse evento ocorre em relação ao número total de possíveis ocorrências.

Em outras palavras, se temos um conjunto de eventos possíveis e realizamos um grande número de experimentos ou observações, a probabilidade de um evento específico ocorrer é dada pela razão entre o número de vezes que o evento ocorre e o número total de experimentos realizados.

Essa interpretação intuitiva é frequentemente usada em situações do mundo real. Por exemplo, considere o lançamento de um dado justo de seis faces. Se queremos calcular a probabilidade de obter o número 3, podemos realizar um grande número de lançamentos do dado e contar quantas vezes o número 3 aparece. A probabilidade de obter o número 3 será a razão entre o número de vezes que o número 3 ocorreu e o número total de lançamentos.

Aqui está um exemplo simples em Python para ilustrar o conceito de probabilidade como proporção. Vamos simular o lançamento de um dado justo e calcular a probabilidade de obter o número 3.

import random

def calcular_probabilidade(evento, num_lancamentos):
    ocorrencias = 0
    for _ in range(num_lancamentos):
        resultado = random.randint(1, 6)
        if resultado == evento:
            ocorrencias += 1
    probabilidade = ocorrencias / num_lancamentos
    return probabilidade

# Configurações do experimento
evento = 3
num_lancamentos = 10000

# Calcular a probabilidade
probabilidade = calcular_probabilidade(evento, num_lancamentos)
print(f"A probabilidade de obter o número {evento} é: {probabilidade:.4f}")

A probabilidade de obter o número 3 é: 0.1742

Neste exemplo, temos a função calcular_probabilidade que recebe o número do evento (3) e o número de lançamentos e retorna a probabilidade de obter esse número com base nos resultados dos lançamentos. Utilizamos a função random.randint para simular o lançamento do dado e contamos o número de vezes que o evento ocorre.

Ao executar o código, podemos observar a probabilidade estimada de obter o número 3 com base nos lançamentos simulados. Quanto maior o número de lançamentos, mais precisamente a probabilidade estimada se aproximará do valor verdadeiro (1/6, no caso de um dado justo). Isso demonstra o conceito de probabilidade como uma proporção das ocorrências do evento em relação ao número total de experimentos.

1.2.3.6.5 - Limitações na interpretação frequentista

Limitações na interpretação frequentista refere-se a algumas das críticas e limitações associadas à interpretação frequentista da probabilidade. Vamos detalhar essas limitações e comentar sobre código Python para ilustrar algumas delas.

A interpretação frequentista da probabilidade tem sido amplamente utilizada e é baseada na ideia de que a probabilidade de um evento é igual à frequência relativa desse evento em um grande número de experimentos repetidos. No entanto, essa interpretação tem algumas limitações e críticas associadas a ela. Algumas das principais limitações incluem:

• Dependência do número de experimentos: a interpretação frequentista requer um número grande de experimentos para obter resultados confiáveis. Isso pode ser impraticável ou impossível em muitos cenários, especialmente quando lidamos com eventos raros ou experimentos de longo prazo.
• Eventos não repetíveis: existem muitos eventos na vida real que não podem ser repetidos em experimentos múltiplos, como eventos históricos ou eventos únicos e não replicáveis. A interpretação frequentista pode não ser aplicável nesses casos.
• Falta de subjetividade: a interpretação frequentista não leva em consideração as crenças individuais ou a subjetividade associada a um evento. Ela se baseia apenas em frequências observadas, não considerando informações adicionais ou conhecimentos prévios.
• Tratamento de eventos individuais: a interpretação frequentista lida principalmente com a probabilidade de um evento em um conjunto de eventos, mas pode ter dificuldade em lidar com eventos individuais ou sequências específicas de eventos.

Essas são algumas das limitações na interpretação frequentista da probabilidade. Outras interpretações, como a interpretação subjetiva ou a interpretação axiomática, foram desenvolvidas para lidar com essas limitações e fornecer uma abordagem mais flexível e abrangente para a teoria das probabilidades.

Embora as limitações mencionadas não sejam diretamente abordadas por meio de código Python, é possível criar exemplos que demonstrem algumas das limitações práticas da interpretação frequentista. Por exemplo, considere a tentativa de calcular a probabilidade de um evento raro, como a ocorrência de um terremoto de magnitude específica em uma determinada região. A interpretação frequentista exigiria um número muito grande de observações ou um longo período de tempo para obter uma estimativa confiável da probabilidade desse evento raro.

No entanto, a falta de repetibilidade e a dependência de uma grande quantidade de dados podem dificultar a aplicação prática da interpretação frequentista em situações reais. Isso ilustra uma das limitações práticas associadas à interpretação frequentista da probabilidade.

É importante lembrar que a interpretação frequentista é apenas uma das abordagens para a probabilidade e que outras interpretações, como a interpretação subjetiva e a interpretação axiomática, podem ser usadas para contornar algumas dessas limitações e fornecer uma perspectiva mais ampla e flexível sobre a teoria das probabilidades.

1.2.3.7 - Interpretação Axiomática ou Clássica

Na interpretação axiomática ou clássica da probabilidade, a probabilidade é definida com base em um conjunto de axiomas ou regras matemáticas. Vamos detalhar essa interpretação:

• Espaço amostral: a interpretação axiomática parte do conceito de espaço amostral, que é o conjunto de todos os possíveis resultados de um experimento aleatório. Cada resultado individual é chamado de ponto amostral.
• Eventos: Os eventos são subconjuntos do espaço amostral, que representam coleções de pontos amostrais. Um evento pode ser a ocorrência ou não ocorrência de um ou mais resultados.
• Probabilidade como função: Na interpretação axiomática, a probabilidade é definida como uma função matemática que atribui um valor numérico a cada evento. Essa função obedece a certos axiomas ou regras matemáticas que devem ser satisfeitas.
• Axiomas de probabilidade: Existem três axiomas principais que regem a probabilidade na interpretação axiomática:
• a) Axioma da não-negatividade: a probabilidade de um evento é sempre não negativa, ou seja, P(E) ≥ 0 para qualquer evento E.
• b) Axioma da certeza: a probabilidade do espaço amostral completo é igual a 1, ou seja, P(S) = 1, onde S é o espaço amostral.
• c) Axioma da aditividade: se os eventos E1, E2, ..., En são mutuamente exclusivos (não podem ocorrer simultaneamente), então a probabilidade da união desses eventos é igual à soma das probabilidades individuais, ou seja, $P(E1 ∪ E2 ∪ ... ∪ En)$ = $P(E1) + P(E2) + ... + P(En)$.
• Propriedades da probabilidade: além dos axiomas, a probabilidade segue algumas propriedades matemáticas, como a probabilidade de um evento impossível ser igual a 0, a probabilidade complementar ser igual a 1 menos a probabilidade do evento e a probabilidade de dois eventos independentes ocorrerem ser o produto de suas probabilidades individuais.
• Uso em cálculos e previsões: a interpretação axiomática permite que a probabilidade seja tratada de maneira formal e matemática, o que a torna útil para cálculos, previsões e tomada de decisões. Ela fornece uma estrutura sólida para lidar com incerteza e avaliar a probabilidade de eventos em um contexto rigoroso.

Em resumo, a interpretação axiomática ou clássica da probabilidade define a probabilidade como uma função matemática que segue os axiomas de não-negatividade, certeza e aditividade. Essa interpretação fornece uma abordagem formal e rigorosa para a probabilidade, permitindo cálculos precisos e análises estatísticas.

1.2.3.8 - Interpretação Subjetiva

Na interpretação subjetiva da probabilidade, a probabilidade é vista como uma medida subjetiva de incerteza baseada nas crenças e conhecimentos individuais. Vamos detalhar essa interpretação:

Incerteza subjetiva: Na interpretação subjetiva, a probabilidade não está associada a frequências observadas ou propriedades físicas do mundo, mas sim às crenças e opiniões do indivíduo. Cada pessoa pode ter uma interpretação diferente da probabilidade para um evento, com base em sua experiência, conhecimento e avaliação subjetiva.

• Graus de crença: na interpretação subjetiva, a probabilidade é vista como um grau de crença na ocorrência de um evento. Esses graus de crença podem variar de 0 a 1, onde 0 indica completa incredulidade na ocorrência do evento e 1 indica crença absoluta na ocorrência do evento.
• Atualização das crenças: na interpretação subjetiva, as crenças sobre a probabilidade podem ser atualizadas à medida que novas informações são adquiridas. Por exemplo, se uma pessoa inicialmente acredita que a probabilidade de chover hoje é de 0,3, mas depois verifica o relatório meteorológico indicando chuva, sua crença pode ser atualizada para uma probabilidade maior.
• Contextualidade: a interpretação subjetiva considera que a probabilidade pode ser influenciada pelo contexto e pelas informações disponíveis. Diferentes indivíduos podem ter diferentes probabilidades subjetivas para o mesmo evento, dependendo de seus conhecimentos, experiências e avaliações pessoais.
• Uso em tomadas de decisão: a interpretação subjetiva da probabilidade é frequentemente usada em situações de tomada de decisão, em que é necessário avaliar a incerteza e atribuir probabilidades subjetivas aos eventos relevantes. Essas probabilidades subjetivas podem ser usadas para calcular as consequências esperadas das diferentes decisões e auxiliar na escolha da melhor opção.

Em resumo, a interpretação subjetiva da probabilidade se baseia nas crenças e opiniões individuais para atribuir graus de crença às ocorrências de eventos, permitindo a expressão da incerteza de forma subjetiva e sua incorporação na tomada de decisão.

1.2.3.8.1 - Graus de Crença

Na interpretação subjetiva da probabilidade, os graus de crença são uma parte fundamental. Nessa interpretação, a probabilidade é vista como uma medida subjetiva da crença de um indivíduo sobre a ocorrência de um evento. Cada pessoa pode ter seus próprios graus de crença, baseados em suas informações, conhecimentos e experiências.

A interpretação subjetiva permite que os indivíduos expressem suas incertezas e crenças pessoais de forma mais flexível. Em vez de depender de frequências observadas ou repetição de experimentos, a probabilidade é uma medida subjetiva de confiança na ocorrência de um evento.

Aqui está um exemplo de código Python que ilustra a ideia dos graus de crença na interpretação subjetiva:

# Importar bibliotecas
import numpy as np

# Definir uma lista de graus de crença
graus_crenca = [0.2, 0.6, 0.8, 0.4, 0.9]

# Função para verificar se um evento ocorre com base no grau de crença
def ocorre_evento(grau_crenca):
    return np.random.random() < grau_crenca

# Simulação de eventos com base nos graus de crença
for grau_crenca in graus_crenca:
    if ocorre_evento(grau_crenca):
        print("Evento ocorre com grau de crença:", grau_crenca)
    else:
        print("Evento não ocorre com grau de crença:", grau_crenca)

Evento ocorre com grau de crença: 0.2
Evento não ocorre com grau de crença: 0.6
Evento ocorre com grau de crença: 0.8
Evento não ocorre com grau de crença: 0.4
Evento ocorre com grau de crença: 0.9

Neste exemplo, temos uma lista de graus de crença representando a confiança em que um evento ocorra. A função ocorre_evento simula a ocorrência do evento com base no grau de crença, gerando um número aleatório entre 0 e 1 e verificando se é menor que o grau de crença. A simulação é realizada para cada grau de crença na lista. Se o evento ocorrer de acordo com o grau de crença, é exibida a mensagem "Evento ocorre com grau de crença: X", onde X é o grau de crença correspondente. Caso contrário, é exibida a mensagem "Evento não ocorre com grau de crença: X". Este exemplo ilustra como os graus de crença podem ser usados na interpretação subjetiva da probabilidade para expressar a confiança pessoal na ocorrência de um evento. Cada grau de crença representa uma medida subjetiva da probabilidade, baseada nas crenças individuais de cada pessoa.

1.2.3.8.2 - Atualização das Crenças

Na interpretação subjetiva da probabilidade, uma das características importantes é a capacidade de atualizar as crenças à medida que novas informações são adquiridas. Essa atualização é feita por meio do Teorema de Bayes, que permite ajustar as probabilidades a partir de novos dados.

Aqui está um exemplo de código Python que ilustra a atualização das crenças na interpretação subjetiva usando o Teorema de Bayes:

# Importar bibliotecas
import numpy as np

# Definir as probabilidades a priori
probabilidade_priori = 0.5

# Definir a verossimilhança
verossimilhanca = 0.7

# Definir a probabilidade a posteriori
probabilidade_posteriori = (verossimilhanca * probabilidade_priori) / ((verossimilhanca * probabilidade_priori) + ((1 - verossimilhanca) * (1 - probabilidade_priori)))

# Imprimir a probabilidade a posteriori
print("Probabilidade a posteriori:", probabilidade_posteriori)

Probabilidade a posteriori: 0.7

Neste exemplo, consideramos um cenário em que temos uma probabilidade a priori de 0.5, representando a crença inicial em um evento. Em seguida, obtemos uma verossimilhança de 0.7, que representa a evidência ou os novos dados adquiridos.

Usando o Teorema de Bayes, atualizamos as crenças e calculamos a probabilidade a posteriori. A fórmula utilizada é:

$p_{pos}$ = $\frac{v.p_{pri}}{(v.p_{pri})+((1-v)(1-p_{pri}))}$

onde $p_{pos}$ representa a probabilidade a posteriori, $v$ representa a verossimilhança e $p_{pri}$ representa a probabilidade a priori.

A probabilidade a posteriori representa a nova crença ou probabilidade após a incorporação das informações adicionais. Ela é calculada com base nas probabilidades a priori e na verossimilhança.

No código acima, a probabilidade a posteriori é calculada e impressa. Esse processo de atualização das crenças pode ser repetido à medida que novas informações são obtidas, permitindo uma adaptação contínua das probabilidades subjetivas com base nas evidências disponíveis.

Vale ressaltar que o exemplo acima é apenas um caso simples para ilustrar o conceito de atualização de crenças na interpretação subjetiva. Em cenários mais complexos, podem ser considerados múltiplos eventos, dados adicionais e uma abordagem iterativa para atualização das crenças.

1.2.3.8.3 - Contextualidade

Na interpretação subjetiva da probabilidade, a contextualidade refere-se à influência do contexto e das informações disponíveis na formação das crenças probabilísticas. A probabilidade subjetiva de um evento pode variar de pessoa para pessoa, dependendo das informações e do contexto específico em que estão inseridas.

É importante ressaltar que a contextualidade é uma característica inerente à interpretação subjetiva e não é facilmente capturada por meio de um código Python direto. Isso ocorre porque a contextualidade envolve o conhecimento e as experiências individuais, bem como a interpretação pessoal dos dados e das informações disponíveis. No entanto, vamos fornecer um exemplo de código Python simples que ilustra como a contextualidade pode ser considerada em um cenário específico. Considere o seguinte exemplo:

# Importar bibliotecas
import numpy as np

# Definir as informações/contexto disponíveis
informacoes = {
    'Evento A': 0.6,
    'Evento B': 0.4,
    'Evento C': 0.3
}

# Calcular a probabilidade subjetiva com base nas informações/contexto
probabilidade_subjetiva = np.random.choice(list(informacoes.values()))

# Imprimir a probabilidade subjetiva
print("Probabilidade subjetiva:", probabilidade_subjetiva)

Probabilidade subjetiva: 0.4

Nesse exemplo, definimos um dicionário chamado informacoes que representa as informações disponíveis ou o contexto específico. Cada evento é associado a uma probabilidade subjetiva.

Usando a biblioteca NumPy, podemos selecionar aleatoriamente uma das probabilidades subjetivas disponíveis no dicionário informacoes usando np.random.choice(). Isso simula a ideia de que a probabilidade subjetiva depende do contexto específico ou das informações disponíveis.

O exemplo acima é apenas uma representação simplificada da contextualidade na interpretação subjetiva. Em situações reais, a contextualidade é influenciada por uma variedade de fatores e pode envolver uma análise mais complexa e detalhada das informações disponíveis.

Portanto, é importante lembrar que a contextualidade na interpretação subjetiva é um conceito mais abstrato e subjetivo, que envolve a consideração cuidadosa de informações, contexto e conhecimento individual. Não é facilmente traduzida em um código Python direto, mas requer uma avaliação mais ampla do contexto e uma interpretação individual dos dados e das informações disponíveis.

1.2.3.8.4 - Uso em tomadas de decisão

A interpretação subjetiva da probabilidade é frequentemente usada em tomadas de decisão para incorporar crenças individuais e informações contextuais. Forneceremos um exemplo de código Python que ilustra como a interpretação subjetiva pode ser aplicada em um cenário de tomada de decisão.

# Importar bibliotecas
import numpy as np

# Definir as probabilidades subjetivas
prob_A = 0.6  # Probabilidade subjetiva do evento A
prob_B = 0.4  # Probabilidade subjetiva do evento B

# Simular uma tomada de decisão
decisao = np.random.choice(['A', 'B'], p=[prob_A, prob_B])

# Imprimir a decisão tomada
print("Decisão tomada:", decisao)

Decisão tomada: B

Nesse exemplo, definimos duas probabilidades subjetivas prob_A e prob_B, que representam as crenças individuais sobre a probabilidade dos eventos A e B, respectivamente. Em seguida, usamos a função np.random.choice() para realizar uma tomada de decisão, onde selecionamos aleatoriamente um evento com base nas probabilidades subjetivas.

Ao especificar o argumento p em np.random.choice(), podemos fornecer as probabilidades de cada evento ocorrer. No nosso exemplo, usamos as probabilidades subjetivas prob_A e prob_B para atribuir pesos a cada evento na tomada de decisão.

A saída do código fornecerá a decisão tomada com base nas probabilidades subjetivas atribuídas a cada evento. Vale ressaltar que esse é apenas um exemplo simples e que em cenários reais de tomada de decisão, a interpretação subjetiva da probabilidade pode envolver uma análise mais sofisticada das informações disponíveis e a ponderação de várias fontes de incerteza.

Portanto, a interpretação subjetiva da probabilidade pode ser aplicada em tomadas de decisão ao permitir que as crenças individuais e as informações contextuais sejam incorporadas na avaliação de diferentes opções e na atribuição de probabilidades a eventos futuros.

1.2.3.9 - Interpretações modernas da probabilidade

As abordagens modernas da probabilidade buscam ir além das interpretações clássicas, frequentistas e subjetivas, introduzindo conceitos e técnicas mais avançadas para lidar com a incerteza. Destacaremos duas abordagens modernas: a Teoria das Possibilidades e a Teoria das Probabilidades Fuzzy.

• Teoria das Possibilidades: lida com situações em que a incerteza não pode ser quantificada de forma precisa. Em vez de atribuir probabilidades numéricas a eventos, a Teoria das Possibilidades trabalha com graus de possibilidade, representando a medida de quão possível um evento é de ocorrer. Ela é especialmente útil quando há falta de informações ou quando as informações disponíveis são vagas ou imprecisas. A Teoria das Possibilidades permite modelar a incerteza de uma maneira mais flexível e capturar a imprecisão nas estimativas.
• Teoria das Probabilidades Fuzzy: extensão da Teoria das Probabilidades clássica, que lida com a incerteza em termos de graus de pertinência. Ela permite que um evento possua uma probabilidade que varia de 0 a 1, refletindo a medida em que o evento é considerado verdadeiro ou pertinente. Ao contrário da probabilidade clássica, em que um evento é considerado verdadeiro ou falso, a Teoria das Probabilidades Fuzzy permite representar a incerteza de forma mais granular, capturando a ambiguidade e a imprecisão nas informações disponíveis.

Essas abordagens modernas expandem o escopo da teoria clássica da probabilidade, permitindo lidar com incertezas de diferentes naturezas e fornecendo ferramentas para modelar situações complexas. Elas encontram aplicação em áreas como inteligência artificial, sistemas de suporte à decisão, controle de qualidade, entre outras, em que a incerteza desempenha um papel fundamental. É importante ressaltar que as abordagens modernas da probabilidade não substituem as interpretações clássicas, frequentistas e subjetivas, mas sim complementam-nas, oferecendo maneiras alternativas de lidar com a incerteza e a variabilidade nos dados e nas informações disponíveis.

1.2.3.10 - Regras

A teoria das probabilidades é um campo fundamental da matemática e estatística que estuda a incerteza e a aleatoriedade em eventos. Através da teoria das probabilidades, podemos quantificar as chances de um evento ocorrer e analisar como essas chances se relacionam uns com os outros.

As regras da probabilidade são princípios e relações matemáticas que nos ajudam a calcular e manipular probabilidades de forma consistente. Elas são baseadas em axiomas e princípios fundamentais da teoria das probabilidades e fornecem diretrizes claras para realizar cálculos probabilísticos corretos.

As principais regras da probabilidade são:

• Regra da adição: usada para calcular a probabilidade da união de dois eventos mutuamente exclusivos, estabelecendo que a probabilidade de pelo menos um dos eventos ocorrer é igual à soma das probabilidades individuais de cada evento. Sejam A e B dois eventos mutuamente exclusivos, então a probabilidade de pelo menos um deles ocorrer é dada por $P(A ∪ B) = P(A) P(B)$.
• Regra da multiplicação: usada para calcular a probabilidade da interseção de dois eventos independentes, afirmando que a probabilidade de ambos os eventos ocorrerem é o produto das probabilidades individuais de cada evento. Sejam A e B dois eventos independentes, então a probabilidade de ambos ocorrerem é dada por $P(A ∩ B) = P(A) P(B)$.
• Regra da complementaridade: estabelece que a probabilidade de um evento ocorrer somada à probabilidade de seu complemento ocorrer é igual a 1, significando que a probabilidade total de ocorrer um evento ou seu complemento é certa. Matematicamente, $P(A) + P(A') = 1$, onde $A'$ representa o complemento de $A$.

Além dessas regras básicas, também existem outras regras importantes, como a regra da probabilidade condicional, a regra da probabilidade total e a regra de Bayes. Essas regras fornecem ferramentas poderosas para calcular probabilidades condicionais, combinar probabilidades de eventos independentes ou dependentes e atualizar probabilidades com base em informações adicionais.

• Regra da probabilidade condicional: probabilidade de um evento A ocorrer dado que outro evento B já ocorreu. A regra da probabilidade condicional é expressa por P(A|B) = P(A ∩ B) / P(B), onde P(A|B) é a probabilidade condicional de A dado B.
• Regra da probabilidade total: usada quando um evento pode ocorrer de várias maneiras, cada uma com uma probabilidade associada. A probabilidade total de um evento A é dada pela soma das probabilidades de A ocorrer em cada uma dessas maneiras. Matematicamente, P(A) = ∑[P(A|B) * P(B)], onde a soma é realizada para todos os eventos mutuamente exclusivos B que cobrem todo o espaço amostral.
• Regra de Bayes: permite atualizar probabilidades com base em informações adicionais. É usada para calcular a probabilidade de um evento A ocorrer dado que outro evento B já ocorreu. A fórmula da regra de Bayes é P(A|B) = [P(B|A) * P(A)] / P(B), onde P(A|B) é a probabilidade condicional de A dado B.

Essas seis regras são fundamentais na teoria das probabilidades e são amplamente utilizadas em diversos contextos para calcular e relacionar probabilidades de eventos. Elas fornecem as ferramentas necessárias para analisar e quantificar incertezas e são fundamentais para tomadas de decisão informadas em áreas como estatística, ciências naturais, economia e engenharia, entre outras.

O conhecimento e a compreensão dessas regras são essenciais para realizar cálculos precisos de probabilidades, fazer inferências estatísticas corretas e tomar decisões informadas em diversas áreas, como ciências, negócios, engenharia, medicina, entre outras.

Em resumo, as regras da probabilidade são os pilares da análise probabilística e nos permitem quantificar e manipular incertezas de eventos. Elas fornecem um conjunto consistente de princípios matemáticos para lidar com probabilidades e são fundamentais para uma ampla gama de aplicações em diferentes áreas do conhecimento.

1.2.3.10.1 - Regra da adição

A regra da adição é um princípio fundamental na teoria da probabilidade que descreve como calcular a probabilidade da união de dois eventos. Ela nos permite determinar a probabilidade de que pelo menos um dos eventos ocorra.

A regra da adição é aplicável quando os eventos em questão são mutuamente exclusivos, o que significa que não podem ocorrer simultaneamente. Nesse caso, a probabilidade da união de dois eventos é dada pela soma das probabilidades individuais dos eventos, menos a probabilidade da interseção (se houver).

A fórmula geral para a regra da adição é:

$P(A_{ou}B)$ = $P(A)$ + $P(B)$ - $P(A_eB)$

Aqui estão alguns conceitos-chave relacionados à regra da adição:

• Eventos $A$ e $B$: São os eventos cuja probabilidade de união queremos calcular.
• $P(A)$: Representa a probabilidade do evento A ocorrer.
• $P(B)$: Representa a probabilidade do evento B ocorrer.
• $P(A e B)$: Representa a probabilidade da interseção dos eventos A e B, ou seja, a probabilidade de ambos os eventos ocorrerem simultaneamente.

É importante notar que, na regra da adição, subtraímos a probabilidade da interseção dos eventos para evitar a contagem dupla. Se não subtrairmos a probabilidade da interseção, estaremos contando a probabilidade de ambos os eventos ocorrerem duas vezes.

A regra da adição é amplamente utilizada na teoria da probabilidade para calcular a probabilidade de eventos combinados ou eventos que não podem ocorrer simultaneamente.

Exemplo de Código Python:

Vamos considerar um exemplo simples para calcular a probabilidade da união de dois eventos: lançamento de um dado e obter um número par (A) ou obter um número ímpar (B).

# Importar a biblioteca random
import random

# Definir os eventos A e B
evento_A = [2, 4, 6]  # Números pares
evento_B = [1, 3, 5]  # Números ímpares

# Simular o lançamento de um dado
resultado = random.randint(1, 6)

# Verificar se o resultado pertence ao evento A ou B
if resultado in evento_A or resultado in evento_B:
    # Calcular a probabilidade da união P(A ou B)
    prob_uniao = len(evento_A) / 6 + len(evento_B) / 6 - len(evento_A and evento_B) / 6
else:
    prob_uniao = 0.0

# Imprimir o resultado
print("A probabilidade da união dos eventos A ou B é:", prob_uniao)

A probabilidade da união dos eventos A ou B é: 0.5

Nesse exemplo, simulamos o lançamento de um dado e verificamos se o resultado pertence ao evento A (números pares) ou ao evento B (números ímpares). Em seguida, calculamos a probabilidade da união dos eventos A ou B usando a regra da adição.

1.2.3.10.2 - Regra da multiplicação

A regra da multiplicação é um princípio fundamental na teoria da probabilidade que descreve como calcular a probabilidade da ocorrência conjunta de dois eventos independentes. Ela nos permite determinar a probabilidade de que ambos os eventos ocorram simultaneamente.

A regra da multiplicação é aplicável quando os eventos em questão são independentes, ou seja, a ocorrência de um evento não afeta a probabilidade do outro evento ocorrer. Nesse caso, a probabilidade da ocorrência conjunta de dois eventos independentes é dada pelo produto das probabilidades individuais dos eventos.

A fórmula geral para a regra da multiplicação é:

$P(A e B) = P(A) P(B)$

Aqui estão alguns conceitos-chave relacionados à regra da multiplicação:

• Evento $A$ e $B$: são os eventos cuja probabilidade conjunta queremos calcular.
• $P(A)$: representa a probabilidade do evento A ocorrer.
• $P(B)$: representa a probabilidade do evento B ocorrer.
• $P(A e B)$: representa a probabilidade da ocorrência conjunta dos eventos A e B, ou seja, a probabilidade de ambos os eventos ocorrerem simultaneamente.

É importante destacar que a regra da multiplicação é válida apenas para eventos independentes. Se os eventos não forem independentes, a probabilidade da ocorrência conjunta será diferente.

A regra da multiplicação é amplamente utilizada na teoria da probabilidade para calcular a probabilidade de eventos independentes ocorrerem simultaneamente.

Vamos considerar um exemplo simples para calcular a probabilidade da ocorrência conjunta de dois eventos independentes: lançamento de uma moeda e obter cara (A) e lançamento de um dado e obter um número par (B).

# Importar a biblioteca random
import random

# Definir as probabilidades dos eventos A e B
prob_A = 0.5  # Probabilidade de obter cara
prob_B = 0.5  # Probabilidade de obter um número par

# Simular o lançamento da moeda e do dado
resultado_moeda = random.choice(["cara", "coroa"])
resultado_dado = random.choice([1, 2, 3, 4, 5, 6])

# Verificar se os resultados satisfazem os eventos A e B
if resultado_moeda == "cara" and resultado_dado % 2 == 0:
    # Calcular a probabilidade da ocorrência conjunta P(A e B)
    prob_conjunta = prob_A * prob_B
else:
    prob_conjunta = 0.0

# Imprimir o resultado
print("A probabilidade da ocorrência conjunta dos eventos A e B é:", prob_conjunta)

A probabilidade da ocorrência conjunta dos eventos A e B é: 0.0

Nesse exemplo, simulamos o lançamento de uma moeda e de um dado e verificamos se os resultados satisfazem o evento A (obter cara) e o evento B (obter um número par). Em seguida, calculamos a probabilidade da ocorrência conjunta dos eventos A e B usando a regra da multiplicação.

1.2.3.10.3 - Regra da complementaridade

A regra da complementaridade é um conceito fundamental da teoria das probabilidades. Ela estabelece uma relação entre a probabilidade de um evento ocorrer e a probabilidade de seu complemento ocorrer.

O complemento de um evento A, denotado por A', é o evento que consiste em todos os resultados possíveis que não pertencem a A. Em outras palavras, é o conjunto de todos os resultados do espaço amostral que não estão em A.

A regra da complementaridade afirma que a probabilidade de um evento ocorrer somada à probabilidade de seu complemento ocorrer é igual a 1.

Matematicamente, podemos expressar essa regra da seguinte forma: $P(A) + P(A') = 1$, onde $P(A)$ é a probabilidade do evento A ocorrer, e $P(A')$ é a probabilidade do complemento de A ocorrer.

Essa relação decorre do fato de que um evento e seu complemento abrangem todos os resultados possíveis do espaço amostral. Portanto, a probabilidade de um deles ocorrer deve ser igual a 1, que representa a certeza absoluta.

A regra da complementaridade é especialmente útil quando é mais fácil calcular a probabilidade do complemento de um evento do que a probabilidade do próprio evento. Em alguns casos, é mais conveniente calcular a probabilidade do evento contrário ou complementar e, em seguida, usar a regra da complementaridade para determinar a probabilidade do evento original.

Essa regra é amplamente aplicada em diversos contextos, desde a teoria das probabilidades básica até aplicações mais avançadas em estatística e teoria da informação. Ela é essencial para entender a relação entre eventos e para calcular probabilidades de forma consistente.

1.2.3.10.4 - Regra da probabilidade condicional

A probabilidade condicional é a probabilidade de um evento A ocorrer dado que outro evento B já ocorreu.

Essa regra é expressa como:

$P(A|B) = P(A ∩ B) / P(B)$

Onde:

$P(A|B)$ é a probabilidade condicional de A dado B.

$P(A ∩ B)$ é a probabilidade da interseção de A e B.

$P(B)$ é a probabilidade de B ocorrer.

1.2.3.10.5 - Regra da probabilidade total

Essa regra é usada quando um evento pode ocorrer de várias maneiras, sendo que cada uma dessas maneiras tem uma probabilidade associada. A probabilidade total de um evento A é dada pela soma das probabilidades de A ocorrer em cada uma dessas maneiras.

Matematicamente, é expressa como:

$P(A) = ∑[P(A|B) . P(B)]$

Onde:

$P(A)$: a probabilidade de A ocorrer.

$P(B)$: a probabilidade de B ocorrer.

$P(A|B)$: a probabilidade condicional de A dado B.

A soma é realizada para todos os eventos mutuamente exclusivos B que cobrem todo o espaço amostral.

1.2.3.10.6 - Regra de Bayes

A regra de Bayes permite atualizar probabilidades com base em informações adicionais. Ela é especialmente útil quando se deseja determinar a probabilidade de um evento A ocorrer dado que outro evento B já ocorreu. A fórmula da regra de Bayes é:

$P(A|B)$ = $\frac{P(B|A)P(A)}{P(B)}$

Onde:

$P(A|B)$: a probabilidade condicional de A dado B.

$P(B|A)$: a probabilidade condicional de B dado A.

$P(A)$: a probabilidade de A ocorrer.

$P(B)$: a probabilidade de B ocorrer.

Aprofundaremos nosso entendimento sobre as distribuições estatísticas, um tema central na estatística avançada em que você será capaz de reconhecer diferentes tipos de distribuições, e entender suas características fundamentais, como a forma da curva, os parâmetros relevantes e os momentos.

As distribuições estatísticas descrevem o comportamento de variáveis aleatórias e fornecem informações valiosas sobre a probabilidade de diferentes resultados em um conjunto de dados.

• Distribuições Discretas: são aplicadas a variáveis aleatórias discretas, ou seja, variáveis que assumem apenas um conjunto enumerável de valores.
• Distribuição Binomial: modela eventos binários, como o sucesso ou fracasso em uma série de experimentos independentes. Veremos como calcular a probabilidade de obter um número específico de sucessos em um número fixo de tentativas e como utilizar essa distribuição em situações práticas, como estimar a probabilidade de sucesso em testes de produtos ou em pesquisas de opinião.
• Distribuição de Poisson: amplamente utilizada para modelar a ocorrência de eventos raros em um intervalo de tempo ou espaço fixo. Exploraremos exemplos práticos dessa distribuição, como:
• Cálculo da probabilidade de ocorrer um número específico de eventos em um determinado período de tempo.
• A quantidade de chamadas recebidas em um call center.
• O número de acidentes de trânsito em uma determinada área.
• Distribuições Contínuas: são aplicadas a variáveis aleatórias contínuas, ou seja, variáveis que podem assumir qualquer valor dentro de um intervalo contínuo.
• Distribuição Normal: também conhecida como distribuição de Gauss, é uma das distribuições mais importantes e amplamente utilizadas na estatística. Discutiremos as propriedades fundamentais dessa distribuição, como a:
• Forma da curva em formato de sino
• Simetria em torno da média
• Desvio padrão como medida de dispersão inclusive explorando exemplos como a modelagem de dados de altura, peso ou tempo de reação em experimentos científicos.
• Distribuição exponencial: descreve o tempo entre eventos sucessivos em um processo de Poisson. Essa distribuição é frequentemente aplicada em problemas de tempo de vida ou de espera, como a estimativa do tempo médio de vida de um equipamento eletrônico ou a análise do tempo médio de espera em uma fila de atendimento.

Ao invés de nos atermos apenas às definições formais, buscaremos enfatizar a aplicação prática dessas distribuições em problemas do mundo real.

Você será capaz de reconhecer diferentes tipos de distribuições, entender suas características fundamentais e utilizar essas ferramentas para analisar e interpretar dados.

Compreender as distribuições estatísticas é essencial para o desenvolvimento de modelos estatísticos robustos e para tomar decisões informadas com base na incerteza presente nos dados observados.

• Função de densidade de probabilidade (PDF - Probability Density Function): função matemática que descreve a distribuição de probabilidade de uma variável aleatória contínua, fornecendo a probabilidade de um valor específico ocorrer dentro de um intervalo contínuo. É representada graficamente por uma curva, em que a área sob a curva em um intervalo corresponde à probabilidade de ocorrência nesse intervalo. A integral da função de densidade de probabilidade em um intervalo específico fornece a probabilidade de a variável aleatória assumir valores dentro desse intervalo.
• Função de distribuição acumulada (CDF - Cumulative Density Function): função importante associada a uma variável aleatória, sendo definida como a probabilidade de que a variável aleatória seja menor ou igual a um determinado valor. É contínua e crescente, variando de 0 a 1 à medida que o valor da variável aleatória aumenta, fornecendo uma visão mais abrangente da distribuição de probabilidade e permitindo calcularmos a probabilidade acumulada até um certo valor.
• Momentos de uma distribuição (DM - Distribution Moments): medidas estatísticas utilizadas para descrever as características de uma distribuição de probabilidade, calculando-se medidas como a média, a variância, o desvio padrão e a simetria de uma distribuição. O momento de uma distribuição é uma medida estatística que descreve a forma e a localização da distribuição. O momento de ordem n de uma variável aleatória é calculado a partir dos valores da variável aleatória elevados à potência n, ponderados pela sua probabilidade de ocorrência.

As características de uma distribuição são propriedades importantes que ajudam a entender seu comportamento. Algumas das características comuns de uma distribuição incluem:

• Forma da curva: descreve o padrão de variação dos valores da variável aleatória, como uma curva em formato de sino na distribuição normal.
• Simetria: indica se a distribuição é simétrica em torno de um ponto central, como a distribuição normal.
• Centralidade: é representada pela média ou mediana da distribuição, fornecendo uma medida de tendência central.
• Dispersão: refere-se à variação dos valores em relação à medida central, comumente medida pela variância ou desvio padrão.

Ao compreender e explorar esses conceitos, podemos analisar e interpretar melhor as distribuições estatísticas e aplicá-las em problemas do mundo real.

Essas medidas estatísticas nos permitem resumir e quantificar as características das distribuições, o que é essencial para a análise estatística e a tomada de decisões informadas.

1.2.4.1 - Distribuições discretas

As distribuições discretas são um tipo de distribuição estatística em que a variável aleatória assume apenas valores discretos, geralmente inteiros. Isso significa que a distribuição descreve a probabilidade de ocorrência de valores específicos da variável aleatória.

Existem várias distribuições discretas comumente usadas na análise estatística. Algumas das distribuições discretas mais importantes incluem:

• Distribuição de Bernoulli: A distribuição de Bernoulli modela um único experimento com dois resultados possíveis, geralmente rotulados como sucesso (evento de interesse) e falha. Ela é caracterizada por um parâmetro p, que representa a probabilidade de sucesso. A função de probabilidade de uma distribuição de Bernoulli é dada por: $P(X = x)$ = $p^x(1-p)^{(1-x)}$, onde $x = 0$ ou $x = 1$.
• Distribuição Binomial: A distribuição binomial modela o número de sucessos em uma sequência de experimentos independentes de Bernoulli, cada um com a mesma probabilidade de sucesso p. Ela é caracterizada por dois parâmetros: o número de experimentos n e a probabilidade de sucesso p. A função de probabilidade de uma distribuição binomial é dada por: $P(X = k)$ = $C(n, k)$ $p^k(1-p)^{(n-k)}$, onde $X$ é o número de sucessos, $k$ é um valor entre 0 e n, e $C(n, k)$ é o coeficiente binomial.
• Distribuição de Poisson: A distribuição de Poisson modela a ocorrência de eventos raros em um intervalo de tempo ou espaço fixo. Ela é caracterizada por um parâmetro λ, que representa a taxa média de ocorrência dos eventos. A função de probabilidade de uma distribuição de Poisson é dada por: $P(X = k)$ = $\frac{e^{-λ}λ^k}{k!}$, onde $X$ é o número de ocorrências do evento, $k$ é um valor inteiro não negativo, e $e$ é a base do logaritmo natural.
• Distribuição Geométrica: A distribuição geométrica modela o número de tentativas até o primeiro sucesso em uma sequência de experimentos independentes de Bernoulli, cada um com a mesma probabilidade de sucesso p. Ela é caracterizada por um parâmetro p, que representa a probabilidade de sucesso. A função de probabilidade de uma distribuição geométrica é dada por: $P(X = k) = (1-p)^{(k-1)}.p$, onde $X$ é o número de tentativas até o primeiro sucesso e $k$ é um valor inteiro positivo.

Essas são apenas algumas das distribuições discretas mais comuns. Cada distribuição tem suas próprias características e aplicações específicas. Para calcular probabilidades e realizar análises estatísticas usando distribuições discretas, você pode usar bibliotecas estatísticas como o NumPy ou o SciPy em Python, que fornecem funções para trabalhar com essas distribuições e realizar cálculos relevantes.

1.2.4.2 - Distribuição binomial

A distribuição binomial é um tipo de distribuição discreta que modela o número de sucessos em uma sequência de experimentos independentes, cada um com dois resultados possíveis (geralmente rotulados como sucesso e falha). Essa distribuição é amplamente utilizada para analisar eventos binários, como o lançamento de uma moeda, o sucesso ou falha de um produto, entre outros.

A distribuição binomial é caracterizada por dois parâmetros: o número de experimentos n e a probabilidade de sucesso em cada experimento p. O número de experimentos n define o tamanho da sequência de experimentos independentes, enquanto a probabilidade de sucesso p representa a chance de um único experimento resultar em sucesso.

A função de probabilidade da distribuição binomial é dada por: $P(X = k)$ = $C(n,k)$ $p^k (1-p)^{(n-k)}$, onde $X$ é o número de sucessos, $k$ é um valor entre 0 e n, $C(n,k)$ é o coeficiente binomial, dado por $C(n,k) = \frac{n!}{k!(n-k)!}$, e $p^k(1-p)^{n-k}$ é a probabilidade de exatamente $k$ sucessos em $n$ experimentos.

Além da função de probabilidade, a distribuição binomial também possui outras características importantes, como a média e a variância.

A média da distribuição binomial é dada por: $μ = n p$, onde $n$ é o número de experimentos e $p$ é a probabilidade de sucesso, e a variância é dada por: $σ^2 = n p (1-p)$.

Essas fórmulas fornecem uma estimativa do valor médio esperado e da dispersão dos resultados em uma distribuição binomial.

Para calcular probabilidades, realizar análises estatísticas ou gerar amostras aleatórias seguindo uma distribuição binomial, você pode usar bibliotecas estatísticas em Python, como o NumPy ou o SciPy. Essas bibliotecas oferecem funções específicas para trabalhar com a distribuição binomial, como a função binom.pmf() para calcular a função de probabilidade, a função binom.mean() para obter a média e a função binom.rvs() para gerar amostras aleatórias.

1.2.4.3 - Distribuição de Poisson

A distribuição de Poisson é uma distribuição de probabilidade discreta que modela o número de eventos que ocorrem em um intervalo de tempo ou em uma região espacial fixa, quando esses eventos ocorrem de forma independente e a uma taxa média conhecida.

Essa distribuição é amplamente utilizada em estatística para descrever a ocorrência de eventos raros, como chamadas telefônicas em um call center, acidentes de trânsito em uma determinada área ou falhas em um sistema. Ela foi nomeada em homenagem a Siméon-Denis Poisson, um matemático francês que a introduziu no início do século XIX.

Os principais pontos da distribuição de Poisson são os seguintes:

• Parâmetro lambda (λ): É a taxa média de ocorrência dos eventos em um intervalo fixo. Representa o número médio de eventos que se espera ocorrer em uma unidade de tempo ou espaço. Por exemplo, se você sabe que ocorrem, em média, 5 acidentes de trânsito por dia em uma determinada área, λ seria igual a 5.
• Variável aleatória (X): Representa o número de eventos que ocorrem nesse intervalo de tempo ou espaço. Pode assumir valores inteiros não negativos (0, 1, 2, 3, ...) e segue uma distribuição de Poisson.

A função de probabilidade da distribuição de Poisson é dada por: $P(X = k) = \frac{(e^{-λ} . λ^k)}{k!}$, onde $e$ é a base do logaritmo natural (aproximadamente 2,71828), $λ$ é o parâmetro de taxa média de ocorrência, $k$ é o número de eventos que queremos calcular a probabilidade. Essa fórmula permite calcular a probabilidade de ocorrer exatamente $k$ eventos em um intervalo específico, dado um valor $λ$. Além disso, a distribuição de Poisson também possui algumas propriedades interessantes, como a independência dos intervalos não sobrepostos e a soma de variáveis aleatórias de Poisson com a mesma taxa média resultando em outra variável de Poisson com uma taxa média igual à soma das taxas médias individuais.

A distribuição de Poisson é frequentemente utilizada como uma aproximação para modelos mais complexos quando as condições necessárias para sua aplicação são atendidas. É uma ferramenta valiosa em áreas como a teoria das filas, processos estocásticos e análise de dados discretos.

1.2.4.4 - Distribuições contínuas

As distribuições contínuas são um tipo de distribuição de probabilidade em que as variáveis aleatórias podem assumir valores em um intervalo contínuo, ao contrário das distribuições discretas, onde as variáveis aleatórias assumem valores específicos. Nas distribuições contínuas, a função de probabilidade é descrita pela função de densidade de probabilidade (PDF, do inglês Probability Density Function).

A função de densidade de probabilidade descreve a probabilidade relativa de que a variável aleatória assuma um determinado valor dentro de um intervalo contínuo. A área sob a curva da PDF em um intervalo específico representa a probabilidade de a variável aleatória cair dentro desse intervalo.

Existem várias distribuições contínuas importantes, cada uma com suas características distintas. Vou detalhar algumas das distribuições contínuas mais comuns:

• Distribuição Uniforme: nesta distribuição, todos os valores dentro de um intervalo têm a mesma probabilidade de ocorrência. A PDF é uma função constante dentro do intervalo e zero fora dele.
• Distribuição Normal (ou Gaussiana): a distribuição normal é uma das mais importantes e amplamente utilizadas. É caracterizada por sua forma de sino simétrica em torno de um valor médio. A PDF é descrita pela equação da curva gaussiana, que depende do valor médio (μ) e do desvio padrão (σ). A maioria dos fenômenos naturais segue uma distribuição normal.
• Distribuição Exponencial: é frequentemente usada para modelar o tempo entre eventos em um processo de decaimento. A distribuição exponencial é caracterizada por ter uma taxa de ocorrência constante ao longo do tempo. A PDF é decrescente exponencialmente.
• Distribuição de Weibull: é uma distribuição flexível que pode modelar uma variedade de padrões de falha. É frequentemente usada para analisar a confiabilidade e tempo de vida de produtos e sistemas. A PDF de Weibull pode ter formas variáveis, incluindo exponencial, normal e crescente.
• Distribuição de Cauchy: é uma distribuição com caudas longas e pesadas. É conhecida por não ter média ou variância definidas. A PDF de Cauchy possui um pico no centro, mas suas caudas se estendem indefinidamente.

Essas são apenas algumas das distribuições contínuas mais comuns. Existem muitas outras, como a distribuição log-normal, a distribuição gamma, a distribuição beta, entre outras. Cada distribuição tem propriedades específicas e é útil para modelar diferentes tipos de fenômenos em várias áreas da ciência, estatística e engenharia.

1.2.4.5 - Distribuição normal

A distribuição normal, também conhecida como distribuição gaussiana, é uma das distribuições de probabilidade mais importantes e amplamente utilizadas na estatística e em diversas áreas do conhecimento. Ela descreve muitos fenômenos naturais e aleatórios, além de ser a base para muitas técnicas estatísticas e modelos matemáticos.

Características da distribuição normal:

• Forma de sino simétrica: a distribuição normal tem uma forma de sino simétrica em torno de um valor médio.
• Média e mediana iguais: a média, mediana e moda estão todas localizadas no mesmo ponto, no centro da distribuição.
• Curva contínua: a PDF (Probability Density Function) da distribuição normal é uma curva contínua, sem saltos ou descontinuidades.
• Parâmetros: a distribuição normal é completamente definida por dois parâmetros: a média (μ) e o desvio padrão (σ). A média especifica a localização central da distribuição, enquanto o desvio padrão controla a dispersão dos dados em torno da média.

A função de densidade de probabilidade (PDF) da distribuição normal é dada pela conhecida equação da curva gaussiana: $f(x) = \frac{1}{σ\sqrt{2π}} . e^{\frac{-(x - μ)^2}{2σ^2}}$, onde $f(x)$ é a densidade de probabilidade de obter um valor x na distribuição, $μ$ é a média da distribuição, $σ$ é o desvio padrão da distribuição, $π$ é a constante matemática pi (aproximadamente igual a 3.14159) e $e$ é o número neperiano.

Essa equação permite calcular a probabilidade de que uma variável aleatória siga uma distribuição normal em um determinado ponto x da curva.

A distribuição normal é caracterizada por algumas propriedades úteis, como:

• Simetria: a distribuição é simétrica em torno da média, o que significa que a mesma proporção de valores está à esquerda e à direita da média.
• Regra Empírica: aproximadamente 68% dos dados estão dentro de um desvio padrão da média, 95% estão dentro de dois desvios padrão e 99,7% estão dentro de três desvios padrão.
• Transformações lineares: a soma de várias variáveis aleatórias independentes normalmente distribuídas também segue uma distribuição normal. Além disso, uma combinação linear de variáveis aleatórias normalmente distribuídas também é normal.
• Teorema Central do Limite: a soma de um grande número de variáveis aleatórias independentes, independentemente de suas distribuições originais, tende a seguir uma distribuição normal.

A distribuição normal é amplamente utilizada em análise estatística, inferência, modelagem de dados e em várias áreas da pesquisa científica. Ela desempenha um papel fundamental em testes de hipóteses, intervalos de confiança, regressão linear, análise de dados multivariados, entre outros.

1.2.4.6 - Distribuição exponencial

A distribuição exponencial é uma distribuição contínua de probabilidade que é amplamente utilizada para modelar o tempo entre eventos sucessivos de um processo de Poisson. Ela é frequentemente aplicada em áreas como teoria das filas, análise de confiabilidade, tempo de vida de produtos e sistemas, entre outras.

Principais características da distribuição exponencial:

• Tempo entre eventos: a distribuição exponencial é usada para modelar o tempo entre eventos sucessivos que ocorrem em uma taxa média constante.
• Decaimento exponencial: a função de densidade de probabilidade (PDF) da distribuição exponencial apresenta um decaimento exponencial. Ela é caracterizada por ser positiva e decrescente.
• Parâmetro lambda (λ): a distribuição exponencial é definida por um único parâmetro, λ (lambda), que representa a taxa média de ocorrência dos eventos. O inverso de lambda (1/λ) é o valor esperado do tempo entre eventos.
• Probabilidade constante: ao contrário de outras distribuições, como a distribuição normal, a distribuição exponencial não possui memória. Isso significa que a probabilidade de um evento ocorrer em um determinado intervalo de tempo é a mesma, independentemente de quanto tempo já se passou.

A função de densidade de probabilidade (PDF) da distribuição exponencial é dada por: $f(x) = λ e^{-λ x}$, onde $f(x)$ é a densidade de probabilidade de obter um valor $x$ na distribuição, $λ$ é o parâmetro de taxa média de ocorrência dos eventos e $e$ é o número neperiano.

Essa função fornece a probabilidade de que uma variável aleatória siga uma distribuição exponencial e tenha um valor específico x.

Algumas propriedades importantes da distribuição exponencial são:

• Falta de memória: a distribuição exponencial é caracterizada por não possuir memória. Isso significa que a probabilidade de um evento ocorrer em um determinado intervalo de tempo é a mesma, independentemente de quanto tempo já se passou.
• Tempo médio de vida: o tempo médio entre eventos consecutivos em uma distribuição exponencial é igual a 1/λ. Isso significa que a expectativa de tempo até o próximo evento é o inverso da taxa média de ocorrência dos eventos.
• Soma de variáveis exponenciais: a soma de várias variáveis aleatórias independentes com distribuição exponencial também segue uma distribuição exponencial. A taxa média da soma é a soma das taxas médias das variáveis individuais.

A distribuição exponencial é amplamente utilizada em modelagem e análise de dados quando se lida com eventos raros e aleatórios que ocorrem em uma taxa média constante. Ela fornece uma representação matemática útil para esses cenários e possui várias propriedades convenientes para análise estatística.

1.2.4.7 - Funções, métodos e técnicas de distribuição estatística

Vamos detalhar sobre funções, métodos e técnicas de distribuição estatística que são comumente utilizados na análise e modelagem de dados.

• Funções de distribuição acumulada (CDF): descreve a probabilidade de uma variável aleatória ser menor ou igual a um determinado valor. Ela é denotada como F(x) e é definida para todas as distribuições estatísticas. A partir da CDF, é possível calcular probabilidades, quantis e realizar testes de hipóteses.
• Funções de densidade de probabilidade (PDF): descreve a probabilidade de uma variável aleatória assumir um determinado valor. Ela é usada em distribuições contínuas, como a distribuição normal e a distribuição exponencial, e é denotada como f(x). A área sob a curva da PDF em um intervalo específico representa a probabilidade de a variável aleatória cair dentro desse intervalo.
• Funções de sobrevivência: complementar à CDF, e descreve a probabilidade de uma variável aleatória ser maior do que um determinado valor. Ela é denotada como S(x) e é usada principalmente em análise de confiabilidade e tempo de vida, como na distribuição exponencial.
• Funções de quantil: usadas para determinar os valores correspondentes a um determinado percentil ou probabilidade em uma distribuição estatística. Por exemplo, o quantil de 0,5 (ou mediana) divide a distribuição ao meio, com 50% dos valores abaixo e 50% acima desse ponto.
• Métodos de ajuste de distribuição: são utilizados para encontrar a distribuição estatística que melhor se ajusta a um conjunto de dados observados. Esses métodos permitem determinar os parâmetros ótimos da distribuição que melhor descrevem os dados. Alguns métodos comuns incluem o método dos momentos, o método da máxima verossimilhança e o método dos quantis.
• Testes de aderência: usados para avaliar se uma distribuição estatística específica se ajusta bem aos dados observados. Esses testes comparam as características dos dados observados com as características esperadas da distribuição. Alguns testes comuns são o teste de Kolmogorov-Smirnov, o teste qui-quadrado e o teste de Anderson-Darling.
• Técnicas de amostragem: envolvem a seleção de uma amostra representativa de uma população maior. Diferentes métodos de amostragem, como amostragem aleatória simples, amostragem estratificada, amostragem sistemática, entre outros, são usados para garantir que a amostra seja representativa e que os resultados obtidos possam ser generalizados para a população.

Essas são apenas algumas das principais funções, métodos e técnicas de distribuição estatística. Cada uma delas desempenha um papel importante na análise, descrição e modelagem de dados. A escolha da técnica adequada depende do tipo de dados, do objetivo da análise e do contexto específico da aplicação.

1.2.4.8 - Função de densidade de probabilidade (PDF)

A função de densidade de probabilidade (PDF - Probability Density Function), também conhecida como função de probabilidade, é uma função que descreve a distribuição de probabilidade de uma variável aleatória contínua. Ela é usada para determinar a probabilidade de uma variável aleatória assumir valores em um intervalo específico.

A PDF é denotada por f(x), onde "x" é a variável aleatória, satisfazendo as seguintes propriedades:

• A PDF é sempre não negativa: f(x) >= 0 para todos os valores de x.
• A área total sob a curva da PDF é igual a 1: ∫f(x)dx = 1, onde a integral é tomada em todos os possíveis valores da variável aleatória.
• A PDF fornece informações sobre a forma e a distribuição dos valores possíveis de uma variável aleatória contínua. A partir dessa função, podemos derivar várias estatísticas descritivas, como média, mediana, variância, desvio padrão, entre outras.

É importante observar que a PDF é específica para cada distribuição estatística. Diferentes distribuições têm formas de PDF distintas, como a distribuição normal, a distribuição exponencial, a distribuição de Poisson, entre outras. Cada uma dessas distribuições tem uma PDF própria que descreve a forma como os valores estão distribuídos ao longo do eixo x.

A PDF é uma ferramenta essencial na análise estatística, permitindo modelar e compreender as distribuições de variáveis aleatórias contínuas. Ela é utilizada em uma ampla gama de aplicações, desde a inferência estatística até a modelagem de fenômenos complexos em diversas áreas, como ciências naturais, economia, engenharia, entre outras.

Em termos de código Python, é possível utilizar bibliotecas como o SciPy e o matplotlib para plotar a PDF de diferentes distribuições estatísticas. Por exemplo, para plotar a PDF de uma distribuição normal, podemos usar o seguinte código:

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# Parâmetros da distribuição normal
mu = 0  # média
sigma = 1  # desvio padrão

# Valores de x para plotagem da função de densidade de probabilidade
x = np.linspace(-5, 5, 100)

# Calcula a PDF da distribuição normal
pdf = norm.pdf(x, mu, sigma)

# Plota a PDF
plt.plot(x, pdf)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Função de Densidade de Probabilidade (Distribuição Normal)')
plt.grid(True)
plt.show()

Nesse exemplo, utilizamos a biblioteca SciPy para calcular a PDF da distribuição normal (norm.pdf) e a biblioteca matplotlib para plotar o gráfico da função. É possível adaptar o código para outras distribuições estatísticas, alterando os parâmetros e a função correspondente da biblioteca SciPy.

1.2.4.9 - Função de distribuição acumulada

A função de distribuição acumulada (FDA), também conhecida como função de distribuição cumulativa, é uma função que descreve a probabilidade acumulada de uma variável aleatória assumir um valor menor ou igual a um determinado ponto.

A função de distribuição acumulada é denotada por F(x) e é definida para todos os valores de x. Para uma variável aleatória contínua, a função de distribuição acumulada é definida como a integral da função de densidade de probabilidade (PDF) até o valor x: $F(x) = ∫f(t)dt$, para $-∞ < x < ∞$

A função de distribuição acumulada tem as seguintes propriedades:

• A função de distribuição acumulada é não decrescente: $F(x_1) ≤ F(x_2)$ se $x_1 ≤ x_2$.
• A função de distribuição acumulada é limitada: $0 ≤ F(x) ≤ 1$ para todos os valores de $x$.
• A função de distribuição acumulada converge para 0 quando $x$ tende ao menos infinito: $F(x)_{lim(x→∞)} = 0$.
• A função de distribuição acumulada converge para 1 quando x tende ao mais infinito: $F(x)_{lim(x→∞)} = 1$.

A função de distribuição acumulada fornece informações sobre a probabilidade acumulada de observar valores menores ou iguais a um determinado ponto na distribuição. Por exemplo, se F(x) = 0,25, isso significa que há uma probabilidade de 25% de observar valores menores ou iguais a x.

A partir da função de distribuição acumulada, podemos calcular diversas medidas estatísticas, como a mediana m (ponto em que F(x) = 0,5), o percentil p (ponto em que F(x) = p/100) e o quartil q (ponto em que F(x) = q/4).

Em Python, é possível utilizar bibliotecas como o SciPy e o matplotlib para calcular e plotar a função de distribuição acumulada de diferentes distribuições estatísticas. Por exemplo, para plotar a função de distribuição acumulada de uma distribuição normal, podemos usar o seguinte código:

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# Parâmetros da distribuição normal
mu = 0  # média
sigma = 1  # desvio padrão

# Valores de x para plotagem da função de distribuição acumulada
x = np.linspace(-5, 5, 100)

# Calcula a função de distribuição acumulada da distribuição normal
cdf = norm.cdf(x, mu, sigma)

# Plota a função de distribuição acumulada
plt.plot(x, cdf)
plt.xlabel('x')
plt.ylabel('F(x)')
plt.title('Função de Distribuição Acumulada (Distribuição Normal)')
plt.grid(True)
plt.show()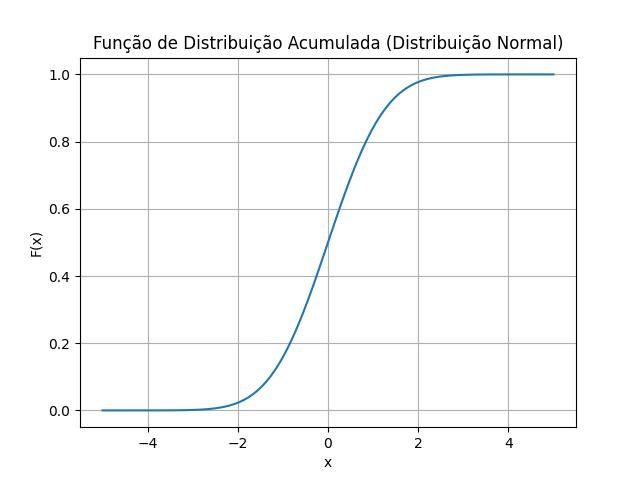

Nesse exemplo, utilizamos a biblioteca SciPy para calcular a função de distribuição acumulada da distribuição normal (norm.cdf) e a biblioteca matplotlib para plotar o gráfico da função. É possível adaptar o código para outras distribuições estatísticas, alterando os parâmetros e a função correspondente da biblioteca SciPy.

1.2.4.10 - Momentos de uma distribuição

Os momentos de uma distribuição são medidas estatísticas que fornecem informações sobre as características e forma da distribuição. Eles são calculados a partir dos valores da variável aleatória e podem ajudar a descrever propriedades como a tendência central, dispersão, assimetria e curtose da distribuição.

Existem diferentes tipos de momentos que podem ser calculados para uma distribuição. Os principais momentos são:

• Primeiro Momento: O primeiro momento de uma distribuição é a média, que representa a tendência central da distribuição. É calculado como a soma dos valores da variável aleatória dividida pelo número total de observações.
• Segundo Momento: O segundo momento de uma distribuição é a variância, que mede a dispersão dos valores em relação à média. A variância é calculada como a média dos quadrados das diferenças entre cada valor e a média.
• Terceiro Momento: O terceiro momento de uma distribuição é a assimetria, que indica a tendência da distribuição de se desviar de uma distribuição simétrica. A assimetria é calculada como a média dos cubos das diferenças entre cada valor e a média, normalizada pela variância ao cubo.
• Quarto Momento: O quarto momento de uma distribuição é a curtose, que mede o grau de achatamento ou apontamento da distribuição em relação à distribuição normal. A curtose é calculada como a média dos quartos poderes das diferenças entre cada valor e a média, normalizada pela variância elevada à quarta potência.

Os momentos podem ser calculados usando funções específicas em bibliotecas de análise estatística, como o NumPy ou o SciPy, em Python. Por exemplo, para calcular a média e a variância de uma lista de valores usando o NumPy, podemos usar o seguinte código:

import numpy as np

# Lista de valores
valores = [2, 4, 6, 8, 10]

# Cálculo da média
media = np.mean(valores)

# Cálculo da variância
variancia = np.var(valores)

print("Média:", media)
print("Variância:", variancia)

Média: 6.0
Variância: 8.0

Para calcular a assimetria e a curtose, o NumPy também possui funções específicas, skew() e kurtosis(), respectivamente:

import numpy as np
from scipy.stats import skew
from scipy.stats import kurtosis

# Lista de valores
valores = [2, 4, 6, 8, 10]

# Cálculo da assimetria
assimetria = skew(valores)

# Cálculo da curtose
curtose = kurtosis(valores)

print("Assimetria:", assimetria)
print("Curtose:", curtose)

Assimetria: 0.0
Curtose: -1.3

Esses são exemplos simples de cálculos de momentos utilizando o NumPy. As bibliotecas de análise estatística oferecem uma ampla variedade de funções para calcular momentos e outras medidas estatísticas, permitindo uma análise mais detalhada das distribuições.

Os conceitos de intervalos de confiança e testes de hipóteses desempenham um papel fundamental na realização de inferências estatísticas.

Um intervalo de confiança é uma faixa de valores estimados que fornece uma estimativa da incerteza associada a uma estimativa pontual de um parâmetro populacional, indicando o intervalo plausível em que o valor verdadeiro do parâmetro pode estar com um certo nível de confiança.

Por exemplo, podemos construir um intervalo de confiança para a média populacional com base em uma amostra aleatória, indicando a faixa de valores em que a média provavelmente está com uma determinada probabilidade de acerto.

Os intervalos de confiança são construídos utilizando a teoria da probabilidade e os conceitos de distribuições amostrais. Geralmente, são baseados em distribuições conhecidas, como a distribuição normal, quando a amostra é grande, ou a distribuição t de Student, quando a amostra é pequena. A construção de um intervalo de confiança envolve a seleção adequada do nível de confiança desejado (geralmente expresso como uma porcentagem, como 95% ou 99%). Os limites inferiores e superiores do intervalo são calculados com base nos dados da amostra e a interpretação correta do intervalo resultante.

Por sua vez, os testes de hipóteses são procedimentos estatísticos utilizados para tomada de decisões sobre uma afirmação ou hipótese a respeito de um parâmetro populacional com base em dados amostrais. O objetivo de um teste de hipóteses é avaliar se existe evidência estatística suficiente para rejeitar ou não uma hipótese nula, que é uma afirmação sobre o valor do parâmetro populacional. O teste de hipóteses envolve a formulação de uma hipótese nula (H0), que assume um valor específico para o parâmetro, e uma hipótese alternativa (H1) que representa a afirmação oposta.

Com base nos dados amostrais e nas suposições estatísticas, calcula-se uma estatística de teste que mede a evidência contrária à hipótese nula. Em seguida, é realizado um cálculo de probabilidade para determinar a probabilidade de obter os resultados observados ou mais extremos, assumindo que a hipótese nula seja verdadeira. Com base na probabilidade calculada, é estabelecido um critério de decisão, chamado de nível de significância (geralmente fixado em 5% ou 1%), que determina se rejeitamos ou não a hipótese nula.

Se a probabilidade de obter os resultados observados ou mais extremos for menor que o nível de significância estabelecido, a hipótese nula é rejeitada, o que sugere que há evidências suficientes para suportar a hipótese alternativa. Caso contrário, não há evidências suficientes para rejeitar a hipótese nula.

Tanto os intervalos de confiança quanto os testes de hipóteses são ferramentas essenciais na inferência estatística, que envolve a generalização dos resultados obtidos em uma amostra para a população maior da qual a amostra foi selecionada.

Essas ferramentas permitem tirar-se conclusões sobre parâmetros populacionais desconhecidos com base em informações limitadas contidas em uma amostra.

Os intervalos de confiança fornecem uma estimativa do intervalo plausível em que o valor verdadeiro do parâmetro populacional está contido, sendo úteis porque reconhecem a incerteza inerente aos dados amostrais e fornecem uma medida de quão precisamente a estimativa amostral reflete o valor verdadeiro do parâmetro.

Além disso, os intervalos de confiança permitem comparar diferentes grupos ou condições e avaliar se há sobreposição nos intervalos, o que pode indicar diferenças significativas entre eles.

Os testes de hipóteses, por sua vez, ajudam a tomar decisões sobre a validade de uma afirmação feita sobre um parâmetro populacional, permitindo-nos avaliar se a evidência amostral é suficientemente forte para rejeitar a hipótese nula em favor da hipótese alternativa.

Os testes de hipóteses são amplamente utilizados em pesquisas científicas, estudos clínicos, análises de dados empresariais e em muitas outras áreas.

Ao utilizar essas ferramentas, é importante compreender seus pressupostos e limitações. Os intervalos de confiança dependem de suposições sobre a distribuição da amostra e exigem amostras aleatórias e representativas. Os testes de hipóteses também estão sujeitos a suposições, como a independência dos dados, normalidade da distribuição e homogeneidade das variâncias. Além disso, é fundamental interpretar corretamente os resultados dos testes de hipóteses, reconhecendo que a rejeição da hipótese nula não implica necessariamente que a hipótese alternativa seja verdadeira, mas sim que há evidências suficientes para questionar a hipótese nula.

Em resumo, os intervalos de confiança e os testes de hipóteses são ferramentas poderosas na inferência estatística, permitindo que os pesquisadores obtenham insights sobre parâmetros populacionais desconhecidos, e tomem decisões baseadas em evidências e avaliem a significância estatística de seus resultados. Essas técnicas ajudam a tornar a estatística uma disciplina robusta e confiável, proporcionando uma base sólida para a tomada de decisões informadas em uma ampla variedade de campos.

1.2.5.1 - Estimativa pontual e a estimativa por intervalo

A estimativa pontual e a estimativa por intervalo são dois métodos utilizados na estatística para estimar um parâmetro desconhecido de uma população com base em uma amostra de dados.

Ambas as abordagens têm o objetivo de fornecer uma estimativa do valor verdadeiro do parâmetro, mas diferem na forma como essa estimativa é apresentada.

A estimativa pontual envolve o cálculo de um único valor numérico que representa a melhor estimativa possível do parâmetro populacional.

Por exemplo, a média amostral é frequentemente usada como uma estimativa pontual da média populacional.

Outros exemplos de estimativas pontuais incluem a proporção amostral, a mediana amostral ou um coeficiente de regressão.

Por outro lado, a estimativa por intervalo fornece uma faixa de valores plausíveis para o parâmetro populacional.

Essa faixa de valores é conhecida como intervalo de confiança e indica a incerteza associada à estimativa.

O intervalo de confiança é construído de tal forma que, com uma determinada probabilidade (geralmente expressa como um nível de confiança, como 95% ou 99%), o intervalo contém o valor verdadeiro do parâmetro.

Em outras palavras, se repetíssemos o processo de amostragem várias vezes, esperaríamos que o intervalo capturasse o valor verdadeiro do parâmetro na maioria das vezes.

A construção de um intervalo de confiança envolve várias etapas, sendo as principais:

• Seleção da amostra: deve-se obter uma amostra representativa da população de interesse, selecionada de forma aleatória ou por algum método de amostragem adequado.
• Escolha do nível de confiança: o nível de confiança determina a probabilidade de que o intervalo de confiança capture o valor verdadeiro do parâmetro. Um nível de confiança comum é 95%, o que significa que, em média, 95% dos intervalos de confiança construídos dessa maneira conteriam o valor verdadeiro do parâmetro.
• Seleção da distribuição apropriada: a escolha da distribuição depende do tamanho da amostra e das características dos dados. Para amostras grandes, a distribuição normal é frequentemente usada. Para amostras pequenas, a distribuição t de Student pode ser mais apropriada.
• Cálculo do estimador pontual: é necessário calcular a estimativa pontual do parâmetro com base na amostra. Isso pode envolver o cálculo da média, proporção, mediana, ou outro estimador adequado, dependendo do parâmetro em questão.
• Cálculo dos limites do intervalo de confiança: os limites do intervalo de confiança são calculados usando fórmulas específicas para a distribuição escolhida. Geralmente, os limites são baseados no estimador pontual, no desvio padrão amostral e no tamanho da amostra.
• Interpretação do intervalo de confiança: o intervalo de confiança resultante é interpretado como uma faixa de valores plausíveis para o parâmetro populacional. Isso significa que, com o nível de confiança escolhido, podemos ter razoável confiança de que o valor verdadeiro do parâmetro está contido dentro do intervalo.

No entanto, não podemos afirmar com certeza absoluta que o valor verdadeiro está dentro do intervalo específico construído a partir da amostra em questão. É importante ressaltar que um intervalo de confiança não indica a probabilidade de que o valor verdadeiro do parâmetro esteja em um intervalo específico fora do intervalo de confiança calculado.

O intervalo de confiança é uma medida da precisão da estimativa e da incerteza associada a ela, não uma medida da probabilidade de que o valor verdadeiro esteja em qualquer ponto específico dentro ou fora do intervalo. Além disso, vale ressaltar que um intervalo de confiança pode variar de amostra para amostra.

Se diferentes amostras forem coletadas da mesma população e os intervalos de confiança forem calculados para cada amostra, é esperado que os intervalos variem. No entanto, em média, os intervalos de confiança construídos a partir de várias amostras capturarão o valor verdadeiro do parâmetro com a taxa de confiança especificada.

Os intervalos de confiança são amplamente utilizados em pesquisas científicas, estudos de mercado, análise de dados empresariais e muitas outras áreas da estatística, fornecendo uma maneira de comunicar a incerteza nas estimativas e permitem que os pesquisadores tomem decisões informadas com base nos dados amostrais disponíveis.

Em resumo, os intervalos de confiança são uma ferramenta estatística importante para estimar parâmetros populacionais desconhecidos, fornecendo uma estimativa pontual acompanhada de uma faixa de valores plausíveis, permitindo que os pesquisadores quantifiquem a incerteza associada à estimativa. Ao entender as etapas para construir um intervalo de confiança e interpretar corretamente seus resultados, é possível tomar decisões mais fundamentadas e confiáveis com base nos dados disponíveis.

Os testes de hipóteses são procedimentos estatísticos utilizados para tomar decisões sobre a validade de uma afirmação feita sobre um parâmetro populacional. Essas afirmações são formuladas em termos de hipótese nula (H0) e hipótese alternativa (H1), também conhecida como hipótese de pesquisa.

A hipótese nula é a afirmação inicial que assume que não há efeito ou diferença significativa entre as amostras ou populações em estudo. Geralmente, é representada pela igualdade, como H0: µ = 0, onde µ é o parâmetro em questão.

A hipótese alternativa, por sua vez, representa a afirmação de que há um efeito ou diferença significativa. Pode ser formulada de três maneiras diferentes:

• H1: µ ≠ 0 (hipótese alternativa bilateral)
• H1: µ > 0 (hipótese alternativa unilateral à direita)
• H1: µ < 0 (hipótese alternativa unilateral à esquerda).

A escolha do nível de significância (geralmente denotado por $α$) é uma etapa crítica no teste de hipóteses, representando a probabilidade de rejeitar a hipótese nula quando ela é realmente verdadeira. É uma medida da tolerância ao erro que estamos dispostos a assumir ao tomar uma decisão.

O valor 0,05 é comum para o nível de significância, correspondendo a uma probabilidade de 5% de rejeitar a hipótese nula quando ela é verdadeira.

Ao realizar um teste de hipóteses, é calculado um valor de teste com base nos dados amostrais e nas suposições feitas sobre a distribuição.

Esse valor de teste é comparado a um valor crítico ou intervalo crítico para tomar a decisão sobre a hipótese nula.

Se o valor de teste estiver fora do intervalo crítico ou menor que o valor crítico, a hipótese nula é rejeitada em favor da hipótese alternativa. Caso contrário, não há evidências suficientes para rejeitar a hipótese nula.

A interpretação dos resultados do teste de hipóteses depende do contexto e das hipóteses formuladas. Se a hipótese nula for rejeitada, isso indica que há evidências estatísticas para suportar a hipótese alternativa. No entanto, isso não significa necessariamente que a hipótese alternativa seja verdadeira, apenas que há evidências para questionar a hipótese nula.

Por outro lado, se a hipótese nula não for rejeitada, isso indica que não há evidências suficientes para suportar a hipótese alternativa. Isso não implica que a hipótese nula seja verdadeira, apenas que não temos evidências convincentes para rejeitá-la. É importante ressaltar que a interpretação dos resultados do teste de hipóteses deve ser feita em conjunto com outras considerações, como a relevância prática, a consistência com a teoria subjacente e a replicação dos resultados em estudos adicionais.

A formulação de hipóteses nulas e alternativas, a escolha do nível de significância e a interpretação dos resultados são etapas fundamentais na realização de testes de hipóteses. Ao formular as hipóteses, é importante ter clareza sobre a afirmação a ser testada e estabelecer tanto a hipótese nula quanto a alternativa de maneira precisa. A escolha do nível de significância determina o grau de confiança desejado na decisão tomada, considerando a possibilidade de erro tipo I (rejeitar erroneamente a hipótese nula) e tipo II (falhar em rejeitar a hipótese nula quando deveria ser rejeitada).

A interpretação dos resultados envolve a avaliação cuidadosa do valor de teste em relação ao valor crítico ou intervalo crítico.

A rejeição da hipótese nula indica evidências estatísticas a favor da hipótese alternativa, enquanto a não rejeição da hipótese nula sugere a falta de evidências suficientes para suportar a hipótese alternativa.

No entanto, é importante lembrar que a rejeição ou não rejeição da hipótese nula não implica em comprovação ou refutação absoluta da afirmação testada.

A interpretação dos resultados deve considerar outros fatores, como contexto, relevância prática e consistência com a teoria subjacente.

Os testes de hipóteses são amplamente utilizados em pesquisas científicas, estudos clínicos, análise de dados de negócios e outras áreas da estatística para realizar inferências sobre parâmetros populacionais desconhecidos, fornecendo um framework estatístico para tomada de decisões baseadas em evidências amostrais, e ajudando a quantificar a incerteza associada às conclusões tiradas dos dados.

Dominar a formulação de hipóteses, a escolha do nível de significância e a interpretação dos resultados é essencial para a prática da estatística e para a realização de estudos confiáveis. Essas ferramentas estatísticas permitem que os pesquisadores façam afirmações fundamentadas e tomem decisões informadas com base nos dados disponíveis, contribuindo para o avanço do conhecimento e para a solução de problemas nas mais diversas áreas.

Gráficos e visualizações desempenham um papel fundamental na análise exploratória de dados, permitindo identificar padrões, tendências e anomalias de forma visualmente intuitiva.

Dentre as diversas opções disponíveis, alguns dos gráficos mais comumente utilizados incluem histogramas, gráficos de dispersão e boxplots.

• Histogramas: gráficos que representam a distribuição de frequências de uma variável contínua, consistindo em barras adjacentes, onde a altura de cada barra representa a frequência ou a densidade de ocorrência de valores dentro de um intervalo específico, permitindo visualizar a forma da distribuição dos dados, identificar a presença de picos ou assimetrias e observar a concentração dos valores em determinadas regiões. Essas informações são úteis para entender a distribuição dos dados e identificar possíveis padrões ou discrepâncias.
• Gráficos de dispersão: são utilizados para investigar a relação entre duas variáveis contínuas, apresentando os valores de uma variável no eixo horizontal e os valores correspondentes da outra variável no eixo vertical. Cada ponto no gráfico representa uma observação. Os gráficos de dispersão permitem visualizar a presença de padrões ou tendências lineares, bem como a dispersão dos dados em torno da tendência. Também podem ser usados para identificar valores atípicos ou anomalias que se desviem da tendência geral.
• Boxplots: também conhecidos como diagramas de caixa, fornecem uma representação visual compacta das principais estatísticas descritivas de uma variável, incluindo a mediana, os quartis e os valores mínimo e máximo. São úteis para comparar distribuições e identificar diferenças nos valores centrais, bem como a presença de valores extremos. Além disso, boxplots permitem detectar assimetrias e avaliar a variabilidade dos dados de forma intuitiva.

Além desses gráficos, existem diversas outras visualizações disponíveis, como gráficos de barras, gráficos de linha, gráficos de pizza, gráficos de áreas, entre outros.

Cada tipo de gráfico possui suas próprias características e é adequado para diferentes tipos de dados e propósitos analíticos.

A escolha da visualização mais adequada depende da natureza dos dados e das perguntas específicas que se deseja responder.

Em suma, gráficos e visualizações são ferramentas poderosas para explorar dados, identificar padrões, tendências e anomalias, e comunicar informações de forma clara e impactante.

Ao utilizar essas representações visuais, é possível obter insights mais profundos sobre os dados e embasar decisões fundamentadas em evidências.

1.2.7.1 - Tendências, discrepâncias e insights sobre os dados

Os gráficos e visualizações desempenham um papel essencial na identificação de tendências, discrepâncias e insights ocultos nos dados.

Eles capacitam os analistas a explorar plenamente o potencial informativo das análises estatísticas, fornecendo uma representação visual dos padrões subjacentes aos dados.

Ao examinar os gráficos, é possível identificar tendências ao longo do tempo ou em relação a outras variáveis.

Por exemplo, um gráfico de linha pode mostrar uma tendência ascendente ou descendente, indicando um aumento ou diminuição consistente em uma determinada variável ao longo do tempo. Isso permite compreender as mudanças e padrões que ocorrem nos dados. Além das tendências, as visualizações também podem revelar discrepâncias ou desvios significativos dos padrões esperados.

Por exemplo, em um gráfico de dispersão, é possível identificar pontos isolados que se desviam da tendência geral, sugerindo valores atípicos ou anomalias que merecem investigação adicional. Essas discrepâncias podem fornecer insights valiosos sobre padrões incomuns ou eventos excepcionais nos dados. Além disso, as visualizações podem revelar insights ocultos, ou seja, informações que não seriam prontamente perceptíveis ao realizar apenas análises estatísticas.

Por exemplo, um gráfico de barras empilhadas pode mostrar a distribuição de uma variável em diferentes grupos, revelando diferenças significativas entre eles. Essas descobertas podem levar a novas perguntas de pesquisa ou orientar a tomada de decisões informadas. As visualizações também facilitam a comunicação de resultados complexos e informações estatísticas de forma clara e concisa, permitindo a apresentação visual de padrões e relacionamentos, tornando mais fácil para o público entender as conclusões e insights derivados das análises estatísticas.

As visualizações capacitam os analistas a explorar, interpretar e comunicar os dados de maneira eficaz, permitindo a identificação de tendências, discrepâncias e insights ocultos nos dados, fornecendo uma visão mais completa e significativa das informações. Ao combinar análises estatísticas com visualizações apropriadas, é possível extrair o máximo de valor dos dados e tomar decisões mais embasadas e informadas.

1.2.7.2 - Tipos de gráficos

Os gráficos e visualizações desempenham um papel fundamental na análise estatística, pois permitem a exploração, comunicação e interpretação dos dados de maneira visualmente atraente e informativa. Eles ajudam a identificar padrões, tendências, relações e discrepâncias nos dados, facilitando a compreensão e a tomada de decisões baseadas em evidências. Vou fornecer uma excelente resenha sobre os principais tipos de gráficos e visualizações utilizados na estatística:

• Gráfico de barras: usado para representar a distribuição de uma variável categórica. Cada categoria é representada por uma barra, cuja altura indica a frequência, proporção ou valor associado à categoria.
• Gráfico de colunas: semelhante ao gráfico de barras, mas as barras são dispostas na vertical em vez de horizontalmente.
• Gráfico de setores (ou gráfico de pizza): usado para representar a distribuição de uma variável categórica em forma de pizza. Cada categoria é representada por uma fatia, cuja área ou ângulo é proporcional à frequência, proporção ou valor associado à categoria.
• Histograma: usado para representar a distribuição de uma variável contínua. O eixo horizontal representa os intervalos de valores e o eixo vertical representa a frequência, proporção ou densidade. Os retângulos adjacentes são desenhados para representar a frequência ou proporção dos valores que caem dentro de cada intervalo.
• Gráfico de dispersão: usado para visualizar a relação entre duas variáveis numéricas. Cada ponto no gráfico representa uma observação com seus valores correspondentes nas duas variáveis. possível identificar padrões, tendências, correlações e outliers através do padrão geral dos pontos.
• Gráfico de linhas: usado para representar a tendência ou mudança ao longo do tempo ou de uma variável em relação a outra. Os pontos são conectados por linhas, mostrando a evolução da variável ao longo de uma sequência temporal ou uma variável independente.
• Gráfico de caixas (boxplot): usado para representar a distribuição de uma variável numérica em termos de seus quartis, mediana, valores mínimos e máximos e possíveis outliers. Ele fornece informações sobre a dispersão, assimetria e presença de valores extremos nos dados.
• Gráfico de área: usado para representar a distribuição ou acumulação de uma variável ao longo do tempo ou de uma sequência. A área abaixo da linha representa a quantidade acumulada ou a proporção da variável.
• Gráfico de dispersão com bolhas: uma variação do gráfico de dispersão onde cada ponto é representado por uma bolha com tamanho proporcional a um terceiro valor associado à observação. Isso permite representar três variáveis simultaneamente.
• Mapas e gráficos geoespaciais: São usados para representar dados em um contexto geográfico, associando-os a regiões, países ou pontos específicos em um mapa.
• Gráfico de área empilhada: uma variação do gráfico de área em que múltiplas séries de dados são empilhadas uma sobre a outra para mostrar a contribuição relativa de cada categoria ao todo.
• Gráfico de radar: usado para comparar múltiplas variáveis em relação a um conjunto comum de categorias. Os valores são representados como pontos em torno de um eixo central, permitindo a visualização dos padrões e diferenças entre as variáveis.
• Gráfico de Gantt: usado para representar o planejamento e o cronograma de atividades em projetos. As barras horizontais representam as tarefas e suas durações, permitindo visualizar a alocação de tempo e as dependências entre as atividades.
• Gráfico de bolhas: uma variação do gráfico de dispersão onde cada ponto é representado por uma bolha com tamanho e cor proporcional a um terceiro e quarto valor associados à observação. Isso permite representar quatro variáveis simultaneamente.
• Gráfico de Sankey: usado para representar fluxos e proporções entre diferentes categorias. As faixas ou setas largas são usadas para representar a magnitude do fluxo de uma categoria para outra.
• Gráfico de rede (network graph): usado para representar relacionamentos complexos entre elementos. Os nós representam os elementos, e as arestas conectam os nós para mostrar as conexões e interações entre eles.
• Gráfico de cascata (waterfall chart): usado para mostrar a contribuição de diferentes fatores para uma mudança em um valor inicial. Ele mostra como o valor inicial é aumentado ou diminuído por cada fator, permitindo visualizar o impacto cumulativo dos diferentes elementos.
• Gráfico de controle: usado para monitorar e controlar processos ao longo do tempo. Ele exibe limites de controle superiores e inferiores, bem como pontos de dados, permitindo a detecção de variações e desvios significativos do processo.
• Gráfico de densidade: usado para visualizar a distribuição de uma variável contínua como uma curva suave. Ele fornece uma representação mais suave da distribuição em comparação com o histograma.
• Gráfico de heat map: usado para representar a relação entre duas variáveis em uma matriz. As células são coloridas de acordo com o valor da relação, permitindo visualizar padrões e tendências.

Esses são apenas alguns exemplos dos muitos tipos de gráficos e visualizações que podem ser utilizados na análise estatística. A escolha do gráfico adequado depende dos dados em questão, do objetivo da análise e da mensagem que se deseja transmitir. É importante criar gráficos claros, precisos e esteticamente agradáveis, que facilitem a compreensão dos dados e destaquem as principais conclusões. As visualizações eficazes podem fornecer insights valiosos e facilitar a comunicação dos resultados de forma impactante e acessível.

1.2.7.2.1 - Gráfico de barras

O gráfico de barras é uma visualização que permite representar a distribuição de uma variável categórica por meio de barras retangulares. Cada categoria é representada por uma barra, cuja altura indica a frequência, proporção ou valor associado à categoria. É uma das visualizações mais comuns e úteis na estatística e na análise de dados.

Aqui estão os principais elementos de um gráfico de barras:

• Eixo x: eixo horizontal do gráfico, que representa as categorias. Cada categoria é posicionada ao longo desse eixo, geralmente com rótulos ou nomes identificando-as.
• Eixo y: eixo vertical do gráfico, que representa a escala numérica dos valores associados às categorias. Pode representar a frequência, proporção, contagem ou qualquer outra medida que seja relevante para a variável categórica.
• Barras: retângulos verticais que representam cada categoria. A altura da barra é proporcional ao valor associado à categoria. A largura das barras pode ser uniforme ou variar dependendo do design do gráfico.
• Rótulos: usados para identificar as categorias ao longo do eixo x e, possivelmente, para fornecer informações adicionais, como valores numéricos exatos ou porcentagens.
• Título: texto descritivo que resume o conteúdo do gráfico de barras. Geralmente está localizado na parte superior do gráfico.
• Legendas: usadas para descrever o significado das barras ou fornecer informações adicionais sobre as categorias. Por exemplo, se as barras representam diferentes grupos ou subcategorias, as legendas podem indicar a que cada grupo pertence.
• Grade: grade de linhas horizontais e/ou verticais que auxilia na leitura e interpretação das barras. Pode ser útil para alinhar visualmente as barras ou fornecer uma referência adicional para os valores representados.
• Cores: barras podem ser coloridas para distinguir visualmente as categorias ou para enfatizar certas informações. As cores podem ser usadas de forma consistente ou variar para cada categoria.

Os gráficos de barras são amplamente utilizados em diversas áreas, como estatística descritiva, análise exploratória de dados, apresentações de resultados e comparações entre categorias. Eles permitem identificar diferenças, padrões ou tendências nos dados categóricos de forma clara e intuitiva.

É importante ressaltar que a escolha adequada de um gráfico de barras depende do contexto e dos objetivos da análise. Além disso, é essencial fornecer uma legenda adequada e garantir que o gráfico esteja devidamente rotulado e dimensionado para uma interpretação precisa dos dados.

Vamos explicar como criar um gráfico de barras utilizando a biblioteca Matplotlib em Python. Para este exemplo, vamos supor que temos uma lista de categorias e seus respectivos valores. Vamos criar um gráfico de barras para representar essa informação.

Primeiro, você precisará instalar a biblioteca Matplotlib, caso ainda não a tenha instalado. Você pode fazer isso executando o seguinte comando no seu ambiente Python:

pip install matplotlib

Aqui está um exemplo de código para criar um gráfico de barras:

import matplotlib.pyplot as plt

# Dados das categorias e seus valores
categorias = ['Categoria 1', 'Categoria 2', 'Categoria 3', 'Categoria 4']
valores = [20, 35, 30, 15]

# Criar o gráfico de barras
plt.bar(categorias, valores)

# Personalizar o gráfico
plt.title('Gráfico de Barras')
plt.xlabel('Categorias')
plt.ylabel('Valores')

# Exibir o gráfico
plt.show()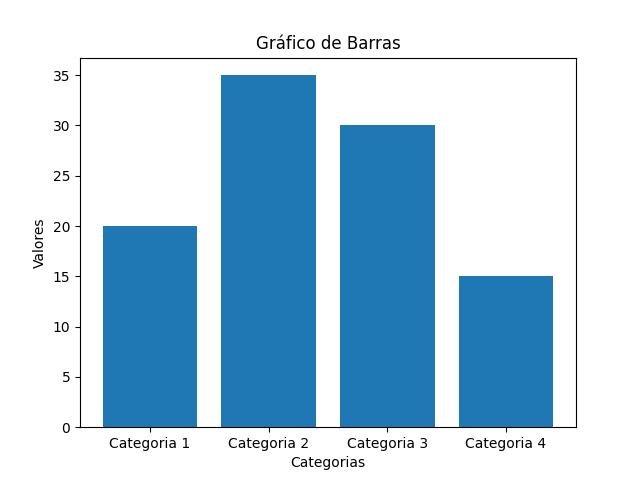

Neste exemplo, importamos o módulo pyplot da biblioteca Matplotlib como plt. Em seguida, definimos as categorias e valores que queremos representar no gráfico de barras.

Utilizamos a função plt.bar() para criar o gráfico de barras, passando as categorias e valores como argumentos. Em seguida, usamos as funções plt.title(), plt.xlabel() e plt.ylabel() para adicionar um título ao gráfico, e rótulos aos eixos x e y, respectivamente.

Por fim, utilizamos plt.show() para exibir o gráfico na tela.

Ao executar o código, você verá o gráfico de barras com as categorias no eixo x e os valores no eixo y. Você também pode personalizar ainda mais o gráfico, adicionando cores, legendas, grade, entre outros elementos, conforme necessário.

1.2.7.2.2 - Gráfico de colunas

O gráfico de colunas, também conhecido como gráfico de barras verticais, é uma visualização que permite representar a distribuição de uma variável categórica por meio de colunas retangulares. Cada categoria é representada por uma coluna, cuja altura indica a frequência, proporção ou valor associado à categoria. O gráfico de colunas é uma variação do gráfico de barras, em que as barras são dispostas verticalmente em vez de horizontalmente.

Aqui estão os principais elementos de um gráfico de colunas:

• Eixo x: eixo horizontal do gráfico, que representa as categorias. Cada categoria é posicionada ao longo desse eixo, geralmente com rótulos ou nomes identificando-as.
• Eixo y: eixo vertical do gráfico, que representa a escala numérica dos valores associados às categorias. Pode representar a frequência, proporção, contagem ou qualquer outra medida que seja relevante para a variável categórica.
• Colunas: retângulos verticais que representam cada categoria. A altura da coluna é proporcional ao valor associado à categoria. A largura das colunas pode ser uniforme ou variar dependendo do design do gráfico.
• Rótulos: usados para identificar as categorias ao longo do eixo x e, possivelmente, para fornecer informações adicionais, como valores numéricos exatos ou porcentagens.
• Título: texto descritivo que resume o conteúdo do gráfico de colunas. Geralmente está localizado na parte superior do gráfico.
• Legendas: usadas para descrever o significado das colunas ou fornecer informações adicionais sobre as categorias. Por exemplo, se as colunas representam diferentes grupos ou subcategorias, as legendas podem indicar a que cada grupo pertence.
• Grade: grade de linhas horizontais e/ou verticais que auxilia na leitura e interpretação das colunas. Pode ser útil para alinhar visualmente as colunas ou fornecer uma referência adicional para os valores representados.
• Cores: As colunas podem ser coloridas para distinguir visualmente as categorias ou para enfatizar certas informações. As cores podem ser usadas de forma consistente ou variar para cada categoria.

O gráfico de colunas é amplamente utilizado para representar e comparar a distribuição de categorias e seus valores associados. Ele é especialmente útil quando há muitas categorias a serem representadas ou quando se deseja destacar visualmente as diferenças entre as categorias.

Assim como no gráfico de barras, é importante garantir que o gráfico de colunas esteja devidamente rotulado, dimensionado e fornecer uma legenda adequada para facilitar a interpretação correta dos dados.

Aqui está um exemplo de código em Python utilizando a biblioteca Matplotlib para criar um gráfico de colunas:

import matplotlib.pyplot as plt

# Dados das categorias e seus valores
categorias = ['Categoria 1', 'Categoria 2', 'Categoria 3', 'Categoria 4']
valores = [20, 35, 30, 15]

# Criar o gráfico de colunas
plt.bar(categorias, valores)

# Personalizar o gráfico
plt.title('Gráfico de Colunas')
plt.xlabel('Categorias')
plt.ylabel('Valores')

# Exibir o gráfico
plt.show()

Neste exemplo, estamos utilizando a biblioteca Matplotlib para criar o gráfico de colunas. A lista categorias contém os rótulos das categorias e a lista valores contém os valores associados a cada categoria.

Utilizamos a função plt.bar() para criar o gráfico de colunas, passando as categorias e valores como argumentos. Em seguida, utilizamos as funções plt.title(), plt.xlabel() e plt.ylabel() para adicionar um título ao gráfico, e rótulos aos eixos x e y, respectivamente.

Por fim, utilizamos plt.show() para exibir o gráfico na tela.

Ao executar o código, você verá o gráfico de colunas com as categorias no eixo x e os valores no eixo y. Você também pode personalizar o gráfico adicionando cores, legendas, grade, entre outros elementos, conforme necessário.

1.2.7.2.3 - Gráfico de setores

O gráfico de setores, também conhecido como gráfico de pizza, é uma visualização que permite representar a distribuição de uma variável categórica por meio de setores de um círculo. Cada categoria é representada por um setor, cujo tamanho angular é proporcional à frequência, proporção ou valor associado à categoria.

Aqui estão os principais elementos de um gráfico de setores:

• Setores: São as fatias circulares que representam cada categoria. O tamanho angular de cada setor é proporcional ao valor associado à categoria. Quanto maior o valor, maior será o ângulo ocupado pelo setor.
• Rótulos: São usados para identificar as categorias dentro de cada setor. Os rótulos são posicionados próximos aos setores correspondentes e geralmente contêm o nome ou descrição da categoria, e possivelmente o valor associado.
• Título: É um texto descritivo que resume o conteúdo do gráfico de setores. Geralmente está localizado na parte central ou superior do gráfico.
• Legenda: É uma tabela ou lista que descreve o significado de cada setor, associando os rótulos das categorias aos valores representados. A legenda é útil para ajudar a identificar e interpretar os setores.
• Cores: Os setores podem ser coloridos para distinguir visualmente as categorias ou para enfatizar certas informações. É comum usar cores diferentes para cada setor, proporcionando uma distinção clara entre as categorias.

O gráfico de setores é comumente utilizado para representar a composição ou a distribuição relativa de diferentes categorias dentro de um todo. Ele é especialmente útil quando se deseja mostrar as proporções de cada categoria em relação ao total.

No entanto, é importante observar que o gráfico de setores pode ter algumas limitações na representação precisa dos dados. A interpretação correta dos setores requer uma boa compreensão dos ângulos e proporções, e é mais adequada quando se trabalha com um pequeno número de categorias distintas.

Aqui está um exemplo de código Python utilizando a biblioteca Matplotlib para criar um gráfico de setores:

import matplotlib.pyplot as plt

# Dados das categorias e seus valores
categorias = ['Categoria 1', 'Categoria 2', 'Categoria 3', 'Categoria 4']
valores = [20, 35, 30, 15]

# Criar o gráfico de setores
plt.pie(valores, labels=categorias)

# Personalizar o gráfico
plt.title('Gráfico de Setores')

# Exibir o gráfico
plt.show()

Neste exemplo, utilizamos a função plt.pie() para criar o gráfico de setores, passando os valores das categorias e os rótulos como argumentos. O gráfico é então personalizado com o título utilizando a função plt.title(), e é exibido na tela usando plt.show().

Ao executar o código, você verá o gráfico de setores com os setores circulares representando cada categoria. Os rótulos das categorias são exibidos ao lado de seus respectivos setores.

Espero que esta explicação detalhada tenha sido útil para entender o conceito do gráfico de setores!

1.2.7.2.4 - Histograma

O histograma é uma visualização gráfica que permite representar a distribuição de uma variável quantitativa contínua ou discreta. Ele divide o intervalo dos valores em várias faixas chamadas de "intervalos" ou "bins" e mostra a frequência ou a densidade de ocorrência dos valores dentro de cada intervalo.

Aqui estão os principais elementos de um histograma:

• Eixo x: É o eixo horizontal do histograma, que representa a escala dos valores da variável em estudo. O eixo x é dividido em intervalos ou bins, e cada intervalo representa uma faixa de valores.
• Eixo y: É o eixo vertical do histograma, que representa a frequência ou densidade de ocorrência dos valores dentro de cada intervalo. A escala do eixo y depende da escolha de representação do histograma: frequência absoluta, frequência relativa, densidade ou outra medida relevante.
• Intervalos (bins): São as faixas em que o eixo x é dividido. Cada intervalo representa uma faixa de valores contínuos ou um conjunto de valores discretos. A largura e o número de intervalos podem variar dependendo da distribuição dos dados e do objetivo do histograma.
• Barras: São retângulos verticais que representam cada intervalo no histograma. A altura da barra é proporcional à frequência ou densidade de ocorrência dos valores dentro do intervalo.
• Rótulos: São usados para identificar os intervalos ao longo do eixo x e, possivelmente, para fornecer informações adicionais, como os limites dos intervalos ou as categorias representadas.
• Título: É um texto descritivo que resume o conteúdo do histograma. Geralmente está localizado na parte superior do gráfico.
• Legendas: São usadas para descrever o significado das barras ou fornecer informações adicionais sobre a distribuição dos valores. As legendas podem incluir informações como média, mediana, desvio padrão, entre outros.

Os histogramas são amplamente utilizados para explorar e visualizar a distribuição de uma variável, identificar padrões, detectar assimetrias, avaliar a concentração ou dispersão dos dados, entre outras análises descritivas.

Aqui está um exemplo de código Python utilizando a biblioteca Matplotlib para criar um histograma:

import matplotlib.pyplot as plt

# Dados da variável
dados = [22, 30, 32, 35, 38, 40, 42, 45, 50, 55, 60, 65, 70, 72, 75]

# Criar o histograma
plt.hist(dados, bins=5)

# Personalizar o histograma
plt.title('Histograma')
plt.xlabel('Valores')
plt.ylabel('Frequência')

# Exibir o histograma
plt.show()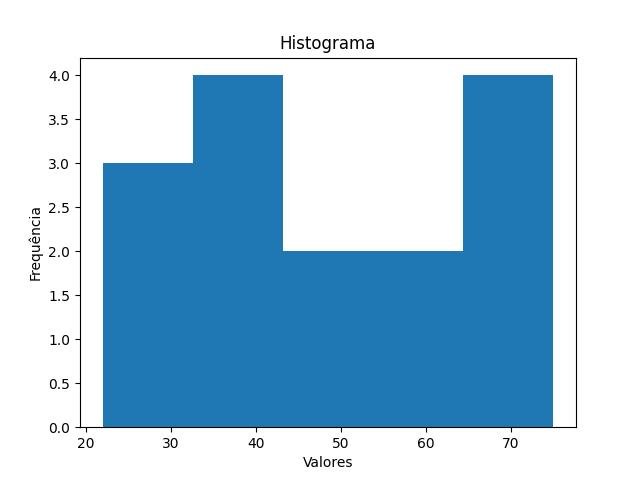

Neste exemplo, utilizamos a função plt.hist() para criar o histograma, passando os dados da variável e o número de bins como argumentos. O histograma é personalizado com um título, rótulos nos eixos x e y, utilizando as funções plt.title(), plt.xlabel() e plt.ylabel(), respectivamente. Por fim, o histograma é exibido na tela com plt.show().

Ao executar o código, você verá o histograma representando a distribuição dos valores

1.2.7.2.5 - Gráfico de dispersão

O gráfico de dispersão, também conhecido como gráfico de pontos, é uma visualização que permite explorar a relação entre duas variáveis quantitativas. Ele representa os pontos de dados em um plano cartesiano, onde cada ponto representa um par de valores correspondentes às duas variáveis.

Aqui estão os principais elementos de um gráfico de dispersão:

• Eixo x: É o eixo horizontal do gráfico, que representa os valores da primeira variável. Essa variável é geralmente referida como variável independente ou variável explanatória.
• Eixo y: É o eixo vertical do gráfico, que representa os valores da segunda variável. Essa variável é geralmente referida como variável dependente ou variável de resposta.
• Pontos: São os marcadores no gráfico que representam cada par de valores correspondentes às duas variáveis. Cada ponto é posicionado no plano cartesiano com base nos valores das duas variáveis.
• Título: É um texto descritivo que resume o conteúdo do gráfico de dispersão. Geralmente está localizado na parte superior do gráfico.
• Rótulos: São usados para identificar as variáveis ao longo dos eixos x e y. Eles fornecem informações sobre o que cada eixo representa e podem incluir unidades de medida, quando aplicável.
• Legendas: São usadas para descrever o significado dos pontos ou fornecer informações adicionais sobre os dados representados no gráfico.
• Linha de tendência: Opcionalmente, pode-se traçar uma linha de tendência ou linha de regressão que represente o padrão geral dos pontos. Essa linha pode ajudar a identificar padrões ou tendências na relação entre as variáveis.

Os gráficos de dispersão são frequentemente utilizados para identificar correlações, padrões, outliers ou qualquer relação entre duas variáveis. Eles permitem visualizar a dispersão dos dados e analisar a relação geral entre as variáveis.

Aqui está um exemplo de código Python utilizando a biblioteca Matplotlib para criar um gráfico de dispersão:

import matplotlib.pyplot as plt

# Dados das variáveis
x = [1, 2, 3, 4, 5, 6]
y = [3, 5, 4, 6, 8, 7]

# Criar o gráfico de dispersão
plt.scatter(x, y)

# Personalizar o gráfico
plt.title('Gráfico de Dispersão')
plt.xlabel('Variável X')
plt.ylabel('Variável Y')

# Exibir o gráfico
plt.show()

Neste exemplo, utilizamos a função plt.scatter() para criar o gráfico de dispersão, passando as duas variáveis x e y como argumentos. O gráfico é então personalizado com um título, rótulos nos eixos x e y, utilizando as funções plt.title(), plt.xlabel() e plt.ylabel(), respectivamente. Por fim, o gráfico de dispersão é exibido na tela com plt.show().

Ao executar o código, você verá o gráfico de dispersão representando a relação entre as variáveis x e y, onde cada ponto corresponde a um par de valores das duas variáveis.

1.2.7.2.6 - Gráfico de linhas

O gráfico de linhas é uma visualização que conecta pontos de dados através de segmentos de linha reta. Ele é usado para representar a evolução ou tendência de uma variável ao longo de um eixo de tempo ou outro tipo de escala contínua. É especialmente útil para mostrar a mudança progressiva de um valor ao longo de um período ou para comparar várias séries temporais.

Aqui estão os principais elementos de um gráfico de linhas:

• Eixo x: É o eixo horizontal do gráfico, que representa a escala de tempo ou outra escala contínua. Geralmente, é utilizado para representar os períodos, datas ou pontos de referência correspondentes aos valores.
• Eixo y: É o eixo vertical do gráfico, que representa os valores da variável em estudo. Pode representar qualquer medida quantitativa ou contínua.
• Linhas: São segmentos de linha reta que conectam os pontos de dados no gráfico. Cada ponto representa um valor específico da variável no eixo y em relação à posição correspondente no eixo x. As linhas permitem observar tendências, mudanças ao longo do tempo e padrões gerais da variável.
• Título: É um texto descritivo que resume o conteúdo do gráfico de linhas. Geralmente está localizado na parte superior do gráfico.
• Rótulos: São usados para identificar as variáveis ao longo dos eixos x e y. Fornecem informações sobre o que cada eixo representa e podem incluir unidades de medida, quando aplicável.
• Legendas: São usadas para descrever o significado de cada linha no gráfico, especialmente quando há várias séries de dados sendo representadas.
• Marcadores: Opcionalmente, é possível adicionar marcadores (pontos) nos pontos de dados para enfatizar sua localização exata no gráfico.

Os gráficos de linhas são amplamente utilizados para visualizar a tendência ao longo do tempo de uma variável, identificar padrões, comparar várias séries de dados ou destacar mudanças significativas. Eles fornecem uma representação clara e intuitiva da evolução dos valores.

Aqui está um exemplo de código Python utilizando a biblioteca Matplotlib para criar um gráfico de linhas:

import matplotlib.pyplot as plt

# Dados das variáveis
x = [1, 2, 3, 4, 5, 6]
y = [3, 5, 4, 6, 8, 7]

# Criar o gráfico de linhas
plt.plot(x, y)

# Personalizar o gráfico
plt.title('Gráfico de Linhas')
plt.xlabel('Eixo X')
plt.ylabel('Eixo Y')

# Exibir o gráfico
plt.show()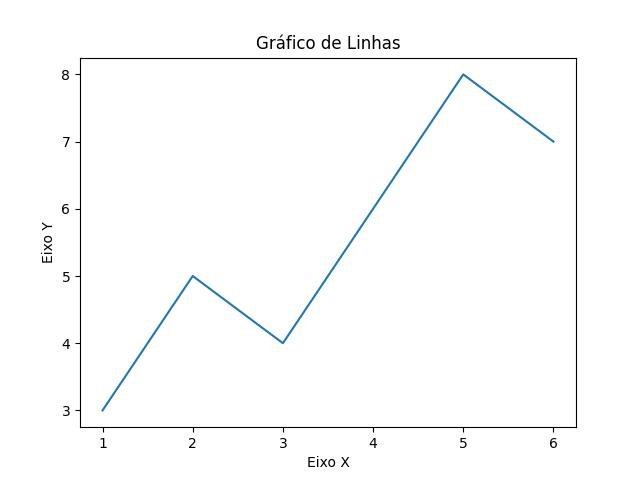

Neste exemplo, utilizamos a função plt.plot() para criar o gráfico de linhas, passando as duas variáveis x e y como argumentos. O gráfico é personalizado com um título, rótulos nos eixos x e y, utilizando as funções plt.title(), plt.xlabel() e plt.ylabel(), respectivamente. Por fim, o gráfico de linhas é exibido na tela com plt.show().

Ao executar o código, você verá o gráfico de linhas representando a relação entre as variáveis x e y, mostrando a tendência ou evolução dos valores ao longo do eixo x.

1.2.7.2.7 - Gráfico de caixas (boxplot)

O gráfico de caixas, também conhecido como boxplot, é uma visualização estatística que fornece informações sobre a distribuição de um conjunto de dados numéricos. Ele é especialmente útil para explorar a dispersão dos dados, identificar valores atípicos (outliers) e comparar distribuições entre diferentes grupos ou categorias.

Aqui estão os principais elementos de um gráfico de caixas (boxplot):

• Caixa (Box): É a parte central do gráfico que representa a distribuição dos dados. Ela é definida pelos quartis (Q1, Q2 e Q3) do conjunto de dados. O Q2 (segundo quartil) corresponde à mediana dos dados. O Q1 (primeiro quartil) é o valor que separa os 25% dos dados mais baixos, enquanto o Q3 (terceiro quartil) separa os 25% dos dados mais altos. A altura da caixa é conhecida como amplitude interquartil (IQR), calculada como IQR = Q3 - Q1.
• Linha mediana (Median): É uma linha dentro da caixa que indica a posição da mediana (Q2).
• Bigodes (Whiskers): São as linhas que se estendem a partir da caixa. Eles representam a extensão dos dados dentro de um intervalo específico. Os bigodes são geralmente calculados com base no IQR, estendendo-se 1,5 vezes o IQR a partir dos quartis Q1 e Q3. Pontos fora dessa extensão são frequentemente considerados valores atípicos.
• Valores atípicos (Outliers): São pontos individuais que estão além dos bigodes. Eles podem ser indicativos de valores extremos ou anômalos no conjunto de dados.
• Título: É um texto descritivo que resume o conteúdo do gráfico de caixas. Geralmente está localizado na parte superior do gráfico.
• Rótulo: É usado para identificar o eixo vertical e pode fornecer informações sobre a variável representada.

Os gráficos de caixas são amplamente utilizados para resumir e comparar a distribuição de dados numéricos em diferentes grupos ou categorias. Eles permitem visualizar a mediana, a dispersão dos dados, a presença de valores atípicos e identificar possíveis diferenças entre os grupos.

Aqui está um exemplo de código Python utilizando a biblioteca Seaborn para criar um gráfico de caixas:

import seaborn as sns

# Dados das variáveis
grupo1 = [10, 12, 15, 18, 20, 22, 25]
grupo2 = [5, 8, 10, 12, 15, 18, 20]

# Criar o gráfico de caixas
sns.boxplot(data=[grupo1, grupo2])

# Personalizar o gráfico
plt.title('Gráfico de Caixas')
plt.ylabel('Valores')

# Exibir o gráfico
plt.show()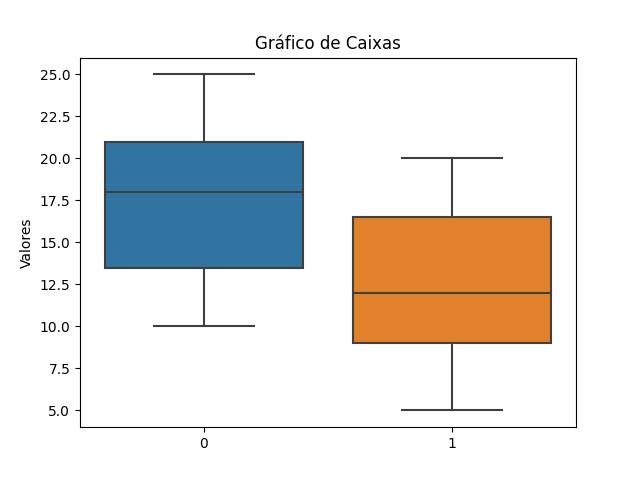

Neste exemplo, utilizamos a função sns.boxplot() do Seaborn para criar o gráfico de caixas, passando os dados dos grupos como uma lista de listas. O gráfico é personalizado com um título e um rótulo no eixo y utilizando as funções plt.title() e plt.ylabel(), respectivamente. Por fim, o gráfico de caixas é exibido na tela com plt.show().

Ao executar o código, você verá o gráfico de caixas representando a distribuição dos valores nos grupos 1 e 2, permitindo a comparação entre eles.

Espero que esta explicação detalhada tenha sido útil para entender o conceito do gráfico de caixas (boxplot)!

1.2.7.2.8 - Gráfico de área

O gráfico de área é uma visualização que mostra a distribuição ou a contribuição de diferentes categorias ao longo de um eixo. É uma variação do gráfico de linha em que a área abaixo da linha é preenchida, criando uma representação visual da contribuição de cada categoria em relação ao todo.

Aqui estão os principais elementos de um gráfico de área:

• Eixo x: É o eixo horizontal do gráfico, que representa as categorias ou o intervalo de valores em que os dados estão agrupados.
• Eixo y: É o eixo vertical do gráfico, que representa a escala numérica ou a proporção da contribuição de cada categoria.
• Áreas: São as regiões preenchidas abaixo das linhas, que representam a contribuição de cada categoria em relação ao todo. Cada categoria é representada por uma área colorida no gráfico.
• Título: É um texto descritivo que resume o conteúdo do gráfico de área. Geralmente está localizado na parte superior do gráfico.
• Rótulos: São usados para identificar as categorias ao longo do eixo x e podem incluir unidades de medida, quando aplicável.
• Legendas: São usadas para descrever o significado de cada área ou fornecer informações adicionais sobre as categorias representadas no gráfico.

Os gráficos de área são comumente usados para visualizar a distribuição de dados ao longo do tempo ou para comparar a contribuição de diferentes categorias em um conjunto de dados. Eles permitem identificar tendências, proporções e mudanças na distribuição ao longo do eixo x.

Aqui está um exemplo de código Python utilizando a biblioteca Matplotlib para criar um gráfico de área:

import matplotlib.pyplot as plt

# Dados das categorias
categorias = ['Categoria A', 'Categoria B', 'Categoria C', 'Categoria D']
valores = [30, 45, 25, 50]

# Criar o gráfico de área
plt.stackplot(categorias, valores, labels=categorias)

# Personalizar o gráfico
plt.title('Gráfico de Área')
plt.xlabel('Categorias')
plt.ylabel('Valores')

# Exibir as legendas
plt.legend(loc='upper left')

# Exibir o gráfico
plt.show()

Neste exemplo, utilizamos a função plt.stackplot() para criar o gráfico de área, passando as categorias e os valores correspondentes como argumentos. Utilizamos a opção labels para fornecer rótulos para as áreas correspondentes às categorias. O gráfico é personalizado com um título, rótulos nos eixos x e y, utilizando as funções plt.title(), plt.xlabel() e plt.ylabel(), respectivamente. Também exibimos as legendas utilizando a função plt.legend() e especificando a localização onde devem ser exibidas. Por fim, o gráfico de área é exibido na tela com plt.show().

Ao executar o código, você verá o gráfico de área representando a contribuição das categorias A, B, C e D, permitindo a comparação visual da contribuição de cada categoria.

Espero que esta explicação detalhada tenha sido útil para entender o conceito do gráfico de área!

1.2.7.2.9 - Gráfico de dispersão com bolhas

O gráfico de dispersão com bolhas, também conhecido como bubble plot, é uma visualização que combina as características do gráfico de dispersão tradicional com o uso de bolhas para representar uma terceira variável. É útil para explorar a relação entre duas variáveis contínuas e adicionar uma dimensão adicional para representar uma variável adicional através do tamanho das bolhas.

Aqui estão os principais elementos de um gráfico de dispersão com bolhas:

• Eixo x: Representa a primeira variável contínua que está sendo analisada.
• Eixo y: Representa a segunda variável contínua que está sendo analisada.
• Bolhas: São representações gráficas dos pontos de dados, onde o tamanho da bolha é proporcional a uma terceira variável. Quanto maior o tamanho da bolha, maior é o valor correspondente da terceira variável.
• Título: É um texto descritivo que resume o conteúdo do gráfico de dispersão com bolhas. Geralmente está localizado na parte superior do gráfico.
• Rótulos: São usados para identificar as variáveis ao longo dos eixos x e y e podem incluir unidades de medida, quando aplicável.
• Legenda: É usada para descrever o significado do tamanho das bolhas, representando a terceira variável. Geralmente é exibida em uma caixa de legenda na parte do gráfico.

Os gráficos de dispersão com bolhas são úteis para identificar padrões, tendências e correlações entre duas variáveis contínuas, além de fornecer uma dimensão adicional através do tamanho das bolhas. Eles são amplamente utilizados para visualizar dados multidimensionais e comunicar informações complexas de forma eficaz.

Aqui está um exemplo de código Python utilizando a biblioteca Matplotlib para criar um gráfico de dispersão com bolhas:

import matplotlib.pyplot as plt
import numpy as np

# Dados das variáveis
x = np.random.rand(50)  # Exemplo de valores aleatórios para o eixo x
y = np.random.rand(50)  # Exemplo de valores aleatórios para o eixo y
z = np.random.rand(50)  # Exemplo de valores aleatórios para a terceira variável

# Criar o gráfico de dispersão com bolhas
plt.scatter(x, y, s=z*1000, alpha=0.5)

# Personalizar o gráfico
plt.title('Gráfico de Dispersão com Bolhas')
plt.xlabel('Eixo X')
plt.ylabel('Eixo Y')

# Exibir o gráfico
plt.show()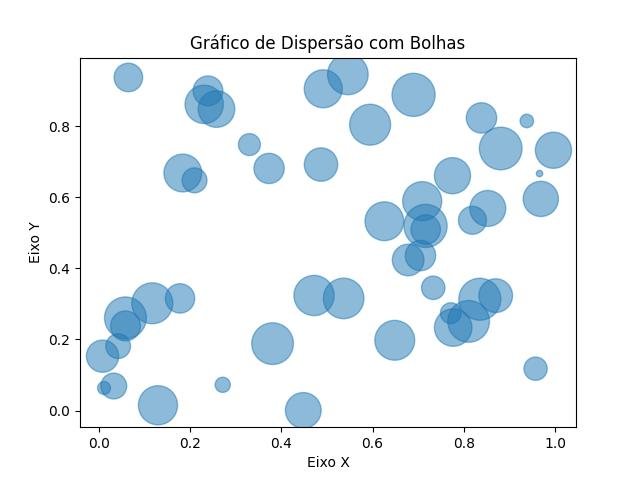

Neste exemplo, utilizamos a função plt.scatter() para criar o gráfico de dispersão com bolhas. Passamos os valores das variáveis x e y como argumentos para os eixos x e y, respectivamente. A variável z é utilizada para determinar o tamanho das bolhas, multiplicando por 1000 (no exemplo) e utilizando o argumento s da função scatter(). O argumento alpha define a transparência das bolhas. O gráfico é personalizado com um título, rótulos nos eixos x e y, utilizando as funções plt.title(), plt.xlabel() e plt.ylabel(), respectivamente. Por fim, o gráfico de dispersão com bolhas é ex

1.2.7.2.10 - Mapas e gráficos geoespaciais

Mapas e gráficos geoespaciais são visualizações que representam dados relacionados a localizações geográficas. Eles são amplamente utilizados para analisar padrões espaciais, identificar tendências regionais e comunicar informações geográficas de forma visualmente eficaz.

Existem várias técnicas e ferramentas para criar mapas e gráficos geoespaciais, e algumas delas são:

• Sistemas de Informação Geográfica (SIG): São ferramentas que permitem a captura, armazenamento, análise e exibição de dados geográficos. Eles fornecem recursos avançados para criar mapas, realizar análises espaciais e integrar dados geográficos com outras informações.
• Shapefiles: São arquivos populares para armazenar dados geoespaciais. Eles consistem em arquivos com extensão .shp que contêm geometrias (pontos, linhas, polígonos) representando características geográficas, como países, cidades, estradas, entre outros. Esses arquivos podem ser lidos e processados por várias bibliotecas de geoprocessamento em diferentes linguagens de programação.
• Bibliotecas de Geoprocessamento: Existem diversas bibliotecas disponíveis para processamento e visualização de dados geoespaciais em diferentes linguagens de programação. Alguns exemplos populares incluem:
• Python: GeoPandas, Shapely, Folium, Basemap.
• R: ggplot2, leaflet, sp.
• JavaScript: Leaflet, D3.js, Mapbox.
• Mapas de calor (Heatmaps): São representações visuais que utilizam cores para mostrar a intensidade ou densidade de um fenômeno geográfico em uma área específica. Eles são úteis para identificar padrões de concentração ou dispersão de dados em um mapa.
• Cartogramas: São mapas que distorcem a forma e o tamanho das áreas geográficas com base em uma variável específica. Eles são usados para enfatizar a representação proporcional de dados em uma área geográfica, como população, renda per capita, entre outros.
• Gráficos de densidade espacial (Spatial Density Plots): São gráficos que representam a densidade de ocorrência de eventos em um mapa. Eles são úteis para identificar áreas de maior ou menor concentração de eventos, como crimes, acidentes, pontos de interesse, entre outros.
• Visualizações 3D: Além dos mapas tradicionais em duas dimensões, também é possível criar visualizações geoespaciais em três dimensões. Isso permite explorar dados em diferentes alturas, inclinações e perspectivas, proporcionando uma experiência imersiva.

Essas são apenas algumas das técnicas e ferramentas disponíveis para criar mapas e gráficos geoespaciais. A escolha da técnica adequada dependerá dos dados e das informações que você deseja visualizar e analisar. É importante considerar a natureza dos dados geográficos, as necessidades de análise espacial e as habilidades e recursos disponíveis.

Aqui está um exemplo de código para criar um mapa simples usando Folium:

import folium

# Criar um objeto de mapa
mapa = folium.Map(location=[-22.9068, -43.1729], zoom_start=12)

# Adicionar um marcador no mapa
folium.Marker([-22.9068, -43.1729], popup='Rio de Janeiro').add_to(mapa)

# Exibir o mapa
mapa.save('mapa.html')

Neste exemplo, importamos a biblioteca folium e criamos um objeto de mapa usando a função folium.Map(). Passamos a localização inicial do mapa (latitude e longitude) e o nível de zoom desejado.

Em seguida, adicionamos um marcador ao mapa usando a função folium.Marker(). Passamos a localização do marcador (latitude e longitude) e um texto de popup que será exibido quando o marcador for clicado.

Por fim, usamos o método save() para salvar o mapa em um arquivo HTML chamado "mapa.html". Você pode abrir esse arquivo em um navegador para visualizar o mapa interativo.

Você pode personalizar ainda mais o mapa adicionando camadas, polígonos, linhas, cores e muito mais. O Folium oferece uma série de recursos e opções de personalização para criar mapas interativos ricos em detalhes.

Lembre-se de instalar a biblioteca Folium usando o pip antes de executar o código:

pip install folium

Espero que este exemplo tenha sido útil! Você pode explorar a documentação oficial do Folium para obter mais informações e exemplos avançados: https://python-visualization.github.io/folium/

1.2.7.2.11 - Gráfico de área empilhada

O gráfico de área empilhada, também conhecido como stacked area chart, é uma visualização que mostra a distribuição de várias categorias ao longo de um eixo, empilhando as áreas correspondentes a cada categoria. Ele é semelhante ao gráfico de área, mas no gráfico de área empilhada, as áreas das categorias são sobrepostas umas sobre as outras, criando uma representação visual das proporções relativas entre as categorias.

Aqui estão os principais elementos de um gráfico de área empilhada:

• Eixo x: É o eixo horizontal do gráfico, que representa as categorias ou o intervalo de valores em que os dados estão agrupados.
• Eixo y: É o eixo vertical do gráfico, que representa a escala numérica ou a proporção da contribuição de cada categoria.
• Áreas empilhadas: São as áreas preenchidas abaixo das linhas, representando as contribuições de cada categoria em relação ao todo. As áreas são empilhadas uma sobre a outra, mostrando a soma cumulativa das proporções das categorias.
• Título: É um texto descritivo que resume o conteúdo do gráfico de área empilhada. Geralmente está localizado na parte superior do gráfico.
• Rótulos: São usados para identificar as categorias ao longo do eixo x e podem incluir unidades de medida, quando aplicável.
• Legendas: São usadas para descrever o significado de cada área empilhada ou fornecer informações adicionais sobre as categorias representadas no gráfico.

Os gráficos de área empilhada são comumente usados para visualizar a distribuição de dados ao longo do tempo ou para comparar as contribuições de diferentes categorias em um conjunto de dados. Eles permitem identificar tendências, proporções e mudanças na distribuição ao longo do eixo x, bem como a contribuição relativa de cada categoria para o todo.

Aqui está um exemplo de código Python utilizando a biblioteca Matplotlib para criar um gráfico de área empilhada:

import matplotlib.pyplot as plt

# Dados das categorias
categorias = ['Categoria A', 'Categoria B', 'Categoria C']
valores1 = [20, 35, 15]  # Valores para a primeira categoria
valores2 = [30, 15, 25]  # Valores para a segunda categoria
valores3 = [10, 30, 20]  # Valores para a terceira categoria

# Criar o gráfico de área empilhada
plt.stackplot(categorias, valores1, valores2, valores3, labels=['Valor 1', 'Valor 2', 'Valor 3'])

# Personalizar o gráfico
plt.title('Gráfico de Área Empilhada')
plt.xlabel('Categorias')
plt.ylabel('Valores')

# Exibir as legendas
plt.legend(loc='upper left')

# Exibir o gráfico
plt.show()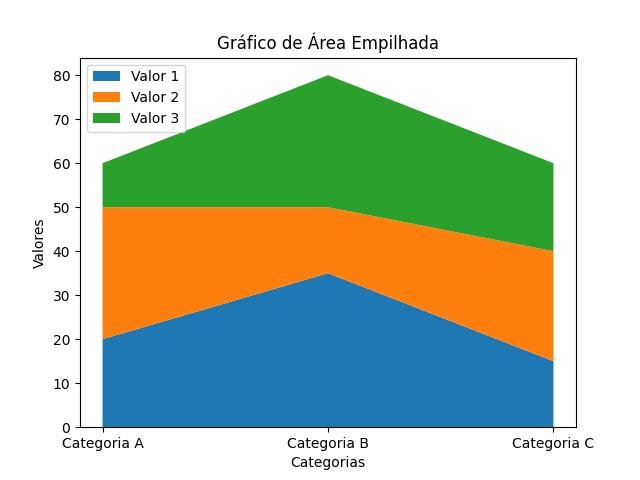

Neste exemplo, utilizamos a função plt.stackplot() para criar o gráfico de área empilhada. Passamos as categorias e os valores correspondentes para cada categoria como argumentos. Utilizamos a opção labels para fornecer rótulos para cada área empilhada. O gráfico é personalizado com um título, rótulos nos eixos x e y, utilizando as funções plt.title(), `plt

1.2.7.2.12 - Gráfico de radar

O gráfico de radar, também conhecido como gráfico de teia ou gráfico de aranha, é uma visualização que representa múltiplas variáveis em um formato radial. É útil para comparar o desempenho ou características de diferentes categorias em relação a várias métricas.

Aqui estão os principais elementos de um gráfico de radar:

• Eixo radial: É composto por várias linhas que partem de um ponto central e se estendem em direções diferentes. Cada linha representa uma variável ou métrica.
• Eixo angular: É uma circunferência ou uma série de ângulos que indicam as diferentes direções das linhas radiais. Cada ângulo representa uma categoria ou uma unidade de observação.
• Linhas de dados: São linhas que conectam os pontos de dados correspondentes a cada categoria nas linhas radiais. Elas representam o valor de cada variável para a categoria correspondente.
• Área fechada: Em alguns casos, as linhas de dados podem ser preenchidas para formar uma área fechada. Isso pode ajudar a enfatizar a distribuição e o padrão geral dos dados.
• Rótulos: São usados para identificar as variáveis ao longo das linhas radiais e as categorias ao longo do eixo angular.
• Legenda: É usada para descrever o significado das linhas ou áreas no gráfico de radar, indicando a qual categoria ou variável cada linha se refere.

Os gráficos de radar são úteis para comparar o desempenho ou características de várias categorias em relação a diferentes variáveis. Eles permitem identificar padrões, pontos fortes e pontos fracos em diferentes métricas para cada categoria. Além disso, o formato radial facilita a comparação entre as categorias, pois todas as variáveis estão representadas na mesma escala e na mesma visualização.

Aqui está um exemplo de código Python utilizando a biblioteca Matplotlib para criar um gráfico de radar:

import numpy as np
import matplotlib.pyplot as plt

# Dados das variáveis e categorias
variaveis = ['Variável A', 'Variável B', 'Variável C', 'Variável D', 'Variável E', 'Variável F']
categorias = ['Categoria 1', 'Categoria 2', 'Categoria 3', 'Categoria 4', 'Categoria 5', 'Categoria 6']

# Valores para cada categoria e variável
valores_categoria1 = [3, 4, 2, 5, 3]
valores_categoria2 = [4, 2, 3, 2, 5]
valores_categoria3 = [2, 5, 4, 3, 2]
valores_categoria4 = [5, 3, 2, 4, 4]
valores_categoria5 = [3, 2, 5, 3, 4]
valores_categoria6 = [4, 2, 2, 3, 3]

# Criar o gráfico de radar
fig, ax = plt.subplots(figsize=(6, 6), subplot_kw={'projection': 'polar'})
ax.set_theta_offset(np.pi/2)
ax.set_theta_direction(-1)

# Calcular os ângulos para cada variável
angulos = np.linspace(0, 2*np.pi, len(variaveis), endpoint=False).tolist()

# Adicionar as linhas de dados para cada categoria
ax.plot(angulos, valores_categoria1 + [valores_categoria1[0]], label='Categoria 1')
ax.plot(angulos, valores_categoria2 + [valores_categoria2[0]], label='Categoria 2')
ax.plot(angulos, valores_categoria3 + [valores_categoria3[0]], label='Categoria 3')
ax.plot(angulos, valores_categoria4 + [valores_categoria4[0]], label='Categoria 4')
ax.plot(angulos, valores_categoria5 + [valores_categoria5[0]], label='Categoria 5')
ax.plot(angulos, valores_categoria6 + [valores_categoria6[0]], label='Categoria 6')

# Personalizar o gráfico
ax.set_xticks(angulos)
ax.set_xticklabels(variaveis)
ax.yaxis.grid(True)
ax.legend()

# Exibir o gráfico
plt.show()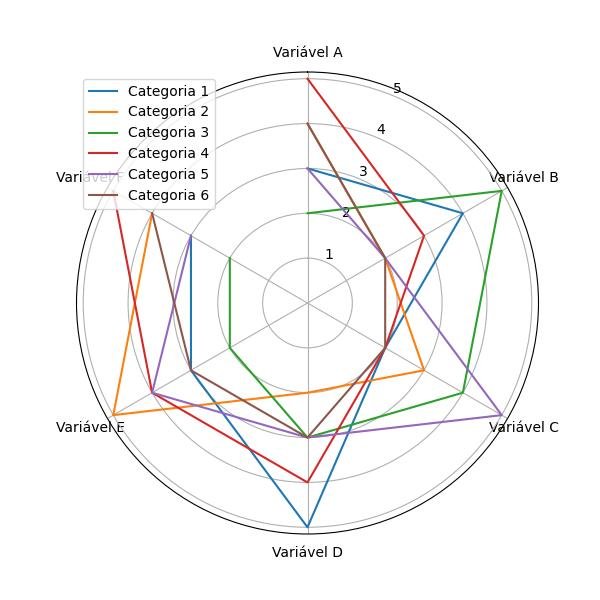

Neste exemplo, utilizamos a função plt.subplots() para criar uma figura e um conjunto de eixos para o gráfico de radar. Configuramos o subplot_kw com {'projection': 'polar'} para criar um gráfico polar.

Em seguida, definimos os ângulos para cada variável utilizando a função np.linspace() e adicionamos as linhas de dados correspondentes a cada categoria usando a função ax.plot(). É importante fechar o polígono, adicionando o primeiro valor novamente ao final de cada lista de valores.

Personalizamos o gráfico definindo os ângulos no eixo x, as etiquetas das variáveis, habilitando as linhas de grade no eixo y e exibindo a legenda.

Finalmente, exibimos o gráfico usando a função plt.show().

Espero que este exemplo tenha sido útil! Você pode explorar mais opções de personalização e funcionalidades da biblioteca Matplotlib para criar gráficos de radar mais avançados.

1.2.7.2.13 - Gráfico de Gantt

O gráfico de Gantt é uma visualização que representa as tarefas de um projeto em um cronograma, mostrando a duração de cada tarefa e a sobreposição entre elas. É uma ferramenta amplamente utilizada na gestão de projetos para planejar, acompanhar e visualizar o progresso das atividades ao longo do tempo.

Aqui estão os principais elementos de um gráfico de Gantt:

• Linhas de tarefas: São as linhas horizontais que representam cada tarefa do projeto. Cada linha é rotulada com o nome da tarefa ou uma identificação única.
• Barras de tarefas: São barras horizontais que representam a duração de cada tarefa. As barras são posicionadas ao longo do eixo de tempo do gráfico.
• Eixo de tempo: É o eixo horizontal do gráfico que representa o período de tempo em que as tarefas são executadas. Pode ser exibido em dias, semanas, meses, etc.
• Rótulos de data: São usados para identificar as datas ao longo do eixo de tempo. Podem ser exibidos em intervalos regulares, como dias ou semanas.
• Dependências entre tarefas: Podem ser representadas por setas ou linhas conectando as barras de tarefas. Isso mostra a sequência de execução das tarefas e as relações de dependência entre elas.
• Legenda: É usada para fornecer informações adicionais sobre as cores, símbolos ou outros elementos do gráfico.

Os gráficos de Gantt são úteis para visualizar a ordem e a duração das tarefas de um projeto, identificar sobreposições ou lacunas na programação, determinar dependências entre as atividades e acompanhar o progresso do projeto ao longo do tempo.

Existem várias bibliotecas em Python que podem ser usadas para criar gráficos de Gantt, como matplotlib, plotly e gantt. Aqui está um exemplo de código usando a biblioteca matplotlib:

import matplotlib.pyplot as plt
import matplotlib.dates as mdates

# Dados das tarefas
tarefas = ['Tarefa A', 'Tarefa B', 'Tarefa C', 'Tarefa D']
datas_inicio = ['2023-01-01', '2023-01-05', '2023-01-10', '2023-01-15']
duracoes = [5, 8, 6, 4]  # Duração em dias

# Converter as datas para o formato apropriado
datas_inicio = [mdates.datestr2num(data) for data in datas_inicio]

# Criar o gráfico de Gantt
fig, ax = plt.subplots()

# Configurar o eixo x como datas
ax.xaxis_date()
ax.xaxis.set_major_formatter(mdates.DateFormatter('%y-%m-%d'))

# Plotar as barras de tarefas
ax.barh(tarefas, duracoes, left=datas_inicio)

# Personalizar o gráfico
ax.set_xlabel('Data')
ax.set_ylabel('Tarefas')
ax.set_title('Gráfico de Gantt')

# Exibir o gráfico
plt.show()

Neste exemplo, importamos as bibliotecas matplotlib.pyplot e matplotlib.dates. Definimos os dados das tarefas, incluindo os nomes das tarefas, as

1.2.7.2.14 - Gráfico de bolhas

O gráfico de bolhas, também conhecido como bubble chart, é uma visualização que representa dados em três dimensões: duas dimensões para os eixos x e y e a terceira dimensão para o tamanho das bolhas. É uma forma eficaz de mostrar a relação entre três variáveis e destacar padrões ou clusters nos dados.

Aqui estão os principais elementos de um gráfico de bolhas:

• Eixo x e eixo y: São os eixos horizontal e vertical que representam duas variáveis independentes. Cada ponto de dados é posicionado de acordo com os valores dessas duas variáveis.
• Tamanho das bolhas: É uma terceira variável que determina o tamanho das bolhas no gráfico. Quanto maior o valor dessa variável, maior será o tamanho da bolha correspondente.
• Rótulos: São usados para identificar os pontos de dados ou fornecer informações adicionais sobre cada bolha.
• Legenda: É usada para descrever o significado das bolhas ou fornecer informações adicionais sobre as variáveis representadas no gráfico.

Os gráficos de bolhas são úteis para mostrar relacionamentos complexos entre três variáveis e identificar padrões, clusters ou anomalias nos dados. Eles são especialmente úteis quando a terceira variável (tamanho das bolhas) é significativa e adiciona uma dimensão adicional à visualização.

Aqui está um exemplo de código Python utilizando a biblioteca Matplotlib para criar um gráfico de bolhas:

import numpy as np
import matplotlib.pyplot as plt

# Dados das variáveis
x = np.random.rand(50)  # Valores para o eixo x
y = np.random.rand(50)  # Valores para o eixo y
tamanhos = np.random.rand(50) * 100  # Valores para o tamanho das bolhas

# Criar o gráfico de bolhas
plt.scatter(x, y, s=tamanhos, alpha=0.5)

# Personalizar o gráfico
plt.title('Gráfico de Bolhas')
plt.xlabel('Eixo X')
plt.ylabel('Eixo Y')

# Exibir o gráfico
plt.show()

Neste exemplo, utilizamos a função plt.scatter() para criar o gráfico de bolhas. Passamos os valores para os eixos x e y como argumentos, e utilizamos a opção s para definir os tamanhos das bolhas com base nos valores da terceira variável. A opção alpha é usada para controlar a transparência das bolhas.

O gráfico é personalizado com um título, rótulos nos eixos x e y, utilizando as funções plt.title(), plt.xlabel() e plt.ylabel().

Você pode personalizar ainda mais o gráfico de bolhas, como alterar as cores das bolhas, adicionar uma legenda, aplicar escala aos tamanhos das bolhas ou adicionar informações adicionais aos rótulos. A biblioteca Matplotlib oferece várias opções de personalização para criar gráficos de bolhas visualmente atraentes e informativos.

1.2.7.2.15 - Gráfico de Sankey

O gráfico de Sankey, também conhecido como diagrama de fluxo de Sankey, é uma visualização que representa o fluxo de dados, recursos ou quantidades entre diferentes categorias. É uma forma eficaz de mostrar relações de entrada e saída, proporções e fluxos entre diferentes elementos de um sistema.

Aqui estão os principais elementos de um gráfico de Sankey:

• Nós: São as categorias ou elementos do sistema representados por retângulos ou caixas. Cada nó é rotulado com o nome ou identificação da categoria.
• Fluxos: São as conexões entre os nós que representam o fluxo de dados, recursos ou quantidades. Os fluxos são representados por setas ou linhas de diferentes espessuras, que indicam a quantidade ou proporção do fluxo.
• Rótulos: São usados para identificar os fluxos ou fornecer informações adicionais sobre cada conexão.
• Proporções: As larguras dos fluxos podem ser usadas para representar as proporções relativas entre os nós e a quantidade de fluxo entre eles.

Os gráficos de Sankey são úteis para visualizar e analisar o fluxo de dados ou recursos em sistemas complexos, como redes de energia, fluxos de tráfego, processos industriais, orçamentos financeiros, entre outros. Eles permitem identificar gargalos, distribuição desigual de recursos e entender como as quantidades são divididas e transferidas entre diferentes categorias.

Existem várias bibliotecas em Python que podem ser usadas para criar gráficos de Sankey, como plotly, matplotlib e networkx. Aqui está um exemplo de código usando a biblioteca plotly:

import plotly.graph_objects as go

# Dados dos nós e fluxos
nos = ["A", "B", "C", "D", "E"]
fluxos = {
    "A": {"B": 20, "C": 30},
    "B": {"D": 15},
    "C": {"D": 10, "E": 20},
    "D": {"E": 5}
}

# Criar as listas de fontes, alvos e valores dos fluxos
sources = []
targets = []
values = []

# Mapear os nomes dos nós para índices
indice_nos = {nome: idx for idx, nome in enumerate(nos)}

# Iterar sobre os dados dos fluxos
for origem, destinos in fluxos.items():
    for destino, valor in destinos.items():
        sources.append(indice_nos[origem])
        targets.append(indice_nos[destino])
        values.append(valor)

# Criar o gráfico de Sankey
fig = go.Figure(data=[go.Sankey(
    node=dict(
        label=nos,
        pad=15,
        thickness=20
    ),
    link=dict(
        source=sources,  # Usar índices dos nós de origem
        target=targets,  # Usar índices dos nós de destino
        value=values
    )
)])

# Personalizar o gráfico
fig.update_layout(title_text="Gráfico de Sankey")

# Exibir o gráfico
fig.show()

Neste exemplo, importamos a biblioteca plotly.graph_objects e definimos os dados dos nós e fluxos. Cada nó é representado por uma string única, e os fluxos são definidos como um dicionário em que as chaves são os nós de origem e os valores são

1.2.7.2.16 - Gráfico de rede (network graph)

O gráfico de rede, também conhecido como network graph ou grafo, é uma visualização que representa as relações entre diferentes elementos em um conjunto de dados. É composto por nós (ou vértices) e arestas (ou conexões) que representam as interações, conexões ou relações entre os nós.

Aqui estão os principais elementos de um gráfico de rede:

• Nós (vértices): São os elementos individuais do conjunto de dados. Cada nó pode representar uma entidade, uma pessoa, um local ou qualquer objeto do conjunto de dados. Os nós são geralmente representados por pontos ou formas.
• Arestas (conexões): São as linhas ou conexões entre os nós que representam as relações ou interações entre eles. As arestas podem ser direcionais (com uma seta que indica a direção da relação) ou não direcionais (sem seta, indicando uma relação bidirecional).
• Peso das arestas: Em alguns casos, as arestas podem ter um peso ou valor associado, que representa a intensidade, a frequência ou a força da relação entre os nós. Isso pode ser visualizado usando a espessura das arestas.
• Rótulos: São usados para identificar os nós ou fornecer informações adicionais sobre cada elemento. Os rótulos podem ser os nomes dos nós ou quaisquer outras informações relevantes.

Os gráficos de rede são úteis para visualizar relações complexas e interconexões em dados que podem não ser facilmente compreendidos em outras formas de visualização. Eles são amplamente utilizados em diversas áreas, como redes sociais, análise de redes, ciência de dados, sistemas complexos, entre outros.

Existem várias bibliotecas em Python que podem ser usadas para criar gráficos de rede, como networkx, igraph e plotly. Aqui está um exemplo de código usando a biblioteca networkx:

import networkx as nx
import matplotlib.pyplot as plt

# Criar um objeto de grafo
G = nx.Graph()

# Adicionar nós ao grafo
G.add_nodes_from([1, 2, 3, 4, 5])

# Adicionar arestas ao grafo
G.add_edges_from([(1, 2), (1, 3), (2, 3), (2, 4), (3, 4), (4, 5)])

# Layout do grafo
pos = nx.spring_layout(G)

# Desenhar os nós
nx.draw_networkx_nodes(G, pos)

# Desenhar as arestas
nx.draw_networkx_edges(G, pos)

# Adicionar rótulos aos nós
nx.draw_networkx_labels(G, pos)

# Exibir o grafo
plt.axis('off')
plt.show()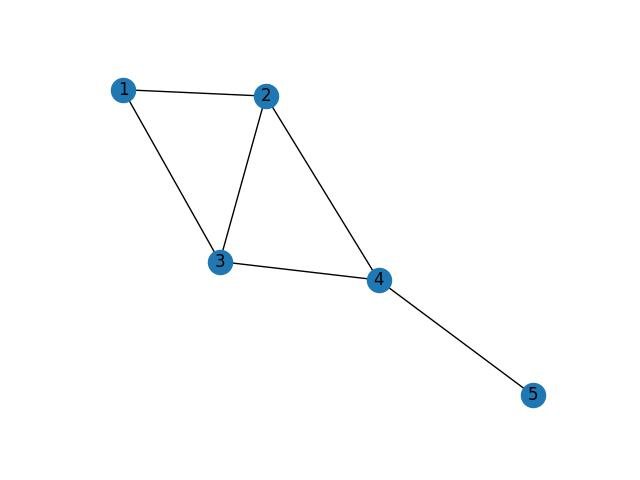

Neste exemplo, importamos a biblioteca networkx e criamos um objeto de grafo chamado G. Adicionamos nós ao grafo usando a função add_nodes_from() e adicionamos arestas usando a função add_edges_from().

Em seguida, definimos o layout do grafo usando a função spring_layout() do networkx. Essa função atribui posições aos nós usando um algoritmo baseado em física.

Depois, desenhamos os nós usando a função draw_networkx_nodes(), as arestas usando a função draw_networkx_edges() e adicionamos rótulos aos nós usando a

1.2.7.2.17 - Gráfico de cascata (waterfall chart)

O gráfico de cascata, também conhecido como waterfall chart, é uma visualização que ilustra como um valor inicial é alterado por uma série de fatores positivos e negativos, mostrando o impacto acumulado dessas mudanças. Ele é frequentemente usado para analisar o efeito líquido de diferentes componentes em um determinado valor, destacando contribuições individuais e variações ao longo do tempo.

Aqui estão os principais elementos de um gráfico de cascata:

• Valor inicial: É o valor de referência a partir do qual as mudanças serão calculadas. É geralmente mostrado como o primeiro nível no gráfico.
• Componentes: São os fatores positivos e negativos que contribuem para a mudança no valor inicial. Cada componente é representado por uma barra que se estende acima ou abaixo do nível anterior, dependendo se é positivo ou negativo.
• Níveis intermediários: São os níveis intermediários que mostram os valores acumulados à medida que os componentes são adicionados ou subtraídos do valor inicial. Eles ajudam a visualizar a mudança acumulada em cada etapa.
• Valor final: É o valor resultante após a consideração de todos os componentes. É mostrado como o último nível no gráfico.

Os gráficos de cascata são úteis para entender as mudanças cumulativas em um valor ao longo do tempo ou entre diferentes categorias. Eles são comumente usados em áreas como análise financeira, demonstrações de fluxo de caixa, análise de desempenho de vendas, entre outros.

Aqui está um exemplo de código Python usando a biblioteca matplotlib para criar um gráfico de cascata:

import matplotlib.pyplot as plt

# Dados dos componentes
componentes = ['Receita', 'Custos', 'Impostos', 'Despesas', 'Lucro']
valores = [100, -50, -20, -30, 40]

# Calcular os níveis intermediários
niveis = [0] + [sum(valores[:i+1]) for i in range(len(valores)-1)]

# Criar o gráfico de cascata
plt.bar(componentes, valores, bottom=niveis, color=['g', 'r', 'r', 'r', 'b'])

# Personalizar o gráfico
plt.title('Gráfico de Cascata')
plt.xlabel('Componentes')
plt.ylabel('Valor')
plt.grid(True)

# Exibir o gráfico
plt.show()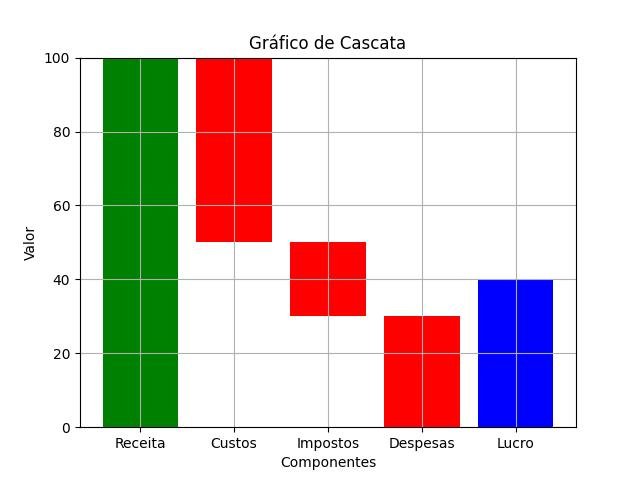

Neste exemplo, definimos os dados dos componentes e seus valores correspondentes. Os valores positivos são representados por barras verdes e os valores negativos por barras vermelhas. O valor final, que é a soma de todos os componentes, é mostrado como uma barra azul.

Calculamos os níveis intermediários somando os valores anteriores. A função plt.bar() é usada para criar as barras do gráfico de cascata, onde definimos os componentes, os valores, os níveis intermediários e as cores correspondentes.

Personalizamos o gráfico com um título, rótulos nos eixos x e y, e adicionamos grades para melhorar a legibilidade.

Você pode ajustar o exemplo de código de acordo com seus próprios dados e personalizações adicionais, como cores, rótulos, estilos de linha, entre outros. A biblioteca matplotlib oferece diversas opções para aprimorar a aparência do gráfico.

1.2.7.2.18 - Gráfico de controle

O gráfico de controle, também conhecido como gráfico de controle estatístico de processo (CEP - Controle Estatístico de Processo), é uma ferramenta utilizada na análise de dados para monitorar e controlar a qualidade de um processo ao longo do tempo. Ele é especialmente útil na identificação de variações inaceitáveis ​​no desempenho do processo, permitindo que ações corretivas sejam tomadas.

Existem vários tipos de gráficos de controle, mas os mais comumente utilizados são o gráfico de controle para dados individuais e o gráfico de controle para médias e amplitudes.

O gráfico de controle para dados individuais é usado quando temos apenas um valor observado em cada medição. Ele consiste em uma linha central que representa a média do processo e duas linhas de controle superior e inferior que são calculadas com base na variabilidade dos dados. Essas linhas de controle são geralmente definidas a uma distância fixa em relação à linha central, considerando a variabilidade esperada do processo. Quando um ponto ultrapassa essas linhas de controle, isso indica uma variação significativa que requer investigação.

O gráfico de controle para médias e amplitudes é usado quando temos várias medições em cada ponto de coleta. Ele é dividido em dois subgráficos: o gráfico de controle da média e o gráfico de controle da amplitude. O gráfico de controle da média mostra a média dos subgrupos de dados ao longo do tempo, enquanto o gráfico de controle da amplitude mostra a variação (amplitude) dentro de cada subgrupo. As linhas de controle são calculadas com base nas médias e amplitudes dos subgrupos e ajudam a monitorar a estabilidade do processo.

Aqui está um exemplo de código Python utilizando a biblioteca matplotlib para criar um gráfico de controle para dados individuais:

import numpy as np
import matplotlib.pyplot as plt

# Dados de exemplo
dados = np.array([5.1, 5.3, 5.2, 5.4, 5.6, 5.3, 5.5, 5.2, 5.4, 5.6, 5.2, 5.3, 5.5])

# Média e desvio padrão dos dados
media = np.mean(dados)
desvio_padrao = np.std(dados)

# Limite superior e inferior de controle
limite_superior = media + 3 * desvio_padrao
limite_inferior = media - 3 * desvio_padrao

# Plotagem do gráfico de controle
plt.plot(dados, 'bo-', label='Dados')
plt.axhline(media, color='r', linestyle='-', linewidth=2, label='Média')
plt.axhline(limite_superior, color='g', linestyle='--', linewidth=1, label='Limite Superior de Controle')
plt.axhline(limite_inferior, color='g', linestyle='--', linewidth=1, label='Limite Inferior de Controle')

# Configurações do gráfico
plt.title('Gráfico de Controle para Dados Individuais')
plt.xlabel('Amostras')
plt.ylabel('Valores')
plt.legend()

# Exibição do gráfico
plt.show()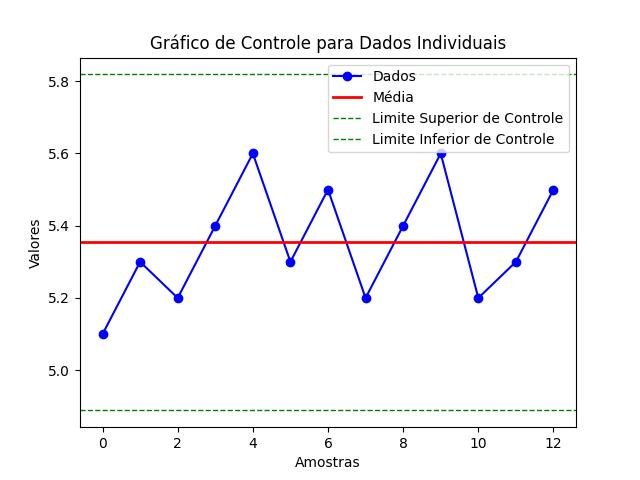

Neste exemplo, definimos um conjunto de dados de exemplo e calculamos a média e o desvio padrão dos dados. Com base nesses valores, calculamos as linhas de controle superior e inferior, que estão a três desvios padrão de distância da média.

Em seguida, usamos a função plt.plot() para traçar os pontos dos dados e a linha média. Também adicionamos as linhas de controle superior e inferior usando a função plt.axhline(), especificando a posição e o estilo das linhas.

Finalmente, personalizamos o gráfico com um título, rótulos nos eixos x e y, e uma legenda para indicar as diferentes linhas.

Você pode adaptar o exemplo de código para atender aos seus próprios dados, definindo seus próprios valores de limite e personalizando o estilo do gráfico de controle. A biblioteca matplotlib oferece várias opções para formatação e customização de gráficos.

1.2.7.2.19 - Gráfico de densidade

O gráfico de densidade é uma visualização que representa a distribuição de probabilidade de uma variável contínua. Ele é usado para entender a forma da distribuição dos dados e identificar a concentração de valores em diferentes regiões.

A área sob o gráfico de densidade representa a probabilidade de uma observação cair em uma determinada faixa de valores. Quanto maior a área em uma região específica, maior a probabilidade de encontrar valores nessa faixa.

Existem várias maneiras de criar um gráfico de densidade em Python. Uma das bibliotecas mais comumente usadas é o matplotlib, juntamente com o módulo seaborn. Aqui está um exemplo de código usando essas bibliotecas:

import seaborn as sns
import matplotlib.pyplot as plt

# Dados de exemplo
dados = [1.2, 1.5, 1.6, 1.8, 2.0, 2.2, 2.4, 2.6, 2.8, 3.0, 3.2, 3.3, 3.4]

# Criar o gráfico de densidade
sns.kdeplot(dados)

# Personalizar o gráfico
plt.title('Gráfico de Densidade')
plt.xlabel('Valores')
plt.ylabel('Densidade')

# Exibir o gráfico
plt.show()

Neste exemplo, utilizamos a função kdeplot da biblioteca seaborn para criar o gráfico de densidade. Passamos os dados de exemplo como argumento para a função.

Em seguida, personalizamos o gráfico definindo um título, rótulos nos eixos x e y.

Finalmente, utilizamos a função plt.show() para exibir o gráfico de densidade.

O gráfico de densidade pode ser útil para identificar se os dados estão concentrados em torno de um único pico (distribuição unimodal) ou se há múltiplos picos (distribuição multimodal). Ele também permite visualizar a forma da distribuição, como assimetrias ou caudas longas.

Além do seaborn, outras bibliotecas como numpy e scipy também fornecem funções para criar gráficos de densidade. A escolha da biblioteca depende das suas preferências e das funcionalidades específicas que você deseja utilizar.

1.2.7.2.20 - Gráfico de heat map

O gráfico de heatmap, ou mapa de calor, é uma representação visual de dados onde as cores são usadas para mostrar a intensidade ou magnitude de uma variável em uma matriz de valores. É frequentemente usado para visualizar a relação entre duas variáveis em uma grade ou tabela.

A biblioteca matplotlib em Python oferece suporte para criar gráficos de heatmap. Aqui está um exemplo de código que utiliza a biblioteca matplotlib para criar um gráfico de heatmap:

import numpy as np
import matplotlib.pyplot as plt

# Dados de exemplo
dados = np.random.rand(5, 5)  # Matriz de valores aleatórios 5x5

# Criar o gráfico de heatmap
plt.imshow(dados, cmap='hot', interpolation='nearest')

# Personalizar o gráfico
plt.title('Gráfico de Heatmap')
plt.colorbar()

# Exibir o gráfico
plt.show()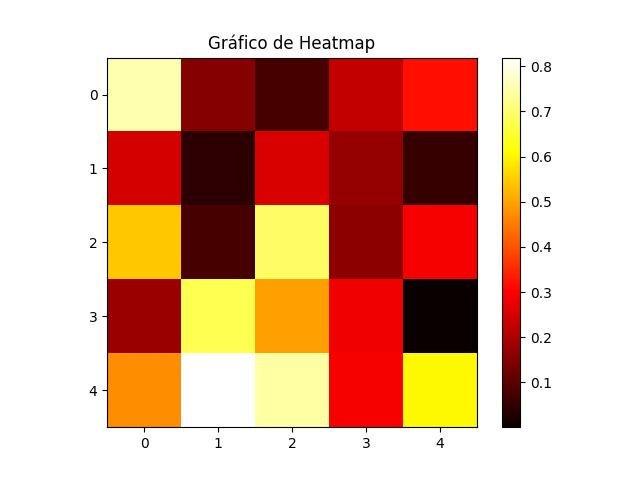

Neste exemplo, usamos a função imshow() para criar o gráfico de heatmap. Passamos a matriz de valores de exemplo (dados) como argumento para a função. Também especificamos a paleta de cores usando o parâmetro cmap, que neste caso foi definido como 'hot' para usar uma paleta de cores quentes.

Além disso, personalizamos o gráfico com um título e adicionamos uma barra de cores usando a função colorbar() para indicar a escala de cores e a correspondência entre valores e cores.

O gráfico de heatmap é especialmente útil quando você tem uma matriz de dados e deseja visualizar a distribuição e os padrões dessa matriz. Ele pode ser usado em várias áreas, como análise de dados, ciência de dados, visualização de correlações, análise de desempenho, entre outros.

Você pode adaptar o exemplo de código para os seus próprios dados, modificando a matriz dados e personalizando outros aspectos do gráfico, como título, rótulos dos eixos, paleta de cores e interpolação (parâmetro interpolation). A biblioteca matplotlib oferece diversas opções de personalização para gráficos de heatmap.

1.2.7.3 - Gráficos compostos

Gráficos compostos, também conhecidos como gráficos combinados ou gráficos múltiplos, referem-se à criação de visualizações que combinam diferentes tipos de gráficos em uma única figura. Essa técnica é usada para mostrar múltiplas informações ou aspectos de um conjunto de dados em um único espaço visual.

A ideia por trás dos gráficos compostos é aproveitar os pontos fortes de diferentes tipos de gráficos para fornecer uma representação mais abrangente e compreensível dos dados. Por exemplo, você pode combinar um gráfico de linha com um gráfico de barras, um gráfico de área com um gráfico de dispersão, ou qualquer outra combinação que seja relevante para os dados em questão.

Existem várias razões pelas quais os gráficos compostos são úteis:

• Visualização de diferentes variáveis: Ao combinar diferentes tipos de gráficos, é possível exibir e comparar múltiplas variáveis ao mesmo tempo. Isso ajuda a identificar padrões, relações e tendências nos dados que podem não ser evidentes em uma única visualização.
• Contextualização dos dados: Gráficos compostos permitem incluir informações adicionais ou contextuais para auxiliar na interpretação dos dados. Por exemplo, você pode adicionar linhas de referência, anotações, legendas ou outras informações relevantes.
• Comparação visual: Ao colocar diferentes gráficos lado a lado, é possível fazer comparações visuais diretas entre eles. Isso é especialmente útil para destacar diferenças, semelhanças ou padrões entre diferentes conjuntos de dados ou categorias.
• Comunicação efetiva: Gráficos compostos podem fornecer uma representação visual mais rica e informativa dos dados, o que facilita a comunicação de informações complexas de maneira clara e concisa.

A criação de gráficos compostos pode ser feita usando bibliotecas de visualização de dados em Python, como matplotlib e seaborn. Essas bibliotecas fornecem recursos flexíveis para combinar diferentes tipos de gráficos em uma única figura, permitindo que você personalize a aparência e o layout do gráfico composto de acordo com suas necessidades.

Ao criar gráficos compostos, é importante garantir que a combinação de gráficos seja lógica e facilite a compreensão dos dados. É fundamental escolher os tipos de gráficos apropriados e posicionar os elementos de forma clara e organizada. A legibilidade e a clareza da informação devem ser priorizadas para garantir que os usuários possam extrair insights significativos dos gráficos compostos.

Existem várias maneiras de combinar diferentes tipos de gráficos para criar gráficos compostos. Alguns dos tipos mais comuns de gráficos compostos são:

• Gráfico de linhas com gráfico de barras: Essa combinação é útil quando se deseja comparar uma tendência ao longo do tempo (gráfico de linhas) com valores específicos em pontos de dados individuais (gráfico de barras).
• Gráfico de dispersão com linha de regressão: Isso permite visualizar a relação entre duas variáveis usando um gráfico de dispersão e, ao mesmo tempo, traçar uma linha de regressão para identificar a tendência geral dos dados.
• Gráfico de barras empilhadas: Nesse tipo de gráfico, as barras são divididas em segmentos, representando diferentes categorias ou grupos dentro de cada barra. Isso é útil para comparar a distribuição de uma variável em diferentes grupos.
• Gráfico de área empilhada: Semelhante ao gráfico de barras empilhadas, mas usando áreas coloridas em vez de barras para representar as proporções ou distribuição de diferentes categorias ou grupos.
• Gráfico de barras e gráfico de setores: Essa combinação é útil quando se deseja exibir valores absolutos (gráfico de barras) e proporções relativas (gráfico de setores) de diferentes categorias em um único gráfico.
• Gráfico de dispersão com tamanho de bolhas: Nesse tipo de gráfico, os pontos de dados são exibidos em um gráfico de dispersão, mas o tamanho das bolhas é usado para representar uma terceira variável. Isso permite visualizar a relação entre duas variáveis e ao mesmo tempo mostrar a magnitude de uma terceira variável.

Esses são apenas alguns exemplos de combinações de gráficos compostos. A escolha dos tipos de gráficos a serem combinados depende dos dados e das informações que você deseja comunicar. A criatividade e a compreensão dos dados são fundamentais para criar gráficos compostos eficazes e informativos.

1.2.7.3.1 - Gráfico de linhas com gráfico de barras

O gráfico de linhas com gráfico de barras é uma combinação visual de dois tipos de gráficos: o gráfico de linhas e o gráfico de barras. Essa combinação é útil quando se deseja mostrar uma tendência ao longo do tempo usando um gráfico de linhas e, ao mesmo tempo, exibir valores específicos em pontos de dados individuais usando um gráfico de barras.

O gráfico de linhas é adequado para visualizar uma tendência contínua ou progressão ao longo do eixo x, geralmente representando o tempo. Os pontos de dados são conectados por uma linha, mostrando a variação da variável ao longo do tempo ou de outro fator contínuo.

Por outro lado, o gráfico de barras é usado para representar valores discretos ou categorias distintas. Cada barra representa um valor específico em uma categoria ou grupo. Essas barras podem ser organizadas lado a lado ou empilhadas para comparar os valores entre as categorias.

Ao combinar esses dois tipos de gráficos, é possível mostrar a tendência geral dos dados ao longo do tempo (gráfico de linhas) e, ao mesmo tempo, destacar valores específicos em momentos específicos (gráfico de barras).

Aqui está um exemplo de código em Python usando as bibliotecas matplotlib e seaborn para criar um gráfico de linhas com gráfico de barras:

import matplotlib.pyplot as plt
import seaborn as sns

# Dados de exemplo
anos = [2010, 2011, 2012, 2013, 2014, 2015]
valores_linha = [50, 60, 55, 70, 80, 75]
valores_barra = [45, 55, 60, 65, 70, 75]

# Criar a figura e os eixos
fig, ax1 = plt.subplots()

# Plotar o gráfico de linhas
ax1.plot(anos, valores_linha, marker='o', color='blue')
ax1.set_xlabel('Anos')
ax1.set_ylabel('Valores Linha', color='blue')

# Plotar o gráfico de barras
ax2 = ax1.twinx()
ax2.bar(anos, valores_barra, alpha=0.5, color='red')
ax2.set_ylabel('Valores Barra', color='red')

# Personalizar o gráfico
plt.title('Gráfico de Linhas com Gráfico de Barras')
plt.grid(True)

# Exibir o gráfico
plt.show()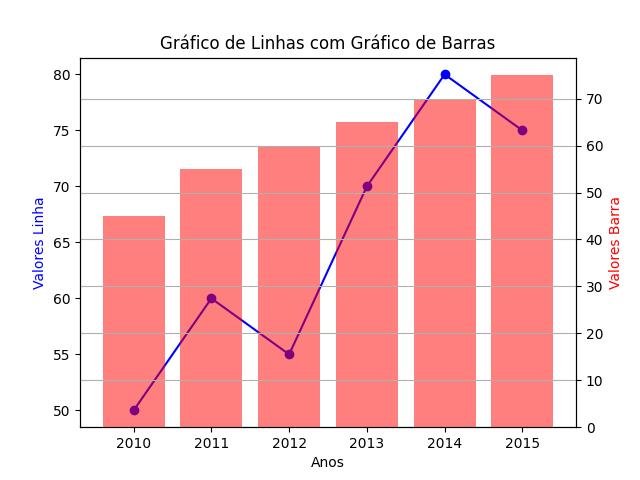

Nesse exemplo, temos os dados de exemplo representando os anos e os valores correspondentes para o gráfico de linhas (valores_linha) e o gráfico de barras (valores_barra).

Usamos a função plt.subplots() para criar a figura e os eixos. Em seguida, plotamos o gráfico de linhas usando a função ax1.plot() e personalizamos os rótulos dos eixos x e y para o gráfico de linhas.

Depois disso, criamos o segundo conjunto de eixos ax2 usando o método ax1.twinx(). Em seguida, usamos a função ax2.bar() para plotar o gráfico de barras e definimos a cor das barras como vermelho.

Por fim, personalizamos o gráfico adicionando um título e ativando as grades. O

1.2.7.3.2 - Gráfico de dispersão com linha de regressão

O gráfico de dispersão com linha de regressão é uma combinação visual de um gráfico de dispersão e uma linha de regressão. Essa combinação é útil quando se deseja visualizar a relação entre duas variáveis usando o gráfico de dispersão e, ao mesmo tempo, traçar uma linha de regressão para identificar a tendência geral dos dados.

O gráfico de dispersão é usado para representar pares de valores em um plano cartesiano, onde cada ponto de dados é exibido como um ponto no gráfico. Ele é adequado para identificar a relação ou a correlação entre duas variáveis contínuas.

A linha de regressão, por sua vez, é uma linha que melhor se ajusta aos pontos de dados no gráfico de dispersão. Ela é calculada usando técnicas estatísticas, como regressão linear, para modelar a tendência geral dos dados e fornecer uma estimativa da relação entre as variáveis.

Aqui está um exemplo de código em Python usando as bibliotecas matplotlib e seaborn para criar um gráfico de dispersão com linha de regressão:

import matplotlib.pyplot as plt
import seaborn as sns

# Dados de exemplo
x = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
y = [3, 5, 7, 8, 9, 10, 11, 13, 15, 16]

# Criar o gráfico de dispersão com linha de regressão
sns.regplot(x=x, y=y)

# Personalizar o gráfico
plt.title('Gráfico de Dispersão com Linha de Regressão')
plt.xlabel('Variável X')
plt.ylabel('Variável Y')

# Exibir o gráfico
plt.show()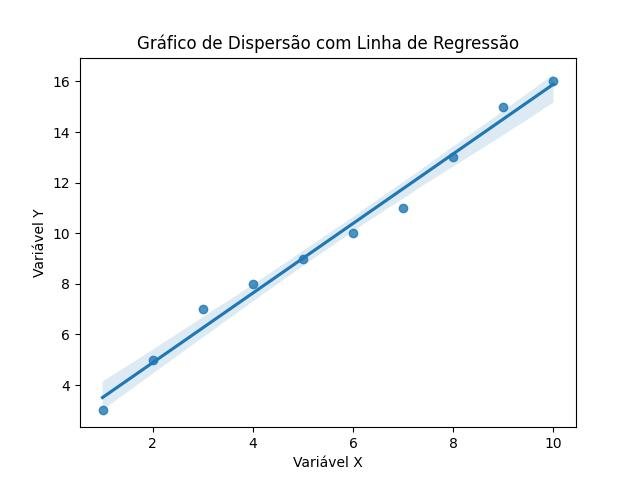

Nesse exemplo, temos os dados de exemplo representando as variáveis x e y. Usamos a função sns.regplot() do seaborn para criar o gráfico de dispersão com linha de regressão.

A função sns.regplot() calcula automaticamente a linha de regressão e a plota no gráfico de dispersão. Ela usa regressão linear por padrão, mas você pode especificar outros métodos de regressão, se necessário.

Em seguida, personalizamos o gráfico adicionando um título, rótulos para os eixos x e y. Depois disso, chamamos plt.show() para exibir o gráfico.

O gráfico de dispersão com linha de regressão ajuda a visualizar a tendência geral dos dados e a identificar a direção e a intensidade da relação entre as variáveis. A linha de regressão pode ser usada para fazer previsões ou inferências com base nos dados disponíveis.

1.2.7.3.3 - Gráfico de barras empilhadas

O gráfico de barras empilhadas é uma representação visual que permite comparar a distribuição de uma variável entre diferentes categorias ou grupos. Nesse tipo de gráfico, as barras são empilhadas uma sobre a outra, mostrando a contribuição de cada categoria para o total.

Esse tipo de gráfico é útil quando se deseja visualizar não apenas os valores absolutos de cada categoria, mas também a proporção relativa de cada categoria dentro do total. Isso facilita a comparação das contribuições individuais e a identificação de padrões ou tendências.

Aqui está um exemplo de código em Python usando as bibliotecas matplotlib e seaborn para criar um gráfico de barras empilhadas:

import matplotlib.pyplot as plt

# Dados de exemplo
categorias = ['A', 'B', 'C', 'D']
valores1 = [10, 15, 12, 8]
valores2 = [5, 8, 6, 9]
valores3 = [7, 9, 11, 6]

# Criar o gráfico de barras empilhadas
plt.bar(categorias, valores1, label='Grupo 1')
plt.bar(categorias, valores2, bottom=valores1, label='Grupo 2')
plt.bar(categorias, valores3, bottom=[i+j for i,j in zip(valores1, valores2)], label='Grupo 3')

# Personalizar o gráfico
plt.title('Gráfico de Barras Empilhadas')
plt.xlabel('Categorias')
plt.ylabel('Valores')
plt.legend()

# Exibir o gráfico
plt.show()

Nesse exemplo, temos os dados de exemplo representando as categorias (categorias) e os valores correspondentes para três grupos (valores1, valores2 e valores3).

Usamos a função plt.bar() para criar as barras empilhadas. Cada chamada dessa função representa um grupo diferente, onde passamos os valores correspondentes e usamos o parâmetro bottom para especificar a base das barras empilhadas. A base é calculada somando os valores dos grupos anteriores.

Depois disso, personalizamos o gráfico adicionando um título, rótulos para os eixos x e y, e uma legenda para identificar cada grupo.

O gráfico de barras empilhadas permite visualizar as contribuições relativas de cada categoria dentro do total. É útil para comparar a distribuição de uma variável entre diferentes grupos e identificar padrões ou discrepâncias entre as categorias.

1.2.7.3.4 - Gráfico de área empilhada

Com certeza! O gráfico de área empilhada é uma representação visual que permite comparar a distribuição de diferentes categorias ou grupos ao longo de um eixo, mostrando como as áreas coloridas se acumulam uma sobre a outra.

Esse tipo de gráfico é semelhante ao gráfico de barras empilhadas, mas em vez de usar barras retangulares, ele usa áreas coloridas para representar as proporções ou distribuição de cada categoria em relação ao total.

O gráfico de área empilhada é útil quando se deseja visualizar tanto a contribuição individual de cada categoria quanto a distribuição geral de todas as categorias. Ele permite analisar as mudanças nas proporções ao longo do tempo ou em diferentes grupos, destacando as áreas de maior ou menor contribuição.

Aqui está um exemplo de código em Python usando as bibliotecas matplotlib e seaborn para criar um gráfico de área empilhada:

import matplotlib.pyplot as plt

# Dados de exemplo
categorias = ['A', 'B', 'C', 'D']
valores1 = [10, 15, 12, 8]
valores2 = [5, 8, 6, 9]
valores3 = [7, 9, 11, 6]

# Criar o gráfico de área empilhada
plt.stackplot(categorias, valores1, valores2, valores3, labels=['Grupo 1', 'Grupo 2', 'Grupo 3'])

# Personalizar o gráfico
plt.title('Gráfico de Área Empilhada')
plt.xlabel('Categorias')
plt.ylabel('Valores')
plt.legend(loc='upper left')

# Exibir o gráfico
plt.show()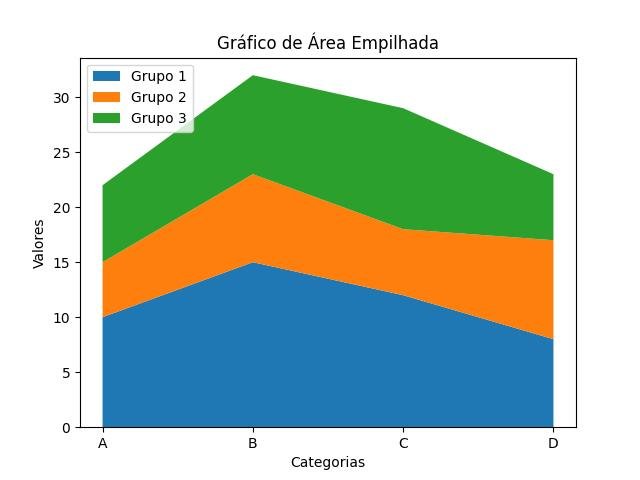

Nesse exemplo, temos os dados de exemplo representando as categorias (categorias) e os valores correspondentes para três grupos (valores1, valores2 e valores3).

Usamos a função plt.stackplot() para criar o gráfico de área empilhada. Passamos as categorias e os valores de cada grupo como argumentos, e usamos o parâmetro labels para definir as legendas para cada grupo.

Depois disso, personalizamos o gráfico adicionando um título, rótulos para os eixos x e y, e uma legenda para identificar cada grupo.

O gráfico de área empilhada permite visualizar a distribuição de diferentes categorias em relação ao total. É útil para mostrar as proporções relativas das categorias e identificar quais categorias têm maior ou menor contribuição. Além disso, ele permite analisar as mudanças nas proporções ao longo do tempo ou em diferentes grupos.

1.2.7.3.5 - Gráfico de barras e gráfico de setores

Certamente! O gráfico de barras e o gráfico de setores (ou gráfico de pizza) são dois tipos populares de gráficos usados para visualizar dados categorizados. Eles têm finalidades diferentes, mas ambos são eficazes na representação de informações em formato visual.

O gráfico de barras é adequado para comparar valores entre diferentes categorias. Ele consiste em barras retangulares que são proporcionais aos valores que representam. Cada categoria é representada por uma barra individual, e a altura da barra indica o valor correspondente.

Por outro lado, o gráfico de setores é ideal para mostrar a composição ou a distribuição relativa de partes em relação a um todo. Ele usa setores circulares para representar cada categoria, onde o tamanho do setor é proporcional à proporção da categoria em relação ao total. Os setores são agrupados em um círculo completo que representa o total.

Aqui está um exemplo de código em Python usando a biblioteca matplotlib para criar um gráfico de barras e um gráfico de setores:

import matplotlib.pyplot as plt

# Dados de exemplo
categorias = ['A', 'B', 'C', 'D']
valores = [20, 35, 30, 15]

# Gráfico de barras
plt.subplot(121)
plt.bar(categorias, valores)
plt.title('Gráfico de Barras')

# Gráfico de setores
plt.subplot(122)
plt.pie(valores, labels=categorias, autopct='%1.1f%%')
plt.title('Gráfico de Setores')

# Ajustar o layout
plt.tight_layout()

# Exibir os gráficos
plt.show()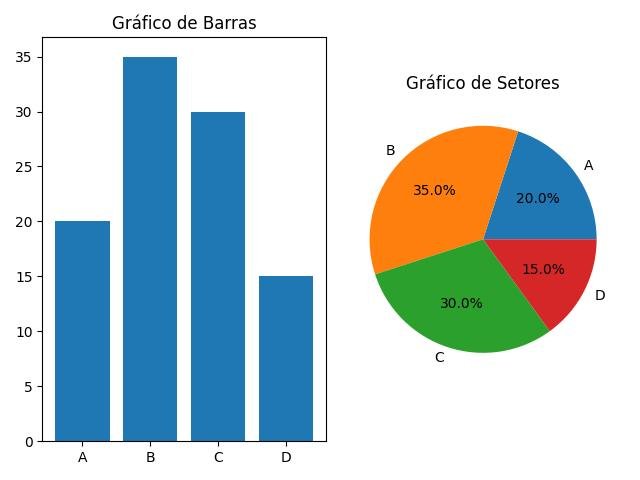

Nesse exemplo, temos os dados de exemplo representando as categorias (categorias) e os valores correspondentes (valores).

Usamos a função plt.bar() para criar o gráfico de barras, passando as categorias e os valores como argumentos.

Para o gráfico de setores, usamos a função plt.pie(). Passamos os valores e as categorias como argumentos e usamos o parâmetro autopct para formatar as porcentagens exibidas nos setores.

Em seguida, ajustamos o layout usando plt.tight_layout() para evitar sobreposição de elementos nos gráficos.

Por fim, chamamos plt.show() para exibir os gráficos.

O gráfico de barras é eficaz para comparar valores entre categorias, enquanto o gráfico de setores destaca a composição ou a distribuição relativa das categorias em relação ao todo. A escolha entre esses gráficos depende do objetivo de comunicação e do tipo de informação que se deseja destacar.

1.2.7.3.6 - Gráfico de dispersão com tamanho de bolhas

O gráfico de dispersão com tamanho de bolhas (bubble chart) é uma variação do gráfico de dispersão em que o tamanho das bolhas é usado para representar uma terceira variável. Ele é útil para visualizar a relação entre duas variáveis contínuas, como em um gráfico de dispersão tradicional, enquanto o tamanho das bolhas representa uma medida adicional.

Nesse tipo de gráfico, cada ponto no gráfico de dispersão é representado por uma bolha, onde a posição horizontal e vertical das bolhas indica os valores das duas variáveis em análise, e o tamanho das bolhas é determinado por uma terceira variável.

O gráfico de dispersão com tamanho de bolhas permite exibir a relação entre as duas variáveis principais, enquanto adiciona uma dimensão extra por meio do tamanho das bolhas. Isso pode fornecer informações adicionais sobre a intensidade ou a magnitude da terceira variável.

Aqui está um exemplo de código em Python usando as bibliotecas matplotlib e seaborn para criar um gráfico de dispersão com tamanho de bolhas:

import matplotlib.pyplot as plt
import seaborn as sns

# Dados de exemplo
x = [1, 2, 3, 4, 5]
y = [10, 15, 7, 12, 8]
sizes = [30, 50, 20, 40, 10]

# Criar o gráfico de dispersão com tamanho de bolhas
plt.scatter(x, y, s=sizes)

# Personalizar o gráfico
plt.title('Gráfico de Dispersão com Tamanho de Bolhas')
plt.xlabel('Variável X')
plt.ylabel('Variável Y')

# Exibir o gráfico
plt.show()

Nesse exemplo, temos os dados de exemplo representando as variáveis x e y, e também a variável sizes, que representa os tamanhos das bolhas.

Usamos a função plt.scatter() para criar o gráfico de dispersão com tamanho de bolhas. Passamos os valores de x e y como argumentos, e especificamos os tamanhos das bolhas usando o parâmetro s e fornecendo a lista de sizes.

Em seguida, personalizamos o gráfico adicionando um título, rótulos para os eixos x e y.

O gráfico de dispersão com tamanho de bolhas ajuda a visualizar a relação entre as duas variáveis principais e a terceira variável representada pelo tamanho das bolhas. É útil para identificar padrões ou tendências e também para destacar a magnitude ou a intensidade da terceira variável em relação aos valores das duas variáveis principais.