Estatistica Avançada
Carregando, aguarde alguns segundos.
2 - Análise Exploratória de Dados
2.1 Gráficos básicos e visualizações avançadas
2.2 Medidas de tendência central e dispersão robustas
2.3 Análise de correlação e covariância multivariada
2.4 Análise de componentes principais e análise fatorial
Neste capítulo, adentraremos no mundo das técnicas avançadas de visualização, que nos permitem explorar e comunicar de maneira eficaz os padrões complexos e relacionamentos presentes nos dados.
- Gráficos básicos e visualizações avançadas: descobriremos como representar dados multivariados por meio de gráficos de dispersão em várias dimensões, como criar gráficos interativos e dinâmicos para explorar grandes volumes de dados, e como utilizar técnicas avançadas de visualização, como mapas de calor, diagramas de Sankey e gráficos de redes, para revelar padrões complexos e conexões entre as variáveis.
- Medidas de tendência central e dispersão robustas: aprofundaremos nosso conhecimento sobre medidas de tendência central e dispersão, essenciais para resumir e compreender a distribuição dos dados. No entanto, não nos limitaremos apenas às medidas tradicionais. Exploraremos medidas robustas, que são menos sensíveis a valores atípicos e distribuições não normais. Aprenderemos como utilizar essas medidas para obter uma visão mais confiável dos dados e para identificar possíveis anomalias ou desvios significativos.
- Análise de correlação e covariância multivariada: aprofundaremos na análise de correlação e covariância multivariada. Exploraremos diferentes métodos para avaliar a relação entre variáveis e como identificar correlações significativas em conjuntos de dados de alta dimensão. Além disso, discutiremos a interpretação e o uso de matrizes de covariância e correlação em problemas de modelagem estatística e análise multivariada.
- Análise de componentes principais e análise fatorial: mergulharemos na análise de componentes principais (PCA) e análise fatorial, técnicas poderosas para redução de dimensionalidade e extração de informações relevantes em conjuntos de dados complexos. Aprenderemos como identificar e interpretar os principais componentes que explicam a maior parte da variabilidade dos dados, bem como como utilizar a análise fatorial para identificar estruturas latentes e reduzir a complexidade dos dados.
Ao explorar os tópicos abordados neste capítulo, você desenvolverá habilidades avançadas em análise exploratória de dados, permitindo que você identifique padrões ocultos, compreenda relações complexas entre as variáveis e obtenha insights valiosos dos dados.
Essas técnicas serão fundamentais para sua jornada como um estatístico ou cientista de dados, capacitando-o a tomar decisões informadas e a extrair conhecimento significativo dos dados disponíveis.
2.1 - Gráficos básicos e visualizações avançadas
A análise exploratória de dados desempenha um papel fundamental na compreensão e extração de informações valiosas dos conjuntos de dados.
É por meio dessa análise inicial que podemos obter insights iniciais, identificar padrões, tendências e anomalias nos dados, além de obter uma compreensão mais profunda da natureza dos dados que estamos trabalhando.
Os exemplos de código Python a seguir utilizam as bibliotecas Matplotlib e Numpy para criar gráficos e visualizações avançadas que podem ajudar a identificar padrões, tendências e anomalias nos dados.
Primeiro importamos as bibliotecas matplotlib.pyplot e numpy:
import matplotlib.pyplot as plt
import numpy as npCriamos as variáveis x e y que utilizaremos.
A variável x assume valores entre 0 e 10 com um incremento de 0.1.
A variável y assume n valores aleatórios entre 0 e 0.2, onde n é a quantidade de valores em x, somados aos seno de x.
x = np.arange(0, 10, 0.1)
y = np.random.normal(0, 0.2, len(x)) + np.sin(x)2.1.1 - Gráficos Básicos
Os códigos dos exemplos a seguir criam diferentes tipos de gráficos básicos que podem ser úteis na análise exploratória de dados.
- O gráfico de linha ajuda a identificar tendências nos dados.
- O gráfico de dispersão pode revelar padrões ou anomalias.
- O gráfico de histograma mostra a distribuição dos valores.
- O gráfico de caixa ajuda a identificar outliers.
- O gráfico de barras é útil para visualizar categorias ou frequências.
Você pode adaptar esses códigos de acordo com os seus dados específicos e explorar outras opções de gráficos oferecidas pela biblioteca Matplotlib para criar visualizações avançadas de acordo com suas necessidades.
2.1.1.1 - Gráfico de linhas
O gráfico de linhas é utilizado para visualizar a tendência dos dados, com os pontos de x e y nos eixos das abcissas e ordenadas, respectivamente:
- O método plot() cria um gráfico de linhas com os dados de x e y nos eixos das abcissas e ordenadas, respectivamente.
- O método title() define o título do gráfico.
- O método xlabel() define o nome do eixo das abcissas.
- O método ylabel() define o nome do eixo das ordenadas.
- O método show() mostra o gráfico.
plt.plot(x, y)
plt.title('Gráfico de Linha')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()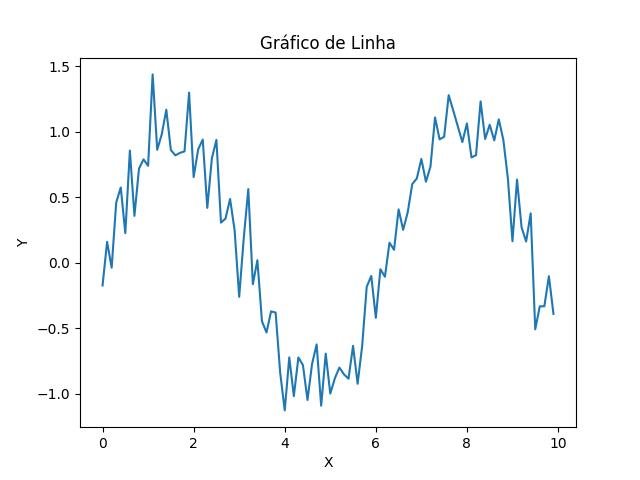
2.1.1.2 - Gráfico de dispersão
Gráfico de dispersão para identificar padrões e anomalias.
- O método scatter() cria um gráfico de dispersão com os dados de x e y nos eixos das abcissas e ordenadas, respectivamente.
plt.scatter(x, y)
plt.title('Gráfico de Dispersão')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()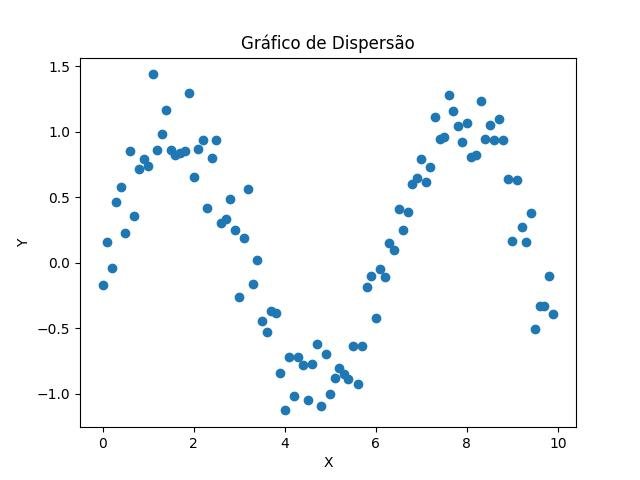
2.1.1.3 - Gráfico de histograma
Gráfico de histograma para visualizar a distribuição dos dados usando as quantidades de valores de y em x:
- O método hist() cria um gráfico de histograma com os dados de y no eixo das ordenadas, e no eixo das abcissas as quantidades de cada valor.
plt.hist(y, bins=20)
plt.title('Histograma')
plt.xlabel('Valores')
plt.ylabel('Frequência')
plt.show()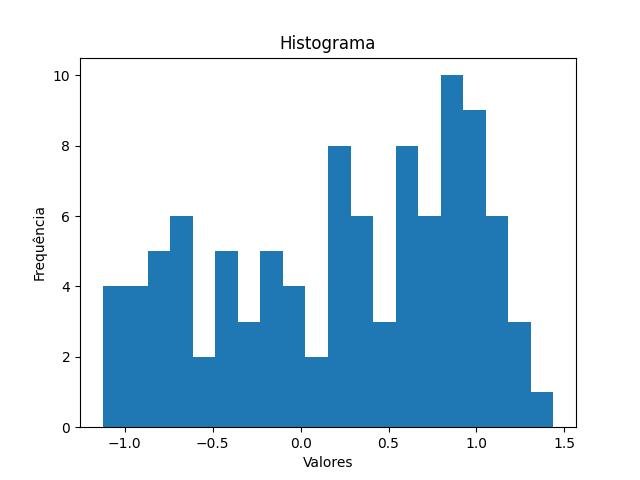
2.1.1.4 - Gráfico de caixa
Gráfico de caixa para identificar outliers:
- O método boxplot() cria um gráfico de caixa com os dados de y no eixo das ordenadas.
plt.boxplot(y)
plt.title('Gráfico de Caixa')
plt.ylabel('Valores')
plt.show()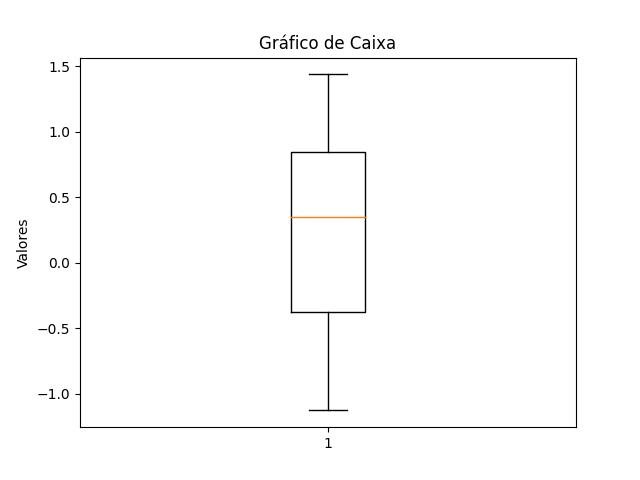
2.1.1.5 - Gráfico de barras
O gráfico de barras é utilizado para visualizar categorias ou frequências.
No exemplo o método bar() cria um gráfico de barras com os dados de x_categorias e y_contagem nos eixos das abcissas e ordenadas, respectivamente.
x_categorias = ['A', 'B', 'C', 'D', 'E']
y_contagem = [25, 40, 30, 10, 15]
plt.title('Gráfico de Barras')
plt.xlabel('Categorias')
plt.ylabel('Contagem')
plt.bar(x_categorias, y_contagem)
plt.show()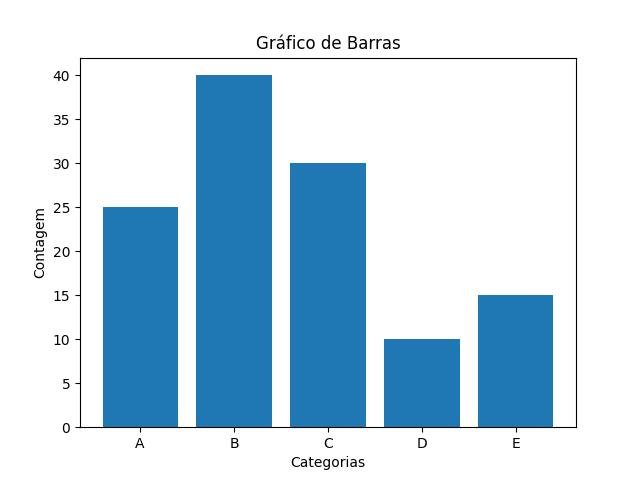
2.1.2 - Visualizações Avançadas
Agora iremos além dos gráficos básicos e nos aprofundamos em técnicas avançadas de visualização.
Com o auxílio dessas visualizações, poderemos explorar e comunicar de maneira eficaz os padrões complexos e relacionamentos presentes nos dados.
Ao utilizar gráficos e visualizações avançadas, somos capazes de revelar informações ocultas e insights significativos que podem passar despercebidos apenas por meio de análises numéricas.
Por exemplo, gráficos de dispersão multivariados nos permitem identificar correlações complexas entre várias variáveis e entender as relações entre elas.
Gráficos interativos e dinâmicos nos possibilitam explorar grandes volumes de dados de forma eficiente e identificar padrões em diferentes níveis de detalhes.
Além disso, exploraremos técnicas avançadas de visualização, como mapas de calor, diagramas de Sankey e gráficos de redes, que nos permitem representar e analisar dados complexos em formatos visualmente intuitivos.
A seguir estão exemplos de código das técnicas citadas acima usando as bibliotecas matplotlib, seaborn e networkx no Python:
Adapte esses códigos de acordo com seus dados específicos e personalize os parâmetros para atender às suas necessidades.
Essas bibliotecas oferecem uma variedade de opções de personalização para criar visualizações avançadas e informativas.
2.1.2.1 - Mapa de calor
Mapa de calor (Heatmap) usando a biblioteca seaborn:
# plt e np já foram importados
import seaborn as sns
# Dados de exemplo
data = np.random.rand(10, 10)
# Criação do mapa de calor
sns.heatmap(data, cmap='YlOrRd')
plt.title('Mapa de Calor')
plt.show()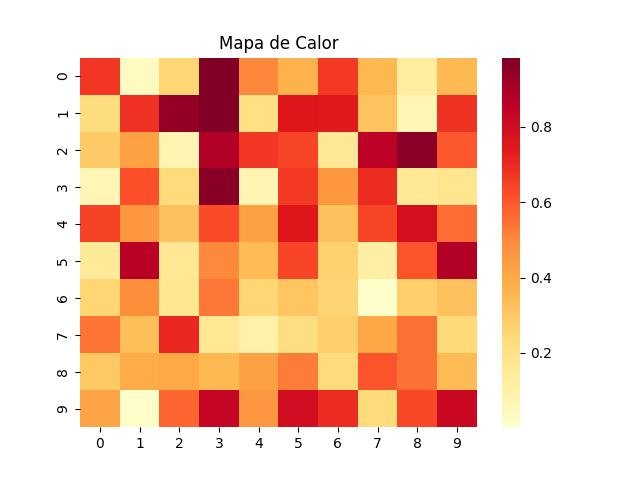
2.1.2.2 - Diagrama de Sankey
Diagrama de Sankey usando o módulo sankey da biblioteca matplotlib:
- A classe Sankey é usada para criar diagramas de Sankey.
- O método add() adiciona os dados de fluxos e rotulos no diagrama de Sankey.
- O método finish() finaliza o diagrama de Sankey.
from matplotlib.sankey import Sankey
# Dados de exemplo
fluxos = [0.25, 0.15, 0.4, 0.2]
rotulos = ['A', 'B', 'C', 'D']
# Criação do diagrama de Sankey
sankey = Sankey()
sankey.add(flows=fluxos, labels=rotulos, orientations=[0, 0, 1, -1])
diagramas = sankey.finish()
plt.title('Diagrama de Sankey')
plt.show()
2.1.2.3 - Gráfico de rede
Gráfico de rede usando a biblioteca networkx:
- A classe DiGraph é usada para criar gráficos de rede.
- O método add_edge() adiciona arestas e atributos aos gráficos de rede.
- O método draw() desenha o gráfico de rede.
import networkx as nx
# Criação de um grafo direcionado
G = nx.DiGraph()
# Adição de arestas e atributos
G.add_edge('A', 'B', weight=0.6)
G.add_edge('A', 'C', weight=0.2)
G.add_edge('B', 'C', weight=0.1)
G.add_edge('C', 'D', weight=0.7)
# Criação do layout do gráfico
pos = nx.spring_layout(G)
# Desenho do gráfico de rede
nx.draw(
G, pos, with_labels=True, node_color='lightblue',
node_size=2000, edge_color='gray', width=2,
arrowsize=20, arrowstyle='fancy')
labels = nx.get_edge_attributes(G, 'weight')
nx.draw_networkx_edge_labels(G, pos, edge_labels=labels)
plt.title('Gráfico de Rede')
plt.show()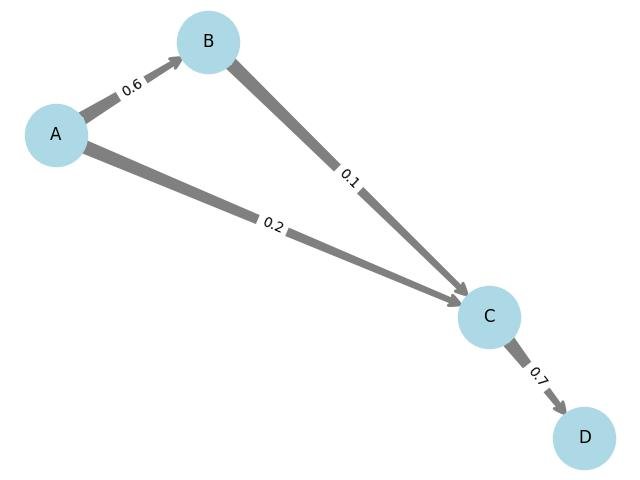
2.1.2.4 - detecção de comunidades
Essas técnicas nos ajudam a identificar padrões de interconexão, fluxos de dados e agrupamentos que podem fornecer insights valiosos para a tomada de decisões e a compreensão dos fenômenos subjacentes.
Para identificar padrões de interconexão, fluxos de dados e agrupamentos, você pode usar a biblioteca NetworkX em Python.
Aqui está um exemplo de código que utiliza algoritmos de detecção de comunidades para identificar agrupamentos em um grafo:
import networkx as nx
import matplotlib.pyplot as plt
import community
# Criação de um grafo direcionado
G = nx.Graph()
# Adição de arestas
G.add_edge('A', 'B')
G.add_edge('A', 'C')
G.add_edge('B', 'C')
G.add_edge('C', 'D')
G.add_edge('D', 'E')
G.add_edge('E', 'F')
G.add_edge('F', 'D')
# Detecção de comunidades usando o algoritmo Louvain
partition = community.best_partition(G)
# Criação do layout do gráfico
pos = nx.spring_layout(G)
# Desenho do gráfico de rede com cores representando as comunidades
nx.draw_networkx_nodes(G, pos, node_color=list(partition.values()), cmap='viridis', node_size=200)
nx.draw_networkx_edges(G, pos, alpha=0.5)
plt.title('Gráfico de Rede com Detecção de Comunidades')
plt.show()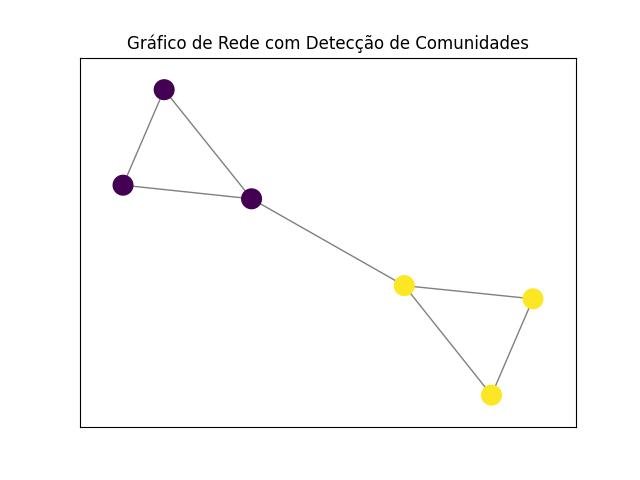
2.1.2.5 - Louvain
Neste exemplo, o algoritmo Louvain é usado para detectar as comunidades no grafo, e as cores dos nós representam a associação de cada nó a uma comunidade específica.
import networkx as nx
import matplotlib.pyplot as plt
from community import community_louvain
# Criação de um grafo direcionado
G = nx.Graph()
# Adição de arestas
G.add_edge('A', 'B')
G.add_edge('A', 'C')
G.add_edge('B', 'C')
G.add_edge('C', 'D')
G.add_edge('D', 'E')
G.add_edge('E', 'F')
G.add_edge('F', 'D')
# Detecção de comunidades usando o algoritmo Louvain
partition = community_louvain.best_partition(G)
# Criação do layout do gráfico
pos = nx.spring_layout(G)
# Desenho do gráfico de rede com cores representando as comunidades
nx.draw_networkx_nodes(G, pos, node_color=list(partition.values()), cmap='viridis', node_size=200)
nx.draw_networkx_edges(G, pos, alpha=0.5)
plt.title('Gráfico de Rede com Detecção de Comunidades')
plt.show()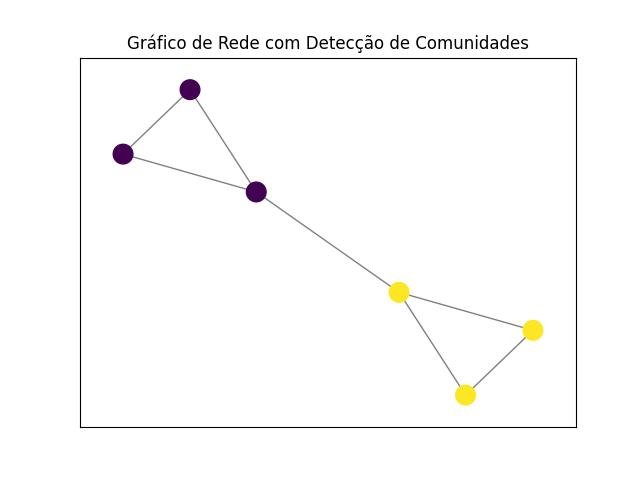
A detecção de comunidades pode fornecer insights valiosos sobre os padrões de interconexão e agrupamentos no seu conjunto de dados.
Lembre-se de adaptar o código de acordo com a estrutura e os dados do seu grafo específico.
Além disso, você pode explorar outros algoritmos de detecção de comunidades e técnicas de visualização disponíveis no NetworkX para obter ainda mais insights sobre seus dados.
Ao longo deste capítulo, você aprenderá não apenas a criar gráficos e visualizações avançadas, mas também a interpretá-los corretamente.
Discutiremos boas práticas na escolha de gráficos apropriados para diferentes tipos de dados e objetivos analíticos.
Além disso, abordaremos técnicas de design visual que melhoram a clareza e a eficácia das visualizações, garantindo que as mensagens sejam transmitidas de forma precisa e impactante.
Através da exploração das técnicas de gráficos e visualizações avançadas, você estará equipado com ferramentas poderosas para desvendar insights valiosos e comunicar efetivamente suas descobertas.
Essas habilidades são essenciais para a análise exploratória de dados, permitindo que você aproveite todo o potencial informativo dos dados e tome decisões embasadas em evidências.
2.1.2.6 - Mapa polar
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.patches import FancyArrowPatch
from mpl_toolkits.mplot3d import proj3d
class Arrow3D(FancyArrowPatch):
def __init__(self, xs, ys, zs, *args, **kwargs):
super().__init__((0,0), (0,0), *args, **kwargs)
self._verts3d = xs, ys, zs
def do_3d_projection(self, renderer=None):
xs3d, ys3d, zs3d = self._verts3d
xs, ys, zs = proj3d.proj_transform(xs3d, ys3d, zs3d, self.axes.M)
self.set_positions((xs[0],ys[0]),(xs[1],ys[1]))
return np.min(zs)
# mpl < 3.5
# class Arrow3D(FancyArrowPatch):
# def __init__(self, xs, ys, zs, *args, **kwargs):
# FancyArrowPatch.__init__(self, (0,0), (0,0), *args, **kwargs)
# self._verts3d = xs, ys, zs
#
# def draw(self, renderer):
# xs3d, ys3d, zs3d = self._verts3d
# xs, ys, zs = proj3d.proj_transform(xs3d, ys3d, zs3d, renderer.M)
# self.set_positions((xs[0],ys[0]),(xs[1],ys[1]))
# FancyArrowPatch.draw(self, renderer)
def Rx(phi):
return np.array([[1, 0, 0],
[0, np.cos(phi), -np.sin(phi)],
[0, np.sin(phi), np.cos(phi)]])
def Ry(theta):
return np.array([[np.cos(theta), 0, np.sin(theta)],
[0, 1, 0],
[-np.sin(theta), 0, np.cos(theta)]])
def Rz(psi):
return np.array([[np.cos(psi), -np.sin(psi), 0],
[np.sin(psi), np.cos(psi), 0],
[0, 0, 1]])
# define origin
o = np.array([0,0,0])
# define ox0y0z0 axes
x0 = np.array([1,0,0])
y0 = np.array([0,1,0])
z0 = np.array([0,0,1])
# define ox1y1z1 axes
psi = 20 * np.pi / 180
x1 = Rz(psi).dot(x0)
y1 = Rz(psi).dot(y0)
z1 = Rz(psi).dot(z0)
# define ox2y2z2 axes
theta = 10 * np.pi / 180
x2 = Rz(psi).dot(Ry(theta)).dot(x0)
y2 = Rz(psi).dot(Ry(theta)).dot(y0)
z2 = Rz(psi).dot(Ry(theta)).dot(z0)
# define ox3y3z3 axes
phi = 30 * np.pi / 180
x3 = Rz(psi).dot(Ry(theta)).dot(Rx(phi)).dot(x0)
y3 = Rz(psi).dot(Ry(theta)).dot(Rx(phi)).dot(y0)
z3 = Rz(psi).dot(Ry(theta)).dot(Rx(phi)).dot(z0)
# produce figure
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
arrow_prop_dict = dict(mutation_scale=20, arrowstyle='-|>', color='k', shrinkA=0, shrinkB=0)
# plot ox0y0z0 axes
a = Arrow3D([o[0], x0[0]], [o[1], x0[1]], [o[2], x0[2]], **arrow_prop_dict)
ax.add_artist(a)
a = Arrow3D([o[0], y0[0]], [o[1], y0[1]], [o[2], y0[2]], **arrow_prop_dict)
ax.add_artist(a)
a = Arrow3D([o[0], z0[0]], [o[1], z0[1]], [o[2], z0[2]], **arrow_prop_dict)
ax.add_artist(a)
# plot ox1y1z1 axes
a = Arrow3D([o[0], x1[0]], [o[1], x1[1]], [o[2], x1[2]], **arrow_prop_dict)
ax.add_artist(a)
a = Arrow3D([o[0], y1[0]], [o[1], y1[1]], [o[2], y1[2]], **arrow_prop_dict)
ax.add_artist(a)
a = Arrow3D([o[0], z1[0]], [o[1], z1[1]], [o[2], z1[2]], **arrow_prop_dict)
ax.add_artist(a)
# draw dotted arc in x0y0 plane
arc = np.arange(-5,116) * np.pi / 180
p = np.array([np.cos(arc),np.sin(arc),arc * 0])
ax.plot(p[0,:],p[1,:],p[2,:],'k--')
# mark z0 rotation angles (psi)
arc = np.linspace(0,psi)
p = np.array([np.cos(arc),np.sin(arc),arc * 0]) * 0.6
ax.plot(p[0,:],p[1,:],p[2,:],'k')
p = np.array([-np.sin(arc),np.cos(arc),arc * 0]) * 0.6
ax.plot(p[0,:],p[1,:],p[2,:],'k')
# plot ox2y2z2 axes
a = Arrow3D([o[0], x2[0]], [o[1], x2[1]], [o[2], x2[2]], **arrow_prop_dict)
ax.add_artist(a)
a = Arrow3D([o[0], y2[0]], [o[1], y2[1]], [o[2], y2[2]], **arrow_prop_dict)
ax.add_artist(a)
a = Arrow3D([o[0], z2[0]], [o[1], z2[1]], [o[2], z2[2]], **arrow_prop_dict)
ax.add_artist(a)
# draw dotted arc in x1z1 plane
arc = np.arange(-5,105) * np.pi / 180
p = np.array([np.sin(arc),arc * 0,np.cos(arc)])
p = Rz(psi).dot(p)
ax.plot(p[0,:],p[1,:],p[2,:],'k--')
# mark y1 rotation angles (theta)
arc = np.linspace(0,theta)
p = np.array([np.cos(arc),arc * 0,-np.sin(arc)]) * 0.6
p = Rz(psi).dot(p)
ax.plot(p[0,:],p[1,:],p[2,:],'k')
p = np.array([np.sin(arc),arc * 0,np.cos(arc)]) * 0.6
p = Rz(psi).dot(p)
ax.plot(p[0,:],p[1,:],p[2,:],'k')
# plot ox3y3z3 axes
a = Arrow3D([o[0], x3[0]], [o[1], x3[1]], [o[2], x3[2]], **arrow_prop_dict)
ax.add_artist(a)
a = Arrow3D([o[0], y3[0]], [o[1], y3[1]], [o[2], y3[2]], **arrow_prop_dict)
ax.add_artist(a)
a = Arrow3D([o[0], z3[0]], [o[1], z3[1]], [o[2], z3[2]], **arrow_prop_dict)
ax.add_artist(a)
# draw dotted arc in y2z2 plane
arc = np.arange(-5,125) * np.pi / 180
p = np.array([arc * 0,np.cos(arc),np.sin(arc)])
p = Rz(psi).dot(Ry(theta)).dot(p)
ax.plot(p[0,:],p[1,:],p[2,:],'k--')
# mark x2 rotation angles (phi)
arc = np.linspace(0,phi)
p = np.array([arc * 0,np.cos(arc),np.sin(arc)]) * 0.6
p = Rz(psi).dot(Ry(theta)).dot(p)
ax.plot(p[0,:],p[1,:],p[2,:],'k')
p = np.array([arc * 0,-np.sin(arc),np.cos(arc)]) * 0.6
p = Rz(psi).dot(Ry(theta)).dot(p)
ax.plot(p[0,:],p[1,:],p[2,:],'k')
text_options = {'horizontalalignment': 'center',
'verticalalignment': 'center',
'fontsize': 14}
# add label for origin
ax.text(0.0,0.0,-0.05,r'$o$', **text_options)
# add labels for x axes
ax.text(1.1*x0[0],1.1*x0[1],1.1*x0[2],r'$x_0$', **text_options)
ax.text(1.1*x1[0],1.1*x1[1],1.1*x1[2],r'$x_1$', **text_options)
ax.text(1.1*x2[0],1.1*x2[1],1.1*x2[2],r'$x_2, x_3$', **text_options)
# add lables for y axes
ax.text(1.1*y0[0],1.1*y0[1],1.1*y0[2],r'$y_0$', **text_options)
ax.text(1.1*y1[0],1.1*y1[1],1.1*y1[2],r'$y_1, y_2$', **text_options)
ax.text(1.1*y3[0],1.1*y3[1],1.1*y3[2],r'$y_3$', **text_options)
# add lables for z axes
ax.text(1.1*z0[0],1.1*z0[1],1.1*z0[2],r'$z_0, z_1$', **text_options)
ax.text(1.1*z2[0],1.1*z2[1],1.1*z2[2],r'$z_2$', **text_options)
ax.text(1.1*z3[0],1.1*z3[1],1.1*z3[2],r'$z_3$', **text_options)
# add psi angle labels
m = 0.55 * ((x0 + x1) / 2.0)
ax.text(m[0], m[1], m[2], r'$\psi$', **text_options)
m = 0.55 * ((y0 + y1) / 2.0)
ax.text(m[0], m[1], m[2], r'$\psi$', **text_options)
# add theta angle lables
m = 0.55 * ((x1 + x2) / 2.0)
ax.text(m[0], m[1], m[2], r'$\theta$', **text_options)
m = 0.55 * ((z1 + z2) / 2.0)
ax.text(m[0], m[1], m[2], r'$\theta$', **text_options)
# add phi angle lables
m = 0.55 * ((y2 + y3) / 2.0)
ax.text(m[0], m[1], m[2], r'$\phi$', **text_options)
m = 0.55 * ((z2 + z3) / 2.0)
ax.text(m[0], m[1], m[2], r'$\phi$', **text_options)
# show figure
ax.view_init(elev=-150, azim=60)
ax.set_axis_off()
plt.show()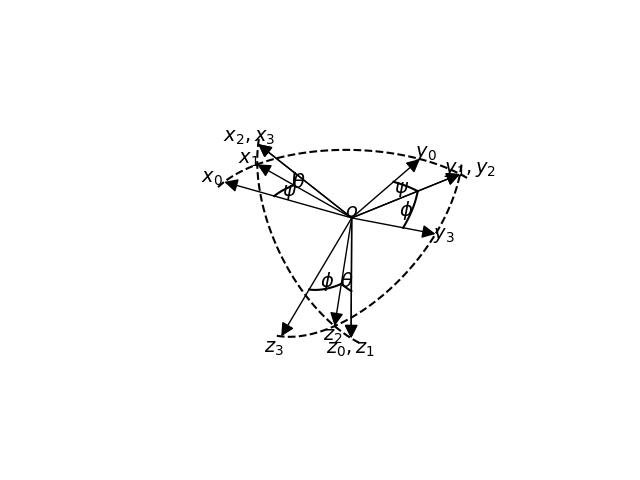
2.1.3 - Galeria Matplotlib
2.1.3.1 - Gráficos 3d
2.1.3.1.1 - Gráfico de dispersão 3D
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
from matplotlib import pyplot as plt
# Gere alguns dados de amostra 3D
mu_vec1 = np.array([0,0,0]) # mean vector
cov_mat1 = np.array([[1,0,0],[0,1,0],[0,0,1]]) # covariance matrix
class1_sample = np.random.multivariate_normal(mu_vec1, cov_mat1, 20)
class2_sample = np.random.multivariate_normal(mu_vec1 + 1, cov_mat1, 20)
class3_sample = np.random.multivariate_normal(mu_vec1 + 2, cov_mat1, 20)
# class1_sample.shape -> (20, 3), 20 linhas, 3 colunas
fig = plt.figure(figsize=(8,8))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(
class1_sample[:,0], class1_sample[:,1], class1_sample[:,2],
marker='x', color='blue', s=40, label='class 1')
ax.scatter(
class2_sample[:,0], class2_sample[:,1], class2_sample[:,2],
marker='o', color='green', s=40, label='class 2')
ax.scatter(
class3_sample[:,0], class3_sample[:,1], class3_sample[:,2],
marker='^', color='red', s=40, label='class 3')
ax.set_xlabel('variable X')
ax.set_ylabel('variable Y')
ax.set_zlabel('variable Z')
plt.title('Gráfico de dispersão 3D')
plt.show()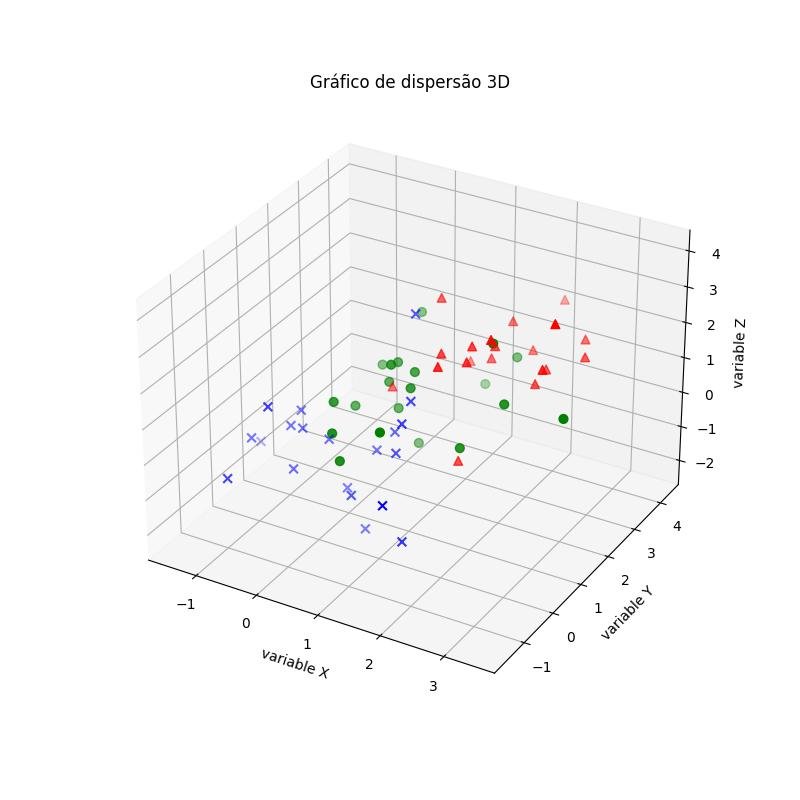
2.1.3.1.2 - Gráfico de dispersão 3D com autovetores
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.patches import FancyArrowPatch
from mpl_toolkits.mplot3d import proj3d
class Arrow3D(FancyArrowPatch):
def __init__(self, xs, ys, zs, *args, **kwargs):
FancyArrowPatch.__init__(self, (0,0), (0,0), *args, **kwargs)
self._verts3d = xs, ys, zs
def do_3d_projection(self, renderer=None):
xs3d, ys3d, zs3d = self._verts3d
xs, ys, zs = proj3d.proj_transform(xs3d, ys3d, zs3d, self.axes.M)
self.set_positions((xs[0],ys[0]),(xs[1],ys[1]))
return np.min(zs)
# Gerar alguns dados de exemplo
mu_vec1 = np.array([0,0,0])
cov_mat1 = np.array([[1,0,0],[0,1,0],[0,0,1]])
class1_sample = np.random.multivariate_normal(mu_vec1, cov_mat1, 20)
mu_vec2 = np.array([1,1,1])
cov_mat2 = np.array([[1,0,0],[0,1,0],[0,0,1]])
class2_sample = np.random.multivariate_normal(mu_vec2, cov_mat2, 20)
# concatenar dados para PCA
amostras = np.concatenate((class1_sample, class2_sample), axis=0)
# valores médios
mean_x = np.mean(amostras[:,0])
mean_y = np.mean(amostras[:,1])
mean_z = np.mean(amostras[:,2])
# autovetores e autovalores
eig_val, eig_vec = np.linalg.eig(cov_mat1)
################################
# plotagem de autovetores
#################################
fig = plt.figure(figsize=(10,10))
ax = fig.add_subplot(111, projection='3d')
ax.plot(amostras[:,0], amostras[:,1], amostras[:,2], 'o', markersize=10, color='green', alpha=0.2)
ax.plot([mean_x], [mean_y], [mean_z], 'o', markersize=10, color='red', alpha=0.5)
for v in eig_vec.T:
a = Arrow3D([mean_x, v[0]], [mean_y, v[1]],
[mean_z, v[2]], mutation_scale=20, lw=3, arrowstyle="-|>", color="r")
ax.add_artist(a)
ax.set_xlabel('variable X')
ax.set_ylabel('variable Y')
ax.set_zlabel('variable Z')
plt.title('Gráfico de dispersão 3D com autovetores')
plt.show()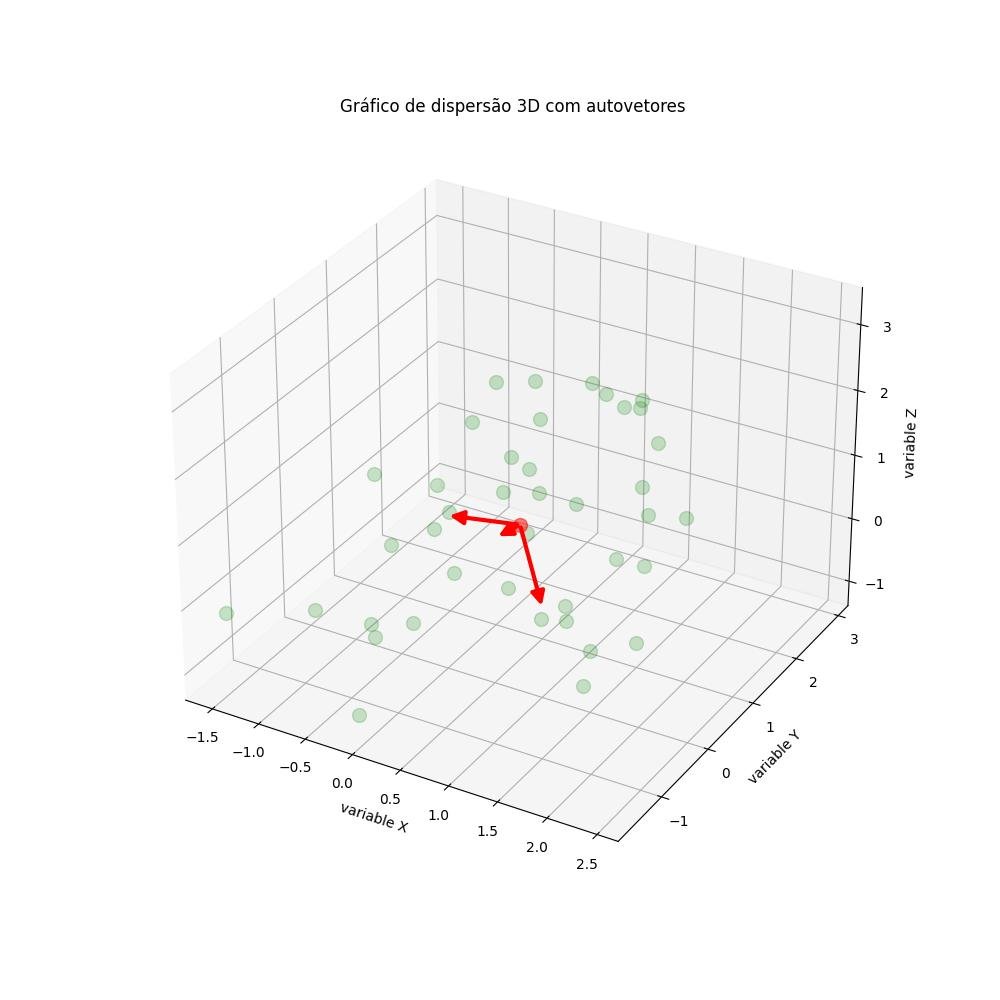
2.1.3.1.3 - Cubo 3D
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
from itertools import product, combinations
fig = plt.figure(figsize=(7,7))
ax = fig.gca(projection='3d')
ax.set_aspect("auto")
# Pontos de plotagem
# Amostras dentro do cubo
X_inside = np.array([[0,0,0],[0.2,0.2,0.2],[0.1, -0.1, -0.3]])
X_outside = np.array([[-1.2,0.3,-0.3],[0.8,-0.82,-0.9],[1, 0.6, -0.7],
[0.8,0.7,0.2],[0.7,-0.8,-0.45],[-0.3, 0.6, 0.9],
[0.7,-0.6,-0.8]])
for row in X_inside:
ax.scatter(row[0], row[1], row[2], color="r", s=50, marker='^')
for row in X_outside:
ax.scatter(row[0], row[1], row[2], color="k", s=50)
# Cubo de plotagem
h = [-0.5, 0.5]
for s, e in combinations(np.array(list(product(h,h,h))), 2):
if np.sum(np.abs(s-e)) == h[1]-h[0]:
ax.plot3D(*zip(s,e), color="g")
ax.set_xlim(-1.5, 1.5)
ax.set_ylim(-1.5, 1.5)
ax.set_zlim(-1.5, 1.5)
plt.show()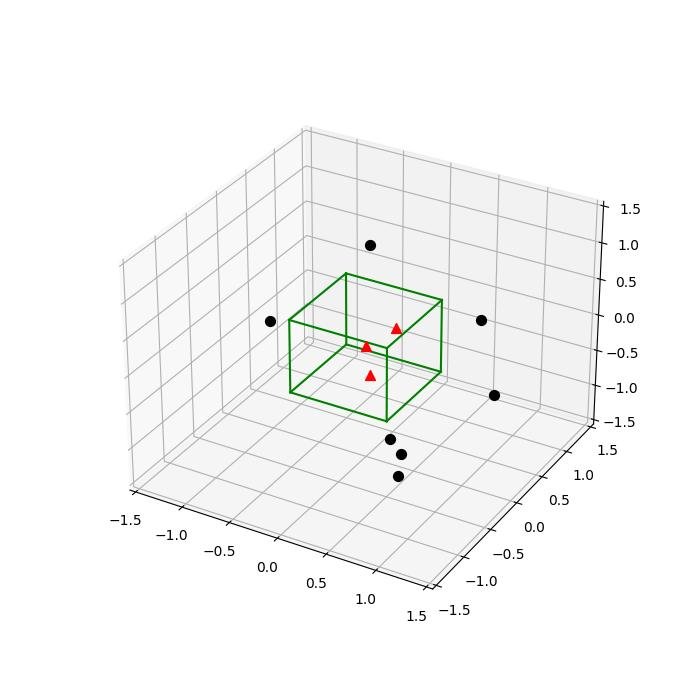
2.1.3.1.4 - Distribuição gaussiana multivariada com superfície colorida
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def bivariate_normal(X, Y, sigmax=1.0, sigmay=1.0, mux=0.0, muy=0.0, sigmaxy=0.0):
"""
Distribuição gaussiana bivariada para formas iguais *X*, *Y*.
Veja em mathworld: <a href='http://mathworld.wolfram.com/BivariateNormalDistribution.html'>bivariate normal distribution</a>.
"""
Xmu = X-mux
Ymu = Y-muy
rho = sigmaxy/(sigmax*sigmay)
z = Xmu**2/sigmax**2 + Ymu**2/sigmay**2 - 2*rho*Xmu*Ymu/(sigmax*sigmay)
denom = 2*np.pi*sigmax*sigmay*np.sqrt(1-rho**2)
return np.exp(-z/(2*(1-rho**2))) / denom
fig = plt.figure(figsize=(10, 7))
ax = fig.gca(projection='3d')
x = np.linspace(-5, 5, 200)
y = x
X,Y = np.meshgrid(x, y)
Z = bivariate_normal(X, Y)
surf = ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=plt.cm.coolwarm,
linewidth=0, antialiased=False)
ax.set_zlim(0, 0.2)
ax.zaxis.set_major_locator(plt.LinearLocator(10))
ax.zaxis.set_major_formatter(plt.FormatStrFormatter('%.02f'))
fig.colorbar(surf, shrink=0.5, aspect=7, cmap=plt.cm.coolwarm)
plt.show()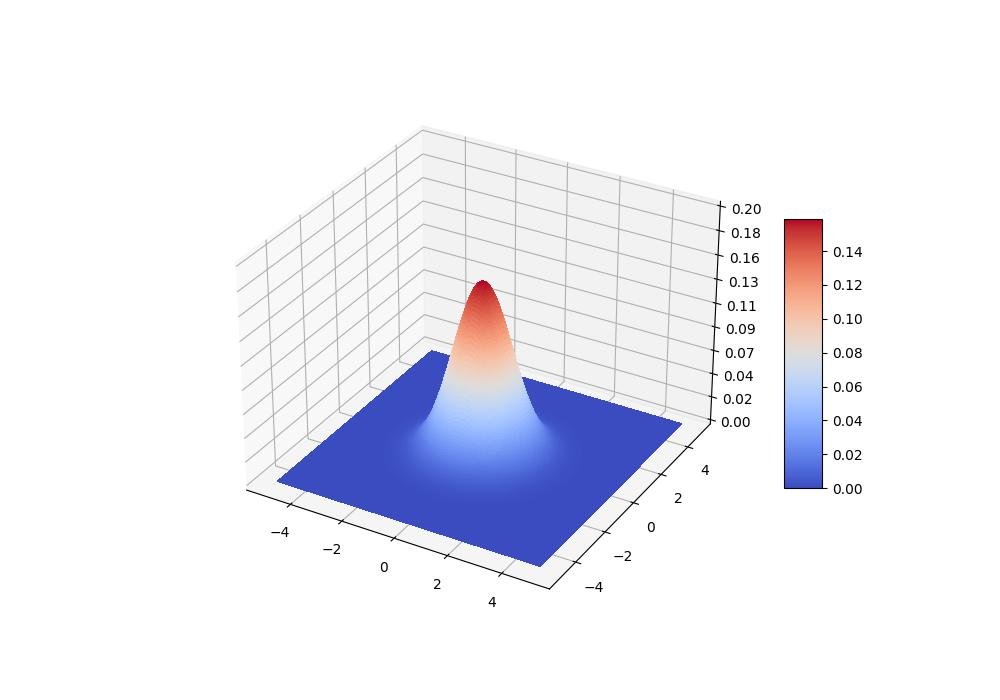
2.1.3.1.5 - Distribuição gaussiana multivariada como grade de malha
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(10, 7))
ax = fig.gca(projection='3d')
x = np.linspace(-5, 5, 200)
y = x
X,Y = np.meshgrid(x, y)
Z = bivariate_normal(X, Y)
surf = ax.plot_wireframe(X, Y, Z, rstride=4, cstride=4, color='g', alpha=0.7)
ax.set_zlim(0, 0.2)
ax.zaxis.set_major_locator(plt.LinearLocator(10))
ax.zaxis.set_major_formatter(plt.FormatStrFormatter('%.02f'))
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('p(x)')
plt.title('Gaussiano bivariado')
plt.show()
2.1.3.2 - Gráficos de barras
2.1.3.2.1 - Gráfico de barras com barras de erro
import matplotlib.pyplot as plt
# Dados de entrada
mean_values = [1, 2, 3]
variance = [0.2, 0.4, 0.5]
bar_labels = ['bar 1', 'bar 2', 'bar 3']
# barras de plotagem
x_pos = list(range(len(bar_labels)))
plt.bar(x_pos, mean_values, yerr=variance, align='center', alpha=0.5)
plt.grid()
# definir a altura do eixo y
max_y = max(zip(mean_values, variance)) # returns a tuple, here: (3, 5)
plt.ylim([0, (max_y[0] + max_y[1]) * 1.1])
# definir rótulos de eixos e título
plt.ylabel('variável y')
plt.xticks(x_pos, bar_labels)
plt.title('Gráfico de barras com barras de erro')
plt.show()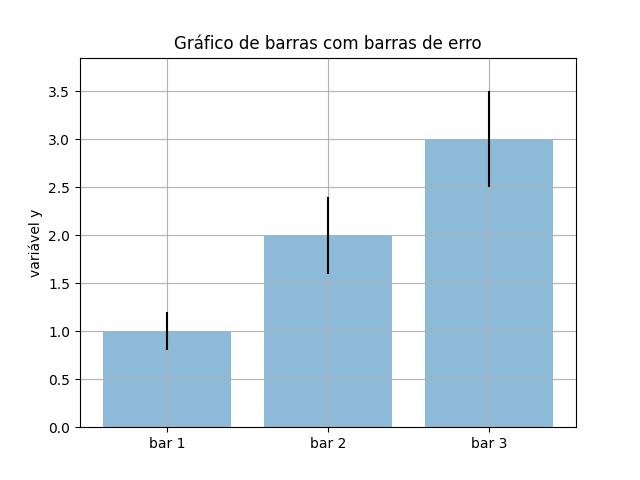
2.1.3.2.2 - Gráfico de barra horizontal com barras de erro
from matplotlib import pyplot as plt
import numpy as np
# Dados de entrada
mean_values = [1, 2, 3]
std_dev = [0.2, 0.4, 0.5]
bar_labels = ['bar 1', 'bar 2', 'bar 3']
fig = plt.figure(figsize=(8,6))
# barras de plotagem
y_pos = np.arange(len(mean_values))
y_pos = [x for x in y_pos]
plt.yticks(y_pos, bar_labels, fontsize=10)
plt.barh(y_pos, mean_values, xerr=std_dev,
align='center', alpha=0.4, color='g')
# anotação e rótulos
plt.xlabel('medida x')
t = plt.title('Gráfico de barras com desvio padrão')
plt.ylim([-1,len(mean_values)+0.5])
plt.xlim([0, 4])
plt.grid()
plt.show()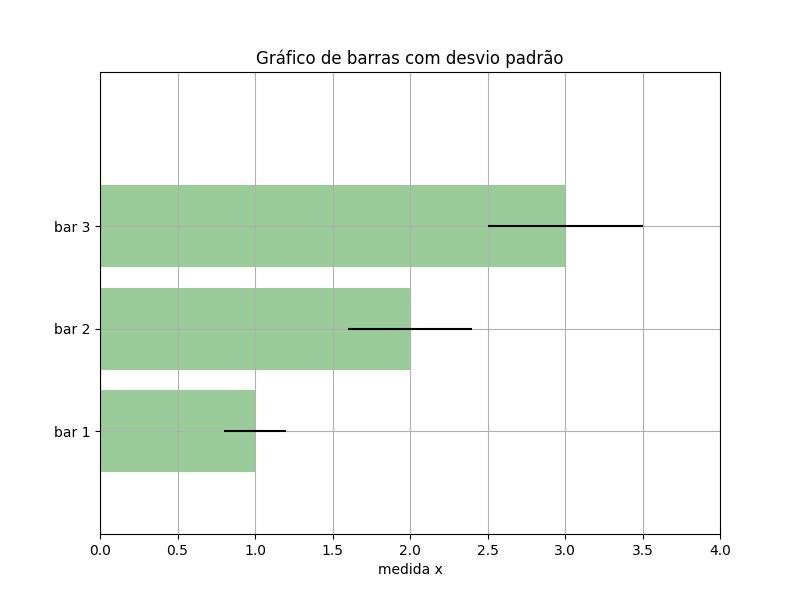
2.1.3.2.3 - Gráfico de barra back-to-back
from matplotlib import pyplot as plt
import numpy as np
# Dados de entrada
X1 = np.array([1, 2, 3])
X2 = np.array([2, 2, 3])
bar_labels = ['bar 1', 'bar 2', 'bar 3']
fig = plt.figure(figsize=(8,6))
# barras de plotagem
y_pos = np.arange(len(X1))
y_pos = [x for x in y_pos]
plt.yticks(y_pos, bar_labels, fontsize=10)
plt.barh(y_pos, X1,
align='center', alpha=0.4, color='g')
# simplesmente negamos os valores do array numpy para a segunda barra
plt.barh(y_pos, -X2,
align='center', alpha=0.4, color='b')
# anotação e rótulos
plt.xlabel('medida x')
t = plt.title('Gráfico de barras com desvio padrão')
plt.ylim([-1,len(X1)+0.1])
plt.xlim([-max(X2)-1, max(X1)+1])
plt.grid()
plt.show()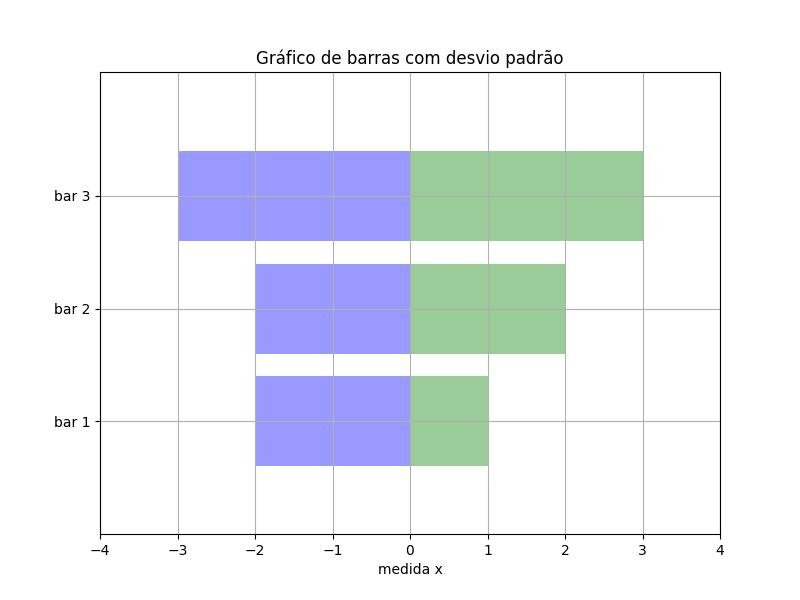
2.1.3.2.4 - gráfico de barras agrupadas
import matplotlib.pyplot as plt
# Dados de entrada
green_data = [1, 2, 3]
blue_data = [3, 2, 1]
red_data = [2, 3, 3]
labels = ['group 1', 'group 2', 'group 3']
# Definindo as posições e a largura das barras
pos = list(range(len(green_data)))
width = 0.2
# Plotando as barras
fig, ax = plt.subplots(figsize=(8,6))
plt.bar(pos, green_data, width,
alpha=0.5,
color='g',
label=labels[0])
plt.bar([p + width for p in pos], blue_data, width,
alpha=0.5,
color='b',
label=labels[1])
plt.bar([p + width*2 for p in pos], red_data, width,
alpha=0.5,
color='r',
label=labels[2])
# Configurando rótulos e marcas de eixo
ax.set_ylabel('y-value')
ax.set_title('Grouped bar plot')
ax.set_xticks([p + 1.5 * width for p in pos])
ax.set_xticklabels(labels)
# Definindo os limites do eixo x e do eixo y
plt.xlim(min(pos)-width, max(pos)+width*4)
plt.ylim([0, max(green_data + blue_data + red_data) * 1.5])
# Adicionando a legenda e mostrando o gráfico
plt.legend(['green', 'blue', 'red'], loc='upper left')
plt.grid()
plt.show()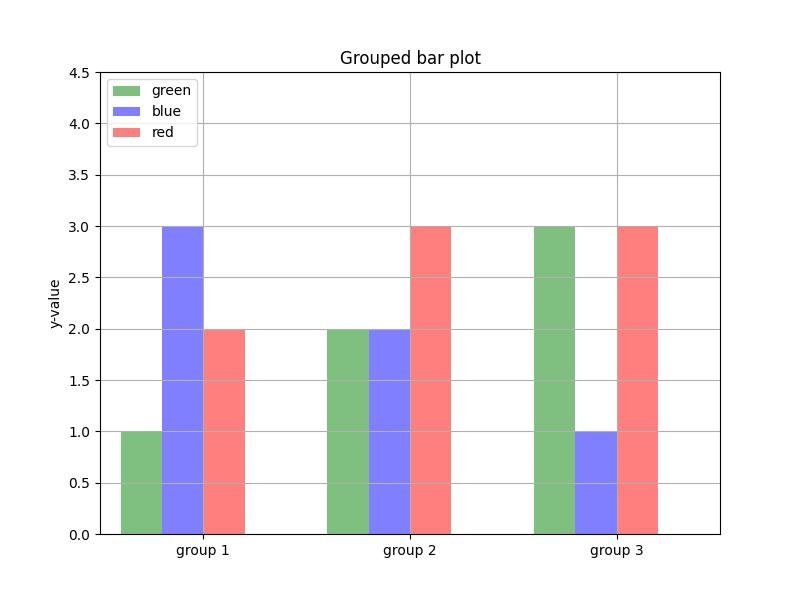
2.1.3.2.5 - Gráfico de barras empilhadas
import matplotlib.pyplot as plt
blue_data = [100,120,140]
red_data = [150,120,190]
green_data = [80,70,90]
f, (ax1, ax2) = plt.subplots(1, 2, figsize=(10,5))
bar_width = 0.5
# posições dos limites da barra esquerda
bar_l = [i+1 for i in range(len(blue_data))]
# posições dos ticks do eixo x (centro das barras como rótulos de barras)
tick_pos = [i+(bar_width/2) for i in bar_l]
####################
## contagem absoluta
####################
ax1.bar(bar_l, blue_data, width=bar_width,
label='blue data', alpha=0.5, color='b')
ax1.bar(bar_l, red_data, width=bar_width,
bottom=blue_data, label='red data', alpha=0.5, color='r')
ax1.bar(bar_l, green_data, width=bar_width,
bottom=[i+j for i,j in zip(blue_data,red_data)], label='green data', alpha=0.5, color='g')
plt.sca(ax1)
plt.xticks(tick_pos, ['category 1', 'category 2', 'category 3'])
ax1.set_ylabel("Count")
ax1.set_xlabel("")
plt.legend(loc='upper left')
plt.xlim([min(tick_pos)-bar_width, max(tick_pos)+bar_width])
plt.grid()
# girar rótulos de eixo
plt.setp(plt.gca().get_xticklabels(), rotation=45, horizontalalignment='right')
#############
## Percentual
#############
totals = [i+j+k for i,j,k in zip(blue_data, red_data, green_data)]
blue_rel = [i / j * 100 for i,j in zip(blue_data, totals)]
red_rel = [i / j * 100 for i,j in zip(red_data, totals)]
green_rel = [i / j * 100 for i,j in zip(green_data, totals)]
ax2.bar(bar_l, blue_rel,
label='blue data', alpha=0.5, color='b', width=bar_width
)
ax2.bar(bar_l, red_rel,
bottom=blue_rel, label='red data', alpha=0.5, color='r', width=bar_width
)
ax2.bar(bar_l, green_rel,
bottom=[i+j for i,j in zip(blue_rel, red_rel)],
label='green data', alpha=0.5, color='g', width=bar_width
)
plt.sca(ax2)
plt.xticks(tick_pos, ['category 1', 'category 2', 'category 3'])
ax2.set_ylabel("Percentage")
ax2.set_xlabel("")
plt.xlim([min(tick_pos)-bar_width, max(tick_pos)+bar_width])
plt.grid()
# girar rótulos de eixo
plt.setp(plt.gca().get_xticklabels(), rotation=45, horizontalalignment='right')
plt.show()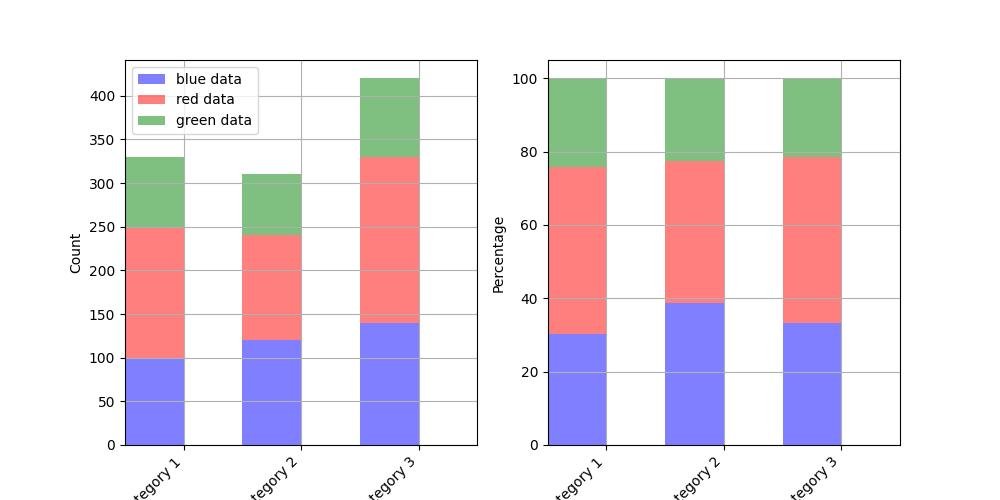
2.1.3.2.6 - Gráfico de barras com rótulos de gráfico/texto 1
from matplotlib import pyplot as plt
import numpy as np
data = range(200, 225, 5)
bar_labels = ['a', 'b', 'c', 'd', 'e']
fig = plt.figure(figsize=(10,8))
# barras de plotagem
y_pos = np.arange(len(data))
plt.yticks(y_pos, bar_labels, fontsize=16)
bars = plt.barh(y_pos, data,
align='center', alpha=0.4, color='g')
# anotação e rótulos
for b,d in zip(bars, data):
plt.text(b.get_width() + b.get_width()*0.08, b.get_y() + b.get_height()/2,
'{0:.2%}'.format(d/min(data)),
ha='center', va='bottom', fontsize=12)
plt.xlabel('X axis label', fontsize=14)
plt.ylabel('Y axis label', fontsize=14)
t = plt.title('Gráfico de barras com rótulos/texto do gráfico', fontsize=18)
plt.ylim([-1,len(data)+0.5])
plt.vlines(min(data), -1, len(data)+0.5, linestyles='dashed')
plt.grid()
plt.show()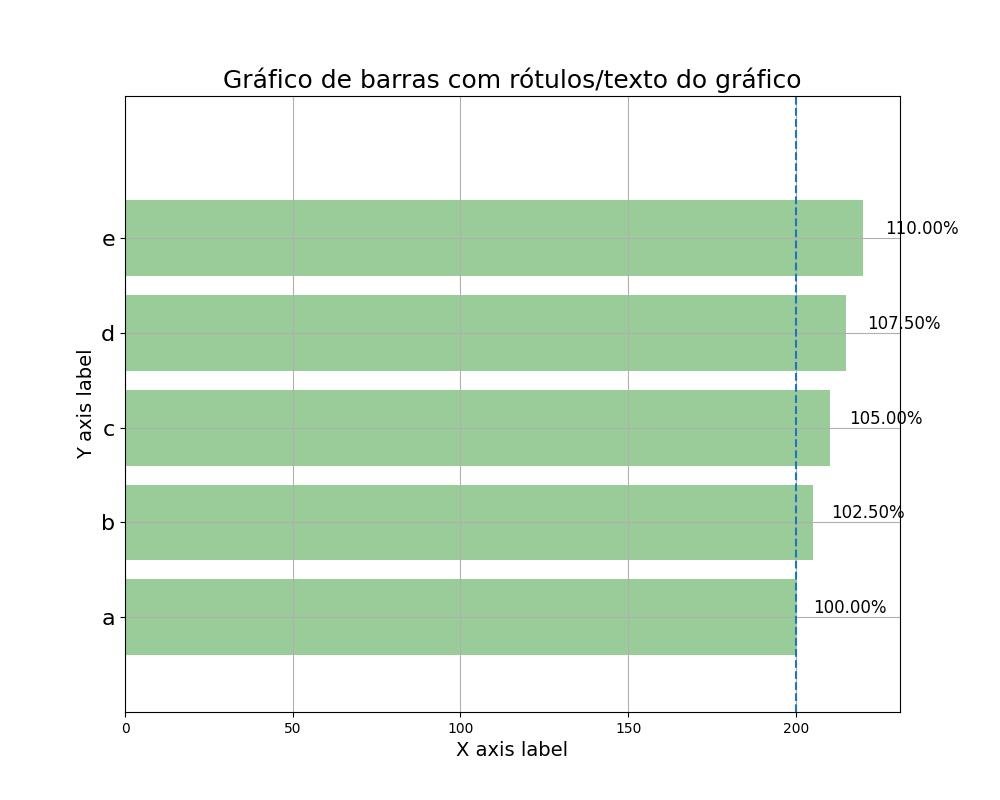
2.1.3.2.7 - Gráfico de barras com rótulos de gráfico/texto 2
import matplotlib.pyplot as plt
# Dados de entrada
mean_values = [1, 2, 3]
bar_labels = ['bar 1', 'bar 2', 'bar 3']
# barras de plotagem
x_pos = list(range(len(bar_labels)))
rects = plt.bar(x_pos, mean_values, align='center', alpha=0.5)
# barras de rótulo
def autolabel(rects):
for ii,rect in enumerate(rects):
height = rect.get_height()
plt.text(rect.get_x()+rect.get_width()/2., 1.02*height, '%s'% (mean_values[ii]),
ha='center', va='bottom')
autolabel(rects)
# definir a altura do eixo y
max_y = max(zip(mean_values, variance)) # returns a tuple, here: (3, 5)
plt.ylim([0, (max_y[0] + max_y[1]) * 1.1])
# definir rótulos de eixos e título
plt.ylabel('variável y')
plt.xticks(x_pos, bar_labels)
plt.title('Gráfico de barras com rótulos')
plt.show()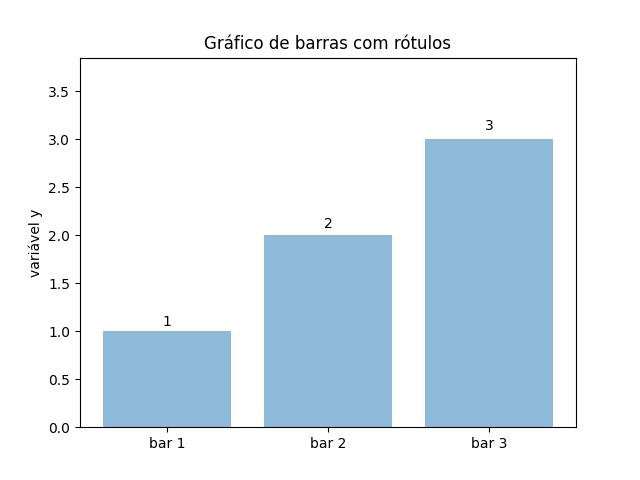
2.1.3.2.8 - Barplot com rótulos e texto com rotação automática
import matplotlib.pyplot as plt
idx = range(4)
values = [100, 1000, 5000, 20000]
labels = ['category 1', 'category 2',
'category 3', 'category 4']
fig, ax = plt.subplots(1)
# Alinhar e girar rótulos de escala automaticamente
fig.autofmt_xdate()
bars = plt.bar(idx, values, align='center')
plt.xticks(idx, labels)
plt.tight_layout()
# Adicione rótulos de texto ao topo das barras
def autolabel(bars):
for bar in bars:
height = bar.get_height()
ax.text(bar.get_x() + bar.get_width()/2., 1.05 * height,
'%d' % int(height),
ha='center', va='bottom')
autolabel(bars)
plt.ylim([0, 25000])
plt.show()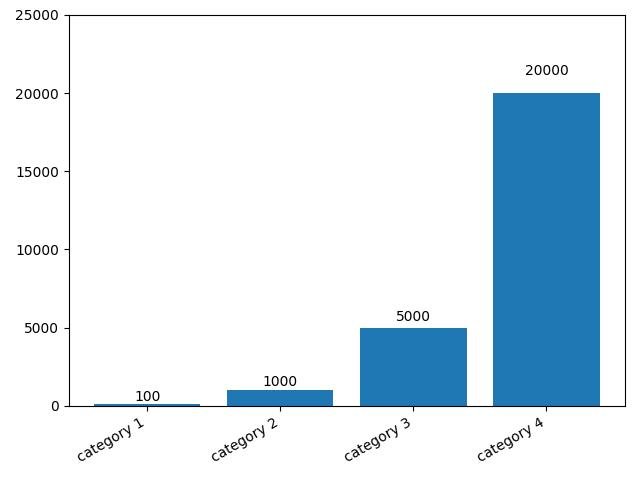
2.1.3.2.9 - Bar plot with color gradients
import matplotlib.pyplot as plt
import matplotlib.colors as col
import matplotlib.cm as cm
# Dados de entrada
mean_values = range(10,18)
x_pos = range(len(mean_values))
# Criar o mapa de cores
cmap1 = cm.ScalarMappable(col.Normalize(min(mean_values), max(mean_values), cm.hot))
cmap2 = cm.ScalarMappable(col.Normalize(0, 20, cm.hot))
# Barras de plotagem
plt.subplot(121)
plt.bar(x_pos, mean_values, align='center', alpha=0.5, color=cmap1.to_rgba(mean_values))
plt.ylim(0, max(mean_values) * 1.1)
plt.subplot(122)
plt.bar(x_pos, mean_values, align='center', alpha=0.5, color=cmap2.to_rgba(mean_values))
plt.ylim(0, max(mean_values) * 1.1)
plt.show()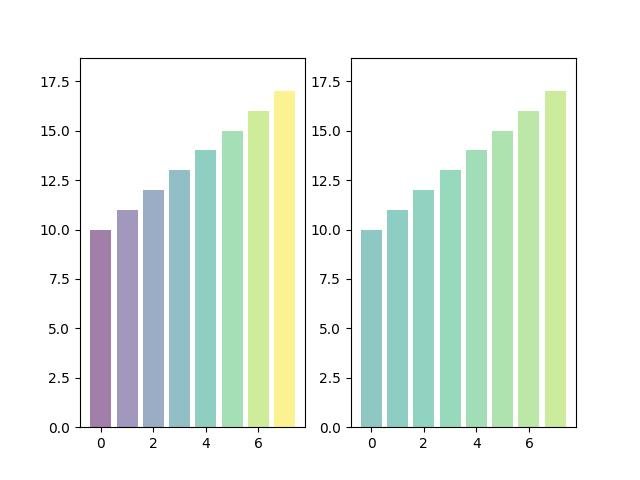
2.1.3.2.10 - Preenchimento de padrão de plotagem de barras
import matplotlib.pyplot as plt
patterns = ('-', '+', 'x', '\\', '*', 'o', 'O', '.')
fig = plt.gca()
# Dados de entrada
mean_values = range(1, len(patterns)+1)
# barras de plotagem
x_pos = list(range(len(mean_values)))
bars = plt.bar(x_pos,
mean_values,
align='center',
color='white',
)
# definir padrões
for bar, pattern in zip(bars, patterns):
bar.set_hatch(pattern)
# definir rótulos de eixos e formatação
fig.axes.get_yaxis().set_visible(False)
plt.ylim([0, max(mean_values) * 1.1])
plt.xticks(x_pos, patterns)
plt.show()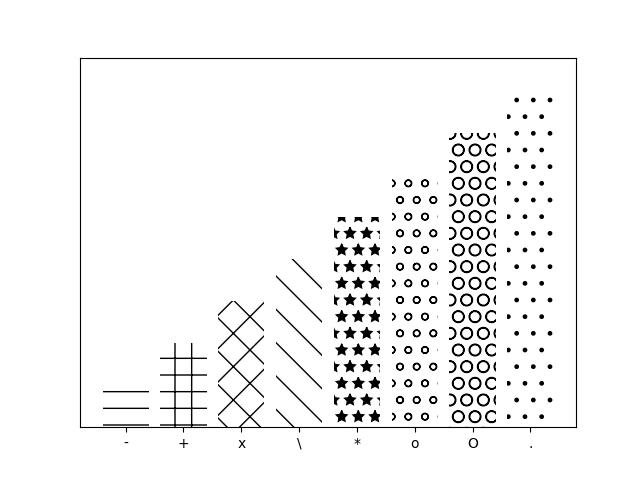
2.1.3.3 - Gráficos de caixa (boxplot)
2.1.3.3.1 - Caixa simples
import matplotlib.pyplot as plt
import numpy as np
all_data = [np.random.normal(0, std, 100) for std in range(1, 4)]
fig = plt.figure(figsize=(8,6))
plt.boxplot(all_data,
notch=False, # box instead of notch shape
sym='rs', # red squares for outliers
vert=True) # vertical box aligmnent
plt.xticks([y+1 for y in range(len(all_data))], ['x1', 'x2', 'x3'])
plt.xlabel('medida x')
t = plt.title('Gráfico de caixa')
plt.show()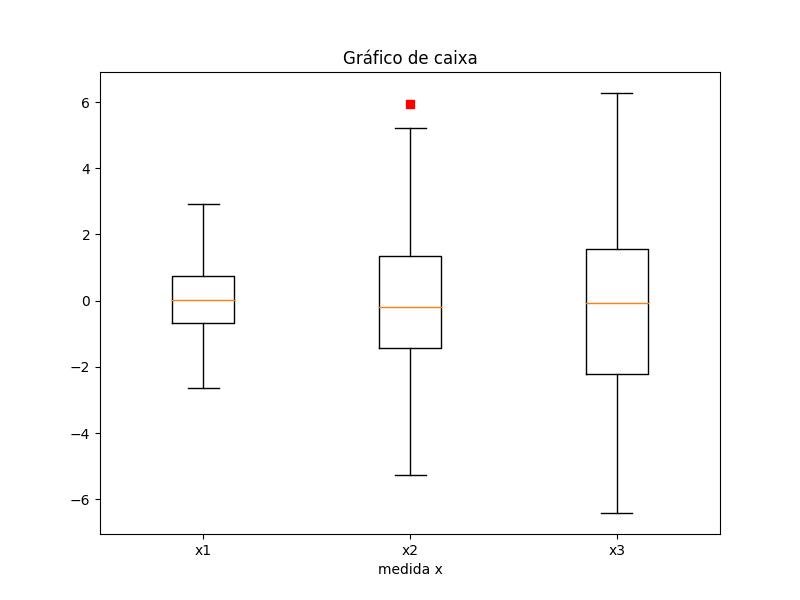
2.1.3.3.2 - Caixas preta e branca
import matplotlib.pyplot as plt
import numpy as np
all_data = [np.random.normal(0, std, 100) for std in range(1, 4)]
fig = plt.figure(figsize=(8,6))
bplot = plt.boxplot(
all_data,
notch=False, # caixa em vez de forma de entalhe
sym='rs', # quadrados vermelhos para outliers
vert=True) # alinhamento vertical da caixa
plt.xticks([y+1 for y in range(len(all_data))], ['x1', 'x2', 'x3'])
plt.xlabel('medida x')
for components in bplot.keys():
for line in bplot[components]:
line.set_color('black') # black lines
t = plt.title('Gráfico de caixa preto e branco')
plt.show()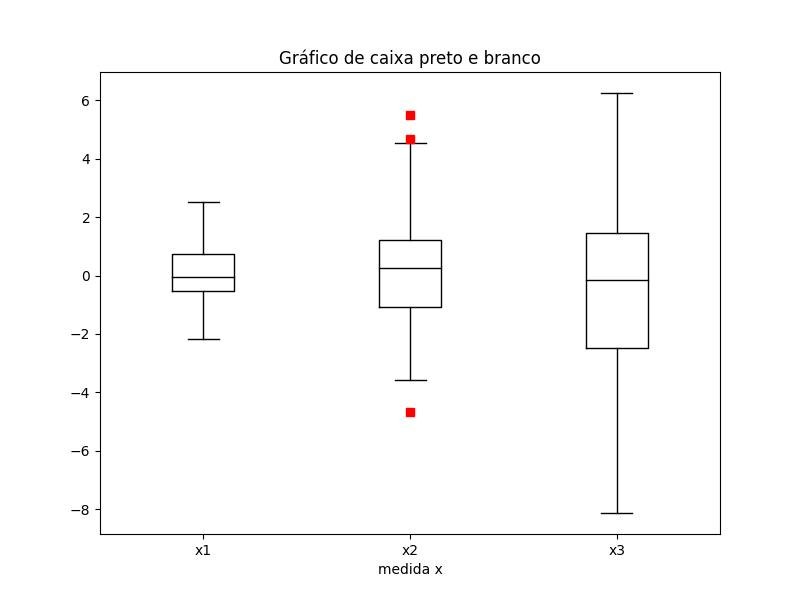
2.1.3.3.3 - Caixa horizontal
import matplotlib.pyplot as plt
import numpy as np
all_data = [np.random.normal(0, std, 100) for std in range(1, 4)]
fig = plt.figure(figsize=(8,6))
plt.boxplot(
all_data,
notch=False, # caixa em vez de forma de entalhe
sym='rs', # quadrados vermelhos para outliers
vert=False) # alinhamento de caixa horizontal
plt.yticks([y+1 for y in range(len(all_data))], ['x1', 'x2', 'x3'])
plt.ylabel('medida x')
t = plt.title('Gráfico de caixa horizontal')
plt.show()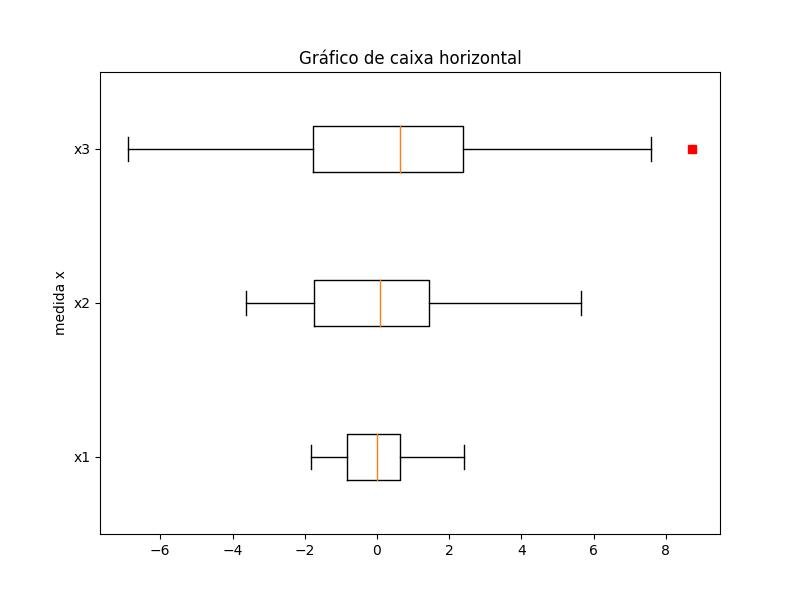
2.1.3.3.4 - Caixa cheia e cilíndrica
import matplotlib.pyplot as plt
import numpy as np
all_data = [np.random.normal(0, std, 100) for std in range(1, 4)]
fig = plt.figure(figsize=(8,6))
plt.boxplot(
all_data,
notch=True, # forma de entalhe
sym='bs', # quadrados azuis para outliers
vert=True, # alinhamento vertical da caixa
patch_artist=True) # preencher com cor
plt.xticks([y+1 for y in range(len(all_data))], ['x1', 'x2', 'x3'])
plt.xlabel('medida x')
t = plt.title('Gráfico de caixa')
plt.show()
2.1.3.3.5 - Boxplots com cores de preenchimento personalizadas
import matplotlib.pyplot as plt
import numpy as np
all_data = [np.random.normal(0, std, 100) for std in range(1, 4)]
fig = plt.figure(figsize=(8,6))
bplot = plt.boxplot(
all_data,
notch=False, # forma de entalhe
vert=True, # alinhamento vertical da caixa
patch_artist=True) # preencher com cor
colors = ['pink', 'lightblue', 'lightgreen']
for patch, color in zip(bplot['boxes'], colors):
patch.set_facecolor(color)
plt.xticks([y+1 for y in range(len(all_data))], ['x1', 'x2', 'x3'])
plt.xlabel('medida x')
t = plt.title('Gráfico de caixa')
plt.show()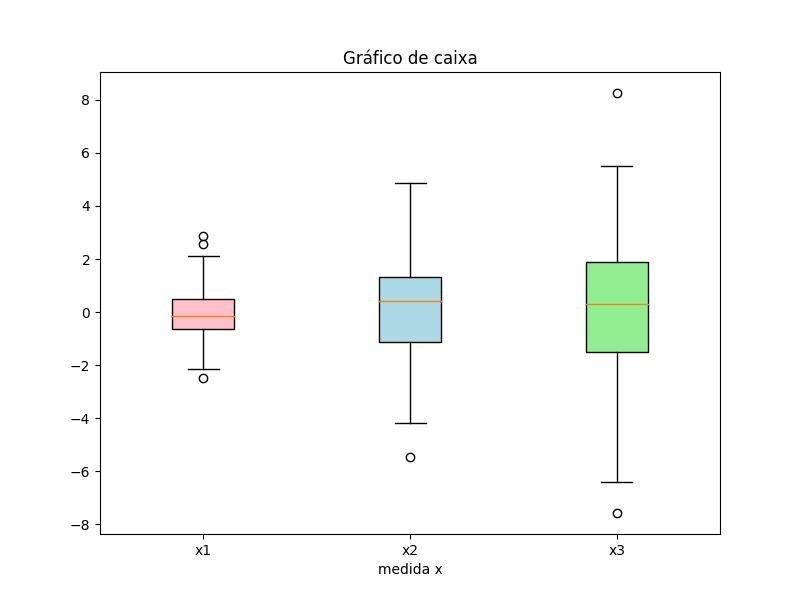
2.1.3.3.6 - Caixa e barras de violino
Os gráficos de violino estão intimamente relacionados aos gráficos de caixa de Tukey (1977), mas adicionam informações úteis, como a distribuição dos dados da amostra (traço de densidade).
import matplotlib.pyplot as plt
import numpy as np
fig, axes = plt.subplots(nrows=1,ncols=2, figsize=(12,5))
all_data = [np.random.normal(0, std, 100) for std in range(6, 10)]
#fig = plt.figure(figsize=(8,6))
axes[0].violinplot(
all_data,
showmeans=False,
showmedians=True
)
axes[0].set_title('violin plot')
axes[1].boxplot(all_data,
)
axes[1].set_title('box plot')
# adicionando linhas de grade horizontais
for ax in axes:
ax.yaxis.grid(True)
ax.set_xticks([y+1 for y in range(len(all_data))], )
ax.set_xlabel('x etiqueta')
ax.set_ylabel('y etiqueta')
plt.setp(
axes, xticks=[y+1 for y in range(len(all_data))],
xticklabels=['x1', 'x2', 'x3', 'x4'],
)
plt.show()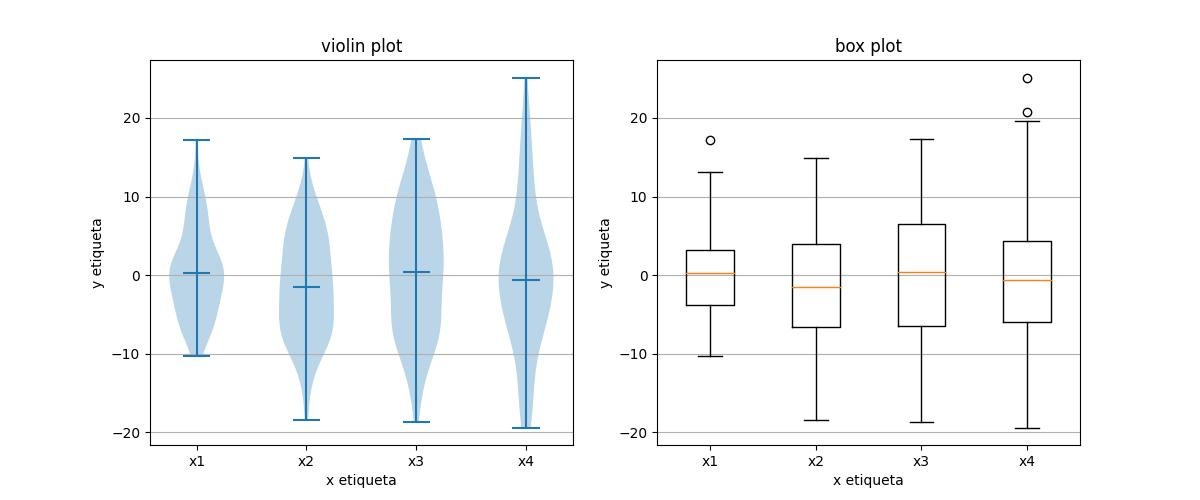
2.1.3.4 - Gráficos de barras de erros
2.1.3.4.1 - Desvio padrão, erro padrão e intervalos de confiança
import numpy as np
from matplotlib import pyplot as plt
from scipy.stats import t
# Gerando 15 pontos de dados aleatórios no intervalo 5-15 (inclusive)
X = np.random.randint(5, 15, 15)
# sample size
n = X.size
# mean
X_mean = np.mean(X)
# desvio padrão
X_std = np.std(X)
# erro padrão
X_se = X_std / np.sqrt(n)
# alternatively:
# from scipy import stats
# stats.sem(X)
# Intervalo de confiança de 95%
dof = n - 1 # graus de liberdade
alpha = 1.0 - 0.95
conf_interval = t.ppf(1-alpha/2., dof) * X_std*np.sqrt(1.+1./n)
fig = plt.gca()
plt.errorbar(1, X_mean, yerr=X_std, fmt='-o')
plt.errorbar(2, X_mean, yerr=X_se, fmt='-o')
plt.errorbar(3, X_mean, yerr=conf_interval, fmt='-o')
plt.xlim([0,4])
plt.ylim(X_mean-conf_interval-2, X_mean+conf_interval+2)
# formatação de eixo
fig.axes.get_xaxis().set_visible(False)
fig.spines["top"].set_visible(False)
fig.spines["right"].set_visible(False)
plt.tick_params(
axis="both", which="both", bottom="off", top="off",
labelbottom="on", left="on", right="off", labelleft="on")
plt.legend(
['Desvio padrão', 'Erro padrão', 'Intervalo de confiança'],
loc='upper left',
numpoints=1,
fancybox=True)
plt.ylabel('variável aleatória')
plt.title('15 valores aleatórios no intervalo 5-15')
plt.show()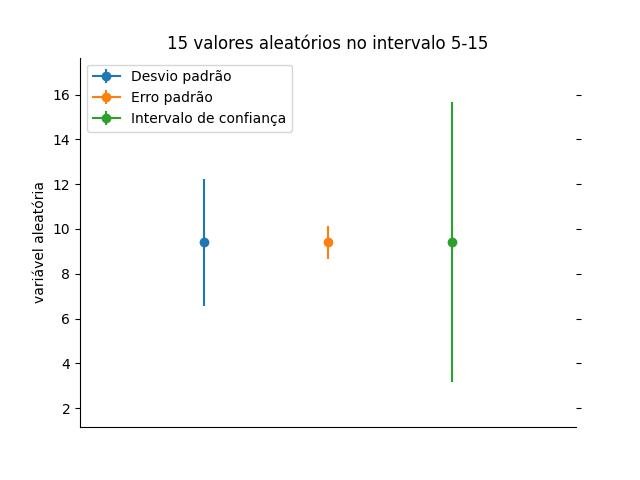
2.1.3.4.2 - Adicionando barras de erro a um barplot
import matplotlib.pyplot as plt
# Dados de entrada
mean_values = [1, 2, 3]
variance = [0.2, 0.4, 0.5]
bar_labels = ['bar 1', 'bar 2', 'bar 3']
fig = plt.gca()
# barras de plotagem
x_pos = list(range(len(bar_labels)))
plt.bar(x_pos, mean_values, yerr=variance, align='center', alpha=0.5)
# definir a altura do eixo y
max_y = max(zip(mean_values, variance)) # returns a tuple, here: (3, 5)
plt.ylim([0, (max_y[0] + max_y[1]) * 1.1])
# definir rótulos de eixos e título
plt.ylabel('variável y')
plt.xticks(x_pos, bar_labels)
plt.title('Gráfico de barras com barras de erro')
# formatação de eixo
fig.axes.get_xaxis().set_visible(False)
fig.spines["top"].set_visible(False)
fig.spines["right"].set_visible(False)
plt.tick_params(
axis="both", which="both", bottom="off", top="off",
labelbottom="on", left="on", right="off", labelleft="on")
plt.show()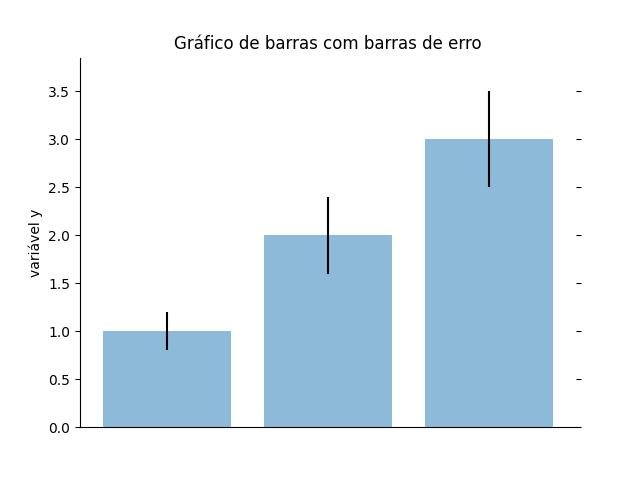
2.1.3.5 - Formatação de gráficos
2.1.3.5.1 - subplots (subtramas)
import numpy as np
import matplotlib.pyplot as plt
x = range(10)
y = range(10)
fig, ax = plt.subplots(2)
for sp in ax: sp.plot(x, y)
plt.show()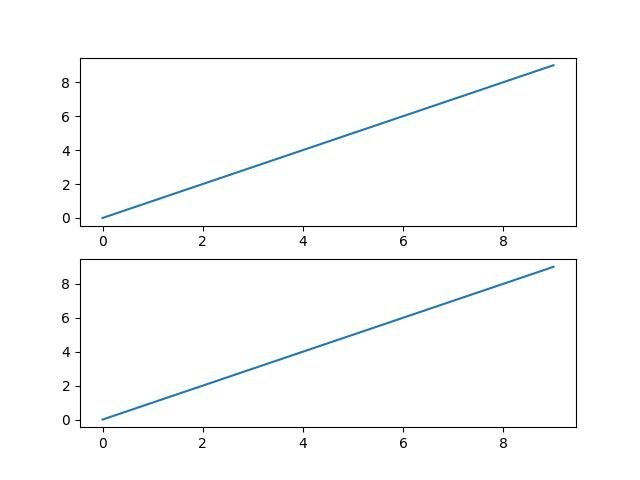
m x n subplots:
import matplotlib.pyplot as plt
x = range(10)
y = range(10)
fig, ax = plt.subplots(nrows=2,ncols=2)
for row in ax:
for col in row:
col.plot(x, y)
plt.show()
fig, ax = plt.subplots(nrows=2,ncols=2)
plt.subplot(2,2,1)
plt.plot(x, y)
plt.subplot(2,2,2)
plt.plot(x, y)
plt.subplot(2,2,3)
plt.plot(x, y)
plt.subplot(2,2,4)
plt.plot(x, y)
plt.show()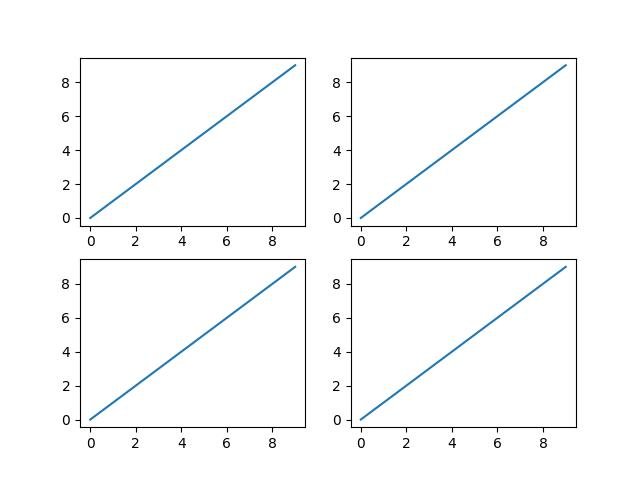
Rotular uma grade de subtrama como uma matriz:
import matplotlib.pyplot as plt
import numpy as np
fig, axes = plt.subplots(
nrows=3, ncols=3,
sharex=True, sharey=True,
figsize=(8,8)
)
x = range(5)
y = range(5)
for row in axes:
for col in row:
col.plot(x, y)
for ax, col in zip(axes[0,:], ['1', '2', '3']):
ax.set_title(col, size=20)
for ax, row in zip(axes[:,0], ['A', 'B', 'C']):
ax.set_ylabel(row, size=20, rotation=0, labelpad=15)
plt.show()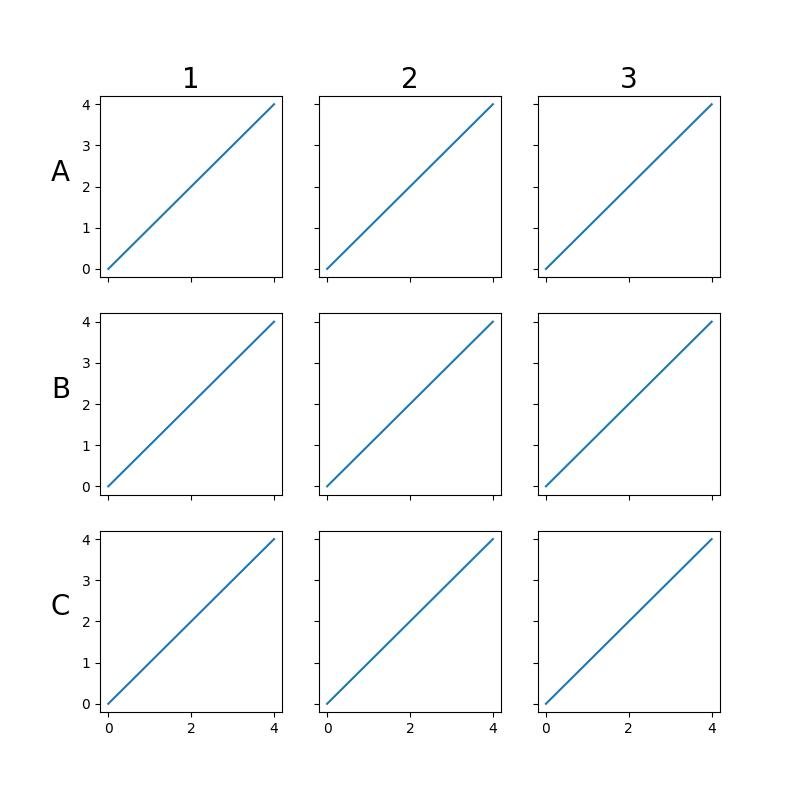
Eixos X e Y compartilhados:
import matplotlib.pyplot as plt
x = range(10)
y = range(10)
fig, ax = plt.subplots(nrows=2,ncols=2, sharex=True, sharey=True)
for row in ax:
for col in row:
col.plot(x, y)
plt.show()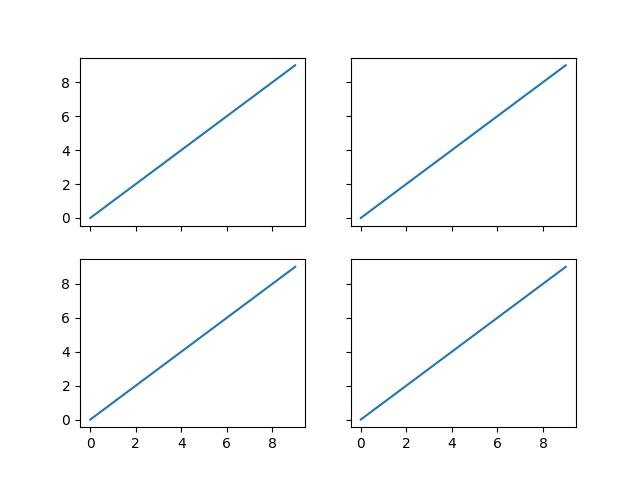
Definindo título e rótulos:
import matplotlib.pyplot as plt
x = range(10)
y = range(10)
fig, ax = plt.subplots(nrows=2,ncols=2)
for row in ax:
for col in row:
col.plot(x, y)
col.set_title('título')
col.set_xlabel('x-axis')
col.set_ylabel('x-axis')
fig.tight_layout()
plt.show()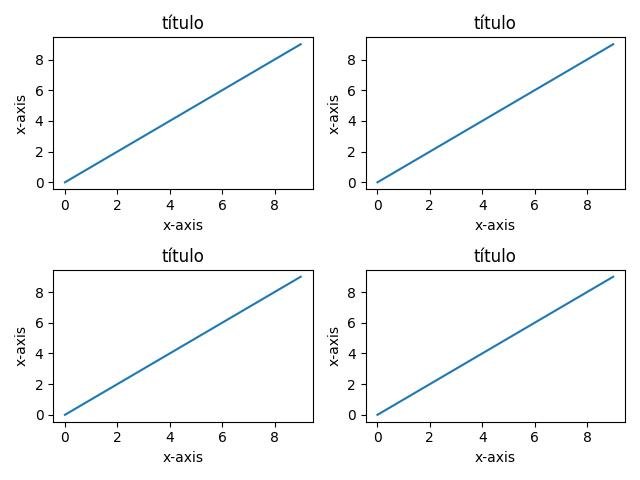
Ocultando subtramas redundantes:
Às vezes, criamos mais subparcelas para um layout retangular (aqui: 3x3) do que realmente precisamos. Aqui está como ocultamos essas subtramas redundantes. Vamos supor que queremos mostrar apenas as 7 primeiras subparcelas.
import matplotlib.pyplot as plt
x = range(10)
y = range(10)
fig, axes = plt.subplots(nrows=3,ncols=3)
for cnt, ax in enumerate(axes.ravel()):
if cnt < 7:
ax.plot(x, y)
else:
ax.axis('off') # hide subplot
plt.show()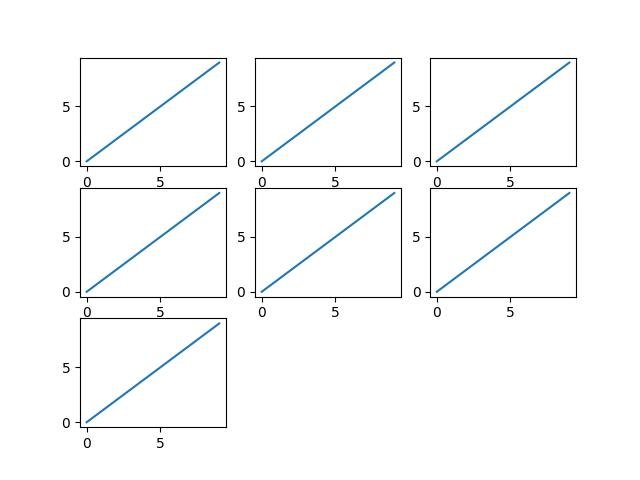
2.1.3.5.2 - Definindo cores
Maneiras d declaração de cores:
Matplotlib suporta 3 maneiras diferentes de codificar cores, por exemplo, se quisermos usar a cor azul, podemos definir as cores como:
- Valores de cores RGB (intervalo de 0,0 a 1,0) -> (0,0, 0,0, 1,0)
- nomes suportados pelo matplotlib -> 'blue' ou 'b'
- Valores hexadecimais HTML -> '#0000FF'
import matplotlib.pyplot as plt
amostras = range(1,4)
for i, col in zip(amostras, [(0.0, 0.0, 1.0), 'blue', '#0000FF']):
plt.plot([0, 10], [0, i], lw=3, color=col)
plt.legend(
['valores RGB: (0.0, 0.0, 1.0)',
"nomes matplotlib: 'blue'",
"valores hex HTML: '#0000FF'"],
loc='upper left')
plt.title('3 alternativas para definir a cor azul')
plt.show()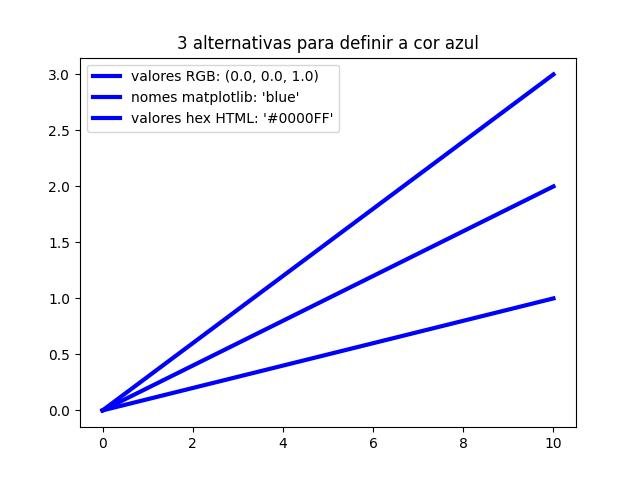
nomes de cores:
Os nomes de cores que são suportados pelo matplotlib são
b: blue (azul)
g: green (verde)
r: red (vermelho)
c: cyan (ciano)
m: magenta (magenta)
y: yellow (yellow)
k: black (black)
w: white (white)
onde a primeira letra representa a versão do atalho.
import matplotlib.pyplot as plt
cols = ['blue', 'green', 'red', 'cyan', 'magenta', 'yellow', 'black', 'white']
amostras = range(1, len(cols)+1)
for i, col in zip(amostras, cols):
plt.plot([0, 10], [0, i], label=col, lw=3, color=col)
plt.legend(loc='upper left')
plt.title('nomes de cores matplotlib')
plt.show()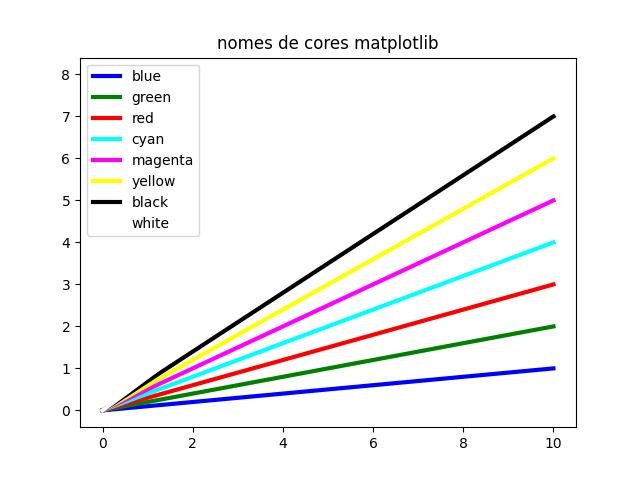
Mapas de cores:
Mais mapas de cores estão disponíveis em Scipy - Mapas de cores.
import numpy as np
import matplotlib.pyplot as plt
fig, (ax0, ax1) = plt.subplots(1,2, figsize=(14, 7))
amostras = range(1,16)
# Ciclo de cores padrão
for i in amostras:
ax0.plot([0, 10], [0, i], label=i, lw=3)
# Mapa de cores
colormap = plt.cm.Paired
plt.gca().set_prop_cycle(color=[colormap(i) for i in np.linspace(0, 0.9, len(amostras))])
for i in amostras:
ax1.plot([0, 10], [0, i], label=i, lw=3)
# Anotações
ax0.set_title('Ciclo de cores padrão')
ax1.set_title('Mapa de cores plt.cm.Paired')
ax0.legend(loc='upper left')
ax1.legend(loc='upper left')
plt.show()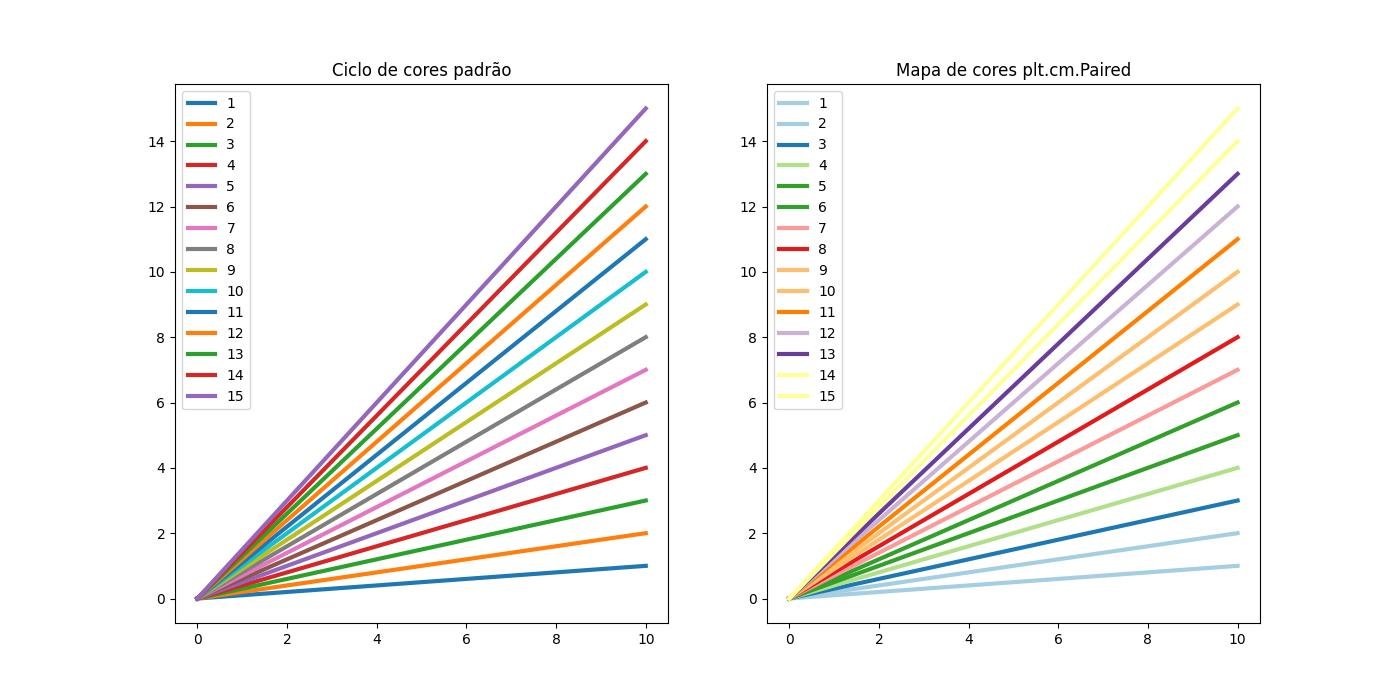
Níveis de cinza:
import matplotlib.pyplot as plt
import numpy as np
plt.figure(figsize=(8,6))
amostras = np.arange(0, 1.1, 0.1)
for i in amostras:
# ! o nível de cinza deve ser analisado como string
plt.plot(
[0, 10], [0, i],
label='gray-level %s'%i, lw=3, color=str(i))
plt.legend(loc='upper left')
plt.title('níveis de cinza')
plt.show()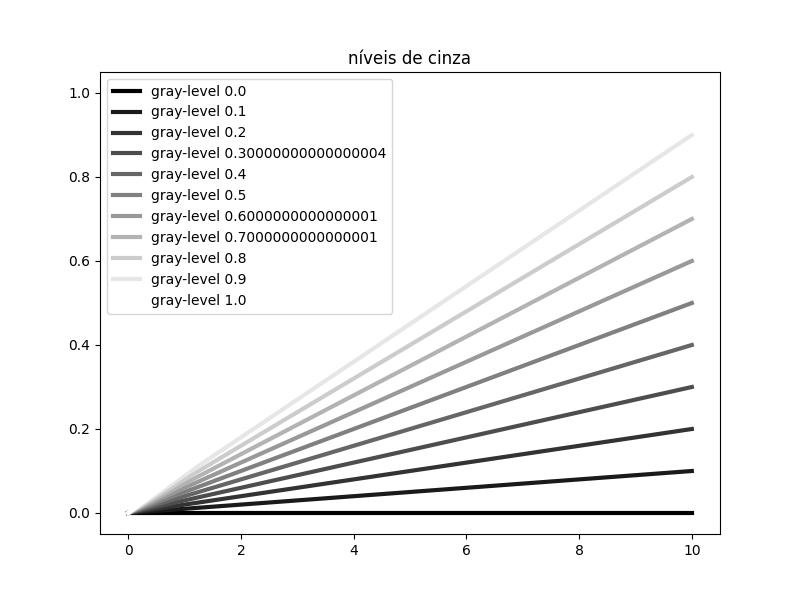
Cores de borda para gráficos de dispersão:
import matplotlib.pyplot as plt
import numpy as np
fig, ax = plt.subplots(nrows=2, ncols=2, figsize=(10,10))
amostras = np.random.randn(30,2)
ax[0][0].scatter(
amostras[:,0], amostras[:,1],
color='red',label='color="red"')
ax[1][0].scatter(
amostras[:,0], amostras[:,1],
c='red',label='c="red"')
ax[0][1].scatter(amostras[:,0], amostras[:,1],
edgecolor='white',
c='red',
label='c="red", edgecolor="white"')
ax[1][1].scatter(amostras[:,0], amostras[:,1],
edgecolor='0',
c='1',
label='color="1.0", edgecolor="0"')
for row in ax:
for col in row:
col.legend(loc='upper left')
plt.show()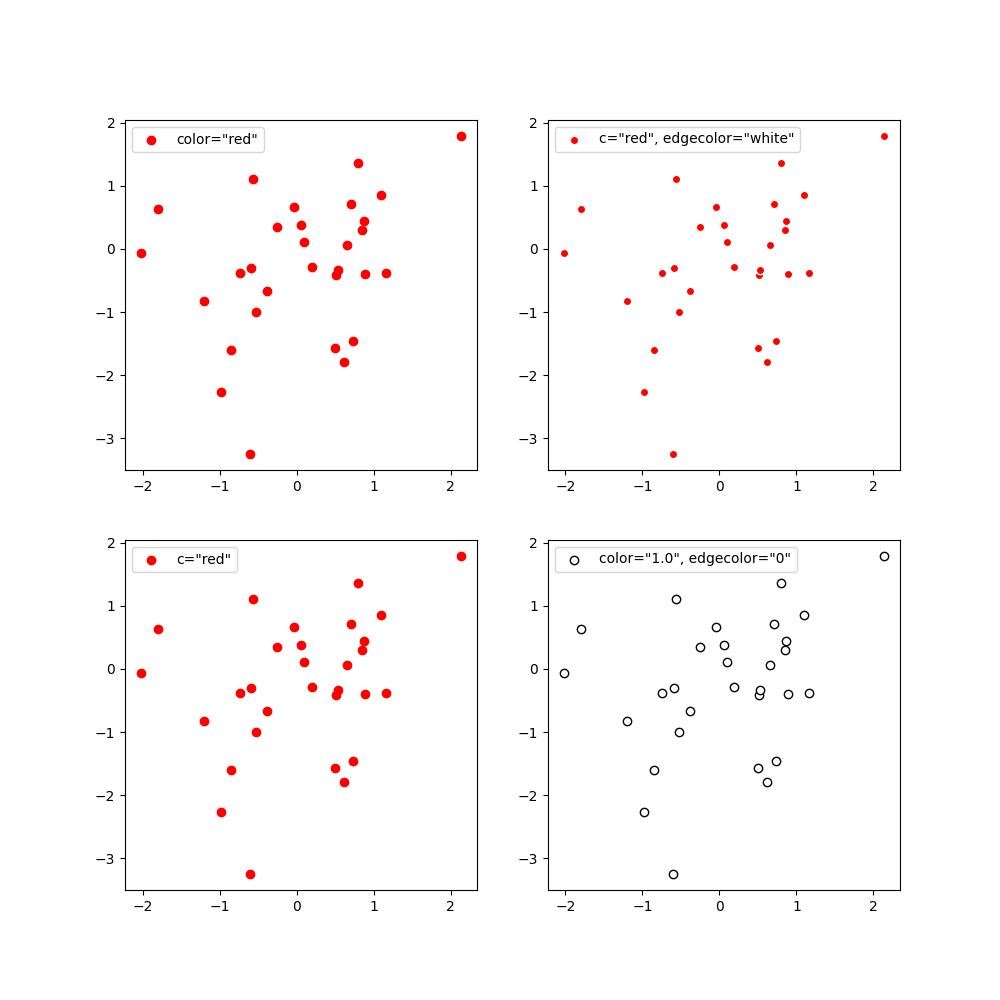
Gradientes de cor:
import matplotlib.pyplot as plt
import matplotlib.colors as col
import matplotlib.cm as cm
import numpy as np
# Dados de entrada
mean_values = np.random.randint(1, 101, 100)
x_pos = range(len(mean_values))
fig = plt.figure(figsize=(20,5))
# Criar mapa de cores
cmap = cm.ScalarMappable(
col.Normalize(min(mean_values),
max(mean_values), cm.hot))
# barras de plotagem
plt.subplot(131)
plt.bar(
x_pos, mean_values, align='center', alpha=0.5,
color=cmap.to_rgba(mean_values))
plt.ylim(0, max(mean_values) * 1.1)
plt.subplot(132)
plt.bar(
x_pos, np.sort(mean_values), align='center', alpha=0.5,
color=cmap.to_rgba(mean_values))
plt.ylim(0, max(mean_values) * 1.1)
plt.subplot(133)
plt.bar(
x_pos, np.sort(mean_values), align='center', alpha=0.5,
color=cmap.to_rgba(np.sort(mean_values)))
plt.ylim(0, max(mean_values) * 1.1)
plt.show()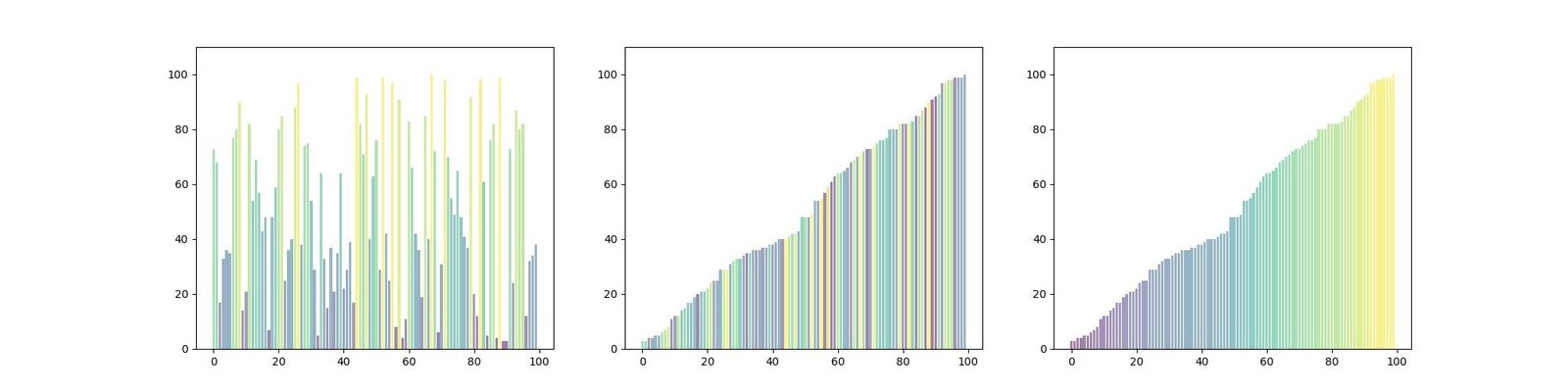
2.1.3.5.3 - Estilos de marcadores
import matplotlib.pyplot as plt
import numpy as np
import matplotlib.pyplot as plt
marcadores = [
'.', # point
',', # pixel
'o', # circle
'v', # triangle down
'^', # triangle up
'<', # triangle_left
'>', # triangle_right
'1', # tri_down
'2', # tri_up
'3', # tri_left
'4', # tri_right
'8', # octagon
's', # square
'p', # pentagon
'*', # star
'h', # hexagon1
'H', # hexagon2
'+', # plus
'x', # x
'D', # diamond
'd', # thin_diamond
'|', # vline
]
plt.figure(figsize=(13, 10))
amostras = range(len(marcadores))
for i in amostras:
plt.plot([i-1, i, i+1], [i, i, i], label=marcadores[i], marker=marcadores[i], markersize=10)
# Anotações
plt.title('Estilos do marcador Matplotlib', fontsize=20)
plt.ylim([-1, len(marcadores)+1])
plt.legend(loc='lower right')
plt.show()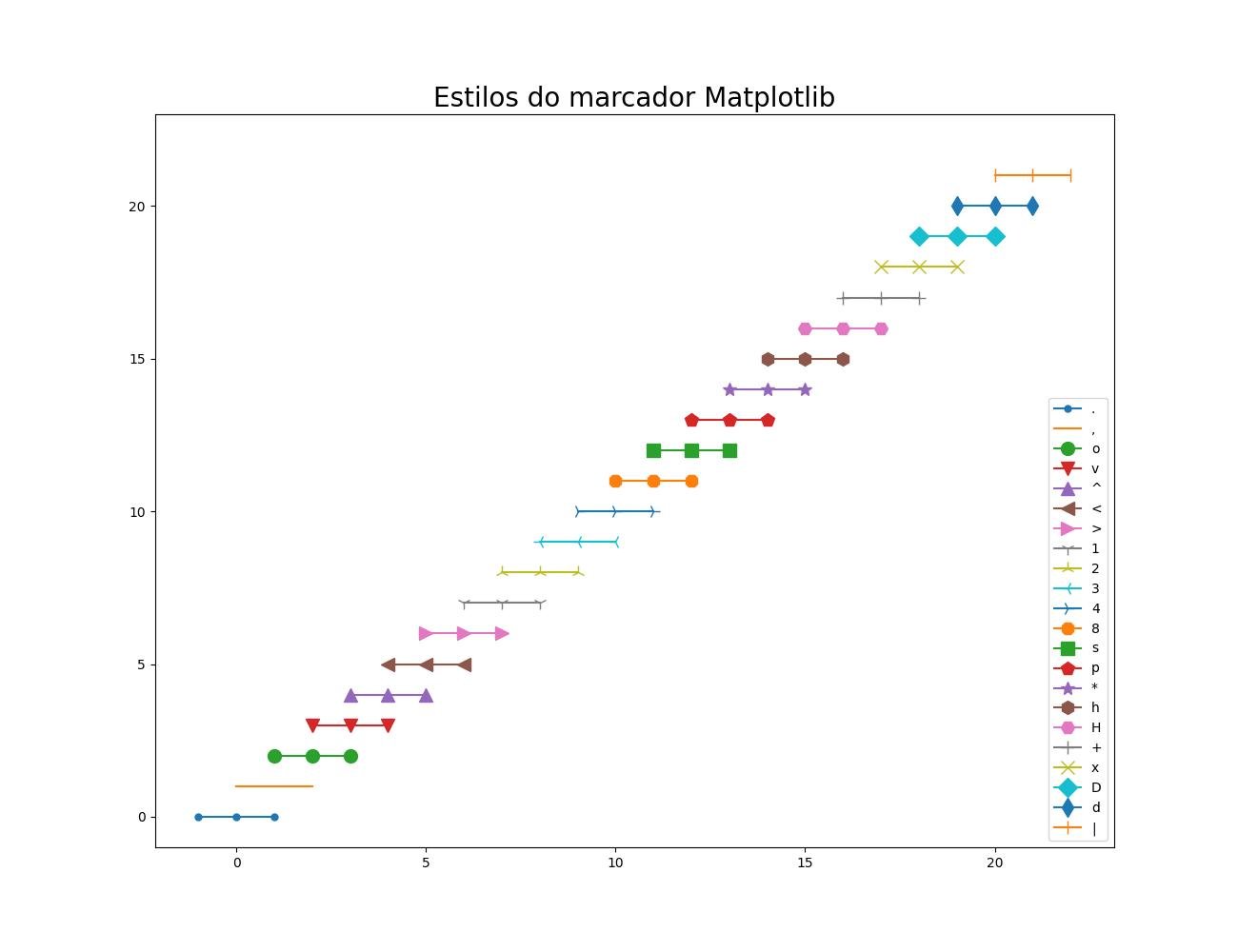
2.1.3.5.4 - Estilos de linha
import numpy as np
import matplotlib.pyplot as plt
estilos_linha = ['-.', '--', 'None', '-', ':']
plt.figure(figsize=(8, 5))
amostras = range(len(estilos_linha))
for i in amostras:
plt.plot(
[i-1, i, i+1], [i, i, i],
label='"%s"' %estilos_linha[i],
linestyle=estilos_linha[i],
lw=4
)
# Anotações
plt.title('Estilos de linha Matplotlib', fontsize=20)
plt.ylim([-1, len(estilos_linha)+1])
plt.legend(loc='lower right')
plt.show()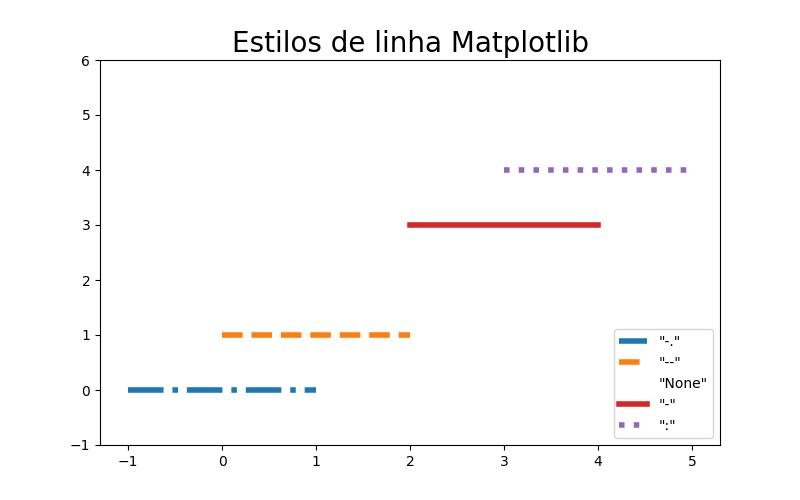
2.1.3.5.5 - Legendas extravagantes e transparentes
import numpy as np
import matplotlib.pyplot as plt
X1 = np.random.randn(100,2)
X2 = np.random.randn(100,2)
X3 = np.random.randn(100,2)
R1 = (X1**2).sum(axis=1)
R2 = (X2**2).sum(axis=1)
R3 = (X3**2).sum(axis=1)
plt.scatter(X1[:,0], X1[:,1],
c='blue',
marker='o',
s=32. * R1,
edgecolor='black',
label='Dataset X1',
alpha=0.7)
plt.scatter(X2[:,0], X2[:,1],
c='gray',
marker='s',
s=32. * R2,
edgecolor='black',
label='Dataset X2',
alpha=0.7)
plt.scatter(X2[:,0], X3[:,1],
c='green',
marker='^',
s=32. * R3,
edgecolor='black',
label='Dataset X3',
alpha=0.7)
plt.xlim([-3,3])
plt.ylim([-3,3])
leg = plt.legend(loc='upper left', fancybox=True)
leg.get_frame().set_alpha(0.5)
plt.show()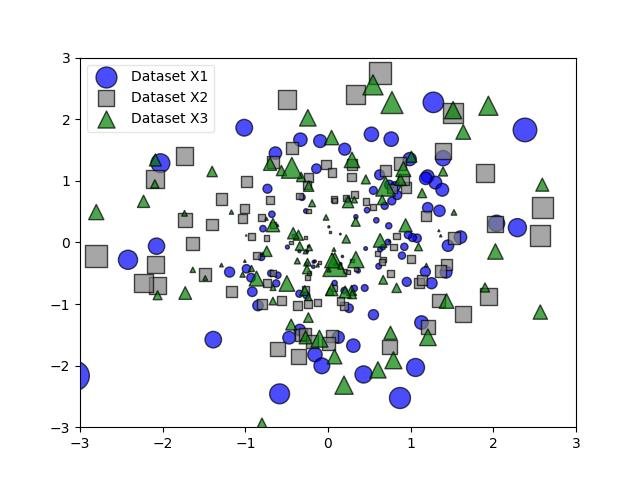
Escondendo eixos e etiquetas:
import numpy as np
import matplotlib.pyplot as plt
x = range(10)
y = range(10)
fig = plt.gca()
plt.plot(x, y)
fig.axes.get_xaxis().set_visible(False)
fig.axes.get_yaxis().set_visible(False)
plt.show()
Removendo quadro e traços:
import numpy as np
import matplotlib.pyplot as plt
x = range(10)
y = range(10)
fig = plt.gca()
plt.plot(x, y)
# removendo quadro
fig.spines["top"].set_visible(False)
fig.spines["bottom"].set_visible(False)
fig.spines["right"].set_visible(False)
fig.spines["left"].set_visible(False)
# removendo carrapatos
plt.tick_params(
axis="both", which="both", bottom="off", top="off",
labelbottom="on", left="off", right="off", labelleft="on")
plt.show()
2.1.3.5.6 - Esquema do eixo estético
import numpy as np
import math
import matplotlib.pyplot as plt
X = np.random.normal(loc=0.0, scale=1.0, size=300)
width = 0.5
bins = np.arange(math.floor(X.min())-width,
math.ceil(X.max())+width,
width) # tamanho fixo da caixa
ax = plt.subplot(111)
# remove axis at the top and to the right
ax.spines["top"].set_visible(False)
ax.spines["right"].set_visible(False)
# ocultar ticks do eixo
plt.tick_params(axis="both", which="both", bottom="off", top="off",
labelbottom="on", left="off", right="off", labelleft="on")
plt.hist(X, alpha=0.5, bins=bins)
plt.grid()
plt.xlabel('x etiqueta')
plt.ylabel('y etiqueta')
plt.title('título')
plt.show()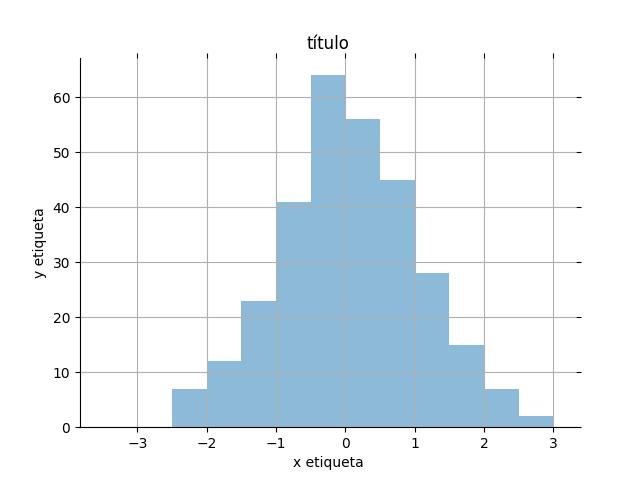
2.1.3.5.7 - Rótulos personalizados
Texto e rotação:
import matplotlib.pyplot as plt
x = range(10)
y = range(10)
labels = ['super long axis label' for i in range(10)]
fig, ax = plt.subplots()
plt.plot(x, y)
# definir rótulos de marca personalizados
ax.set_xticklabels(labels, rotation=45, horizontalalignment='right')
plt.show()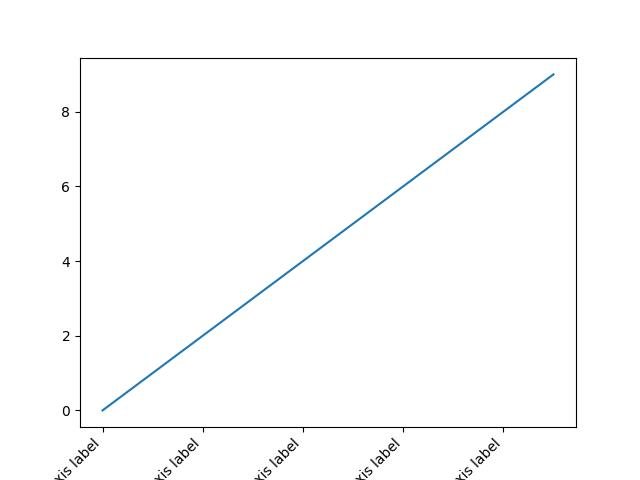
Adicionando um valor constante aos rótulos dos eixos:
import matplotlib.pyplot as plt
CONST = 10
x = range(10)
y = range(10)
labels = [i+CONST for i in x]
fig, ax = plt.subplots()
plt.plot(x, y)
plt.xlabel('x-value + 10')
# definir rótulos de marca personalizados
ax.set_xticklabels(labels)
plt.show()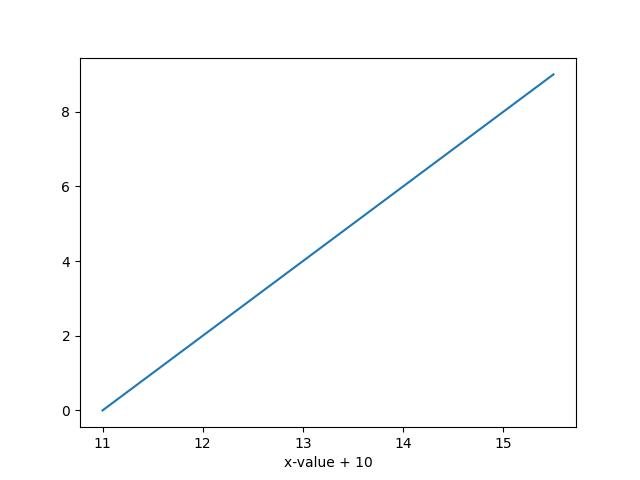
2.1.3.5.8 - Aplicando personalização e configurações globalmente
Todo mundo tem uma percepção diferente de "estilo" e, normalmente, faríamos alguns pequenos ajustes nos visuais padrão do matplotlib aqui e ali. Após a personalização, seria tedioso repetir o mesmo código várias vezes toda vez que produzimos um novo gráfico. No entanto, temos várias opções para aplicar as alterações globalmente.
Configurações apenas para a sessão ativa:
Aqui, estamos interessados apenas nas configurações da sessão atual. Nesse caso, uma maneira de personalizar os padrões do matplotlibs seria o atributo 'rcParams' (na próxima sessão, você verá uma referência útil para todas as diferentes configurações do matplotlib). Por exemplo, se quisermos aumentar o tamanho da fonte de nossos títulos para todos os gráficos que seguem na sessão ativa, podemos digitar o seguinte:
import matplotlib as mpl
mpl.rcParams['axes.titlesize'] = '20'Vejamos como fica:
from matplotlib import pyplot as plt
x = range(10)
y = range(10)
plt.plot(x, y)
plt.title('título maior')
plt.show()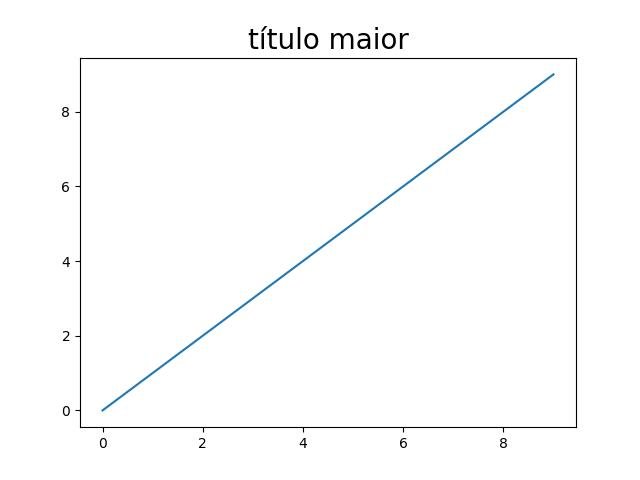
E se quisermos voltar às configurações padrão, podemos usar o comando:
mpl.rcdefaults()Observe que temos que reexecutar a função mágica inline matplotlib depois:
plt.plot(x, y)
plt.title('tamanho do título padrão')
plt.show()
2.1.3.5.9 - Linhas de grade
Gerando alguns dados de amostra:
import numpy as np
import random
from matplotlib import pyplot as plt
data = np.random.normal(0, 20, 1000)
# tamanho fixo da caixa
bins = np.arange(-100, 100, 5) # tamanho fixo da caixa
plt.xlim([min(data)-5, max(data)+5])
plt.hist(data, bins=bins, alpha=0.5)
plt.show()
Grade padrão:
plt.hist(data, bins=bins, alpha=0.5)
plt.grid()
plt.show()
Ou alternativamente:
plt.hist(data, bins=bins, alpha=0.5)
ax = plt.gca()
ax.grid(True)
plt.show()
Grade vertical:
plt.hist(data, bins=bins, alpha=0.5)
ax = plt.gca()
ax.xaxis.grid(True)
plt.show()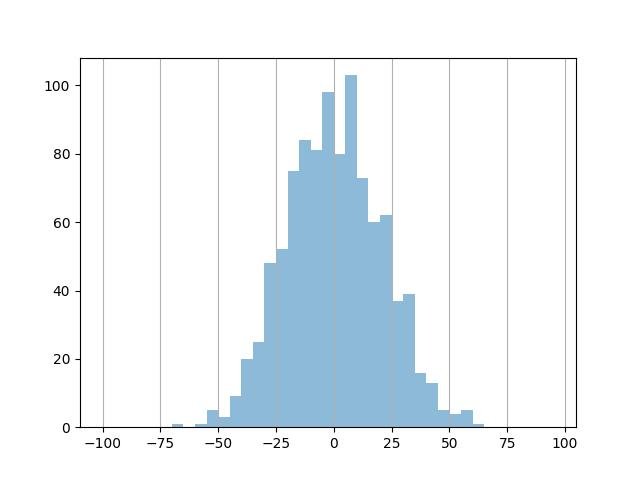
Grade horizontal:
plt.hist(data, bins=bins, alpha=0.5)
ax = plt.gca()
ax.yaxis.grid(True)
plt.show()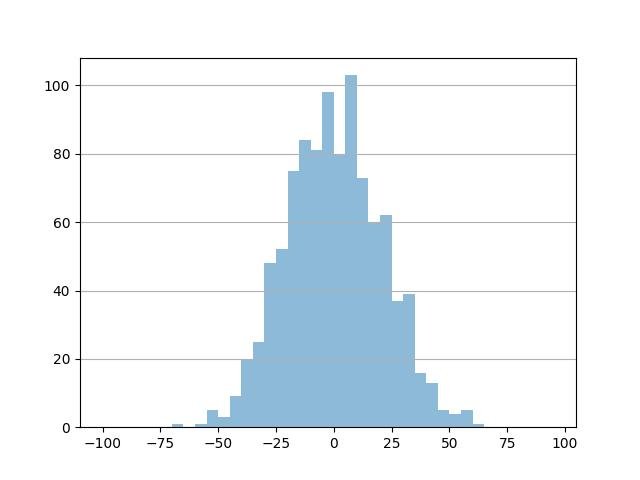
Agora controlamos estilo da linha de grade.
Mudando a frequência do tick:
import numpy as np
# Ticks principais a cada 10
major_ticks = np.arange(-100, 101, 10)
ax = plt.gca()
ax.yaxis.grid()
ax.set_yticks(major_ticks)
plt.hist(data, bins=bins, alpha=0.5)
plt.show()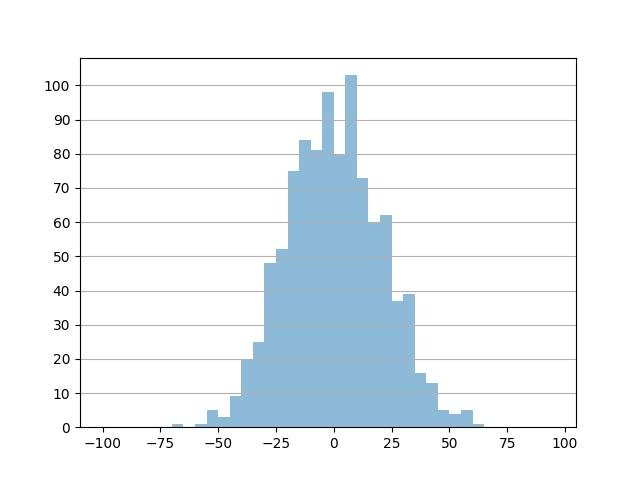
Alterando a cor do tick e o estilo de linha.
from matplotlib import rcParams
rcParams['grid.linestyle'] = '-'
rcParams['grid.color'] = 'blue'
rcParams['grid.linewidth'] = 0.2
plt.grid()
plt.hist(data, bins=bins, alpha=0.5)
plt.show()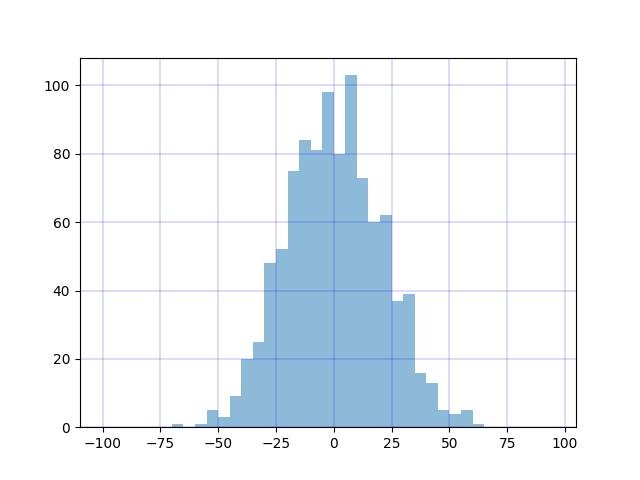
2.1.3.5.10 - Legendas
De volta à estaca zero:
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(10)
for i in range(1, 4):
plt.plot(x, i * x**2, label='Grupo %d' % i)
plt.legend(loc='best')
plt.show()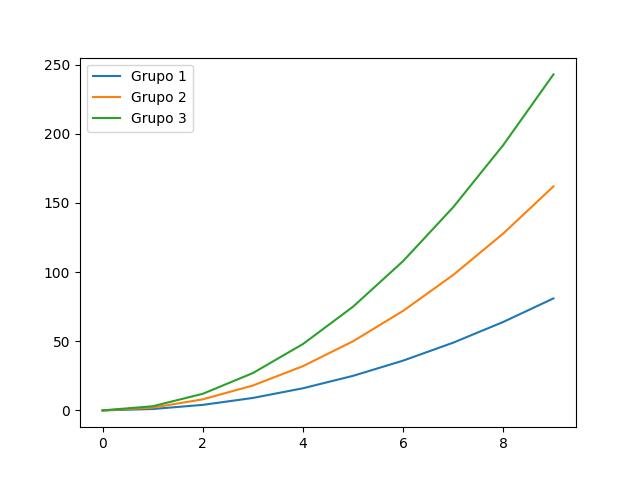
Vamos ficar chiques:
x = np.arange(10)
for i in range(1, 4):
plt.plot(x, i * x**2, label='Grupo %d' % i)
plt.legend(loc='best', fancybox=True, shadow=True)
plt.show()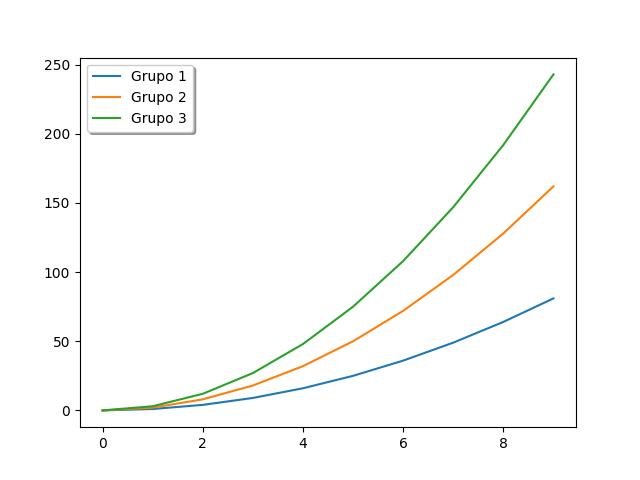
Pensando fora da caixa:
fig = plt.figure()
ax = plt.subplot(111)
x = np.arange(10)
for i in range(1, 4):
ax.plot(x, i * x**2, label='Grupo %d' % i)
ax.legend(loc='upper center',
bbox_to_anchor=(0.5, # horizontal
1.15),# vertical
ncol=3, fancybox=True)
plt.show()
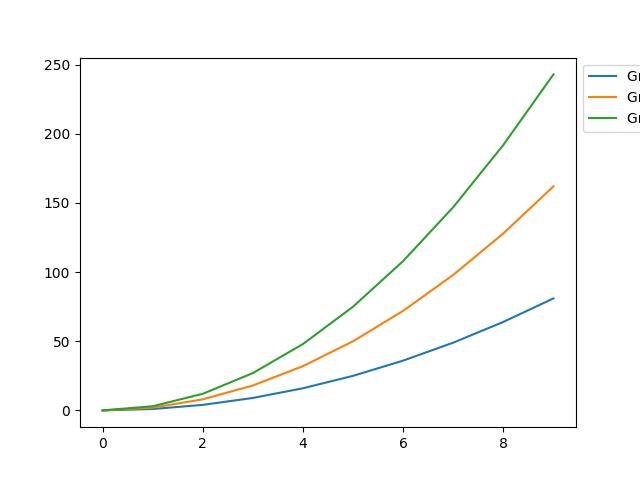
fig = plt.figure()
ax = plt.subplot(111)
x = np.arange(10)
for i in range(1, 4):
ax.plot(x, i * x**2, label='Grupo %d' % i)
ax.legend(
loc='upper left',
bbox_to_anchor=(1., 1.),
ncol=1, fancybox=True)
plt.show()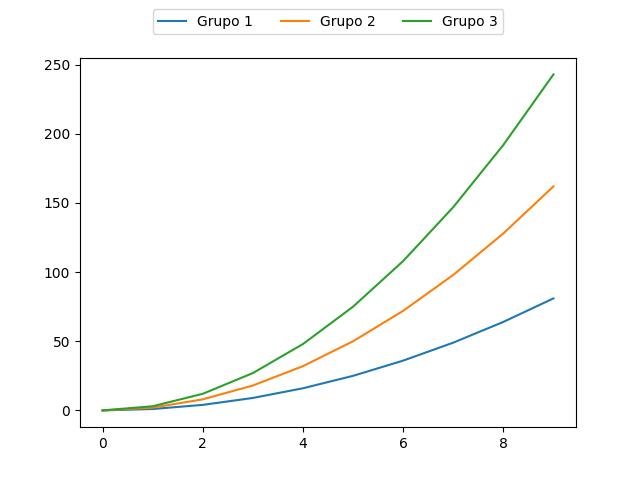
Amo quando as coisas são transparentes, livres e claras:
x = np.arange(10)
for i in range(1, 4):
plt.plot(x, i * x**2, label='Grupo %d' % i)
plt.legend(loc='upper right', framealpha=0.1)
plt.show()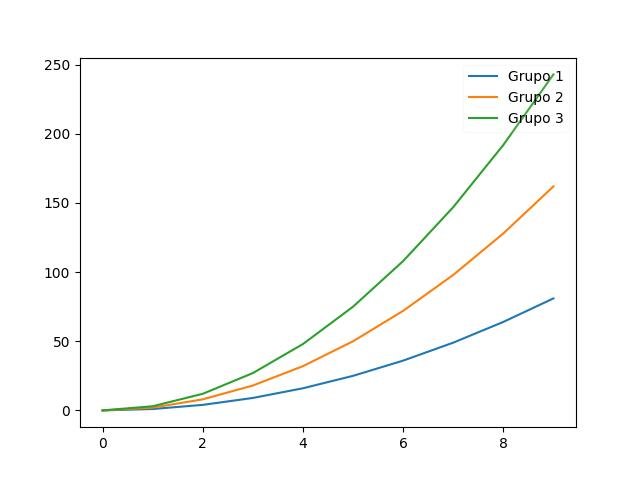
Marcadores: Todas as coisas boas vêm em trios!
from itertools import cycle
x = np.arange(10)
colors = ['blue', 'red', 'green']
color_gen = cycle(colors)
for i in range(1, 4):
plt.scatter(x, i * x**2, label='Grupo %d' % i, color=next(color_gen))
plt.legend(loc='upper left')
plt.show()
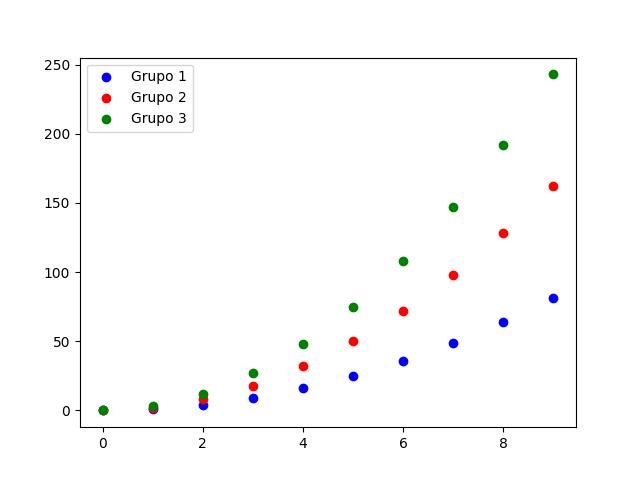
from itertools import cycle
x = np.arange(10)
colors = ['blue', 'red', 'green']
color_gen = cycle(colors)
for i in range(1, 4):
plt.scatter(x, i * x**2, label='Grupo %d' % i, color=next(color_gen))
plt.legend(loc='upper left', scatterpoints=1)
plt.show()
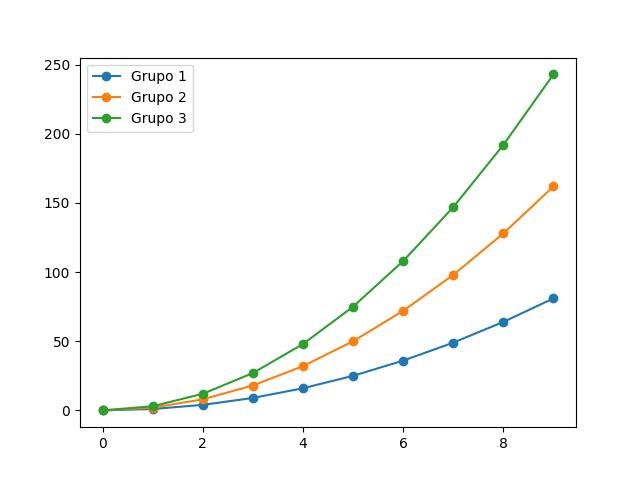
from itertools import cycle
x = np.arange(10)
colors = ['blue', 'red', 'green']
color_gen = cycle(colors)
for i in range(1, 4):
plt.plot(x, i * x**2, label='Grupo %d' % i, marker='o')
plt.legend(loc='upper left')
plt.show()
from itertools import cycle
x = np.arange(10)
colors = ['blue', 'red', 'green']
color_gen = cycle(colors)
for i in range(1, 4):
plt.plot(x, i * x**2, label='Grupo %d' % i, marker='o')
plt.legend(loc='upper left', numpoints=1)
plt.show()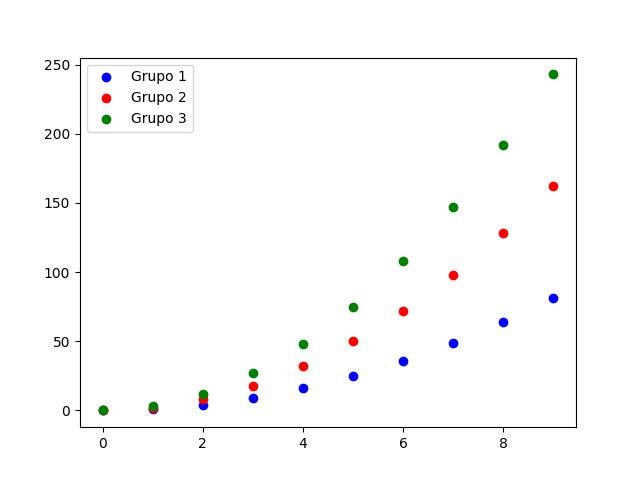
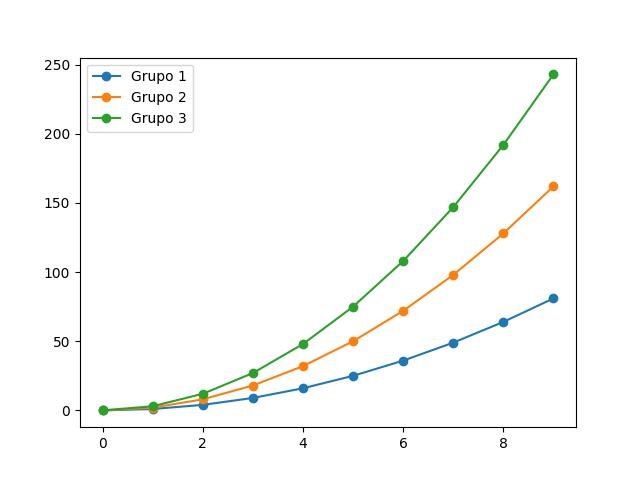
2.1.3.5.11 - Folhas de estilo
Um dos recursos mais legais adicionados ao matlotlib é o suporte para "estilos"!
A funcionalidade de "estilos" nos permite criar belos gráficos sem problemas, sendo um ótimo recurso!
Os estilos atualmente incluídos podem ser listados via print(plt.style.available):
import matplotlib.pyplot as plt
print(plt.style.available)Existem duas maneiras de aplicar o estilo aos nossos gráficos.
Primeiro, podemos definir o estilo para nosso ambiente de codificação globalmente por meio da função plt.style.use():
import numpy as np
plt.style.use('ggplot')
x = np.arange(10)
for i in range(1, 4):
plt.plot(x, i * x**2, label='Group %d' % i)
plt.legend(loc='best')
plt.show()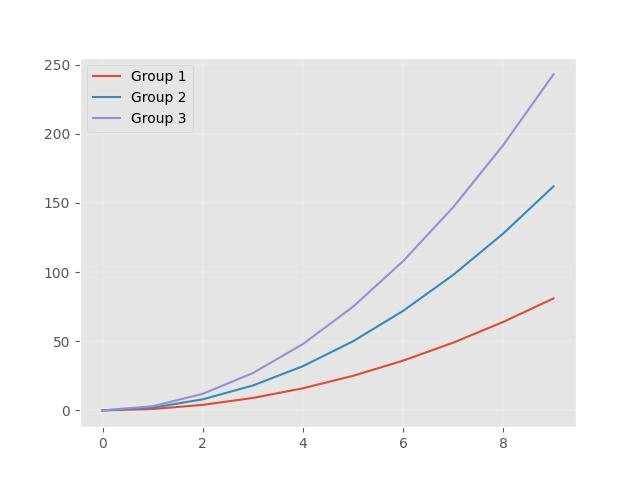
Outra maneira de usar estilos é por meio do gerenciador de contexto, que aplica o estilo apenas a um bloco de código específico:
with plt.style.context('fivethirtyeight'):
for i in range(1, 4):
plt.plot(x, i * x**2, label='Group %d' % i)
plt.legend(loc='best')
plt.show()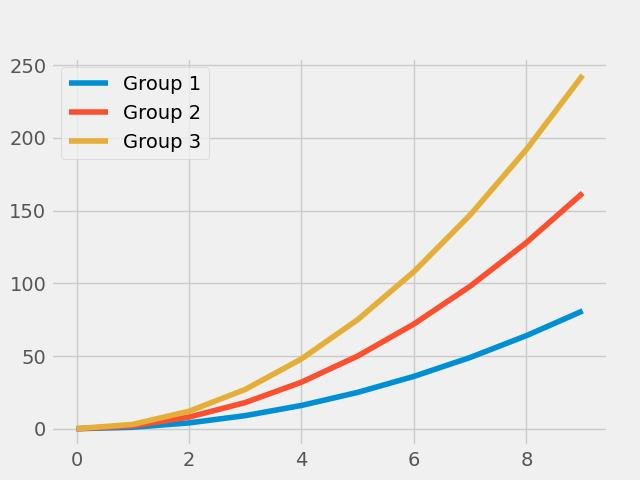
Finalmente, aqui está uma visão geral de como os diferentes estilos se parecem:
import math
n = len(plt.style.available)
num_rows = math.ceil(n/4)
fig = plt.figure(figsize=(15, 15))
for i, s in enumerate(plt.style.available):
with plt.style.context(s):
ax = fig.add_subplot(num_rows, 4, i+1)
for i in range(1, 4):
ax.plot(x, i * x**2, label='Group %d' % i)
ax.set_xlabel(s, color='black')
ax.legend(loc='best')
fig.tight_layout()
plt.show()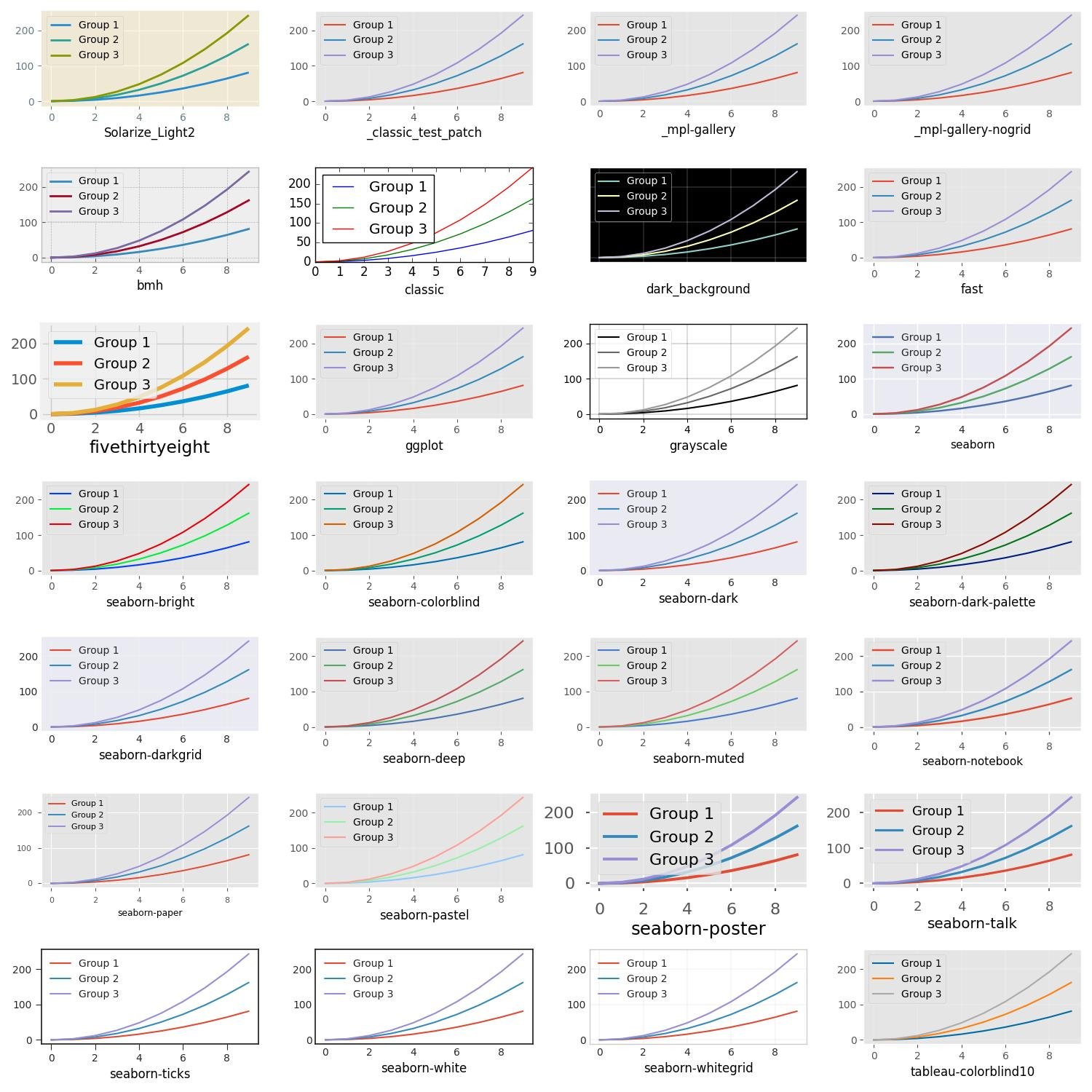
2.1.3.6 - Mapas de calor
Iniciamos importando os pacotes necessários:
import numpy as np
import matplotlib.pyplot as pltCriamos as matrizes:
# Amostra de uma distribuição gaussiana bivariada
mean = [0,0]
cov = [[0,1],[1,0]]
x, y = np.random.multivariate_normal(mean, cov, 10000).T2.1.3.6.1 - Mapas de calor simples
Usando o histogram2d do NumPy:
hist, xedges, yedges = np.histogram2d(x,y)
X,Y = np.meshgrid(xedges,yedges)
plt.imshow(hist)
plt.grid(True)
plt.colorbar()
plt.show()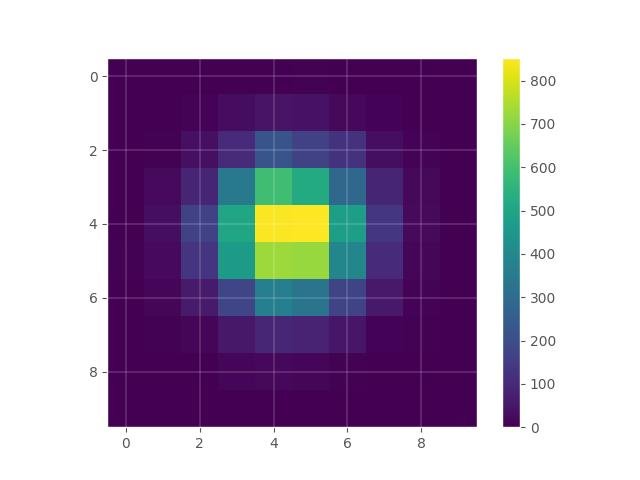
Mudando a interpolação:
plt.imshow(hist, interpolation='nearest')
plt.grid(True)
plt.colorbar()
plt.show()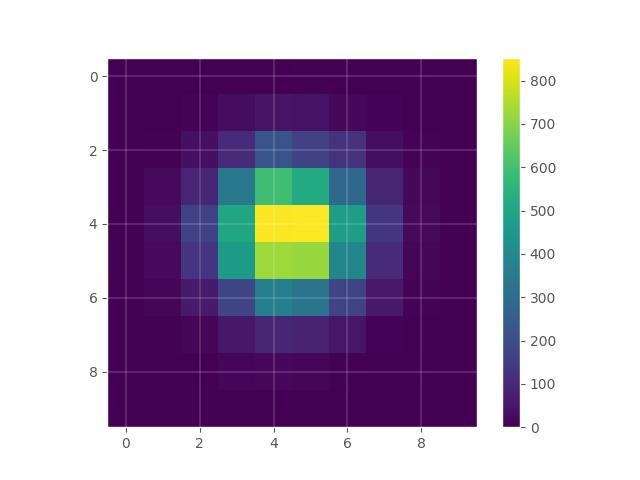
Usando hist2d de matplotlib:
plt.hist2d(x, y, bins=10)
plt.colorbar()
plt.grid()
plt.show()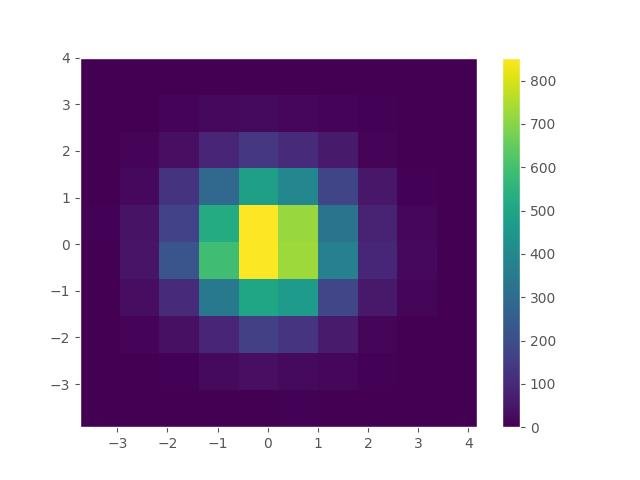
alterando o tamanho da caixa:
plt.hist2d(x, y, bins=40)
plt.colorbar()
plt.grid()
plt.show()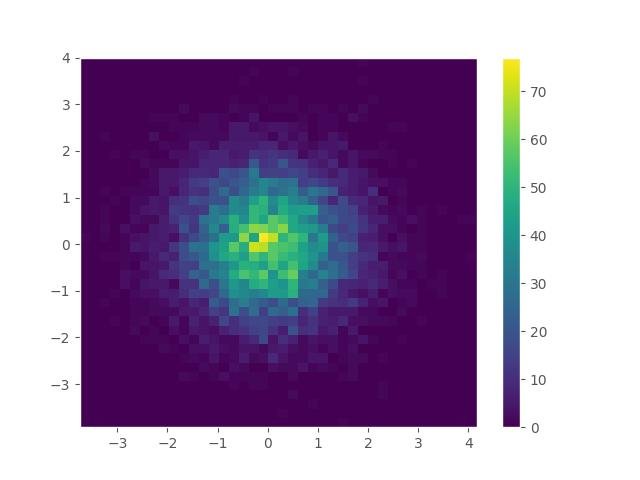
Usando pcolor do matplotlib:
plt.pcolor(hist)
plt.colorbar()
plt.grid()
plt.show()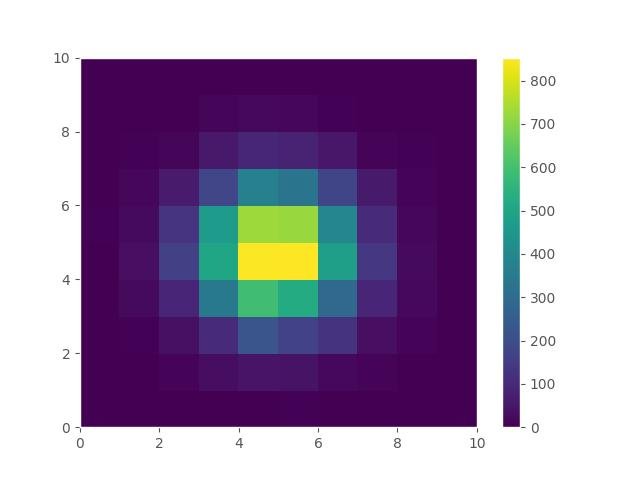
Usando a função matshow() de matplotlib:
import numpy as np
import matplotlib.pyplot as plt
columns = ['A', 'B', 'C', 'D']
rows = ['1', '2', '3', '4']
data = np.random.random((4,4))
fig = plt.figure()
ax = fig.add_subplot(111)
cax = ax.matshow(data, interpolation='nearest')
fig.colorbar(cax)
ax.set_xticklabels([''] + columns)
ax.set_yticklabels([''] + rows)
plt.show()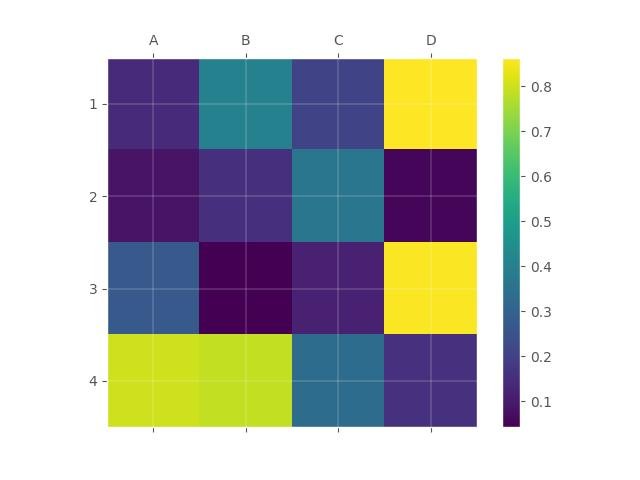
2.1.3.6.2 - Usando diferentes mapas de cores
Mapas de cores disponíveis:
from math import ceil
import numpy as np
# Sample from a bivariate Gaussian distribution
mean = [0,0]
cov = [[0,1],[1,0]]
x, y = np.random.multivariate_normal(mean, cov, 10000).T
size = len(plt.cm.datad.keys())
all_maps = list(plt.cm.datad.keys())
fig, ax = plt.subplots(ceil(size/4), 4, figsize=(12,100))
counter = 0
for row in ax:
for col in row:
try:
col.imshow(hist, cmap=all_maps[counter])
col.set_title(all_maps[counter])
except IndexError:
break
counter += 1
plt.tight_layout()
plt.show()
2.1.3.6.3 - Novos mapas de cores
Novos mapas de cores projetados por Stéfan van der Walt e Nathaniel Smith foram incluídos no matplotlib 1.5, e o mapa de cores viridis será o novo mapa de cores padrão no matplotlib 2.0.
from math import ceil
import numpy as np
from matplotlib import pyplot as plt
# Sample from a bivariate Gaussian distribution
mean = [0,0]
cov = [[0,1],[1,0]]
x, y = np.random.multivariate_normal(mean, cov, 10000).T
size = len(plt.cm.datad.keys())
all_maps = list(plt.cm.datad.keys())
new_maps = ['viridis', 'inferno', 'magma', 'plasma']
counter = 0
for i in range(4):
plt.subplot(1, 4, counter + 1)
plt.imshow(hist, cmap=new_maps[counter])
plt.title(new_maps[counter])
counter += 1
plt.tight_layout()
plt.show()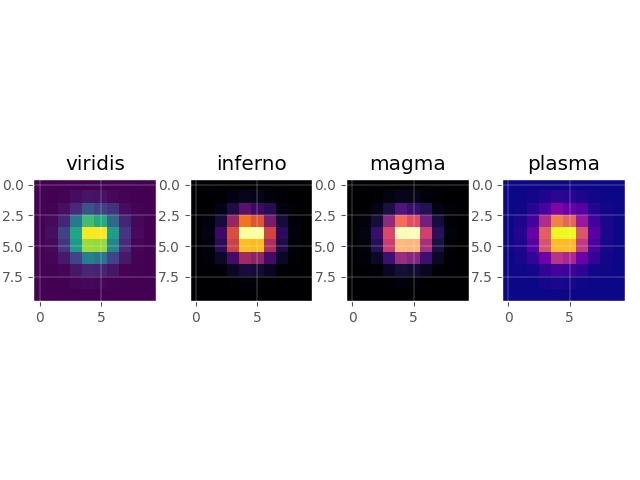
Criando mapas de calor com um mapa de cores em escala logarítmica:
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm
import numpy as np
np.random.seed(1)
a = np.random.random((25, 25))
plt.subplot(1, 1, 1)
plt.pcolor(a, norm=LogNorm(vmin=a.min() / 1.2, vmax=a.max() * 1.2), cmap='PuBu_r')
plt.colorbar()
plt.show()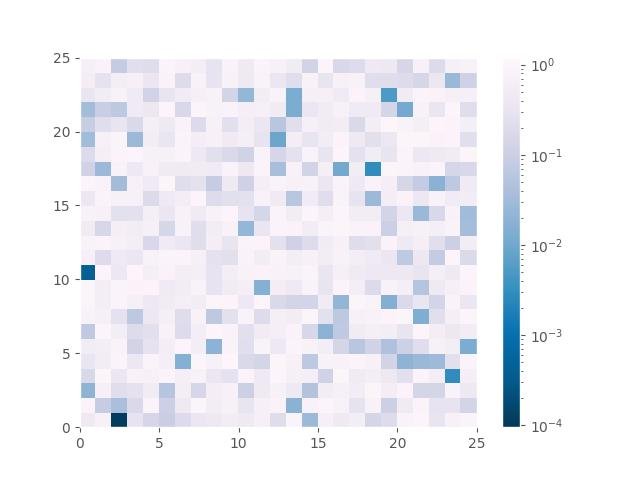
2.1.3.7 - Histogramas
2.1.3.7.1 - Histogramas simples
Tamanho do compartimento fixo:
import numpy as np
import random
from matplotlib import pyplot as plt
data = np.random.normal(0, 20, 1000)
# tamanho fixo da caixa
bins = np.arange(-100, 100, 5) # tamanho fixo da caixa
plt.xlim([min(data)-5, max(data)+5])
plt.hist(data, bins=bins, alpha=0.5)
plt.title('Dados gaussianos aleatórios (tamanho fixo da caixa)')
plt.xlabel('variável X (bin size = 5)')
plt.ylabel('contagem')
plt.show()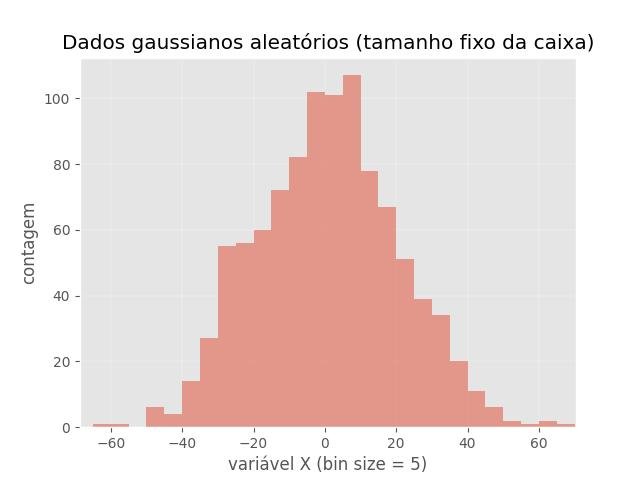
Número fixo de caixas:
import numpy as np
import random
import math
from matplotlib import pyplot as plt
data = np.random.normal(0, 20, 1000)
bins = np.linspace(math.ceil(min(data)),
math.floor(max(data)),
20) # fixed number of bins
plt.xlim([min(data)-5, max(data)+5])
plt.hist(data, bins=bins, alpha=0.5)
plt.title('Dados gaussianos aleatórios (número fixo de compartimentos)')
plt.xlabel('variável X (20 evenly spaced bins)')
plt.ylabel('contagem')
plt.show()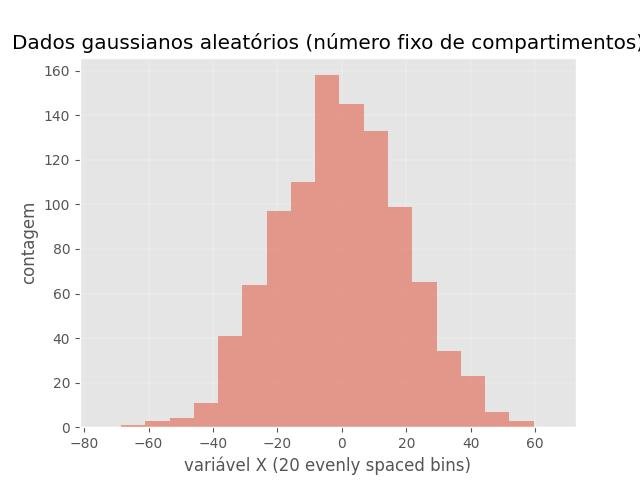
2.1.3.7.2 - Histograma de 2 conjuntos de dados sobrepostos
import numpy as np
import random
from matplotlib import pyplot as plt
data1 = [random.gauss(15,10) for i in range(500)]
data2 = [random.gauss(5,5) for i in range(500)]
bins = np.arange(-60, 60, 2.5)
plt.xlim([min(data1+data2)-5, max(data1+data2)+5])
plt.hist(data1, bins=bins, alpha=0.3, label='class 1')
plt.hist(data2, bins=bins, alpha=0.3, label='class 2')
plt.title('Dados gaussianos aleatórios')
plt.xlabel('variável X')
plt.ylabel('contagem')
plt.legend(loc='upper right')
plt.show()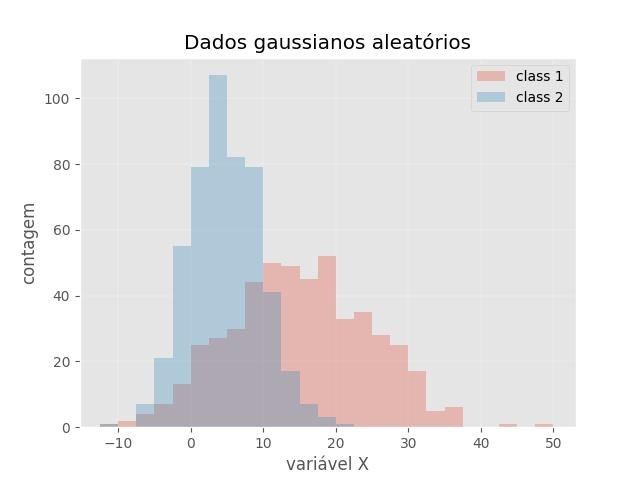
import numpy as np
import random
import math
from matplotlib import pyplot as plt
from scipy.interpolate import interp1d
from scipy.stats import norm
data = np.random.normal(0, 20, 10000)
# traçando o histograma
n, bins, patches = plt.hist(data, bins=20, alpha=0.5, color='lightblue')
# ajustando os dados
mu, sigma = norm.fit(data)
# adicionando a linha ajustada
y = norm.pdf(bins, mu, sigma)
interp = interp1d(bins, y, kind='cubic')
plt.plot(bins, interp(y), linewidth=2, color='blue')
plt.xlim([min(data)-5, max(data)+5])
plt.title('Dados gaussianos aleatórios (número fixo de compartimentos)')
plt.xlabel('variável X (20 evenly spaced bins)')
plt.ylabel('contagem')
plt.show()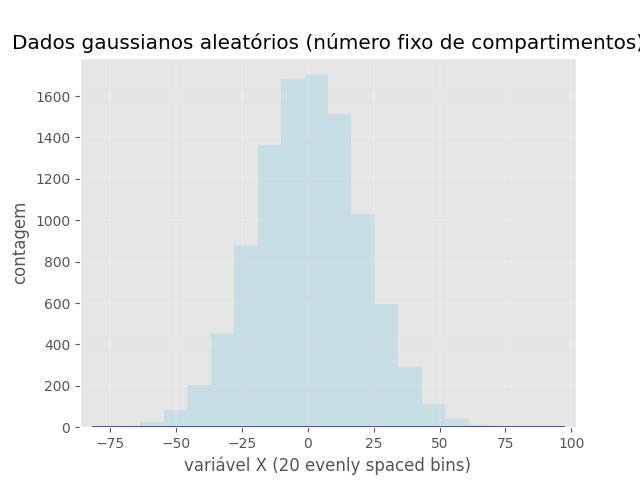
2.1.3.7.3 - Histograma mostrando as alturas das barras, mas sem a área sob as barras
O gráfico de linha abaixo está usando compartimentos de um histograma e é particularmente útil se você estiver trabalhando com muitos conjuntos de dados sobrepostos diferentes.
# Gera um conjunto de dados gaussiano aleatório com diferentes meios
# 5 linhas com 30 colunas, onde cada linha representa 1 amostra.
import numpy as np
data = np.ones((5,30))
for i in range(5):
data[i,:] = np.random.normal(loc=i/2, scale=1.0, size=30)Por meio da função np.histogram(), podemos categorizar nossos dados em compartimentos distintos.
from math import floor, ceil # para arredondar para cima e para baixo
data_min = floor(data.min()) # minimum val. of the dataset rounded down
data_max = floor(data.max()) # maximum val. of the dataset rounded up
bin_size = 0.5
bins = np.arange(floor(data_min), ceil(data_max), bin_size)
print(np.histogram(data[0,:], bins=bins))A função numpy.histogram retorna uma tupla, onde o primeiro valor é uma matriz de quantas amostras caem no primeiro compartimento, no segundo compartimento e assim por diante.
O segundo valor é outro array NumPy; ele contém os compartimentos especificados. Observe que todos os bins, exceto o último, são intervalos semi-abertos, por exemplo, o primeiro bin seria [-2, -1,5) (incluindo -2, mas não incluindo -1,5) e o segundo bin seria [-1,5, - 1.) (incluindo -1,5, mas não incluindo 1,0). Mas o último bin é definido como [2., 2.5] (incluindo 2 e incluindo 2.5).
from matplotlib import pyplot as plt
marcadores = ['^', 'v', 'o', 'p', 'x', 's', 'p', ',']
plt.figure(figsize=(13,8))
for row in range(data.shape[0]):
hist = np.histogram(data[row,:], bins=bins)
plt.errorbar(hist[1][:-1] + bin_size/2,
hist[0],
alpha=0.3,
xerr=bin_size/2,
capsize=0,
fmt=marcadores[row],
linewidth=8,
)
plt.legend(['sample %s'%i for i in range(1, 6)])
plt.grid()
plt.title('Histograma mostrando as alturas das barras, mas sem a área sob as barras', fontsize=18)
plt.ylabel('contagem', fontsize=14)
plt.xlabel('Valor de X value (tamanho do compartimento = %s)'%bin_size, fontsize=14)
plt.xticks(bins + bin_size)
plt.show()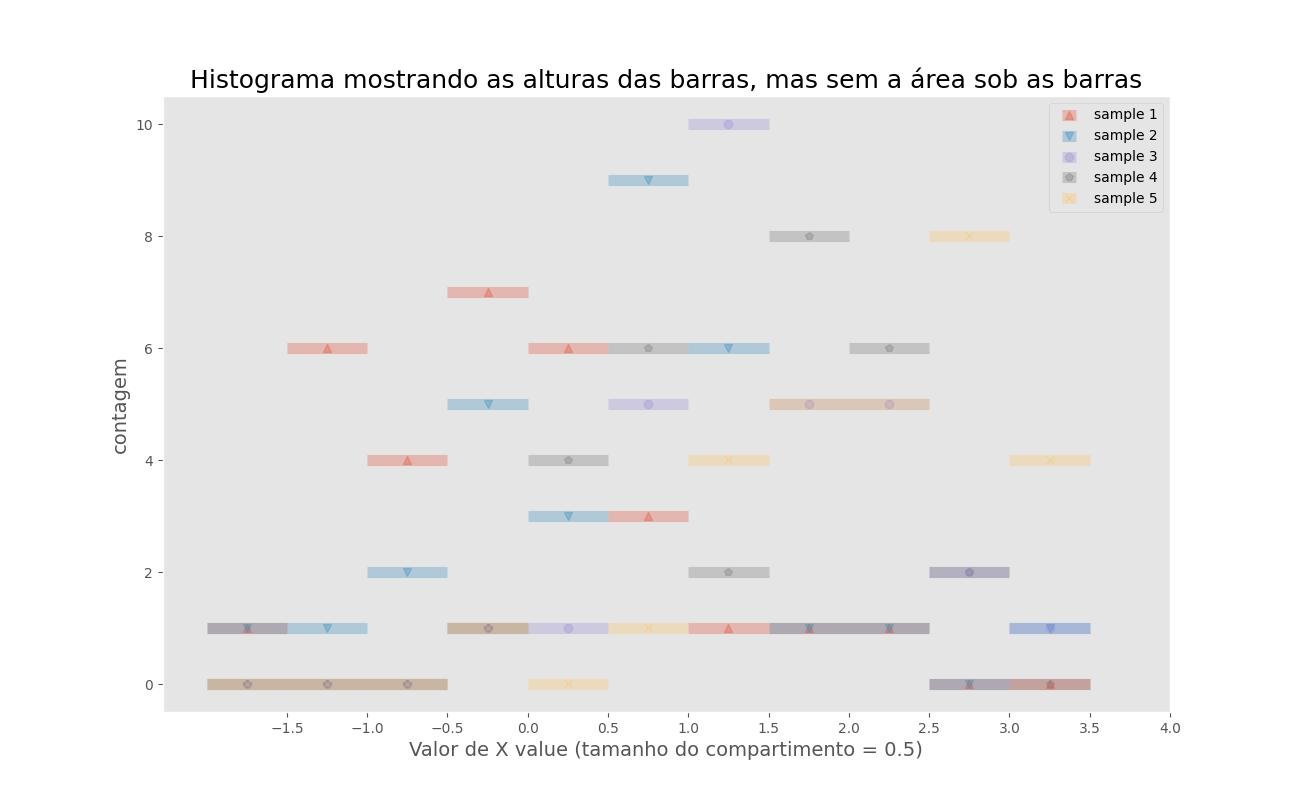
2.1.3.8 - Gráficos de linhas
2.1.3.8.1 - Simple line plot
import matplotlib.pyplot as plt
x = [1, 2, 3]
y_1 = [50, 60, 70]
y_2 = [20, 30, 40]
plt.plot(x, y_1, marker='x')
plt.plot(x, y_2, marker='^')
plt.xlim([0, len(x)+1])
plt.ylim([0, max(y_1+y_2) + 10])
plt.xlabel('x-axis etiqueta')
plt.ylabel('y-axis etiqueta')
plt.title('Gráfico de linha simples')
plt.legend(['amostra 1', 'amostra 2'], loc='upper left')
plt.show()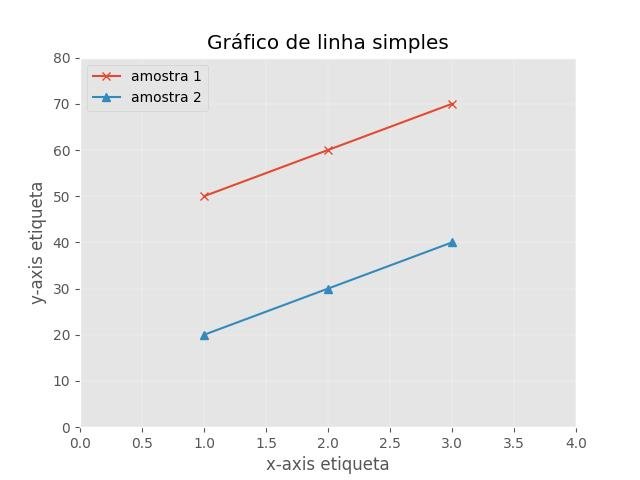
2.1.3.8.2 - Gráfico de linha com barras de erro
import matplotlib.pyplot as plt
x = [1, 2, 3]
y_1 = [50, 60, 70]
y_2 = [20, 30, 40]
y_1_err = [4.3, 4.5, 2.0]
y_2_err = [2.3, 6.9, 2.1]
x_labels = ["x1", "x2", "x3"]
plt.errorbar(x, y_1, yerr=y_1_err, fmt='-x')
plt.errorbar(x, y_2, yerr=y_2_err, fmt='-^')
plt.xticks(x, x_labels)
plt.xlim([0, len(x)+1])
plt.ylim([0, max(y_1+y_2) + 10])
plt.xlabel('x-axis etiqueta')
plt.ylabel('y-axis etiqueta')
plt.title('Gráfico de linha com barras de erro')
plt.legend(['amostra 1', 'amostra 2'], loc='upper left')
plt.show()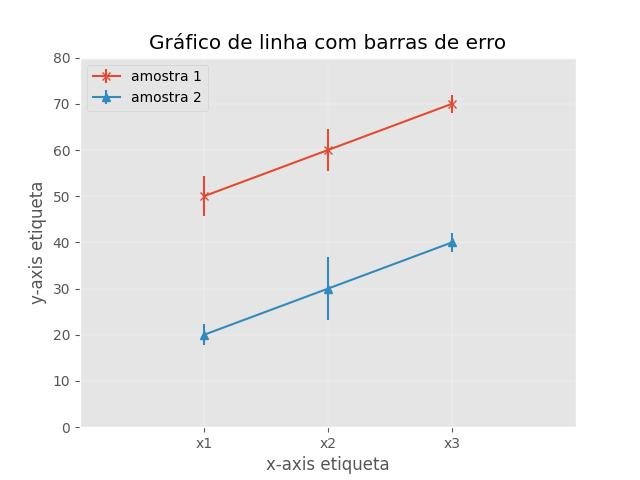
2.1.3.8.3 - plot with x-axis labels and log-scale
import matplotlib.pyplot as plt
x = [1, 2, 3]
y_1 = [0.5,7.0,60.0]
y_2 = [0.3,6.0,30.0]
x_labels = ["x1", "x2", "x3"]
plt.plot(x, y_1, marker='x')
plt.plot(x, y_2, marker='^')
plt.xticks(x, x_labels)
plt.xlim([0,4])
plt.xlabel('x-axis etiqueta')
plt.ylabel('y-axis etiqueta')
plt.yscale('log')
plt.title('Gráfico de linhas com rótulos do eixo x e escala logarítmica')
plt.legend(['amostra 1', 'amostra 2'], loc='upper left')
plt.show()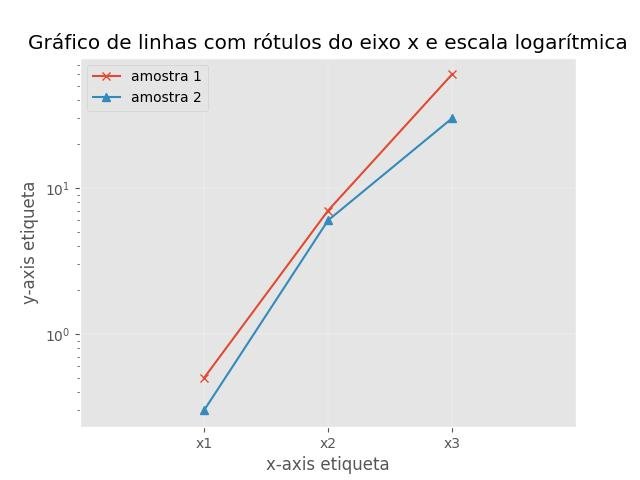
2.1.3.8.4 - Gaussian probability density functions
import numpy as np
from matplotlib import pyplot as plt
import math
def pdf(x, mu=0, sigma=1):
"""
Calculates the normal distribution's probability density
function (PDF).
"""
term1 = 1.0 / ( math.sqrt(2*np.pi) * sigma )
term2 = np.exp( -0.5 * ( (x-mu)/sigma )**2 )
return term1 * term2
x = np.arange(0, 100, 0.05)
pdf1 = pdf(x, mu=5, sigma=2.5**0.5)
pdf2 = pdf(x, mu=10, sigma=6**0.5)
plt.plot(x, pdf1)
plt.plot(x, pdf2)
plt.title('Funções de densidade de probabilidade')
plt.ylabel('p(x)')
plt.xlabel('variável aleatória x')
plt.legend(['pdf1 ~ N(5,2.5)', 'pdf2 ~ N(10,6)'], loc='upper right')
plt.ylim([0,0.5])
plt.xlim([0,20])
plt.show()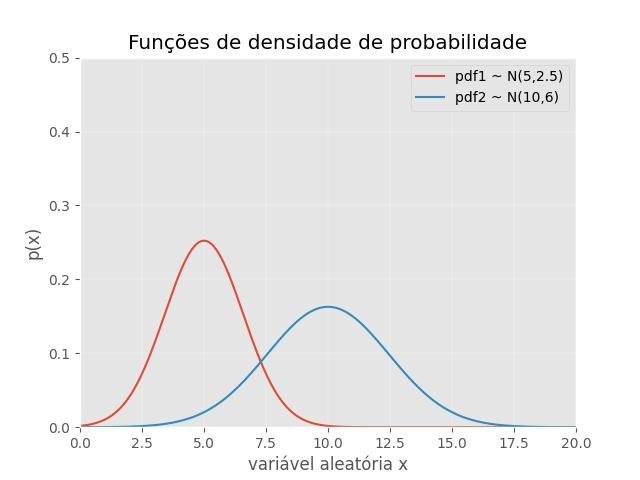
2.1.3.8.5 - Parcelas cumulativas
Soma cumulativa:
import numpy as np
import matplotlib.pyplot as plt
# soma cumulativa com np.cumsum()
A = np.arange(1, 11)
B = np.random.randn(10) # 10 rand. values from a std. norm. distr.
C = B.cumsum()
# São subplotados dois gráficosgráfico mostrando as funções cumulativas
fig, (ax0, ax1) = plt.subplots(ncols=2, sharex=True, sharey=True, figsize=(10,5))
## A) via plt.step()
ax0.step(A, C, label='soma cumulativa')
ax0.scatter(A, B, label='Valores atuais')
ax0.set_ylabel('Y value')
ax0.legend(loc='upper right')
## B) via plt.plot()
ax1.plot(A, C, label='soma cumulativa')
ax1.scatter(A, B, label='Valores atuais')
ax1.legend(loc='upper right')
fig.text(0.5, 0.04, 'Número da amostra', ha='center', va='center')
fig.text(0.5, 0.95, 'Soma cumulativa de 10 amostras de uma distribuição normal aleatória', ha='center', va='center')
plt.show()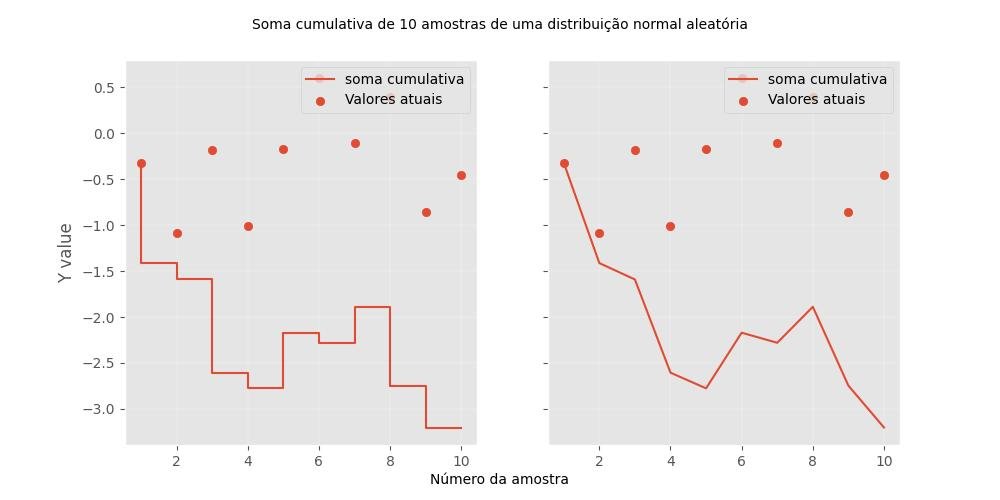
Contagem absoluta:
import numpy as np
import matplotlib.pyplot as plt
A = np.arange(1, 11)
B = np.random.randn(10) # 10 rand. values from a std. norm. distr.
plt.figure(figsize=(10,5))
plt.step(np.sort(B), A)
plt.ylabel('contagem de amostras')
plt.xlabel('valor x')
plt.title('Número de amostras em um determinado limite')
plt.show()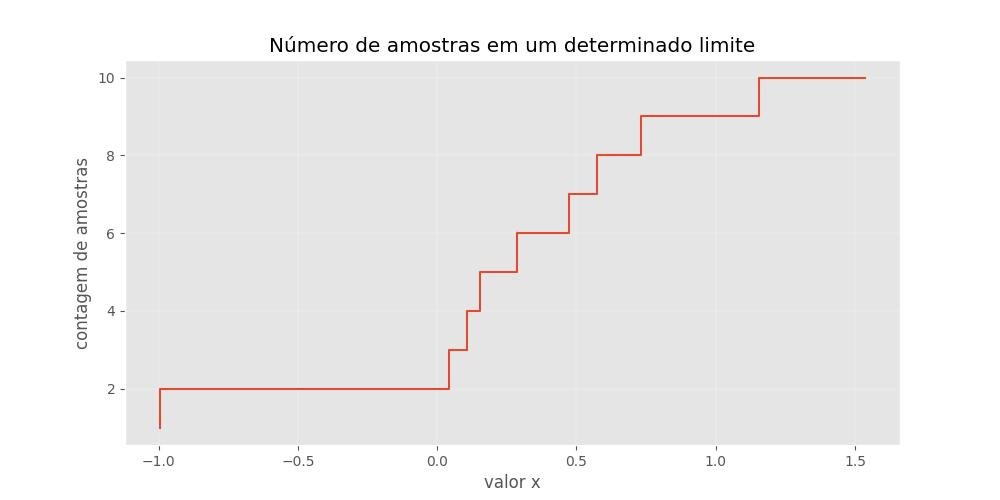
2.1.3.8.6 - Mapas de cores
Mais mapas de cores estão disponíveis em Scipy - Mapas de cores.
import numpy as np
import matplotlib.pyplot as plt
fig, (ax0, ax1) = plt.subplots(1,2, figsize=(14, 7))
amostras = range(1,16)
# Default Color Cycle
for i in amostras:
ax0.plot([0, 10], [0, i], label=i, lw=3)
# Mapa de cores Paired
colormap = plt.cm.Paired
plt.gca().set_prop_cycle(color=[colormap(i) for i in np.linspace(0, 0.9, len(amostras))])
for i in amostras:
ax1.plot([0, 10], [0, i], label=i, lw=3)
# Anotações
ax0.set_title('Ciclo de cores padrão')
ax1.set_title('Mapa de cores plt.cm.Paired')
ax0.legend(loc='upper left')
ax1.legend(loc='upper left')
plt.show()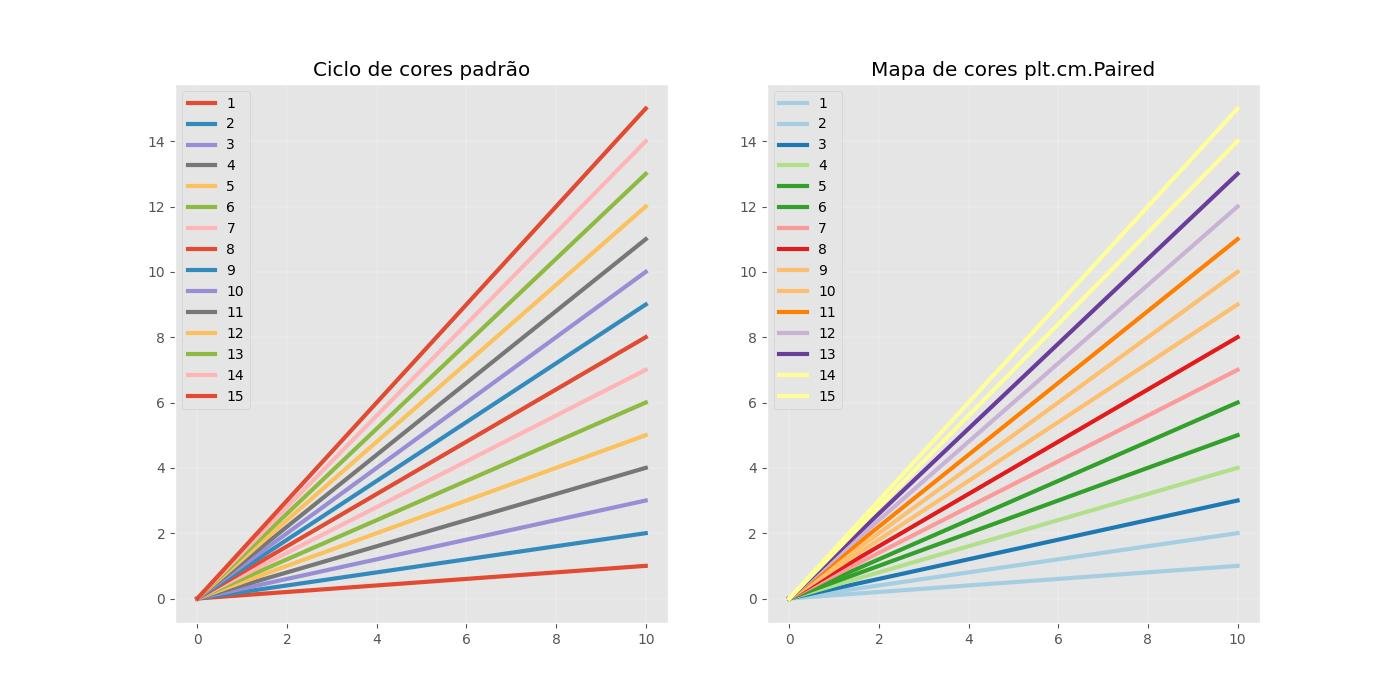
2.1.3.8.7 - Estilos de marcadores
import numpy as np
import matplotlib.pyplot as plt
marcadores = [
'.', # point
',', # pixel
'o', # circle
'v', # triangle down
'^', # triangle up
'<', # triangle_left
'>', # triangle_right
'1', # tri_down
'2', # tri_up
'3', # tri_left
'4', # tri_right
'8', # octagon
's', # square
'p', # pentagon
'*', # star
'h', # hexagon1
'H', # hexagon2
'+', # plus
'x', # x
'D', # diamond
'd', # thin_diamond
'|', # vline
]
plt.figure(figsize=(13, 10))
amostras = range(len(marcadores))
for i in amostras:
plt.plot([i-1, i, i+1], [i, i, i], label=marcadores[i], marker=marcadores[i], markersize=10)
# Anotações
plt.title('Estilos de marcadores Matplotlib', fontsize=20)
plt.ylim([-1, len(markers)+1])
plt.legend(loc='lower right')
plt.show()2.1.3.8.8 - Estilos de linha
import numpy as np
import matplotlib.pyplot as plt
estilos_linha = ['-.', '--', 'None', '-', ':']
plt.figure(figsize=(8, 5))
amostras = range(len(estilos_linha))
for i in amostras:
plt.plot(
[i-1, i, i+1], [i, i, i],
label='"%s"' %estilos_linha[i],
linestyle=estilos_linha[i],
lw=4
)
# Anotações
plt.title('Estilos de linha Matplotlib', fontsize=20)
plt.ylim([-1, len(estilos_linha)+1])
plt.legend(loc='lower right')
plt.show()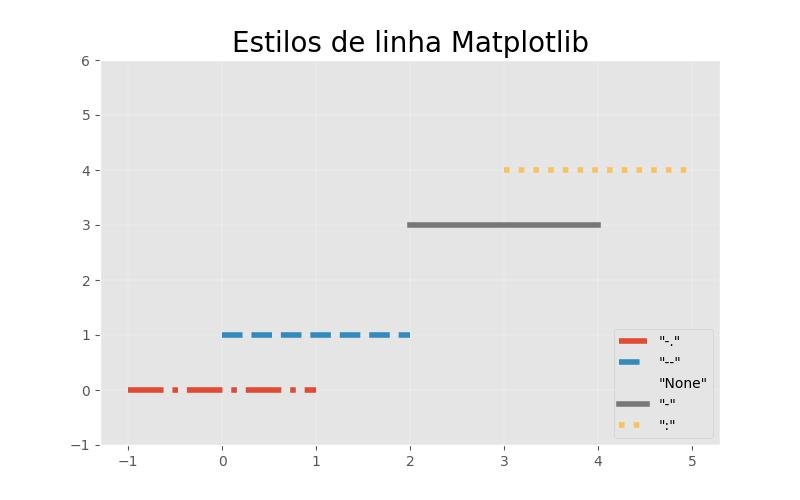
2.1.3.9 - Gráficos de dispersão
2.1.3.9.1 - Gráfico de dispersão básico
from matplotlib import pyplot as plt
import numpy as np
# Gerando um conjunto de dados Gaussion: criando vetores aleatórios,
# a partir da distribuição normal multivariada dada média e covariância.
mu_vec1 = np.array([0,0])
cov_mat1 = np.array([[2,0],[0,2]])
x1_amostras = np.random.multivariate_normal(mu_vec1, cov_mat1, 100)
x2_amostras = np.random.multivariate_normal(mu_vec1+0.2, cov_mat1+0.2, 100)
x3_amostras = np.random.multivariate_normal(mu_vec1+0.4, cov_mat1+0.4, 100)
# x1_amostras.shape -> (100, 2), 100 rows, 2 columns
plt.figure(figsize=(8,6))
plt.scatter(x1_amostras[:,0], x1_amostras[:,1], marker='x',
color='blue', alpha=0.7, label='x1 amostras')
plt.scatter(x2_amostras[:,0], x1_amostras[:,1], marker='o',
color='green', alpha=0.7, label='x2 amostras')
plt.scatter(x3_amostras[:,0], x1_amostras[:,1], marker='^',
color='red', alpha=0.7, label='x3 amostras')
plt.title('Gráfico de dispersão básico')
plt.ylabel('Variável X')
plt.xlabel('Variável Y')
plt.legend(loc='upper right')
plt.show()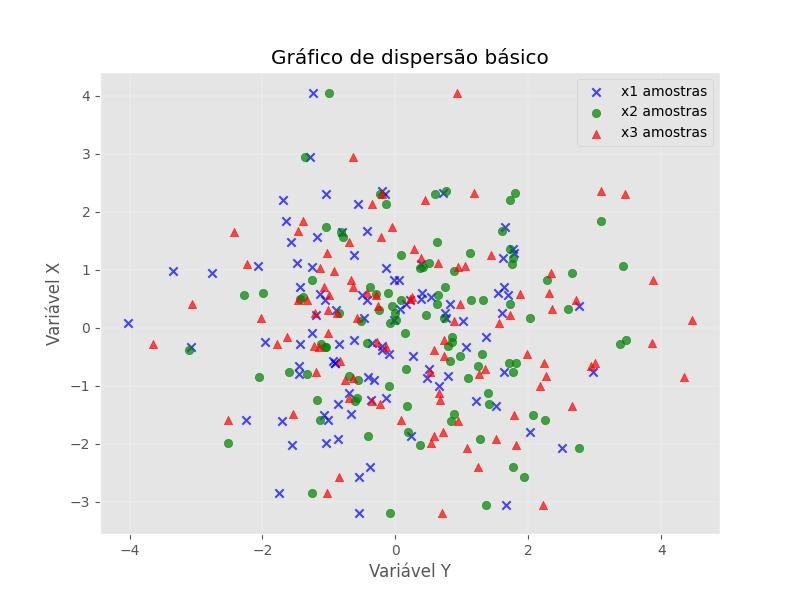
2.1.3.9.2 - Gráfico de dispersão com rótulos
import matplotlib.pyplot as plt
x_coords = [0.13, 0.22, 0.39, 0.59, 0.68, 0.74, 0.93]
y_coords = [0.75, 0.34, 0.44, 0.52, 0.80, 0.25, 0.55]
fig = plt.figure(figsize=(8,5))
plt.scatter(x_coords, y_coords, marker='s', s=50)
for x, y in zip(x_coords, y_coords):
plt.annotate(
'(%s, %s)' %(x, y),
xy=(x, y),
xytext=(0, -10),
textcoords='offset points',
ha='center',
va='top')
plt.xlim([0,1])
plt.ylim([0,1])
plt.show()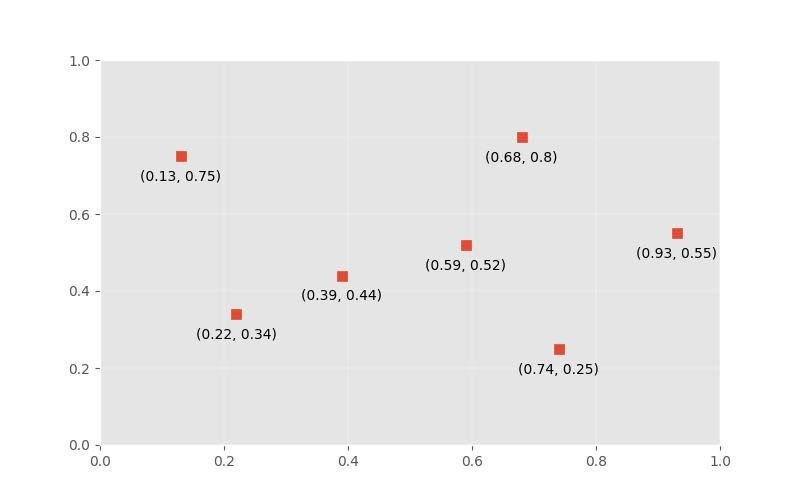
2.1.3.9.3 - Gráfico de dispersão de 2 classes com limite de decisão
# Classificação de 2 categorias com dados aleatórios de amostra 2D
# de uma distribuição normal multivariada
import numpy as np
from matplotlib import pyplot as plt
def decision_boundary(x_1):
""" Calculates the x_2 value for plotting the decision boundary."""
return 4 - np.sqrt(-x_1**2 + 4*x_1 + 6 + np.log(16))
# Gerando um conjunto de dados Gaussion: criando vetores aleatórios a partir
# da distribuição normal multivariada dada média e covariância
mu_vec1 = np.array([0,0])
cov_mat1 = np.array([[2,0],[0,2]])
x1_amostras = np.random.multivariate_normal(mu_vec1, cov_mat1, 100)
mu_vec1 = mu_vec1.reshape(1,2).T # to 1-col vector
mu_vec2 = np.array([1,2])
cov_mat2 = np.array([[1,0],[0,1]])
x2_amostras = np.random.multivariate_normal(mu_vec2, cov_mat2, 100)
mu_vec2 = mu_vec2.reshape(1,2).T # to 1-col vector
# Gráfico de dispersão principal e anotação do gráfico
f, ax = plt.subplots(figsize=(7, 7))
ax.scatter(x1_amostras[:,0], x1_amostras[:,1], marker='o', color='green', s=40, alpha=0.5)
ax.scatter(x2_amostras[:,0], x2_amostras[:,1], marker='^', color='blue', s=40, alpha=0.5)
plt.legend(['Class1 (w1)', 'Class2 (w2)'], loc='upper right')
plt.title('Densidades de 2 classes com 25 padrões aleatórios bivariados cada')
plt.ylabel('x2')
plt.xlabel('x1')
ftext = 'p(x|w1) ~ N(mu1=(0,0)^t, cov1=I)\np(x|w2) ~ N(mu2=(1,1)^t, cov2=I)'
plt.figtext(.15,.8, ftext, fontsize=11, ha='left')
# Adicionando limite de decisão ao gráfico
x_1 = np.arange(-5, 5, 0.1)
bound = decision_boundary(x_1)
plt.plot(x_1, bound, 'r--', lw=3)
x_vec = np.linspace(*ax.get_xlim())
x_1 = np.arange(0, 100, 0.05)
plt.show()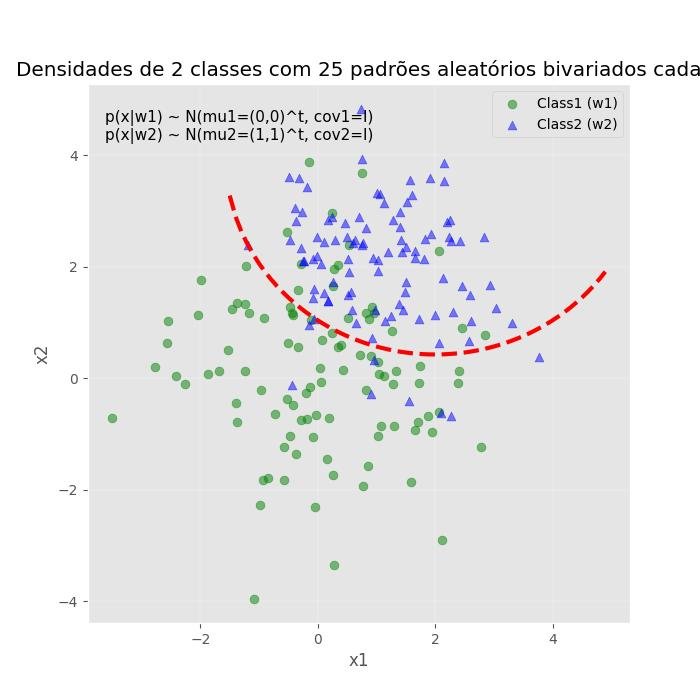
2.1.3.9.4 - Aumentando o tamanho do ponto com a distância da origem
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(8,6))
# Gerando um conjunto de dados Gaussion:
# criando vetores aleatórios a partir da distribuição normal multivariada
# dada média e covariância
mu_vec1 = np.array([0,0])
cov_mat1 = np.array([[1,0],[0,1]])
X = np.random.multivariate_normal(mu_vec1, cov_mat1, 500)
R = X**2
R_sum = R.sum(axis=1)
plt.scatter(X[:, 0], X[:, 1],
color='gray',
marker='o',
s=32. * R_sum,
edgecolor='black',
alpha=0.5)
plt.show()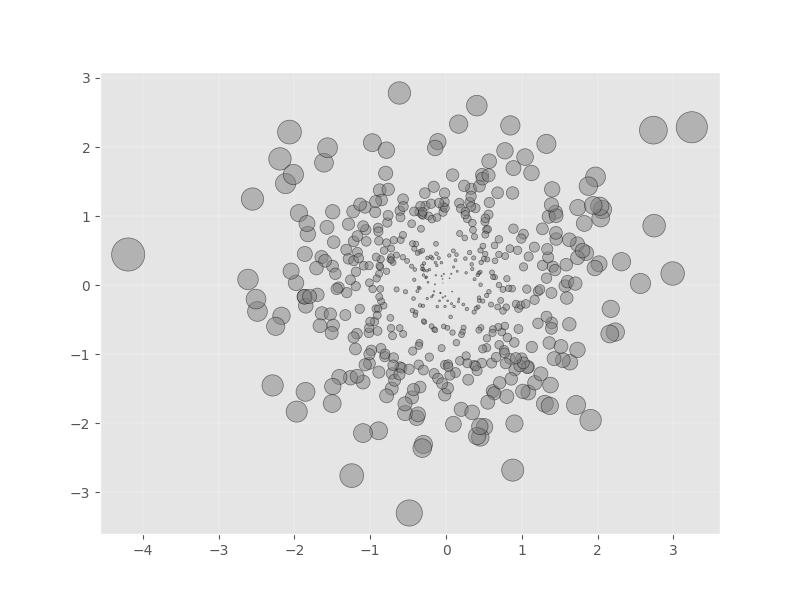
2.1.3.10 - Gráficos Especiais
2.1.3.10.1 - gráfico de pizza básico
from matplotlib import pyplot as plt
import numpy as np
plt.pie(
(10,5),
labels=('spam','ham'),
shadow=True,
colors=('yellowgreen', 'lightskyblue'),
explode=(0,0.15), # space between slices
startangle=90, # rotate conter-clockwise by 90 degrees
autopct='%1.1f%%',# display fraction as percentage
)
plt.legend(fancybox=True)
plt.axis('equal') # plot pyplot as circle
plt.tight_layout()
plt.show()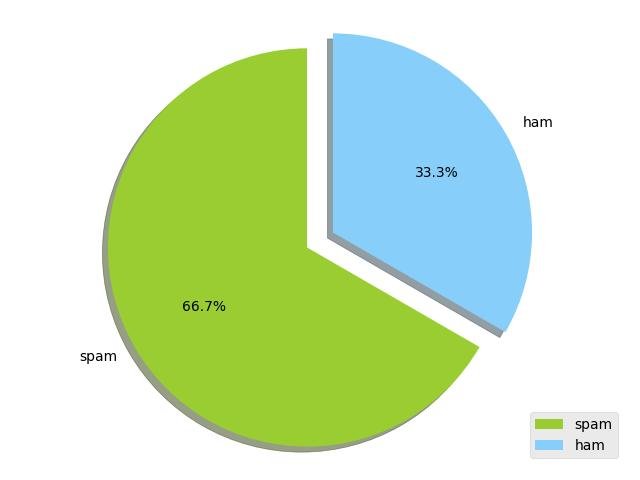
2.1.3.10.2 - Triangulação básica
from matplotlib import pyplot as plt
import matplotlib.tri as tri
import numpy as np
rand_data = np.random.randn(50, 2)
triangulacao = tri.Triangulation(rand_data[:,0], rand_data[:,1])
plt.triplot(triangulacao)
plt.show()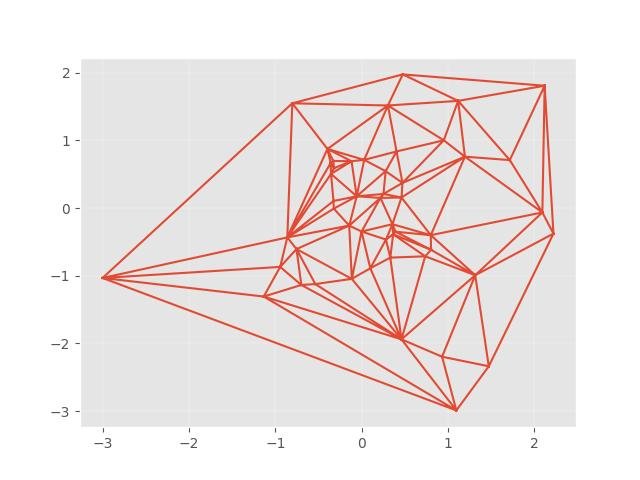
2.1.3.10.3 - Plotagens estilo xkcd
import matplotlib.pyplot as plt
x = [1, 2, 3]
y_1 = [50, 60, 70]
y_2 = [20, 30, 40]
with plt.xkcd():
plt.plot(x, y_1, marker='x')
plt.plot(x, y_2, marker='^')
plt.xlim([0, len(x)+1])
plt.ylim([0, max(y_1+y_2) + 10])
plt.xlabel('x-axis label')
plt.ylabel('y-axis label')
plt.title('Gráfico de linha simples')
plt.legend(['amostra 1', 'amostra 2'], loc='upper left')
plt.show()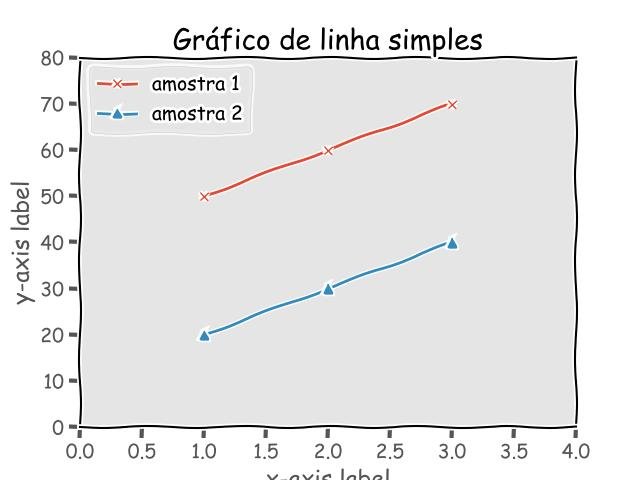
import numpy as np
import random
from matplotlib import pyplot as plt
data = np.random.normal(0, 20, 1000)
bins = np.arange(-100, 100, 5) # tamanho fixo da caixa
with plt.xkcd():
plt.xlim([min(data)-5, max(data)+5])
plt.hist(data, bins=bins, alpha=0.5)
plt.title('Dados gaussianos aleatórios (tamanho fixo da caixa)')
plt.xlabel('variável X (tamanho da caixa = 5)')
plt.ylabel('contagem')
plt.show()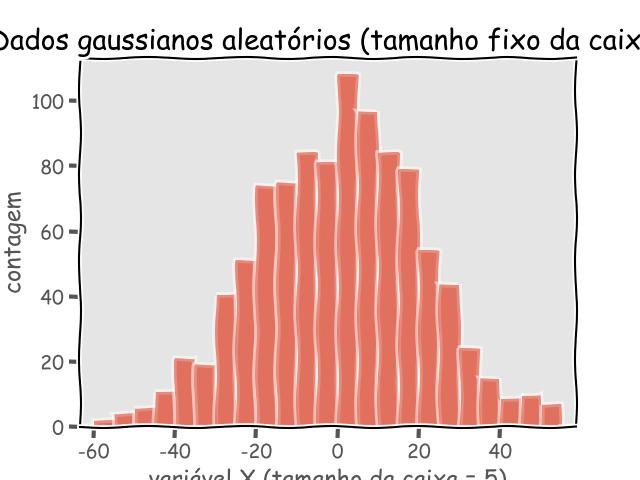
from matplotlib import pyplot as plt
import numpy as np
with plt.xkcd():
X = np.random.random_integers(1,5,5) # 5 random integers within 1-5
cols = ['b', 'g', 'r', 'y', 'm']
plt.pie(X, colors=cols)
plt.legend(X)
plt.show()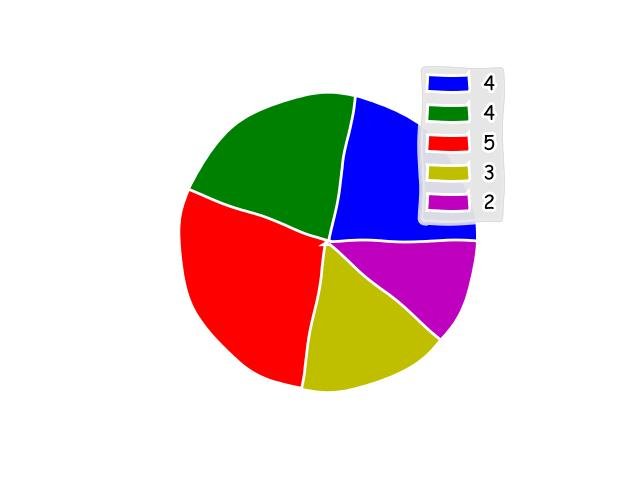
2.1.4 - Galeria Seaborn
2.1.4.1 - Quarteto de Anscombe
import seaborn as sns
import matplotlib.pyplot as plt
sns.set_theme(style="ticks")
# Carrega o conjunto de dados do quarteto de Anscombe
df = sns.load_dataset("anscombe")
# Mostra os resultados de uma regressão linear dentro de cada conjunto de dados
fig = sns.lmplot(
data=df, x="x", y="y", col="dataset", hue="dataset",
col_wrap=2, palette="muted", ci=None,
height=4, scatter_kws={"s": 50, "alpha": 1}
)
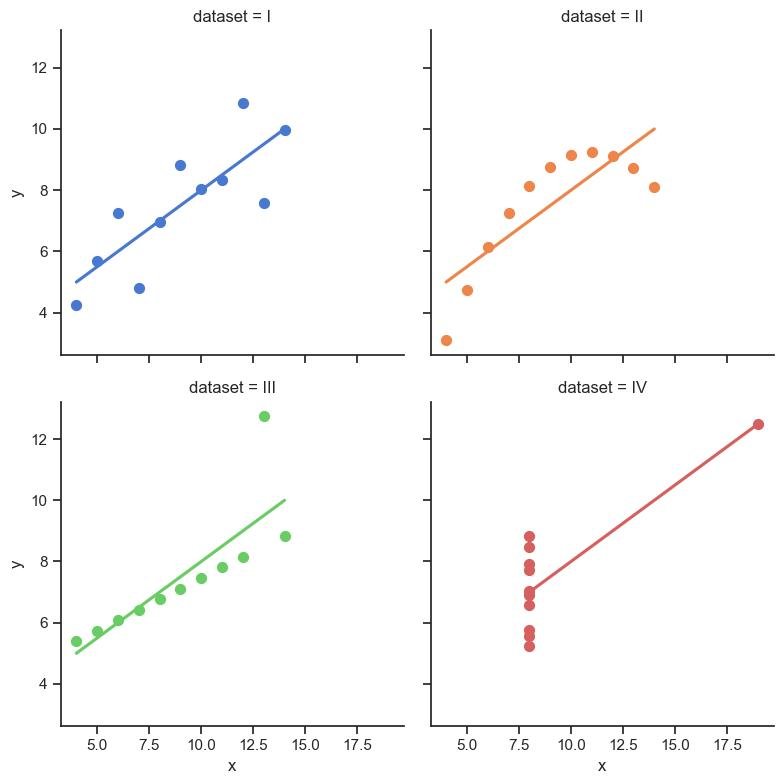
2.1.4.2 - Gráfico de dispersão com semântica múltipla
import seaborn as sns
import matplotlib.pyplot as plt
sns.set_theme(style="whitegrid")
# carregar o exemplo de dados de diamantes
diamonds = sns.load_dataset("diamonds")
# Desenhe um gráfico de dispersão ao atribuir cores e tamanhos de pontos a diferentes variáveis no conjunto de dados
fig, ax = plt.subplots(figsize=(6.5, 6.5))
sns.despine(fig, left=True, bottom=True)
clarity_ranking = ["I1", "SI2", "SI1", "VS2", "VS1", "VVS2", "VVS1", "IF"]
sns.scatterplot(
x="carat", y="price",
hue="clarity", size="depth",
palette="ch:r=-.2,d=.3_r",
hue_order=clarity_ranking,
sizes=(1, 8), linewidth=0,
data=diamonds, ax=ax)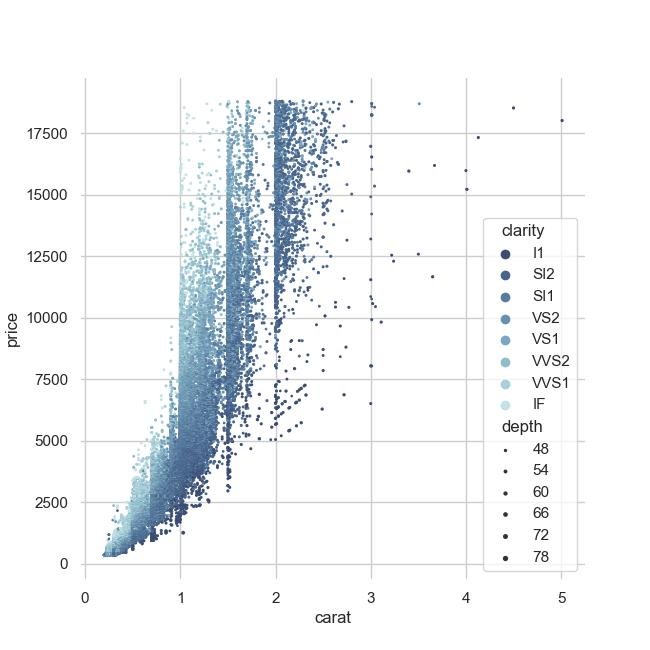
2.1.4.3 - Gráfico de série temporal com bandas de erro
import seaborn as sns
sns.set_theme(style="darkgrid")
# Load an example dataset with long-form data
fmri = sns.load_dataset("fmri")
# Plot the responses for different events and regions
fig = sns.lineplot(
x="timepoint", y="signal",
hue="region", style="event",
data=fmri)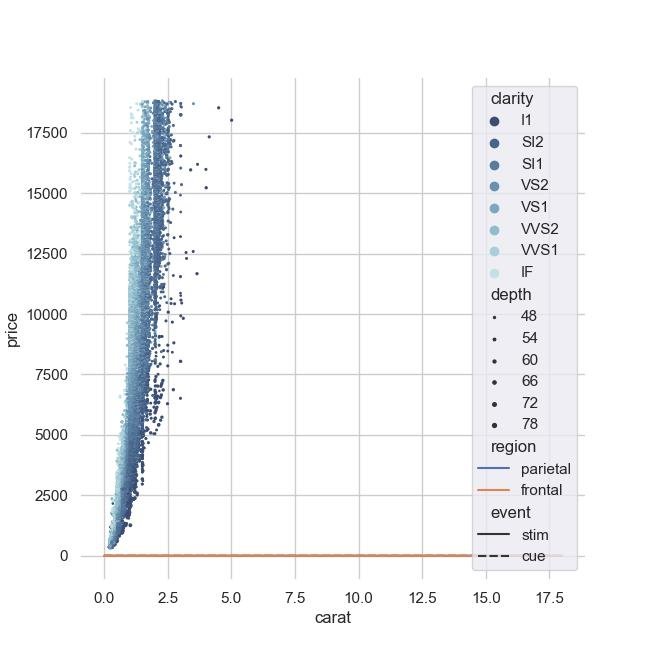
2.1.4.4 - Facetando histogramas por subconjuntos de dados
import seaborn as sns
sns.set_theme(style="darkgrid")
df = sns.load_dataset("penguins")
fig = sns.displot(
df, x="flipper_length_mm", col="species", row="sex",
binwidth=3, height=3, facet_kws=dict(margin_titles=True),
)
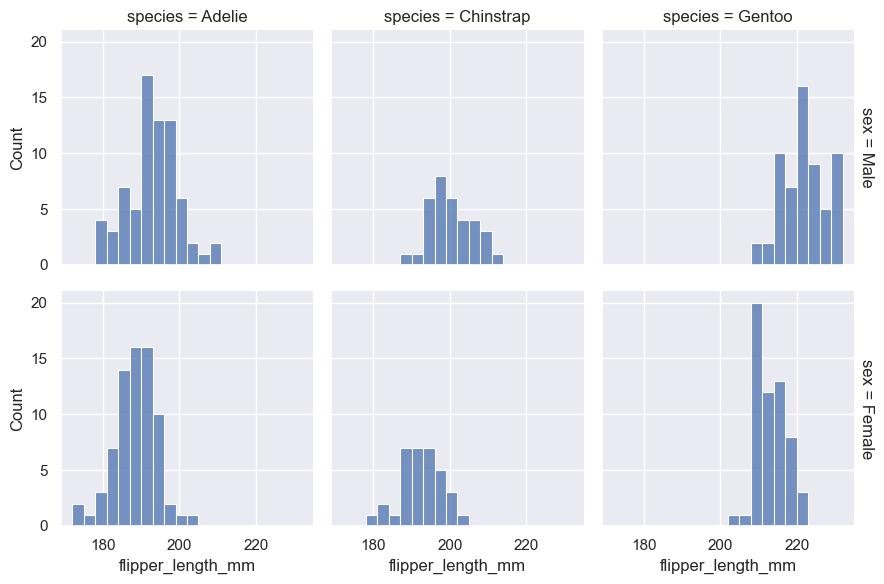
2.1.4.5 - Gráficos de linha em várias facetas
import seaborn as sns
sns.set_theme(style="ticks")
dots = sns.load_dataset("dots")
# Defina a paleta como uma lista para especificar valores exatos
palette = sns.color_palette("rocket_r")
# Traçar as linhas em duas facetas
fig = sns.relplot(
data=dots,
x="time", y="firing_rate",
hue="coherence", size="choice", col="align",
kind="line", size_order=["T1", "T2"], palette=palette,
height=5, aspect=.75, facet_kws=dict(sharex=False),
)
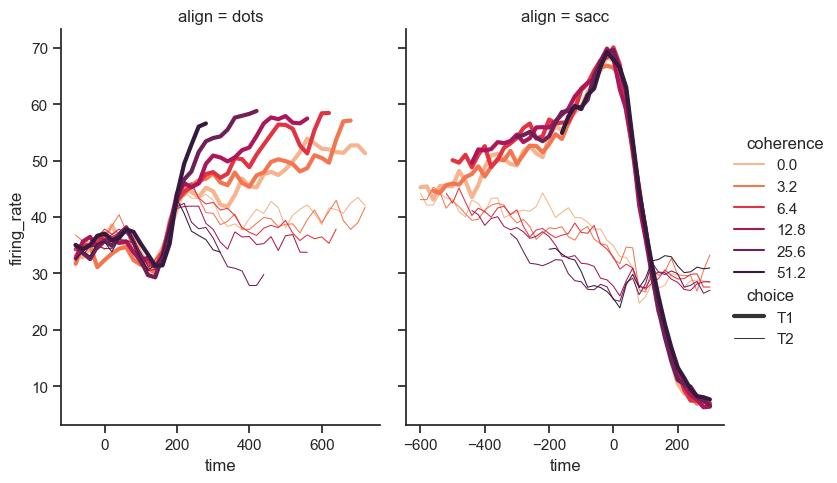
2.1.4.6 - Gráficos de barras agrupados
import seaborn as sns
sns.set_theme(style="whitegrid")
penguins = sns.load_dataset("penguins")
# Draw a nested barplot by species and sex
fig = sns.catplot(
data=penguins, kind="bar",
x="species", y="body_mass_g", hue="sex",
palette="dark", alpha=.6, height=6
)
fig.despine(left=True)
fig.set_axis_labels("", "Body mass (g)")
fig.legend.set_title("")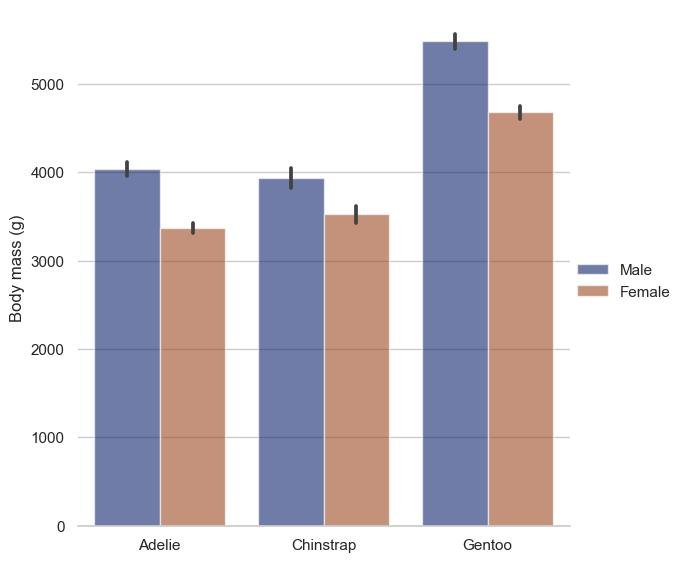
2.1.4.7 - Boxplots agrupados
import seaborn as sns
sns.set_theme(style="ticks", palette="pastel")
# Load the example tips dataset
tips = sns.load_dataset("tips")
# Desenhe um boxplot aninhado para mostrar contas por dia e hora
fig = sns.boxplot(x="day", y="total_bill",
hue="smoker", palette=["m", "g"],
data=tips)
sns.despine(offset=10, trim=True)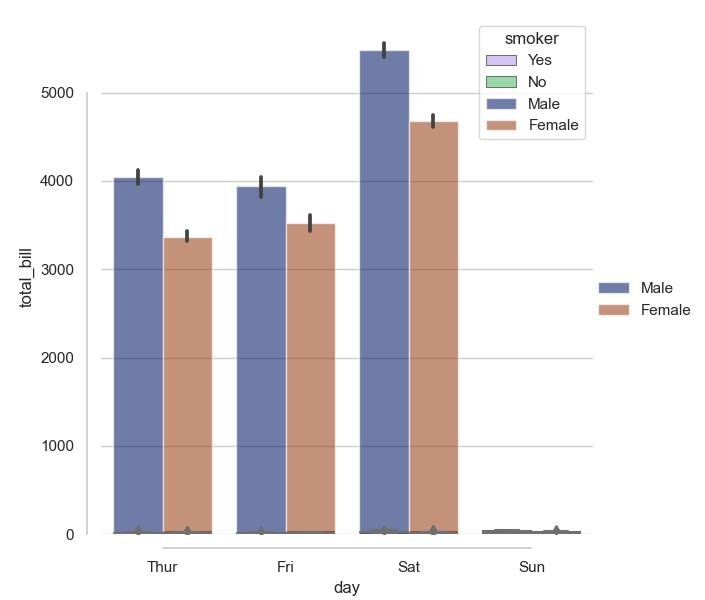
2.1.4.8 - Violinplots agrupados com violinos divididos
import seaborn as sns
sns.set_theme(style="whitegrid")
# Carregar o conjunto de dados de dicas de exemplo
tips = sns.load_dataset("tips")
# Desenhe um gráfico de violino aninhado e divida os violinos para uma comparação mais fácil
fig = sns.violinplot(data=tips, x="day", y="total_bill", hue="smoker",
split=True, inner="quart", linewidth=1,
palette={"Yes": "b", "No": ".85"})
sns.despine(left=True)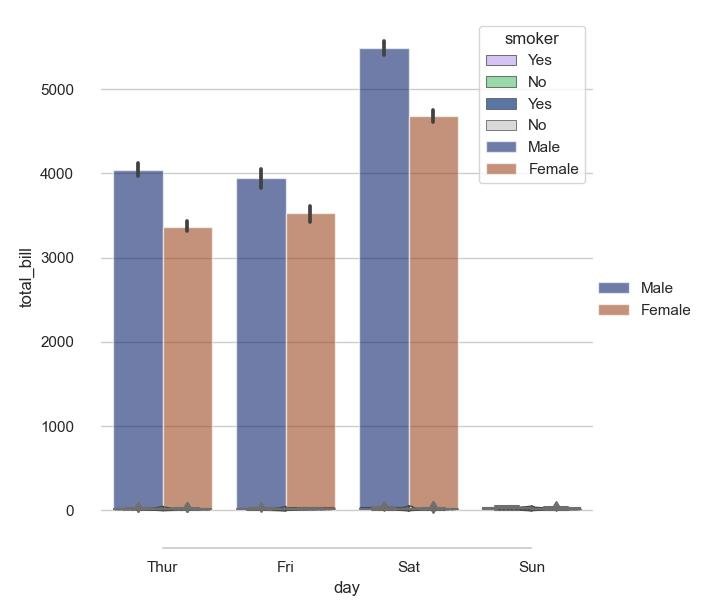
2.1.4.9 - Mapa de calor do gráfico de distribuição
import seaborn as sns
sns.set_theme(style="whitegrid")
# Carregue o conjunto de dados das redes cerebrais, selecione o subconjunto e recolha o índice múltiplo
df = sns.load_dataset("brain_networks", header=[0, 1, 2], index_col=0)
used_networks = [1, 5, 6, 7, 8, 12, 13, 17]
used_columns = (df.columns
.get_level_values("network")
.astype(int)
.isin(used_networks))
df = df.loc[:, used_columns]
df.columns = df.columns.map("-".join)
# Calcular uma matriz de correlação e converter para formato longo
corr_mat = df.corr().stack().reset_index(name="correlation")
# Desenhe cada célula como um ponto de dispersão com tamanho e cor variados
fig = sns.relplot(
data=corr_mat,
x="level_0", y="level_1", hue="correlation", size="correlation",
palette="vlag", hue_norm=(-1, 1), edgecolor=".7",
height=10, sizes=(50, 250), size_norm=(-.2, .8),
)
# Ajuste a figura para finalizar
fig.set(xlabel="", ylabel="", aspect="equal")
fig.despine(left=True, bottom=True)
fig.ax.margins(.02)
for label in fig.ax.get_xticklabels():
label.set_rotation(90)
for artist in fig.legend.legendHandles:
artist.set_edgecolor(".7")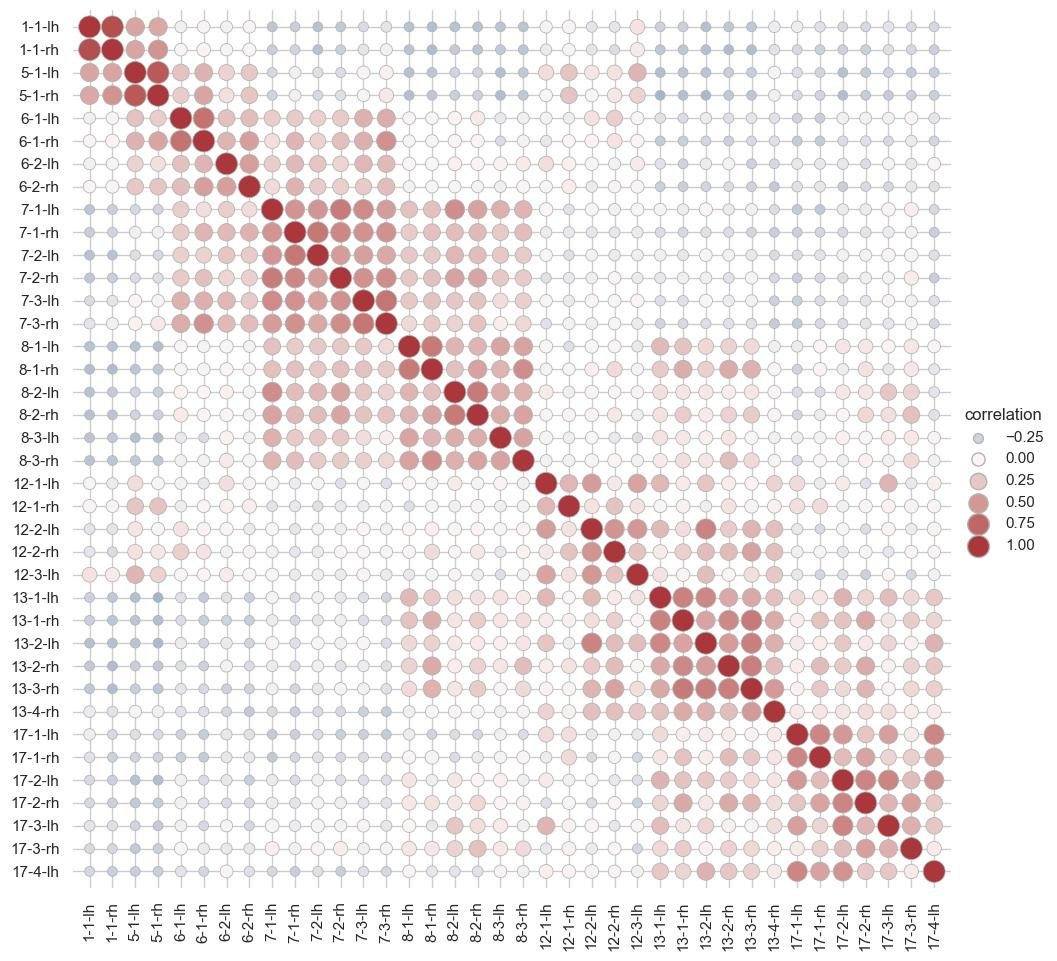
2.1.4.10 - Gráfico Hexbin com distribuições marginais
import numpy as np
import seaborn as sns
sns.set_theme(style="ticks")
rs = np.random.RandomState(11)
x = rs.gamma(2, size=1000)
y = -.5 * x + rs.normal(size=1000)
fig = sns.jointplot(x=x, y=y, kind="hex", color="#4CB391")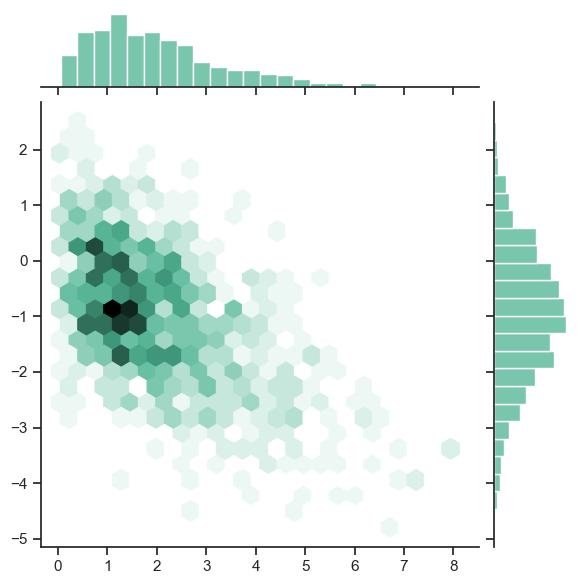
2.1.4.11 - Histograma empilhado em escala logarítmica
import seaborn as sns
import matplotlib as mpl
import matplotlib.pyplot as plt
sns.set_theme(style="ticks")
diamonds = sns.load_dataset("diamonds")
fig, ax = plt.subplots(figsize=(7, 5))
sns.despine(fig)
sns.histplot(
diamonds,
x="price", hue="cut",
multiple="stack",
palette="light:m_r",
edgecolor=".3",
linewidth=.5,
log_scale=True,
)
ax.xaxis.set_major_formatter(mpl.ticker.ScalarFormatter())
ax.set_xticks([500, 1000, 2000, 5000, 10000])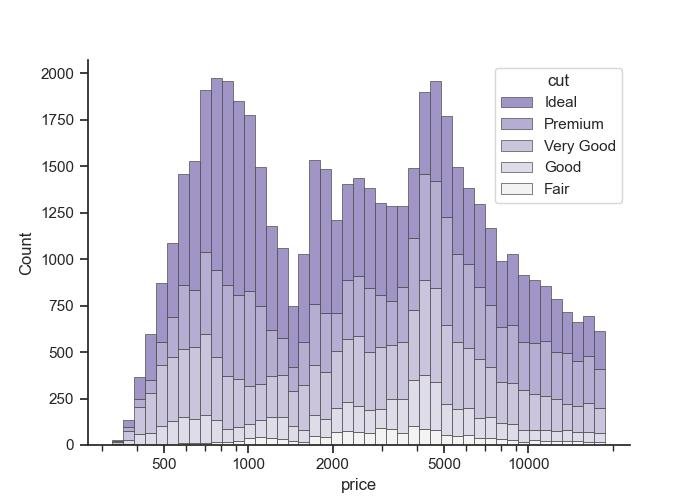
2.1.4.12 - Boxplot horizontal com observações
import seaborn as sns
import matplotlib.pyplot as plt
sns.set_theme(style="ticks")
# Inicialize a figura com um eixo x logarítmico
fig, ax = plt.subplots(figsize=(7, 6))
ax.set_xscale("log")
# Carregar o conjunto de dados de planetas de exemplo
planets = sns.load_dataset("planets")
# Plote o período orbital com caixas horizontais
sns.boxplot(x="distance", y="method", data=planets,
whis=[0, 100], width=.6, palette="vlag")
# Adicione pontos para mostrar cada observação
sns.stripplot(x="distance", y="method", data=planets,
size=4, color=".3", linewidth=0)
# Ajuste a apresentação visual
ax.xaxis.grid(True)
ax.set(ylabel="")
sns.despine(trim=True, left=True)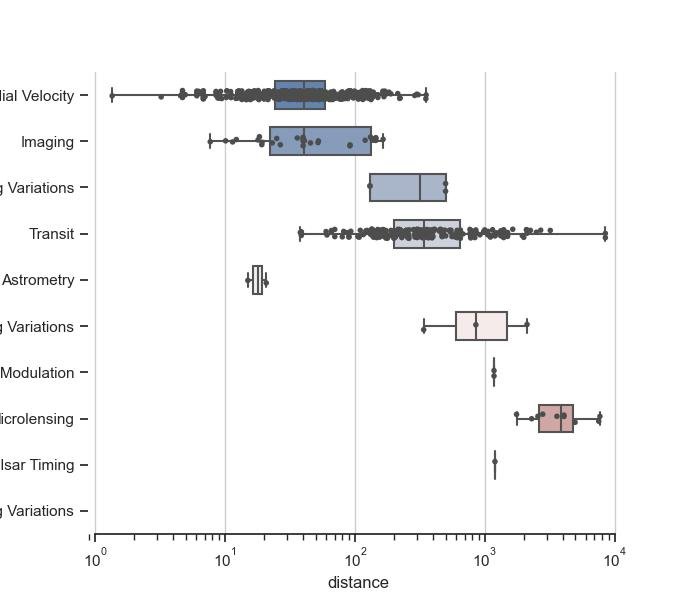
2.1.4.13 - Histogramas articulares e marginais
import seaborn as sns
sns.set_theme(style="ticks")
# Carregue o conjunto de dados dos planetas e inicialize a figura
planetas = sns.load_dataset("planets")
fig = sns.JointGrid(data=planetas, x="year", y="distance", marginal_ticks=True)
# Definir uma escala de log no eixo y
fig.ax_joint.set(yscale="log")
# Create an inset legend for the histogram colorbar
cax = fig.figure.add_axes([.15, .55, .02, .2])
# Adicione os gráficos de histogramas articulares e marginais
fig.plot_joint(
sns.histplot, discrete=(True, False),
cmap="light:#03012d", pmax=.8, cbar=True, cbar_ax=cax
)
fig.plot_marginals(sns.histplot, element="step", color="#03012d")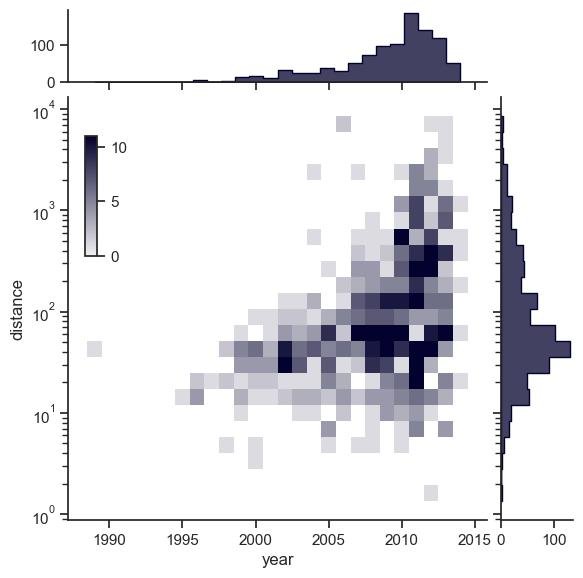
2.1.4.14 - Estimativa de densidade de kernel conjunta
import seaborn as sns
sns.set_theme(style="ticks")
# Carregar o conjunto de dados de pinguins
penguins = sns.load_dataset("penguins")
# Mostrar a distribuição conjunta usando estimativa de densidade de kernel
fig = sns.jointplot(
data=penguins,
x="bill_length_mm", y="bill_depth_mm", hue="species",
kind="kde",
)
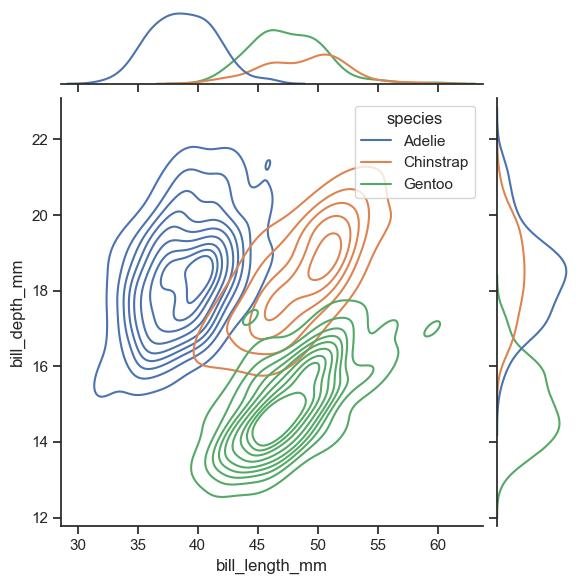
2.1.4.15 - Densidades sobrepostas ('grifo gráfico')
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
sns.set_theme(style="white", rc={"axes.facecolor": (0, 0, 0, 0)})
# Create the data
rs = np.random.RandomState(1979)
x = rs.randn(500)
g = np.tile(list("ABCDEFGHIJ"), 50)
df = pd.DataFrame(dict(x=x, g=g))
m = df.g.map(ord)
df["x"] += m
# Inicialize o objeto FacetGrid
pal = sns.cubehelix_palette(10, rot=-.25, light=.7)
fig = sns.FacetGrid(df, row="g", hue="g", aspect=15, height=.5, palette=pal)
# Desenhe as densidades em poucos passos
fig.map(sns.kdeplot, "x",
bw_adjust=.5, clip_on=False,
fill=True, alpha=1, linewidth=1.5)
fig.map(sns.kdeplot, "x", clip_on=False, color="w", lw=2, bw_adjust=.5)
# Passando color=None para refline() usa o mapeamento de matiz
fig.refline(y=0, linewidth=2, linestyle="-", color=None, clip_on=False)
# Defina e use uma função simples para rotular o gráfico nas coordenadas dos eixos
def label(x, color, label):
ax = plt.gca()
ax.text(0, .2, label, fontweight="bold", color=color,
ha="left", va="center", transform=ax.transAxes)
fig.map(label, "x")
# Defina as subtramas para se sobrepor
fig.figure.subplots_adjust(hspace=-.25)
# Remova os detalhes dos eixos que não funcionam bem com a sobreposição
fig.set_titles("")
fig.set(yticks=[], ylabel="")
fig.despine(bottom=True, left=True)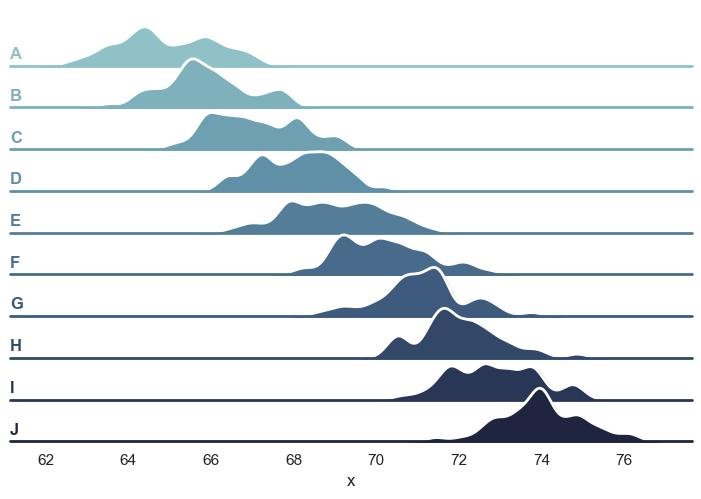
2.1.4.16 - Traçando grandes distribuições
import seaborn as sns
sns.set_theme(style="whitegrid")
diamonds = sns.load_dataset("diamonds")
clarity_ranking = ["I1", "SI2", "SI1", "VS2", "VS1", "VVS2", "VVS1", "IF"]
fig = sns.boxenplot(
x="clarity", y="carat",
color="b", order=clarity_ranking,
scale="linear", data=diamonds)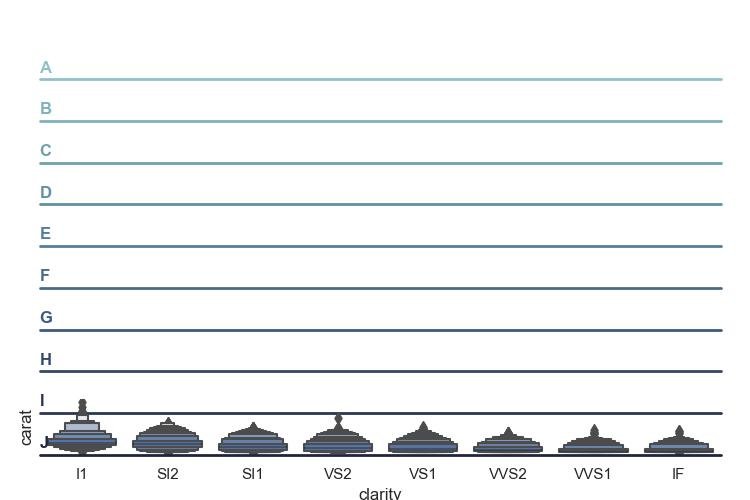
2.1.4.17 - Gráfico bivariado com vários elementos
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
sns.set_theme(style="dark")
# Simular dados de um gaussiano bivariado
n = 10000
mean = [0, 0]
cov = [(2, .4), (.4, .2)]
rng = np.random.RandomState(0)
x, y = rng.multivariate_normal(mean, cov, n).T
# Desenhe um histograma combinado e um gráfico de dispersão com contornos de densidade
fig, ax = plt.subplots(figsize=(6, 6))
sns.scatterplot(x=x, y=y, s=5, color=".15")
sns.histplot(x=x, y=y, bins=50, pthresh=.1, cmap="mako")
sns.kdeplot(x=x, y=y, levels=5, color="w", linewidths=1)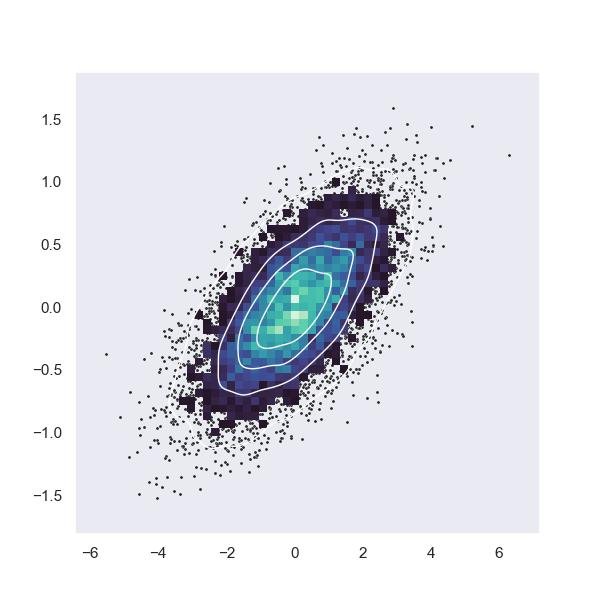
2.1.4.18 - Regressão logística facetada
import seaborn as sns
sns.set_theme(style="darkgrid")
# Load the example Titanic dataset
df = sns.load_dataset("titanic")
# Make a custom palette with gendered colors
pal = dict(male="#6495ED", female="#F08080")
# Mostrar a probabilidade de sobrevivência em função da idade e do sexo
fig = sns.lmplot(x="age", y="survived", col="sex", hue="sex", data=df,
palette=pal, y_jitter=.02, logistic=True, truncate=False)
fig.set(xlim=(0, 80), ylim=(-.05, 1.05))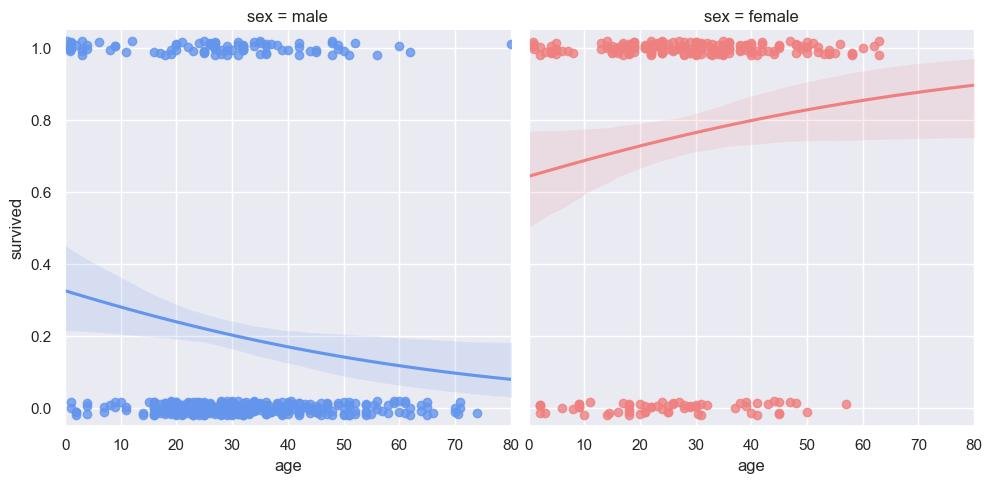
2.1.4.19 - Plotando em um grande número de facetas
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
sns.set_theme(style="ticks")
# Crie um conjunto de dados com muitos passeios aleatórios curtos
rs = np.random.RandomState(4)
pos = rs.randint(-1, 2, (20, 5)).cumsum(axis=1)
pos -= pos[:, 0, np.newaxis]
step = np.tile(range(5), 20)
walk = np.repeat(range(20), 5)
df = pd.DataFrame(
np.c_[pos.flat, step, walk],
columns=["position", "step", "walk"])
# Iniciar uma grade de gráficos com um Axes para cada
fig = sns.FacetGrid(
df, col="walk", hue="walk", palette="tab20c",
col_wrap=4, height=1.5)
# Desenhe uma linha horizontal para mostrar o ponto de partida
fig.refline(y=0, linestyle=":")
# Desenhe um gráfico de linha para mostrar a trajetória de cada caminhada aleatória
fig.map(plt.plot, "step", "position", marker="o")
# Ajuste as posições e rótulos dos ticks
fig.set(xticks=np.arange(5), yticks=[-3, 3],
xlim=(-.5, 4.5), ylim=(-3.5, 3.5))
# Ajuste a disposição das parcelas
fig.fig.tight_layout(w_pad=1)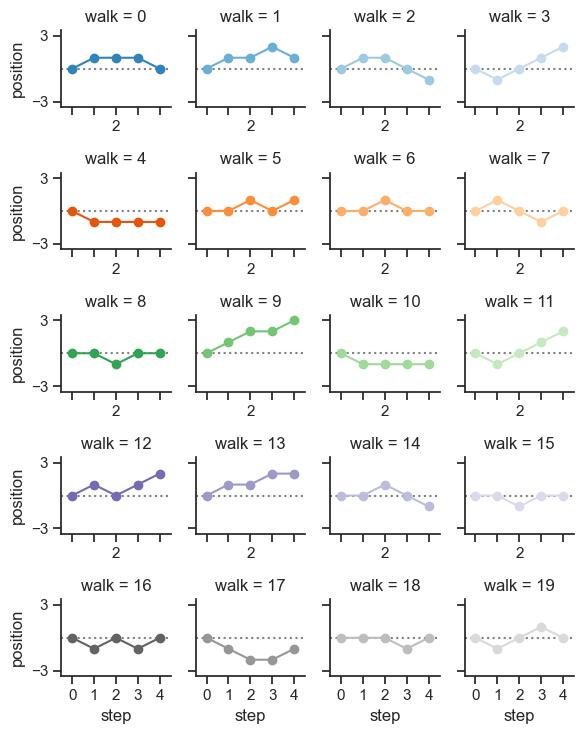
2.1.4.20 - Traçando uma matriz de correlação diagonal
from string import ascii_letters
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
sns.set_theme(style="white")
# Gerar um grande conjunto de dados aleatório
rs = np.random.RandomState(33)
d = pd.DataFrame(
data=rs.normal(size=(100, 26)),
columns=list(ascii_letters[26:]))
# Calcular a matriz de correlação
corr = d.corr()
# Gere uma máscara para o triângulo superior
mask = np.triu(np.ones_like(corr, dtype=bool))
# Configurar a figura matplotlib
fig, ax = plt.subplots(figsize=(11, 9))
# Gere um mapa de cores divergente personalizado
cmap = sns.diverging_palette(230, 20, as_cmap=True)
# Desenhe o mapa de calor com a máscara e a proporção correta
sns.heatmap(
corr, mask=mask, cmap=cmap, vmax=.3, center=0,
square=True, linewidths=.5, cbar_kws={"shrink": .5})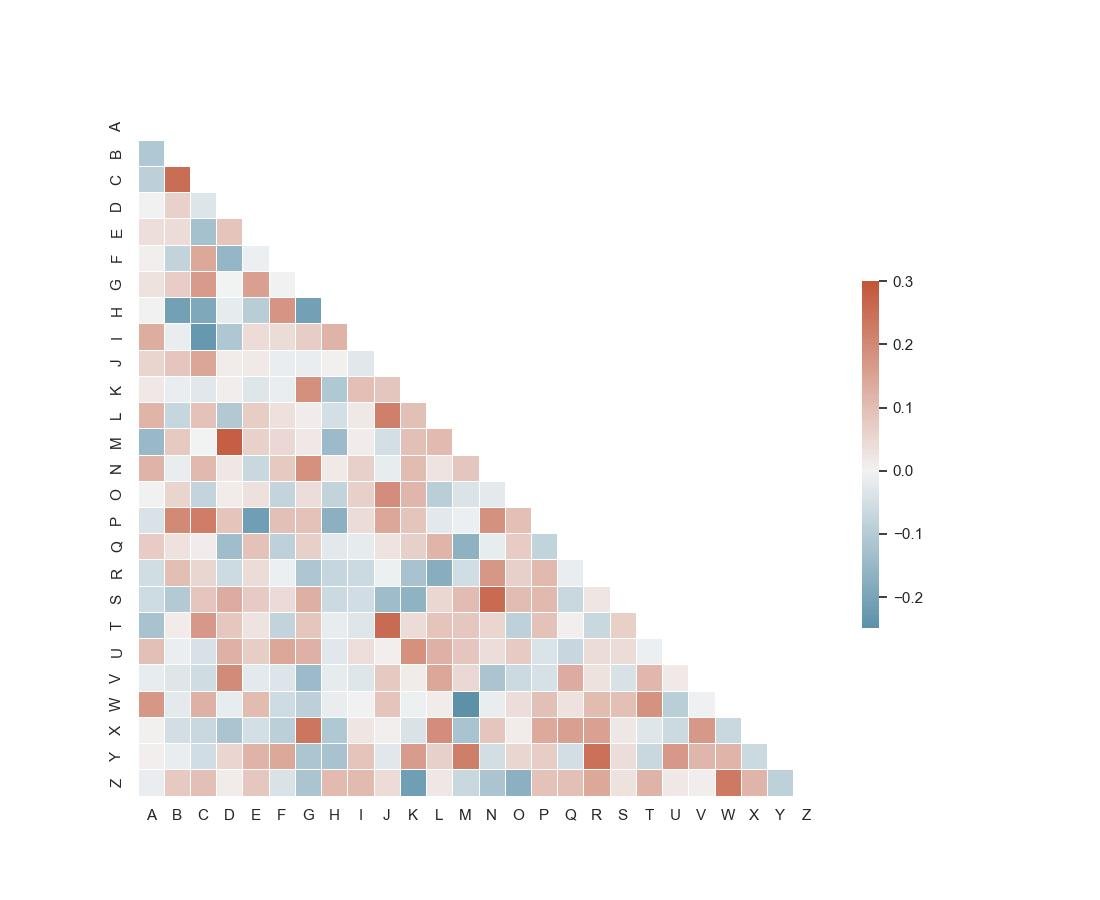
2.1.4.21 - Gráfico de dispersão com marcações marginais
import seaborn as sns
sns.set_theme(style="white", color_codes=True)
mpg = sns.load_dataset("mpg")
# Use o JointGrid diretamente para desenhar um gráfico personalizado
fig = sns.JointGrid(data=mpg, x="mpg", y="acceleration", space=0, ratio=17)
fig.plot_joint(
sns.scatterplot, size=mpg["horsepower"], sizes=(30, 120),
color="g", alpha=.6, legend=False)
fig.plot_marginals(sns.rugplot, height=1, color="g", alpha=.6)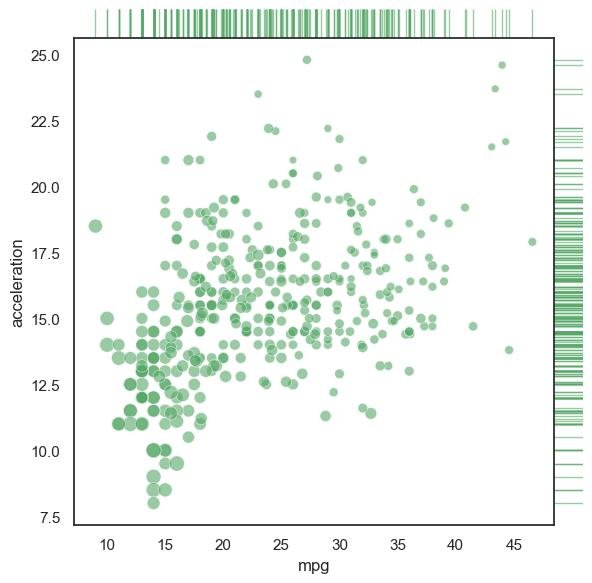
2.1.4.22 - Múltiplos gráficos bivariados do KDE
import seaborn as sns
import matplotlib.pyplot as plt
sns.set_theme(style="darkgrid")
iris = sns.load_dataset("iris")
# Configure a figura
fig, ax = plt.subplots(figsize=(8, 8))
ax.set_aspect("equal")
# Desenhe um gráfico de contorno para representar cada densidade bivariada
sns.kdeplot(
data=iris.query("species != 'versicolor'"),
x="sepal_width",
y="sepal_length",
hue="species",
thresh=.1,
)
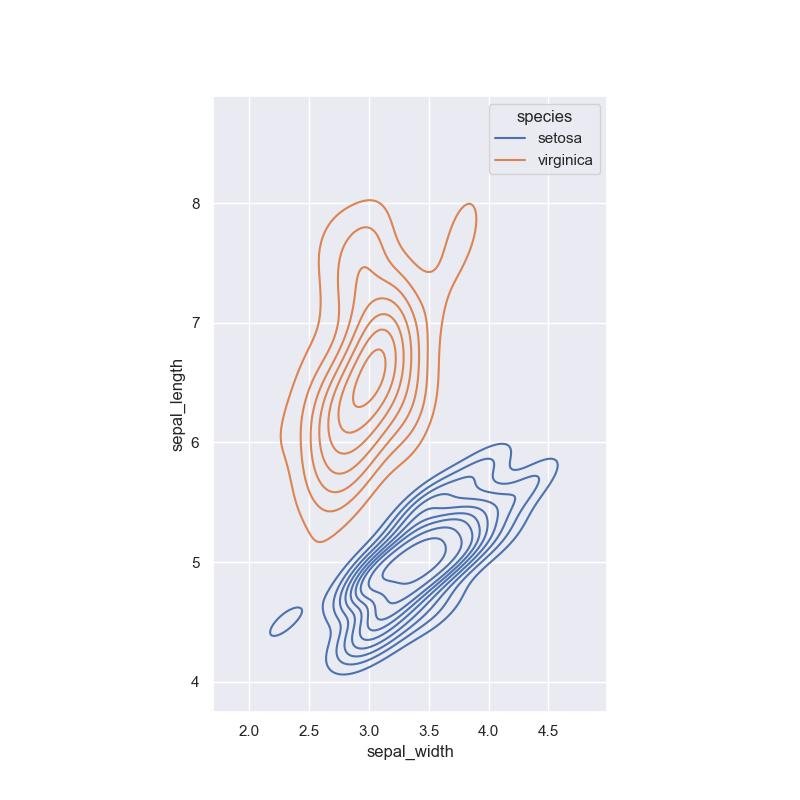
2.1.4.23 - Estimativa de densidade de kernel condicional
import seaborn as sns
sns.set_theme(style="whitegrid")
# Desenhe um gráfico de contorno para representar cada densidade bivariada
diamonds = sns.load_dataset("diamonds")
# Traçar a distribuição de classificações de clareza, condicional em quilates
fig = sns.displot(
data=diamonds,
x="carat", hue="cut",
kind="kde", height=6,
multiple="fill", clip=(0, None),
palette="ch:rot=-.25,hue=1,light=.75",
)
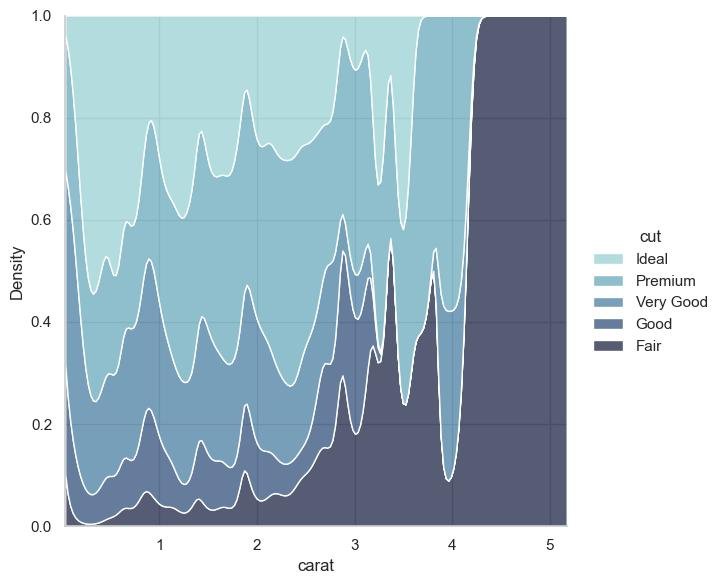
2.1.4.24 - Parcelas ECDF facetadas
import seaborn as sns
sns.set_theme(style="ticks")
df = sns.load_dataset("mpg")
colors = (250, 70, 50), (350, 70, 50)
cmap = sns.blend_palette(colors, input="husl", as_cmap=True)
fig = sns.displot(
df,
x="displacement", col="origin", hue="model_year",
kind="ecdf", aspect=.75, linewidth=2, palette=cmap,
)
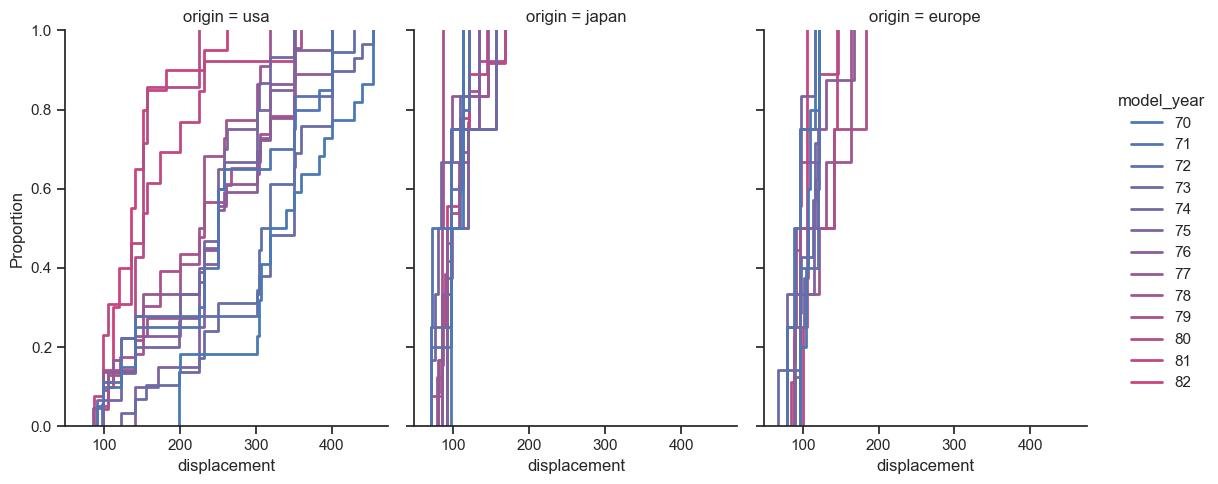
2.1.4.25 - Regressão linear múltipla
import seaborn as sns
sns.set_theme()
# Carregar o conjunto de dados dos pinguins
penguins = sns.load_dataset("penguins")
# Trace a largura da sépala como uma função do comprimento_da_sépala ao longo dos dias
fig = sns.lmplot(
data=penguins, x="bill_length_mm", y="bill_depth_mm",
hue="species", height=5
)
# Use more informative axis labels than are provided by default
fig.set_axis_labels("Snoot length (mm)", "Snoot depth (mm)")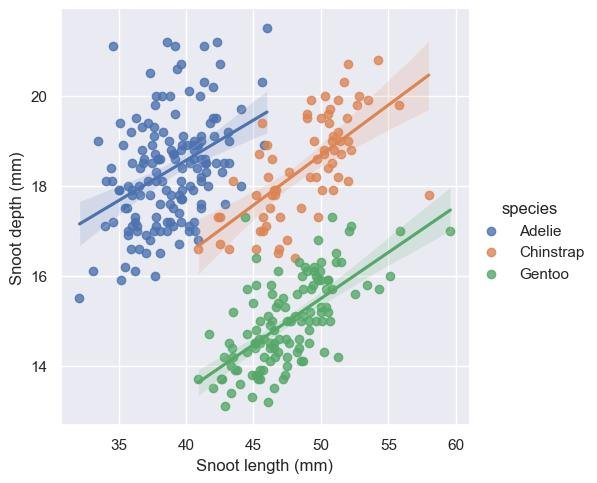
2.1.4.26 - Densidade pareada e matriz do gráfico de dispersão
import seaborn as sns
sns.set_theme(style="white")
df = sns.load_dataset("penguins")
fig = sns.PairGrid(df, diag_sharey=False)
fig.map_upper(sns.scatterplot, s=15)
fig.map_lower(sns.kdeplot)
fig.map_diag(sns.kdeplot, lw=2)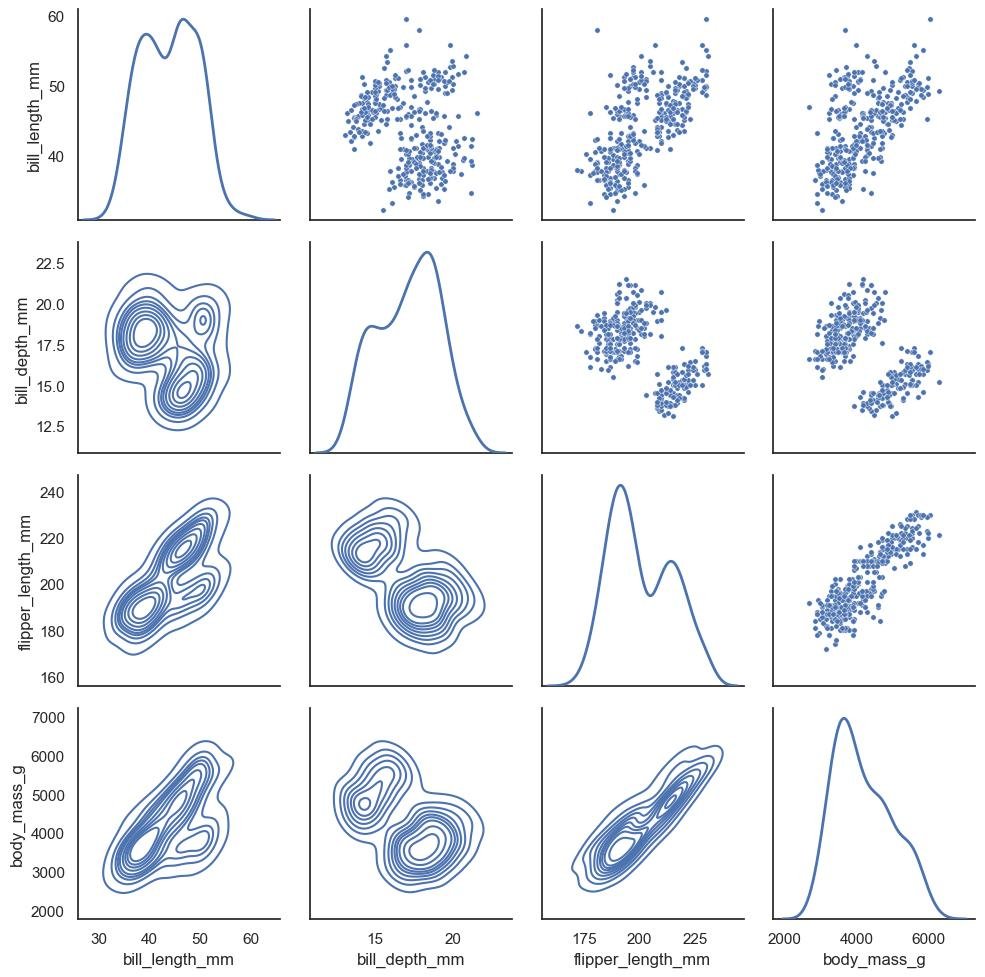
2.1.4.27 - Gráficos categóricos pareados
import seaborn as sns
sns.set_theme(style="whitegrid")
# Carregue o exemplo de conjunto de dados do Titanic
titanic = sns.load_dataset("titanic")
# Configure uma grade para plotar a probabilidade de sobrevivência contra várias variáveis
fig = sns.PairGrid(
titanic, y_vars="survived",
x_vars=["pclass", "sex", "who", "alone"],
height=5, aspect=.5)
# Desenhe um gráfico de pontos marítimos em cada eixo
fig.map(sns.pointplot, scale=1.3, errwidth=4, color="xkcd:plum")
fig.set(ylim=(0, 1))
sns.despine(fig=fig.fig, left=True)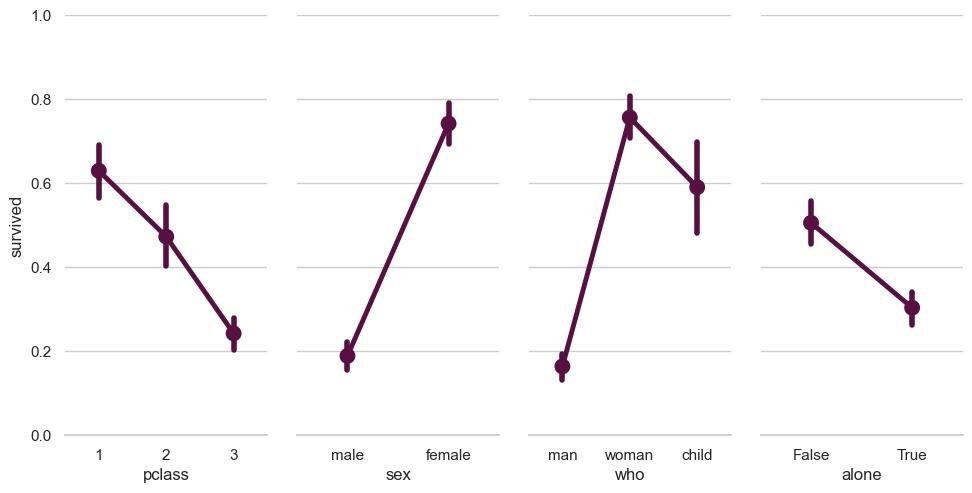
2.1.4.28 - Gráfico de pontos com várias variáveis
import seaborn as sns
sns.set_theme(style="whitegrid")
# Carregar o conjunto de dados
crashes = sns.load_dataset("car_crashes")
# Faça o PairGrid
fig = sns.PairGrid(crashes.sort_values("total", ascending=False),
x_vars=crashes.columns[:-3], y_vars=["abbrev"],
height=10, aspect=.25)
# Desenhe um gráfico de pontos usando a função stripplot
fig.map(sns.stripplot, size=10, orient="h", jitter=False,
palette="flare_r", linewidth=1, edgecolor="w")
# Use os mesmos limites do eixo x em todas as colunas e adicione rótulos melhores
fig.set(xlim=(0, 25), xlabel="Crashes", ylabel="")
# Use títulos semanticamente significativos para as colunas
titles = [
"Acidentes totais", "Acidentes por excesso de velocidade", "Acidentes com álcool",
"Sem falhas distraídas", "Sem falhas anteriores"
]
for ax, title in zip(fig.axes.flat, titles):
# Defina um título diferente para cada eixo
ax.set(title=title)
# Faça a grade horizontal em vez de vertical
ax.xaxis.grid(False)
ax.yaxis.grid(True)
sns.despine(left=True, bottom=True)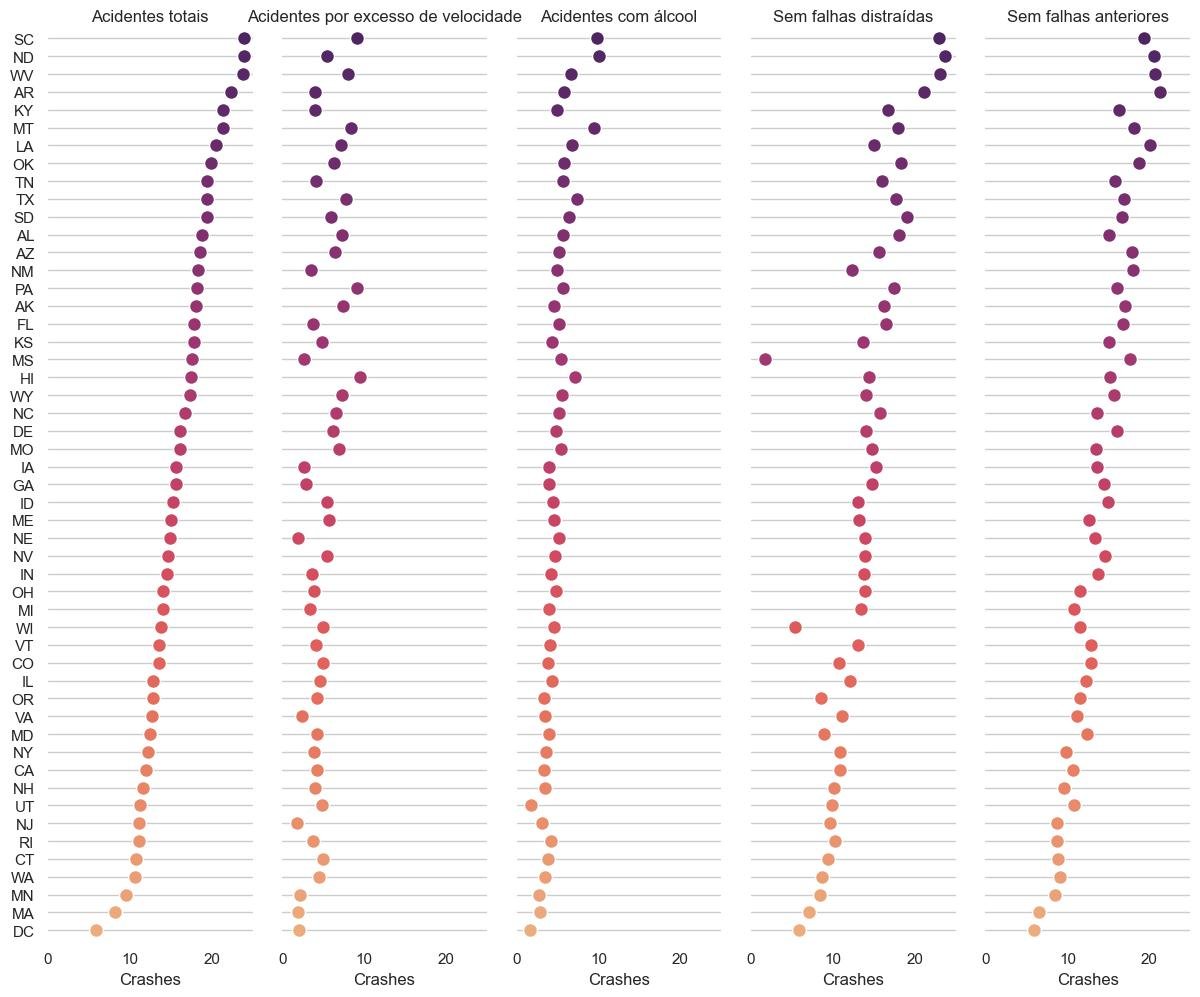
2.1.4.29 - Opções de paleta de cores
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
sns.set_theme(style="white", context="talk")
rs = np.random.RandomState(8)
# Configurar a figura matplotlib
fig, (ax1, ax2, ax3) = plt.subplots(3, 1, figsize=(7, 5), sharex=True)
# Gerar alguns dados sequenciais
x = np.array(list("ABCDEFGHIJ"))
y1 = np.arange(1, 11)
sns.barplot(x=x, y=y1, palette="rocket", ax=ax1)
ax1.axhline(0, color="k", clip_on=False)
ax1.set_ylabel("Sequential")
# Centralize os dados para torná-los divergentes
y2 = y1 - 5.5
sns.barplot(x=x, y=y2, palette="vlag", ax=ax2)
ax2.axhline(0, color="k", clip_on=False)
ax2.set_ylabel("Diverging")
# Reordene aleatoriamente os dados para torná-los qualitativos
y3 = rs.choice(y1, len(y1), replace=False)
sns.barplot(x=x, y=y3, palette="deep", ax=ax3)
ax3.axhline(0, color="k", clip_on=False)
ax3.set_ylabel("Qualitative")
# Finalize o enredo
sns.despine(bottom=True)
plt.setp(fig.axes, yticks=[])
plt.tight_layout(h_pad=2)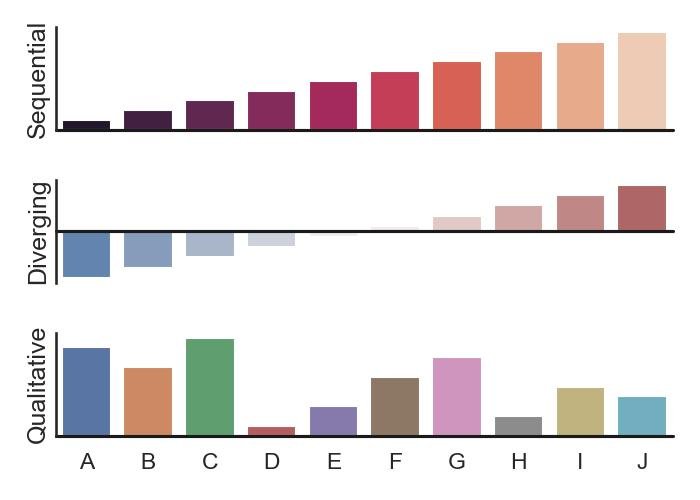
2.2 - Medidas de tendência central e dispersão robustas
2.3 - Análise de correlação e covariância multivariada
2.4 - Análise de componentes principais e análise fatorial
Arduino
Coautor
Betobyte
Autor
Autores
