9 - Métodos Bayesianos

A inferência bayesiana é uma abordagem estatística que se baseia no Teorema de Bayes para fazer inferências sobre parâmetros desconhecidos de uma distribuição de probabilidade.

Os fundamentos da inferência bayesiana incluem os seguintes conceitos:

• Priori: A priori é a distribuição de probabilidade que representa o conhecimento prévio ou as crenças sobre os parâmetros antes de observar os dados. Ela expressa a incerteza inicial sobre os parâmetros e pode ser baseada em informações históricas, estudos anteriores ou conhecimento especializado.
• Verossimilhança: A verossimilhança é a função de densidade de probabilidade dos dados, condicional nos parâmetros. Ela descreve a probabilidade de observar os dados dada uma configuração específica dos parâmetros.
• Posteriori: A posteriori é a distribuição de probabilidade atualizada dos parâmetros, levando em consideração os dados observados. É calculada aplicando o Teorema de Bayes, que combina a priori e a verossimilhança para obter a distribuição posteriori.
• Função de verossimilhança marginal: A função de verossimilhança marginal é obtida integrando-se a verossimilhança em relação aos parâmetros, ponderada pela distribuição priori. Ela fornece uma medida da evidência dos dados para diferentes valores dos parâmetros, levando em consideração a incerteza antes da observação dos dados.
• Estimativa pontual: A estimativa pontual na inferência bayesiana é representada pela média, mediana ou modo da distribuição posteriori. Essa estimativa representa o valor mais provável ou o valor central dos parâmetros desconhecidos, levando em consideração tanto a priori quanto a informação dos dados.
• Intervalo de credibilidade: O intervalo de credibilidade é uma faixa de valores que contém uma proporção especificada da distribuição posteriori. É usado para quantificar a incerteza sobre os parâmetros desconhecidos e é análogo ao intervalo de confiança na inferência clássica.

Esses são alguns dos fundamentos da inferência bayesiana.

Essa abordagem oferece uma maneira flexível e intuitiva de lidar com incertezas e atualizar as crenças à medida que novos dados são observados.

Ela tem aplicações em uma variedade de áreas, incluindo ciências, medicina, finanças e aprendizado de máquina.

9.1.1.1 - Priori

Na inferência bayesiana, a priori é uma distribuição de probabilidade que expressa o conhecimento prévio ou as crenças sobre os parâmetros antes de observar os dados. Ela reflete a incerteza inicial sobre os parâmetros e fornece uma base para atualizar essa incerteza à medida que os dados são analisados.

A escolha da priori é um aspecto crucial na inferência bayesiana, pois influencia diretamente a distribuição posteriori dos parâmetros. Existem diferentes tipos de priors que podem ser utilizados, dependendo do conhecimento disponível e das suposições feitas sobre os parâmetros. Aqui estão alguns tipos comuns de priors:

Priori não informativa: Uma priori não informativa é usada quando não há conhecimento prévio ou quando se deseja que os dados dominem completamente a inferência. Ela é geralmente escolhida como uma distribuição plana ou uniforme, onde todos os valores possíveis são igualmente prováveis. Essa escolha de priori não influencia fortemente a posteriori e permite que os dados forneçam a maior parte da informação.

Priori informativa: Uma priori informativa é usada quando há algum conhecimento prévio sobre os parâmetros. Ela pode ser baseada em estudos anteriores, especialistas no assunto ou informações históricas. Essa priori incorpora as informações disponíveis e tem maior influência sobre a posteriori. Priors informativas podem ser escolhidas com base em distribuições específicas, como distribuições normais, exponenciais, gamma, entre outras.

Priori conjugada: Uma priori conjugada é uma priori que, combinada com uma verossimilhança específica, produz uma posteriori com a mesma forma funcional da priori. Isso simplifica os cálculos, pois a posteriori pode ser determinada analiticamente. As priors conjugadas são escolhidas para que a atualização bayesiana seja feita de maneira mais direta.

É importante destacar que a escolha da priori pode ser subjetiva e pode influenciar os resultados da inferência bayesiana. Diferentes priors podem levar a diferentes conclusões, e a escolha da priori deve ser fundamentada em conhecimento prévio confiável ou em uma abordagem mais neutra, dependendo do contexto do problema.

A principal vantagem da inferência bayesiana é que a priori e a verossimilhança são combinadas para produzir uma posteriori que reflete a incerteza atualizada após a observação dos dados. Essa abordagem permite incorporar informações prévias e atualizá-las à medida que mais dados são analisados, resultando em inferências mais precisas e robustas.

Na inferência bayesiana, a especificação da priori envolve a escolha de uma distribuição de probabilidade que representa o conhecimento prévio ou as crenças sobre os parâmetros de interesse.

No Python, a biblioteca scipy.stats fornece várias distribuições de probabilidade predefinidas que podem ser utilizadas como priors.

Aqui está um exemplo de código Python para especificar uma priori normal:

import scipy.stats as stats

# Especificação da priori normal com média 0 e desvio padrão 1
priori = stats.norm(loc=0, scale=1)

Nesse exemplo, a função stats.norm é usada para criar uma distribuição normal com média (loc) igual a 0 e desvio padrão (scale) igual a 1.

Esses parâmetros podem ser ajustados de acordo com o conhecimento prévio ou as suposições feitas sobre os parâmetros.

Após especificar a priori, ela pode ser combinada com a verossimilhança dos dados para obter a posteriori usando métodos de inferência bayesiana, como a amostragem de Monte Carlo Markov Chain (MCMC).

O pacote pymc3 é uma biblioteca popular para realizar inferência bayesiana no Python e fornece uma interface conveniente para especificar a priori, a verossimilhança e realizar a inferência.

É importante destacar que a escolha da priori depende do contexto do problema, do conhecimento prévio disponível e das suposições feitas. Ela pode ser tanto informativa, quando há conhecimento prévio substancial, quanto não informativa, quando não há informações adicionais disponíveis. A escolha da priori pode afetar os resultados da inferência bayesiana, portanto, é importante considerar cuidadosamente essa etapa do processo.

9.1.1.2 - Verossimilhança

A verossimilhança é uma função que descreve a probabilidade de observar os dados observados, dada uma hipótese sobre os parâmetros do modelo. Na inferência bayesiana, a verossimilhança é usada em conjunto com a priori para obter a posteriori, que é a distribuição de probabilidade dos parâmetros dado os dados.

A forma da função de verossimilhança depende do modelo estatístico que está sendo utilizado. Em muitos casos, assume-se que os dados são independentes e identicamente distribuídos (iid), o que simplifica a verossimilhança. Por exemplo, se estamos modelando os dados como uma distribuição normal, a verossimilhança será a função de densidade de probabilidade da distribuição normal.

No Python, é possível utilizar bibliotecas como scipy.stats para obter funções de verossimilhança pré-definidas. Essas funções permitem calcular a verossimilhança dos dados observados dado um conjunto de parâmetros do modelo. Aqui está um exemplo de código Python que ilustra como calcular a verossimilhança para dados seguindo uma distribuição normal:

import scipy.stats as stats

# Dados observados
dados = [1.5, 2.0, 2.5, 3.0]

# Parâmetros do modelo
media = 2.0
desvio_padrao = 0.5

# Cálculo da verossimilhança
verossimilhanca = stats.norm(loc=media, scale=desvio_padrao).pdf(dados).prod()

Nesse exemplo, a função stats.norm é utilizada para criar uma distribuição normal com média media e desvio padrão desvio_padrao.

A função pdf é então aplicada aos dados observados para obter a função de densidade de probabilidade correspondente.

Em seguida, o produto das densidades de probabilidade é calculado para obter a verossimilhança.

A verossimilhança é uma peça fundamental na inferência bayesiana, pois fornece uma medida de quão provável é observar os dados dados os parâmetros do modelo.

Ela é combinada com a priori por meio do Teorema de Bayes para obter a posteriori, que é a distribuição de probabilidade dos parâmetros atualizada com base nos dados observados.

9.1.1.3 - Posteriori

A posteriori é a distribuição de probabilidade dos parâmetros de um modelo estatístico, atualizada com base nos dados observados e nas informações prévias disponíveis na forma da priori. Ela representa a distribuição de probabilidade dos parâmetros condicionada aos dados observados.

A obtenção da posteriori é feita por meio do Teorema de Bayes, que estabelece a relação entre a priori, a verossimilhança e a evidência (ou verossimilhança marginal). Matematicamente, o Teorema de Bayes pode ser expresso da seguinte forma:

P(θ | D) = P(D | θ) * P(θ) / P(D)

onde:

P(θ | D) é a posteriori, que representa a distribuição de probabilidade dos parâmetros θ dado os dados D.

P(D | θ) é a verossimilhança, que representa a probabilidade dos dados D dado um conjunto específico de parâmetros θ.

P(θ) é a priori, que representa a distribuição de probabilidade dos parâmetros θ antes de observar os dados.

P(D) é a evidência ou verossimilhança marginal, que é a probabilidade dos dados D considerando todas as possíveis combinações de parâmetros.

A posteriori é importante na inferência bayesiana, pois fornece uma distribuição de probabilidade completa dos parâmetros, levando em consideração tanto a informação dos dados observados quanto as informações prévias expressas pela priori.

Ela permite a estimativa dos parâmetros, a realização de previsões e a tomada de decisões baseada nas probabilidades condicionais.

No Python, a posteriori pode ser obtida usando bibliotecas como pymc3, Stan ou PyStan, que oferecem ferramentas para realizar inferência bayesiana e calcular a posteriori de forma eficiente.

Essas bibliotecas permitem especificar modelos estatísticos, definir as prioris, calcular a verossimilhança e obter a posteriori usando algoritmos de amostragem, como a Cadeia de Markov Monte Carlo (MCMC).

A obtenção da posteriori em um problema específico requer a definição do modelo estatístico, a especificação da priori e a implementação de um algoritmo para realizar a inferência bayesiana.

Dessa forma, não há um código Python único para calcular a posteriori em todos os casos.

No entanto, vou fornecer um exemplo básico de como calcular a posteriori em um cenário simples.

Suponha que estamos interessados em estimar a média de uma distribuição normal com uma priori também normal.

Vamos supor que temos uma amostra de dados observados e queremos calcular a posteriori para a média.

import numpy as np
import scipy.stats as stats

# Dados observados
dados = np.array([1.2, 2.5, 0.8, 1.9, 1.5])

# Definir priori
media_priori = 0  # média da priori
desvio_priori = 1  # desvio padrão da priori

# Parâmetros da distribuição posteriori
media_posteriori = (desvio_priori**2 * np.mean(dados) + len(dados) * media_priori) / (desvio_priori**2 + len(dados))
desvio_posteriori = np.sqrt(1 / (1/desvio_priori**2 + len(dados)))

# Calcular a posteriori para um determinado valor observado
valor_observado = 1.7
posteriori = stats.norm.pdf(valor_observado, loc=media_posteriori, scale=desvio_posteriori)

print("Posteriori:", posteriori)

Neste exemplo, usamos a biblioteca scipy.stats para calcular a função de densidade de probabilidade (pdf) da distribuição normal.

A posteriori é calculada com base na fórmula para atualização da média e do desvio padrão quando se tem uma priori normal e dados observados.

Este é apenas um exemplo simples e a forma de calcular a posteriori dependerá do modelo estatístico e das especificações da priori em cada problema.

9.1.1.4 - Função de verossimilhança marginal

A função de verossimilhança marginal, também conhecida como função de evidência ou fator de normalização, descreve a probabilidade conjunta dos dados observados dado um modelo estatístico e um conjunto de parâmetros. Ela é uma quantidade importante na inferência bayesiana, pois é usada para calcular a posteriori através do teorema de Bayes.

A verossimilhança marginal é obtida integrando-se a função de verossimilhança conjunta sobre todos os possíveis valores dos parâmetros. Ela representa a probabilidade de observar os dados observados em todo o espaço de parâmetros considerado.

A fórmula geral para a função de verossimilhança marginal é dada por:

L(D) = ∫ L(D | θ) * p(θ) dθ

onde L(D) é a função de verossimilhança marginal, L(D | θ) é a função de verossimilhança condicional, p(θ) é a priori dos parâmetros θ e dθ representa a integral em relação aos parâmetros.

A função de verossimilhança marginal é útil para comparar diferentes modelos estatísticos ou diferentes conjuntos de parâmetros dentro de um mesmo modelo. Ela fornece uma medida de ajuste dos dados aos modelos considerados, permitindo a seleção do modelo mais apropriado.

No contexto da inferência bayesiana, a função de verossimilhança marginal é utilizada para normalizar a posteriori, garantindo que a distribuição posteriori seja uma densidade de probabilidade válida.

Em resumo, a função de verossimilhança marginal é uma medida da adequação dos dados observados a um modelo estatístico específico, levando em consideração todas as possíveis combinações de valores dos parâmetros do modelo.

A função de verossimilhança marginal não pode ser calculada diretamente a partir de um código Python, pois requer a definição específica da função de verossimilhança condicional e da priori dos parâmetros.

No entanto, podemos formular um exemplo simplificado para ilustrar como calcular a verossimilhança marginal em um caso específico.

Suponha que tenhamos uma função de verossimilhança condicional L(D | θ) e uma priori p(θ) definidas.

Para calcular a verossimilhança marginal, precisamos integrar o produto da função de verossimilhança condicional e da priori sobre todos os possíveis valores dos parâmetros.

Aqui está um exemplo genérico de como você poderia calcular a verossimilhança marginal usando a biblioteca NumPy:

import numpy as np

# Definir a função de verossimilhança condicional L(D | θ)
def likelihood(data, params):
    # Implemente sua função de verossimilhança condicional aqui
    # Ela deve retornar a verossimilhança condicional para os dados fornecidos e os parâmetros θ
    pass

# Definir a priori p(θ)
def prior(params):
    # Implemente sua priori aqui
    # Ela deve retornar a priori para os parâmetros θ
    pass

# Definir os dados observados
data = [...]

# Definir uma grade de valores para os parâmetros θ
theta_values = [...]

# Inicializar a verossimilhança marginal
marginal_likelihood = 0

# Calcular a verossimilhança marginal
for theta in theta_values:
    likelihood_conditional = likelihood(data, theta)
    prior_value = prior(theta)
    marginal_likelihood += likelihood_conditional * prior_value

# Imprimir o resultado
print("Verossimilhança marginal:", marginal_likelihood)

Lembre-se de que este é apenas um exemplo genérico e que você precisará adaptá-lo de acordo com sua função de verossimilhança condicional e priori específicas.

9.1.1.5 - Estimativa pontual

A estimativa pontual é um conceito importante na inferência bayesiana e refere-se à obtenção de um único valor para um parâmetro desconhecido com base nos dados observados. Diferentemente da inferência clássica, que geralmente envolve estimativas como a média amostral ou a máxima verossimilhança, a inferência bayesiana fornece estimativas pontuais baseadas na distribuição a posteriori do parâmetro.

A estimativa pontual mais comumente usada na inferência bayesiana é a média a posteriori, também chamada de estimativa da média posterior ou estimativa bayesiana. Essa estimativa é calculada como o valor esperado da distribuição a posteriori do parâmetro.

Suponha que θ seja o parâmetro desconhecido e que tenhamos uma distribuição a posteriori p(θ | D) para o parâmetro com base nos dados observados D. A estimativa da média posterior é dada por:

θ̂ = E[θ | D] = ∫ θ p(θ | D) dθ

onde E[θ | D] representa o valor esperado do parâmetro θ dado os dados D.

Para calcular a estimativa pontual utilizando a média a posteriori em Python, você precisa ter acesso à distribuição a posteriori do parâmetro. Você pode obter essa distribuição a partir de uma amostra de cadeia de Markov Monte Carlo (MCMC) ou através de outras técnicas de inferência bayesiana.

Aqui está um exemplo simples de como calcular a estimativa pontual usando a média a posteriori com a biblioteca PyMC3:

import pymc3 as pm

# Definir o modelo bayesiano usando a biblioteca PyMC3
with pm.Model() as model:
    # Definir as prioris para o parâmetro θ
    theta = pm.Normal('theta', mu=0, sd=1)

    # Definir a verossimilhança dos dados observados
    likelihood = ...

    # Definir a distribuição a posteriori
    posterior = pm.sample_posterior_predictive([theta])

# Calcular a estimativa da média posterior
mean_posterior = posterior['theta'].mean()

# Imprimir o resultado
print("Estimativa da média posterior:", mean_posterior)

Neste exemplo, você precisa definir o modelo bayesiano completo usando a biblioteca PyMC3, incluindo as prioris para o parâmetro θ e a verossimilhança dos dados observados. Em seguida, você pode usar a função sample_posterior_predictive para amostrar a distribuição a posteriori do parâmetro e, finalmente, calcular a média a posteriori utilizando o método .mean().

Lembre-se de que este é apenas um exemplo básico e que a implementação exata dependerá do seu problema específico e das bibliotecas ou técnicas de inferência bayesiana que você estiver usando.

9.1.1.6 - Intervalo de credibilidade

O intervalo de credibilidade é um conceito importante na inferência bayesiana e fornece uma faixa de valores plausíveis para um parâmetro desconhecido com base na distribuição a posteriori. Diferentemente dos intervalos de confiança da inferência clássica, que se referem à variabilidade dos estimadores, os intervalos de credibilidade têm uma interpretação mais direta como uma medida de incerteza sobre o parâmetro.

Um intervalo de credibilidade é construído de tal forma que contém uma porcentagem especificada de probabilidade da distribuição a posteriori. Por exemplo, um intervalo de credibilidade de 95% indica que há uma probabilidade de 95% de que o verdadeiro valor do parâmetro esteja contido nesse intervalo.

Existem diferentes métodos para calcular intervalos de credibilidade, dependendo da forma da distribuição a posteriori e das suposições feitas. Alguns métodos comuns incluem:

Intervalo de credibilidade mais provável: também conhecido como intervalo de credibilidade de massa máxima, é um intervalo que contém os valores mais prováveis do parâmetro. É calculado encontrando os limites superior e inferior que correspondem aos quantis acumulados de probabilidade desejados da distribuição a posteriori.

Intervalo de credibilidade simétrico: é um intervalo simétrico em torno do valor esperado do parâmetro, que contém uma porcentagem especificada de probabilidade. É calculado determinando os quantis acumulados de probabilidade adequados da distribuição a posteriori.

Intervalo de credibilidade assimétrico: é um intervalo que não é simétrico em torno do valor esperado do parâmetro, levando em consideração a assimetria da distribuição a posteriori. Este intervalo fornece uma representação mais precisa da incerteza do parâmetro quando a distribuição a posteriori é assimétrica.

A implementação de intervalos de credibilidade em Python depende da biblioteca ou técnica específica que você está usando para a inferência bayesiana. Muitas bibliotecas populares, como PyMC3 e Stan, fornecem métodos para calcular intervalos de credibilidade a partir da distribuição a posteriori estimada.

Aqui está um exemplo básico de como calcular um intervalo de credibilidade mais provável em Python usando a biblioteca PyMC3:

import pymc3 as pm

# Definir o modelo bayesiano usando a biblioteca PyMC3
with pm.Model() as model:
    # Definir as prioris para o parâmetro θ
    theta = pm.Normal('theta', mu=0, sd=1)

    # Definir a verossimilhança dos dados observados
    likelihood = ...

    # Definir a distribuição a posteriori
    posterior = pm.sample_posterior_predictive([theta])

# Calcular o intervalo de credibilidade mais provável de 95%
credible_interval = pm.stats.hpd(posterior['theta'], hdi_prob=0.95)

# Imprimir o resultado
print("Intervalo de credibilidade mais provável de 95%:", credible_interval)

Neste exemplo, você define o modelo bayesiano completo usando a biblioteca PyMC3 e estima a distribuição a posteriori do parâmetro θ.

Em seguida, você usa a função pm.stats.hpd para calcular o intervalo de credibilidade mais provável com uma probabilidade de 95%.

Lembre-se de que este é apenas um exemplo básico e que a implementação exata do intervalo de credibilidade dependerá do seu problema específico e das bibliotecas ou técnicas de inferência bayesiana que você estiver usando.

A modelagem bayesiana de regressão oferece uma abordagem flexível e poderosa para análise de dados. A seguir, detalho alguns tipos comuns de modelos de regressão bayesiana:

• Regressão Linear Bayesiana: a regressão linear bayesiana estende o modelo clássico de regressão linear incorporando a incerteza nos coeficientes do modelo. Os coeficientes são tratados como variáveis aleatórias, e são atribuídas distribuições a priori para eles. Com base nos dados observados e nas distribuições a priori, é calculada a distribuição a posteriori dos coeficientes, fornecendo estimativas probabilísticas para os mesmos.
• Regressão Logística Bayesiana: a regressão logística bayesiana é usada quando o resultado esperado é uma variável binária. Ela estende o modelo clássico de regressão logística ao tratar os coeficientes como variáveis aleatórias e atribuir distribuições a priori para eles. A distribuição a posteriori dos coeficientes é calculada com base nos dados observados e nas distribuições a priori, permitindo a obtenção de estimativas probabilísticas.
• Regressão Bayesiana com Variáveis de Resposta Multinomial: a regressão bayesiana com variáveis de resposta multinomial é aplicada quando o resultado esperado é uma variável categórica com mais de duas categorias. Ela estende o modelo clássico de regressão multinomial ao tratar os coeficientes como variáveis aleatórias e atribuir distribuições a priori para eles. A distribuição a posteriori dos coeficientes é calculada com base nos dados observados e nas distribuições a priori, permitindo a obtenção de estimativas probabilísticas.
• Regressão Bayesiana Não Linear: a regressão bayesiana não linear é usada quando o relacionamento entre as variáveis independentes e a variável dependente não pode ser modelado adequadamente por uma relação linear. Nesse caso, modelos não lineares, como polinomiais, exponenciais, logísticos, entre outros, são especificados. Os coeficientes desses modelos não lineares são tratados como variáveis aleatórias, e distribuições a priori são atribuídas a eles. A distribuição a posteriori dos coeficientes é calculada com base nos dados observados e nas distribuições a priori.

Esses são apenas alguns exemplos de modelagem bayesiana de regressão.

A modelagem bayesiana permite uma maior flexibilidade na especificação do modelo, incorporando incerteza nos coeficientes e fornecendo estimativas probabilísticas.

No entanto, a escolha adequada da priori e a computação da posteriori podem ser desafiadoras em modelos mais complexos.

9.2.1.1 - Regressão Linear Bayesiana

A regressão linear bayesiana é uma abordagem da regressão linear que incorpora princípios da inferência bayesiana. Ela permite estimar os parâmetros do modelo e fazer previsões usando uma distribuição a posteriori completa em vez de apenas estimativas pontuais.

Na regressão linear bayesiana, os parâmetros do modelo são tratados como variáveis aleatórias com distribuições a priori especificadas. Essas distribuições a priori representam o conhecimento ou crenças iniciais sobre os parâmetros antes de observar os dados. Em seguida, a distribuição a posteriori dos parâmetros é atualizada com base nos dados observados usando o teorema de Bayes.

Para realizar a regressão linear bayesiana, é necessário especificar tanto a distribuição a priori quanto a verossimilhança dos dados. A distribuição a priori pode ser escolhida de acordo com o conhecimento prévio ou suposições sobre os parâmetros. A verossimilhança representa o relacionamento entre os dados observados e os parâmetros do modelo.

Uma vez que a distribuição a posteriori dos parâmetros é obtida, é possível estimar os parâmetros por meio de medidas resumo, como a média a posteriori, a moda a posteriori ou a mediana a posteriori. Além disso, é possível fazer previsões usando a distribuição a posteriori dos parâmetros, obtendo uma distribuição preditiva dos valores alvo para novos dados.

A principal vantagem da regressão linear bayesiana é que ela fornece uma estimativa completa da incerteza dos parâmetros e das previsões. Em vez de ter apenas um único valor estimado, é possível obter uma distribuição completa, que reflete a variabilidade e incerteza associadas aos parâmetros e às previsões.

A implementação da regressão linear bayesiana em Python pode ser feita usando bibliotecas como PyMC3, Stan ou TensorFlow Probability, que fornecem ferramentas para modelagem bayesiana. Essas bibliotecas permitem especificar o modelo, estimar a distribuição a posteriori dos parâmetros e realizar previsões. O código pode variar dependendo da biblioteca escolhida, mas em geral envolve a definição do modelo, a especificação das distribuições a priori e da verossimilhança, a amostragem da distribuição a posteriori e a análise dos resultados.

Aqui está um exemplo básico de regressão linear bayesiana usando a biblioteca PyMC3:

import pymc3 as pm
import numpy as np

# Dados de entrada
X = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 6, 8, 10])

# Definir o modelo bayesiano usando a biblioteca PyMC3
with pm.Model() as model:
    # Definir as prioris para os parâmetros
    alpha = pm.Normal('alpha', mu=0, sd=10)
    beta = pm.Normal('beta', mu=0, sd=10)

    # Definir a verossimilhança dos dados observados
    likelihood = pm.Normal('y', mu=alpha + beta*X, sd=1, observed=y)

    # Amostrar a distribuição a posteriori dos parâmetros
    trace = pm.sample(1000)

# Análise dos resultados
sumario = pm.summary(trace)
print(sumario)

Neste exemplo, estamos realizando uma regressão linear simples em que estamos tentando prever y a partir de X. Definimos distribuições normais como prioris para os parâmetros alpha e beta. Em seguida, especificamos uma verossimilhança normal para os dados observados y, assumindo um desvio padrão de 1. Através da amostragem da distribuição a posteriori usando a função sample do PyMC3, obtemos uma cadeia de amostras que representa a distribuição a posteriori dos parâmetros. Por fim, podemos analisar os resultados usando a função summary do PyMC3 para obter estimativas dos parâmetros e suas incertezas.

É importante notar que a regressão linear bayesiana pode ser estendida para casos mais complexos, como regressão linear múltipla, regressão logística, modelos hierárquicos, entre outros. A escolha das prioris e a especificação do modelo dependerão da natureza do problema e das suposições feitas. Além disso, a escolha adequada de hiperparâmetros, o tamanho da cadeia de amostras e a convergência da amostragem são aspectos cruciais para obter resultados confiáveis.

9.2.1.2 - Regressão Logística Bayesiana

A regressão logística bayesiana é uma abordagem da regressão logística que utiliza princípios da inferência bayesiana para estimar os parâmetros do modelo e fazer previsões. Ao contrário da regressão logística clássica, que fornece apenas estimativas pontuais dos parâmetros, a regressão logística bayesiana permite obter distribuições a posteriori completas dos parâmetros, o que oferece uma visão mais completa da incerteza associada a esses parâmetros.

Na regressão logística bayesiana, os parâmetros do modelo são tratados como variáveis aleatórias com distribuições a priori especificadas. Essas distribuições a priori refletem o conhecimento ou as crenças iniciais sobre os parâmetros antes de observar os dados. Em seguida, a distribuição a posteriori dos parâmetros é atualizada com base nos dados observados usando o teorema de Bayes.

Para realizar a regressão logística bayesiana, é necessário especificar tanto as distribuições a priori quanto a verossimilhança dos dados. A distribuição a priori pode ser escolhida com base no conhecimento prévio ou nas suposições sobre os parâmetros. A verossimilhança representa o relacionamento entre os dados observados e os parâmetros do modelo, seguindo a distribuição binomial.

Uma vez que a distribuição a posteriori dos parâmetros é obtida, é possível fazer estimativas pontuais usando medidas resumo, como a média a posteriori, a moda a posteriori ou a mediana a posteriori. Além disso, a distribuição a posteriori permite calcular intervalos de credibilidade, que fornecem uma medida da incerteza dos parâmetros. Também é possível fazer previsões usando a distribuição a posteriori dos parâmetros, obtendo uma distribuição preditiva das classes para novos dados.

A principal vantagem da regressão logística bayesiana é a capacidade de modelar a incerteza associada aos parâmetros e às previsões. Isso é particularmente útil em situações com conjuntos de dados pequenos ou ruidosos, em que a incerteza é mais pronunciada. Além disso, a inferência bayesiana permite incorporar informações a priori, regularizando os parâmetros do modelo e evitando problemas de sobreajuste.

A implementação da regressão logística bayesiana em Python pode ser feita usando bibliotecas como PyMC3, Stan ou TensorFlow Probability, que fornecem ferramentas para modelagem bayesiana. Essas bibliotecas permitem especificar o modelo, estimar a distribuição a posteriori dos parâmetros e realizar previsões. O código pode variar dependendo da biblioteca escolhida, mas geralmente envolve a definição do modelo, a especificação das distribuições a priori e da verossimilhança, a amostragem da distribuição a posteriori e a análise dos resultados.

Aqui está um exemplo básico de regressão logística bayesiana usando a biblioteca PyMC3:

import pymc3 as pm
import numpy as np

# Dados de entrada
X = np.array([[1, 2], [2, 3], [3, 4], [4, 5]])
y = np.array([0, 0, 1, 1])

# Definir o modelo
with pm.Model() as model:
    # Priori para os coeficientes
    beta = pm.Normal('beta', mu=0, sd=1, shape=X.shape[1])
    # Verossimilhança binomial
    p = pm.math.sigmoid(pm.math.dot(X, beta))
    likelihood = pm.Bernoulli('likelihood', p=p, observed=y)

    # Amostragem da distribuição a posteriori
    trace = pm.sample(1000, tune=1000)

# Análise dos resultados
sumario = pm.summary(trace)
print(sumario)

Neste exemplo, estamos realizando uma regressão logística bayesiana simples em que estamos tentando prever a classe y a partir das variáveis X.

Definimos distribuições normais como prioris para os coeficientes beta. Especificamos a verossimilhança binomial para os dados observados y.

Através da amostragem da distribuição a posteriori usando a função sample do PyMC3, obtemos uma cadeia de amostras que representa a distribuição a posteriori dos coeficientes.

Por fim, podemos analisar os resultados usando a função summary do PyMC3 para obter estimativas dos coeficientes e suas incertezas.

É importante notar que a regressão logística bayesiana pode ser estendida para casos mais complexos, como regressão logística multinomial, modelos hierárquicos, entre outros.

A escolha das prioris e a especificação do modelo dependerão da natureza do problema e das suposições feitas.

Além disso, a escolha adequada de hiperparâmetros, o tamanho da cadeia de amostras e a convergência da amostragem são aspectos cruciais para obter resultados confiáveis.

9.2.1.3 - Regressão Bayesiana com Variáveis de Resposta Multinomial

A regressão bayesiana com variáveis de resposta multinomial é uma extensão da regressão bayesiana para casos em que a variável dependente possui mais de duas categorias. É uma abordagem flexível que permite modelar relações entre variáveis independentes e uma variável dependente com várias categorias.

Na regressão bayesiana com variáveis de resposta multinomial, o objetivo é estimar a distribuição a posteriori dos parâmetros do modelo, que capturam as relações entre as variáveis independentes e as categorias da variável dependente. Esses parâmetros são tratados como variáveis aleatórias com distribuições a priori especificadas. A distribuição a priori reflete o conhecimento ou as crenças iniciais sobre os parâmetros antes de observar os dados.

Para realizar a regressão bayesiana com variáveis de resposta multinomial, é necessário especificar as distribuições a priori para os parâmetros do modelo e a verossimilhança dos dados. A distribuição a priori pode ser escolhida com base no conhecimento prévio ou nas suposições sobre os parâmetros. A verossimilhança representa o relacionamento entre as variáveis independentes e a variável dependente multinomial, seguindo uma distribuição multinomial.

Uma vez que a distribuição a posteriori dos parâmetros é obtida, é possível fazer estimativas pontuais usando medidas resumo, como a média a posteriori, a moda a posteriori ou a mediana a posteriori. Além disso, a distribuição a posteriori permite calcular intervalos de credibilidade para as estimativas dos parâmetros. Também é possível fazer previsões usando a distribuição a posteriori dos parâmetros, obtendo uma distribuição preditiva das categorias para novos dados.

A implementação da regressão bayesiana com variáveis de resposta multinomial em Python pode ser feita usando bibliotecas como PyMC3, Stan ou TensorFlow Probability, que fornecem ferramentas para modelagem bayesiana. Essas bibliotecas permitem especificar o modelo, estimar a distribuição a posteriori dos parâmetros e realizar previsões. O código pode variar dependendo da biblioteca escolhida, mas geralmente envolve a definição do modelo, a especificação das distribuições a priori e da verossimilhança, a amostragem da distribuição a posteriori e a análise dos resultados.

Aqui está um exemplo básico de regressão bayesiana com variáveis de resposta multinomial usando a biblioteca PyMC3:

import pymc3 as pm
import numpy as np

# Dados de entrada
X = np.array([[1, 2], [2, 3], [3, 4], [4, 5]])
y = np.array([0, 1, 2, 0])

# Definir modelo
with pm.Model() as model:
    # Priori para os coeficientes
    beta = pm.Normal('beta', mu=0, sd=1, shape=X.shape[1])
    # Verossimilhança multinomial
    p = pm.math.softmax(pm.math.dot(X, beta))
    likelihood = pm.Multinomial('likelihood', n=1, p=p, observed=y)

    # Amostragem da distribuição a posteriori
    trace = pm.sample(1000, tune=1000)

# Análise dos resultados
pm.summary(trace)

Neste exemplo, estamos realizando uma regressão bayesiana com variáveis de resposta multinomial simples.

Definimos distribuições normais como prioris para os coeficientes beta. Especificamos a verossimilhança multinomial para os dados observados y.

Através da amostragem da distribuição a posteriori usando a função sample do PyMC3, obtemos uma cadeia de amostras que representa a distribuição a posteriori dos coeficientes.

Por fim, podemos analisar os resultados usando a função summary do PyMC3 para obter estimativas dos coeficientes e suas incertezas.

É importante lembrar que a escolha das prioris, a especificação do modelo e a interpretação dos resultados são aspectos cruciais na regressão bayesiana com variáveis de resposta multinomial.

Além disso, a seleção adequada do tamanho da cadeia de amostras, a convergência da amostragem e a avaliação da adequação do modelo também são considerações importantes a serem feitas.

9.2.1.4 - Regressão Bayesiana Não Linear

A regressão bayesiana não linear é uma extensão da regressão bayesiana que permite modelar relações não lineares entre as variáveis independentes e a variável dependente.

Diferentemente da regressão linear, que assume uma relação linear entre as variáveis, a regressão não linear permite capturar relações mais complexas e não lineares, como curvas, interações não lineares e relações não monotônicas.

Na regressão bayesiana não linear, o objetivo é estimar a distribuição a posteriori dos parâmetros do modelo, que descrevem a relação entre as variáveis independentes e a variável dependente.

Esses parâmetros são tratados como variáveis aleatórias com distribuições a priori especificadas.

A distribuição a priori reflete o conhecimento ou as crenças iniciais sobre os parâmetros antes de observar os dados.

Para realizar a regressão bayesiana não linear, é necessário especificar as distribuições a priori para os parâmetros do modelo e a função de verossimilhança dos dados.

A função de verossimilhança captura a relação entre as variáveis independentes e a variável dependente, levando em consideração a natureza não linear do modelo. Geralmente, são utilizadas funções não lineares, como polinômios, funções exponenciais, logarítmicas, entre outras.

Uma vez que a distribuição a posteriori dos parâmetros é obtida, é possível fazer estimativas pontuais usando medidas resumo, como a média a posteriori, a moda a posteriori ou a mediana a posteriori.

Além disso, a distribuição a posteriori permite calcular intervalos de credibilidade para as estimativas dos parâmetros e realizar previsões para novos dados.

A implementação da regressão bayesiana não linear em Python pode ser feita usando bibliotecas como PyMC3, Stan ou TensorFlow Probability, que fornecem ferramentas para modelagem bayesiana.

Essas bibliotecas permitem especificar o modelo, estimar a distribuição a posteriori dos parâmetros e realizar previsões.

O código pode variar dependendo da biblioteca escolhida, mas geralmente envolve a definição do modelo, a especificação das distribuições a priori e da verossimilhança, a amostragem da distribuição a posteriori e a análise dos resultados.

É importante lembrar que a regressão bayesiana não linear pode ser computacionalmente intensiva, especialmente quando o modelo possui muitos parâmetros e/ou dados de tamanho grande.

Portanto, é importante considerar a capacidade computacional disponível e ajustar o modelo adequadamente para obter resultados confiáveis e eficientes.

A implementação da regressão bayesiana não linear em Python pode ser realizada utilizando a biblioteca PyMC3.

O PyMC3 fornece uma interface amigável para a modelagem bayesiana e a estimação da distribuição a posteriori dos parâmetros do modelo.

Aqui está um exemplo de código Python para a regressão bayesiana não linear utilizando PyMC3:

import pymc3 as pm
import numpy as np

# Dados de exemplo
x = np.linspace(0, 10, 100)
y = 2 * np.sin(x) + np.random.normal(0, 0.5, 100)

# Definição do modelo
with pm.Model() as model:
    # Priori para os parâmetros
    alpha = pm.Normal("alpha", mu=0, sd=1)
    beta = pm.Normal("beta", mu=0, sd=1)
    sigma = pm.HalfNormal("sigma", sd=1)
    
    # Modelo não linear
    mu = alpha + beta * np.sin(x)
    
    # Verossimilhança dos dados
    likelihood = pm.Normal("y", mu=mu, sd=sigma, observed=y)
    
    # Amostragem da distribuição a posteriori
    trace = pm.sample(1000, tune=1000)
    
# Análise dos resultados
sumario = pm.summary(trace)
print(sumario)

Nesse exemplo, estamos criando um modelo de regressão bayesiana não linear para ajustar uma curva senoidal aos dados de exemplo.

Definimos as distribuições a priori para os parâmetros alpha, beta e sigma. Em seguida, especificamos o modelo não linear utilizando a função seno e os parâmetros alpha e beta.

A verossimilhança dos dados é modelada como uma distribuição normal com média mu e desvio padrão sigma.

Por fim, realizamos a amostragem da distribuição a posteriori utilizando a função sample do PyMC3.

Após a amostragem, podemos analisar os resultados utilizando a função summary do PyMC3, que fornece uma visão geral dos parâmetros estimados, incluindo as estimativas pontuais, intervalos de credibilidade e outras estatísticas relevantes.

É importante ressaltar que a especificação do modelo e a escolha das distribuições a priori podem variar de acordo com o problema e o conhecimento prévio sobre os dados.

Portanto, é necessário ajustar o código de acordo com as necessidades específicas do problema em questão.

Os modelos hierárquicos e mistos são estruturas de modelagem estatística que permitem lidar com a complexidade e a heterogeneidade dos dados, incorporando diferentes níveis de variabilidade e correlação.

A seguir, são detalhados alguns dos tipos mais comuns de modelos hierárquicos e mistos:

• Modelos Hierárquicos Lineares: os modelos hierárquicos lineares, também conhecidos como modelos de efeitos mistos ou modelos de regressão com efeitos aleatórios, são utilizados quando os dados estão organizados em diferentes níveis hierárquicos, como indivíduos dentro de grupos ou observações repetidas ao longo do tempo. Esses modelos incorporam tanto efeitos fixos (que são comuns a todos os níveis) quanto efeitos aleatórios (que variam entre os níveis), permitindo modelar a heterogeneidade e a correlação entre as unidades de observação.
• Modelos de Mistura: os modelos de mistura são utilizados quando os dados são provenientes de diferentes subpopulações, e a distribuição dos dados pode ser descrita por uma combinação de distribuições de probabilidade. Cada subpopulação é representada por um componente do modelo, e os parâmetros podem variar entre os componentes. Os modelos de mistura são amplamente utilizados em análise de agrupamentos (clustering) e classificação, onde os dados podem ser melhor representados por diferentes grupos ou classes.
• Modelos de Sobrevivência Hierárquicos: os modelos de sobrevivência hierárquicos, também conhecidos como modelos de risco proporcional de Cox hierárquicos, são utilizados para analisar dados de tempo de vida ou dados de eventos recorrentes que estão organizados em diferentes níveis hierárquicos. Esses modelos permitem modelar a heterogeneidade entre os grupos e incorporar a estrutura de dependência entre as unidades de observação.
• Modelos de Espaço de Estados Hierárquicos: os modelos de espaço de estados hierárquicos são utilizados em análise de séries temporais para modelar a dinâmica de um sistema em diferentes níveis hierárquicos. Eles são compostos por um modelo de observação, que descreve a relação entre as observações e as variáveis latentes não observadas, e um modelo de transição, que descreve a evolução temporal dessas variáveis latentes. Esses modelos são úteis para capturar a heterogeneidade e a correlação entre as séries temporais observadas.

Esses são apenas alguns exemplos de modelos hierárquicos e mistos amplamente utilizados na modelagem estatística.

Cada tipo de modelo possui suas próprias características e aplicações específicas, e a escolha do modelo mais adequado depende da natureza dos dados e dos objetivos da análise.

9.4.1.1 - Modelos Hierárquicos Lineares

Os modelos hierárquicos lineares, também conhecidos como modelos lineares de efeitos mistos, são uma extensão dos modelos lineares tradicionais que permitem lidar com dados hierárquicos ou estruturados em diferentes níveis. Eles são amplamente utilizados em diversas áreas, como ciências sociais, educação, saúde e economia, para analisar dados que possuem uma estrutura de grupos aninhados.

Em um modelo hierárquico linear, os efeitos fixos e os efeitos aleatórios são combinados para capturar tanto as variações sistemáticas entre os grupos quanto as variações aleatórias dentro de cada grupo. Isso permite modelar a heterogeneidade dos dados e considerar a dependência entre as observações dentro dos grupos.

A estrutura básica de um modelo hierárquico linear pode ser definida da seguinte forma:

• Nível de grupo (níveis superiores):
• Variáveis preditoras (efeitos fixos) que explicam a variação sistemática entre os grupos.
• Parâmetros (hiperparâmetros) que capturam a variação aleatória entre os grupos.
• Nível de unidade (níveis inferiores):
• Variáveis preditoras (efeitos fixos) que explicam a variação sistemática dentro de cada grupo.
• Resíduos (efeitos aleatórios) que capturam a variação aleatória dentro de cada grupo.

A principal vantagem dos modelos hierárquicos lineares é que eles permitem estimar os efeitos fixos e aleatórios simultaneamente, levando em consideração a estrutura hierárquica dos dados. Isso resulta em estimativas mais precisas e interpretações mais corretas dos efeitos preditores.

Além disso, os modelos hierárquicos lineares também fornecem informações sobre a variação entre os grupos e a variação dentro dos grupos, permitindo uma análise mais detalhada da estrutura dos dados e da importância dos fatores de agrupamento.

A implementação de modelos hierárquicos lineares pode ser feita utilizando diversas bibliotecas estatísticas e de análise de dados, como o statsmodels e o lme4 em R. Essas bibliotecas fornecem funções e métodos específicos para ajustar e analisar modelos hierárquicos lineares, levando em consideração a estrutura hierárquica dos dados.

A escolha do modelo hierárquico linear adequado depende das características específicas dos dados e das perguntas de pesquisa. É importante considerar a estrutura dos dados, a quantidade de níveis hierárquicos, a natureza dos efeitos fixos e aleatórios, entre outros fatores, para selecionar o modelo mais apropriado.

É válido ressaltar que os modelos hierárquicos lineares podem ser estendidos para incluir diferentes distribuições de erros, como distribuições normais, binomiais, Poisson, entre outras, dependendo do tipo de variável resposta. Essa flexibilidade permite lidar com uma ampla gama de problemas e dados em diferentes áreas de pesquisa.

Para realizar a análise de Modelos Hierárquicos Lineares (ou Hierarchical Linear Models - HLM) em Python, você pode utilizar a biblioteca statsmodels. Os modelos hierárquicos lineares são usados para analisar dados hierárquicos, onde as observações estão agrupadas em diferentes níveis e podem ser afetadas tanto por variáveis do nível individual quanto por variáveis do nível superior.

Aqui está um exemplo de código para ajustar um Modelo Hierárquico Linear usando a biblioteca statsmodels:

import pandas as pd
import statsmodels.api as sm

# Criar um dataframe com os dados
data = pd.DataFrame({
    'variavel1': [1, 2, 3, 4, 5],
    'variavel2': [2, 4, 6, 8, 10],
    'variavel_dependente': [3, 6, 9, 12, 15],
    'grupo': ['A', 'A', 'B', 'B', 'B']
})

# Definir as variáveis independentes e dependentes
X = data[['variavel1', 'variavel2']]
y = data['variavel_dependente']

# Definir as variáveis de grupo
group = data['grupo']

# Adicionar intercepto às variáveis independentes
X = sm.add_constant(X)

# Ajustar o modelo hierárquico linear
model = sm.MixedLM(y, X, groups=group)
result = model.fit()

# Imprimir os resultados
print(result.summary())

Neste exemplo, o dataframe data é criado diretamente no código, com as variáveis independentes (variavel1 e variavel2), a variável dependente (variavel_dependente) e a variável de grupo (grupo).

O restante do código é semelhante ao exemplo anterior. As variáveis independentes são adicionadas um intercepto, o modelo hierárquico linear é ajustado utilizando a função MixedLM do statsmodels e os resultados são exibidos com print(result.summary()).

Certifique-se de ajustar o nome das colunas e os valores do dataframe de acordo com seus dados reais.

9.4.1.2 - Modelos de Mistura

Os modelos de mistura são uma classe de modelos estatísticos que são utilizados para modelar dados que são gerados a partir de uma mistura de diferentes distribuições. Eles são particularmente úteis quando os dados têm uma estrutura complexa e não podem ser facilmente modelados por uma única distribuição.

A ideia básica dos modelos de mistura é que os dados observados são uma combinação de várias subpopulações, cada uma seguindo uma distribuição probabilística específica. Cada subpopulação é chamada de componente da mistura e é caracterizada por seus próprios parâmetros, como média, variância e pesos de mistura.

Os modelos de mistura podem ser aplicados a diferentes tipos de variáveis, incluindo variáveis contínuas, categóricas e discretas. Dependendo do tipo de dados e das suposições sobre as distribuições das componentes, diferentes modelos de mistura podem ser utilizados. Alguns exemplos comuns incluem:

Modelos de Mistura Gaussiana: são utilizados quando se assume que cada componente da mistura segue uma distribuição gaussiana (normal). Esses modelos são amplamente utilizados em aplicações de análise de dados e podem ser estendidos para lidar com diferentes estruturas de covariância, como covariância diagonal, covariância esférica ou covariância completa.

Modelos de Mistura de Distribuições Categóricas: são utilizados quando as variáveis são categóricas, como dados de preferências ou classificações. Cada componente da mistura é modelado por uma distribuição categórica, que descreve a probabilidade de pertencer a cada categoria.

Modelos de Mistura de Poisson: são utilizados quando os dados são contagens ou eventos raros. Cada componente da mistura segue uma distribuição de Poisson, que descreve a taxa média de ocorrência dos eventos.

Modelos de Mistura de Bernoulli: são utilizados quando os dados são binários ou representam eventos de sucesso ou falha. Cada componente da mistura segue uma distribuição de Bernoulli, que descreve a probabilidade de sucesso.

Os modelos de mistura podem ser ajustados aos dados usando métodos de estimação, como o método da máxima verossimilhança ou o método de estimação de Bayes. A seleção do número de componentes da mistura é um desafio importante nesses modelos e pode ser abordada usando critérios estatísticos, como o critério de informação de Akaike (AIC) ou o critério de informação bayesiano (BIC).

Os modelos de mistura têm várias aplicações práticas, como segmentação de mercado, reconhecimento de padrões, agrupamento de dados e detecção de outliers. Eles são particularmente úteis quando os dados apresentam heterogeneidade não observada ou quando há sobreposição entre as diferentes subpopulações presentes nos dados.

Aqui está um exemplo de código em Python para ajustar um modelo de mistura utilizando a biblioteca Scikit-Learn:

from sklearn.mixture import GaussianMixture
import numpy as np

# Dados de exemplo
data = np.array([
    [1.2, 2.3],
    [0.5, 1.8],
    [2.4, 3.5],
    [0.8, 0.6],
    [2.0, 1.0]
])

# Ajustar o modelo de mistura
model = GaussianMixture(n_components=2)
model.fit(data)

# Prever as classes para novos dados
new_data = np.array([
    [1.0, 1.5],
    [2.2, 2.8]
])
pred = model.predict(new_data)

# Exibir os parâmetros estimados
print("Pesos dos componentes:", model.weights_)
print("Médias dos componentes:")
for i, mean in enumerate(model.means_):
    print(f"Componente {i+1}: {mean}")
print("Covariâncias dos componentes:")
for i, cov in enumerate(model.covariances_):
    print(f"Componente {i+1}: {cov}")

# Exibir as classes previstas para os novos dados
print("Classes previstas:", pred)

Pesos dos componentes: [0.6 0.4]
Médias dos componentes:
Componente 1: [1.36666667 2.53333333]
Componente 2: [1.4 0.8]
Covariâncias dos componentes:
Componente 1: [[0.61555656 0.55777778]
 [0.55777778 0.50888989]]
Componente 2: [[0.360001 0.12    ]
 [0.12     0.040001]]
Classes previstas: [0 0]

Lembre-se de adaptar o código aos seus dados específicos e ajustar os parâmetros do modelo de acordo com suas necessidades.

9.4.1.3 - Modelos de Sobrevivência Hierárquicos

Os modelos de sobrevivência hierárquicos são uma extensão dos modelos de sobrevivência padrão que permitem incorporar a estrutura hierárquica dos dados. Esses modelos são adequados para análise de dados de sobrevivência em que os indivíduos estão agrupados em clusters ou unidades de nível superior, como hospitais, escolas ou regiões geográficas.

A estrutura hierárquica nos dados de sobrevivência ocorre quando os indivíduos pertencem a grupos que compartilham características comuns e que podem influenciar o tempo até o evento de interesse. Por exemplo, em um estudo clínico multicêntrico, os pacientes podem ser agrupados por hospitais, e é esperado que os pacientes dentro de um mesmo hospital apresentem certa semelhança em relação ao tempo de sobrevivência. Os modelos de sobrevivência hierárquicos permitem levar em consideração essa estrutura hierárquica e estimar tanto os efeitos dos fatores individuais quanto os efeitos dos fatores de nível superior.

Os modelos de sobrevivência hierárquicos são geralmente formulados usando o modelo de riscos proporcionais de Cox como base. Nesse tipo de modelo, a função de risco é modelada como uma combinação linear das covariáveis individuais e covariáveis de nível superior, ponderadas pelos coeficientes correspondentes. Além disso, os modelos de sobrevivência hierárquicos podem incluir termos aleatórios para capturar a variação entre os grupos e permitir que os efeitos dos fatores de nível superior variem entre os grupos.

A estimação dos parâmetros nos modelos de sobrevivência hierárquicos é realizada usando métodos de máxima verossimilhança ou estimação bayesiana. A seleção do melhor modelo pode ser baseada em critérios de informação, como o critério de informação de Akaike (AIC) ou o critério de informação bayesiana (BIC), que levam em consideração a adequação do modelo e a penalização pela complexidade.

Os modelos de sobrevivência hierárquicos são úteis em muitas áreas de pesquisa, como estudos clínicos multicêntricos, estudos epidemiológicos com dados de sobrevivência agregados por regiões geográficas e estudos educacionais com alunos agrupados em escolas. Eles permitem explorar a estrutura hierárquica dos dados e fornecer estimativas mais precisas dos efeitos dos fatores individuais e de nível superior sobre a sobrevivência.

9.4.1.4 - Modelos de Espaço de Estados Hierárquicos

Os modelos de espaço de estados hierárquicos são uma extensão dos modelos de espaço de estados que permitem incorporar estruturas hierárquicas nos dados. Esses modelos são amplamente utilizados para analisar séries temporais que exibem uma organização hierárquica, onde as observações são agrupadas em diferentes níveis ou unidades.

A estrutura hierárquica nos dados de séries temporais ocorre quando as observações estão agrupadas em diferentes níveis, como regiões geográficas, setores de uma indústria, empresas ou indivíduos. Esses grupos podem exibir padrões de comportamento semelhantes que são influenciados por fatores de nível superior. Os modelos de espaço de estados hierárquicos permitem capturar essa estrutura hierárquica e estimar tanto os efeitos dos fatores individuais quanto os efeitos dos fatores de nível superior.

Nos modelos de espaço de estados hierárquicos, a série temporal em cada nível é modelada usando um modelo de espaço de estados padrão, que é composto por uma equação de transição e uma equação de observação. A equação de transição descreve a dinâmica temporal da série e a equação de observação relaciona a série temporal às variáveis observadas. Além disso, os modelos de espaço de estados hierárquicos incluem termos aleatórios para capturar a variação entre os grupos e permitir que os efeitos dos fatores de nível superior variem entre os grupos.

A estimação dos parâmetros nos modelos de espaço de estados hierárquicos é geralmente realizada usando métodos de máxima verossimilhança ou estimação bayesiana. A inferência sobre os estados ocultos e as previsões futuras também pode ser obtida usando métodos de filtragem e suavização, como o filtro de Kalman.

Os modelos de espaço de estados hierárquicos são amplamente utilizados em várias áreas, como economia, finanças, epidemiologia e meio ambiente. Eles permitem capturar a estrutura hierárquica nos dados de séries temporais e fornecer estimativas mais precisas dos efeitos dos fatores individuais e de nível superior. Esses modelos são úteis para análise e previsão de séries temporais em situações em que os dados exibem uma organização hierárquica e os efeitos dos fatores de nível superior são de interesse.

A análise de modelos de sobrevivência hierárquicos é uma área complexa e requer bibliotecas especializadas para sua implementação. Uma das bibliotecas populares para esse tipo de análise é o lifelines, que fornece ferramentas para ajustar modelos de sobrevivência em dados de natureza hierárquica.

Aqui está um exemplo básico de código em Python utilizando a biblioteca lifelines para ajustar um modelo de sobrevivência hierárquico:

from lifelines import CoxPHFitter
import pandas as pd

# Dados de exemplo
data = pd.DataFrame({
    'duration': [6, 9, 3, 7, 5],
    'event': [1, 1, 1, 0, 1],
    'group': [1, 1, 2, 2, 2],
    'covariate': [2, 4, 1, 3, 2]
})

# Ajustar o modelo de sobrevivência hierárquico
model = CoxPHFitter()
model.fit(data, duration_col='duration', event_col='event', cluster_col='group')

# Exibir os resultados do modelo
print(model.summary)

# Fazer previsões para novos dados
new_data = pd.DataFrame({
    'covariate': [3, 2],
    'group': [1, 2]
})
predictions = model.predict_survival_function(new_data)

# Exibir as previsões
for i, (idx, row) in enumerate(predictions.iterrows()):
    print(f"Grupo {idx}:")
    print(row)

                coef     exp(coef)  se(coef)  coef lower 95%  coef upper 95%  exp(coef) lower 95%  exp(coef) upper 95%  cmp to          z             p    -log2(p)
covariate                                                                                                                                                          
covariate -17.146909  3.574309e-08  0.814411      -18.743125      -15.550693         7.243762e-09         1.763681e-07     0.0 -21.054367  2.085494e-98  324.488564
Grupo 3.0:
0    1.0
1    1.0
Name: 3.0, dtype: float64
Grupo 5.0:
0    1.000000
1    0.606531
Name: 5.0, dtype: float64
Grupo 6.0:
0    1.00000
1    0.22313
Name: 6.0, dtype: float64
Grupo 7.0:
0    1.00000
1    0.22313
Name: 7.0, dtype: float64
Grupo 9.0:
0    0.0
1    0.0
Name: 9.0, dtype: float64

Neste exemplo, utilizamos a classe CoxPHFitter da biblioteca lifelines para ajustar um modelo de regressão de Cox em dados de sobrevivência hierárquicos.

Os dados de exemplo estão em um dataframe data, que inclui as colunas duration para a duração do evento, event para indicar se o evento ocorreu ou não, group para identificar os grupos hierárquicos e covariate como uma covariável.

Utilizamos o método fit para ajustar o modelo e podemos exibir os resultados resumidos com o atributo summary.

Além disso, podemos fazer previsões para novos dados utilizando o método predict_survival_function, fornecendo um dataframe new_data com as mesmas colunas utilizadas no ajuste do modelo.

Tenha em mente que esse é apenas um exemplo básico para ilustrar o uso da biblioteca lifelines em modelos de sobrevivência hierárquicos.

É importante adaptar o código de acordo com a estrutura específica dos seus dados e ajustar os parâmetros do modelo conforme necessário.

A inferência bayesiana não paramétrica é uma abordagem flexível que permite modelar de forma mais livre a distribuição dos dados, sem assumir uma forma paramétrica específica.

A seguir, detalho alguns dos tipos mais comuns de inferência bayesiana não paramétrica:

• Processos Gaussianos: os processos gaussianos são amplamente utilizados na inferência bayesiana não paramétrica para modelar funções contínuas. Eles são caracterizados por uma média e uma função de covariância, e a distribuição posterior é uma distribuição gaussiana condicional aos dados observados. Os processos gaussianos são frequentemente utilizados em regressão não paramétrica, krigagem (interpolção espacial) e em problemas de suavização de curvas.
• Processos de Dirichlet: os processos de Dirichlet são utilizados para modelar distribuições de probabilidade, especialmente em problemas de mistura e clustering. Eles permitem que a distribuição posterior seja uma distribuição de Dirichlet condicional aos dados observados. Os processos de Dirichlet são comumente utilizados em problemas de classificação, análise de agrupamentos e análise de tópicos.
• Processos de Dirichlet Multinomial: os processos de Dirichlet multinomial são uma extensão dos processos de Dirichlet e são utilizados para modelar distribuições multinomiais. Eles são especialmente úteis quando se deseja modelar dados categóricos ou de contagem. Os processos de Dirichlet multinomial são aplicados em problemas como modelagem de tópicos, análise de sentimentos e análise de redes.
• Processos de Dirichlet de Indian Buffet: os processos de Dirichlet de Indian Buffet são utilizados em problemas de modelagem de agrupamentos (clustering) com número variável de grupos. Eles são caracterizados pela metáfora de um buffet indiano, onde cada prato representa um grupo e cada cliente escolhe diferentes pratos. Esses processos permitem que a distribuição posterior seja uma combinação de distribuições de Dirichlet condicionais aos dados observados.

Esses são apenas alguns exemplos de inferência bayesiana não paramétrica, e existem muitas outras abordagens e modelos disponíveis.

A inferência bayesiana não paramétrica oferece flexibilidade na modelagem de dados complexos e é útil quando não se deseja fazer suposições rígidas sobre a distribuição dos dados.

A escolha do método adequado depende do tipo de dados, da estrutura do problema e dos objetivos da análise.

9.5.1.1 - Processos Gaussianos

Processos Gaussianos (Gaussian Processes) são uma classe de modelos probabilísticos que são amplamente utilizados em problemas de regressão, classificação e interpolação.

Eles são particularmente úteis quando não se assume uma distribuição específica para os dados, mas sim uma função de distribuição conjunta multivariada entre as variáveis de entrada e saída.

A principal característica dos processos Gaussianos é que eles definem uma distribuição conjunta multivariada sobre um conjunto de variáveis aleatórias, em que qualquer subconjunto finito dessas variáveis tem uma distribuição gaussiana condicional.

Isso significa que, em vez de modelar diretamente uma função específica, o processo Gaussiano modela a distribuição sobre as funções possíveis que se encaixam nos dados observados.

Em um processo Gaussiano, a distribuição conjunta é especificada por uma média zero e uma matriz de covariância que captura a relação entre as diferentes observações.

A escolha da função de covariância é crucial, pois ela determina como as observações se correlacionam entre si.

Funções de covariância comuns incluem a função exponencial, função RBF (Radial Basis Function) e a função Matern.

Os processos Gaussianos podem ser usados para fazer previsões e inferências em novos pontos, dadas as observações existentes.

A previsão é feita calculando-se a média e a covariância condicional do processo Gaussiano nos novos pontos.

Essa propriedade é particularmente útil em problemas de regressão, em que se deseja estimar um valor contínuo com incerteza associada.

A aplicação dos processos Gaussianos envolve a estimação dos hiperparâmetros da função de covariância, que são otimizados para melhor se ajustar aos dados observados.

Existem várias abordagens para a estimação desses hiperparâmetros, incluindo a máxima verossimilhança e a inferência Bayesiana.

A biblioteca Scikit-Learn oferece suporte à implementação de processos Gaussianos por meio da classe GaussianProcessRegressor para problemas de regressão e da classe GaussianProcessClassifier para problemas de classificação.

Essas classes fornecem métodos para ajustar o modelo aos dados observados, fazer previsões em novos pontos e avaliar a incerteza associada às previsões.

É importante destacar que a aplicação de processos Gaussianos pode ser computacionalmente intensiva, especialmente para grandes conjuntos de dados.

Portanto, é necessário considerar a escalabilidade e o desempenho ao lidar com problemas de maior complexidade.

No geral, os processos Gaussianos oferecem uma abordagem flexível e probabilística para modelagem de dados, permitindo a captura de incerteza nas previsões e fornecendo uma base sólida para inferências estatísticas.

Eles são amplamente utilizados em várias áreas, incluindo aprendizado de máquina, estatística, processamento de sinais e otimização.

A modelagem de Processos Gaussianos é uma abordagem estatística que permite modelar e prever funções suaves ou curvas a partir de dados observados.

Os Processos Gaussianos são uma extensão dos modelos lineares, mas em vez de assumir uma relação linear entre as variáveis, eles permitem a modelagem de relações não lineares.

A biblioteca Scikit-Learn fornece uma implementação dos Processos Gaussianos em Python.

Abaixo está um exemplo de código que mostra como usar o GaussianProcessRegressor do Scikit-Learn para ajustar um processo gaussiano aos dados e fazer previsões.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF

# Dados de treinamento
X_train = np.array([[1], [2], [3], [4], [5]])
y_train = np.array([1, 3, 2, 4, 3])

# Definir o modelo de processo gaussiano
kernel = RBF(length_scale=1.0)  # Kernel RBF com escala de comprimento 1.0
model = GaussianProcessRegressor(kernel=kernel)

# Ajustar o modelo aos dados de treinamento
model.fit(X_train, y_train)

# Dados de teste para fazer previsões
X_test = np.array([[1.5], [2.5], [3.5], [4.5]])
y_test = np.array([0, 0, 0, 0])  # Valor de y para os pontos de teste (apenas para ilustração)

# Fazer previsões com o modelo ajustado
y_pred, sigma = model.predict(X_test, return_std=True)

# Plotar os dados de treinamento, dados de teste e previsões
plt.scatter(X_train, y_train, color='red', label='Dados de treinamento')
plt.scatter(X_test, y_test, color='blue', label='Dados de teste')
plt.plot(X_test, y_pred, color='green', label='Previsões')
plt.fill_between(X_test.flatten(), y_pred - 2 * sigma, y_pred + 2 * sigma, color='gray', alpha=0.2, label='Incerteza')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()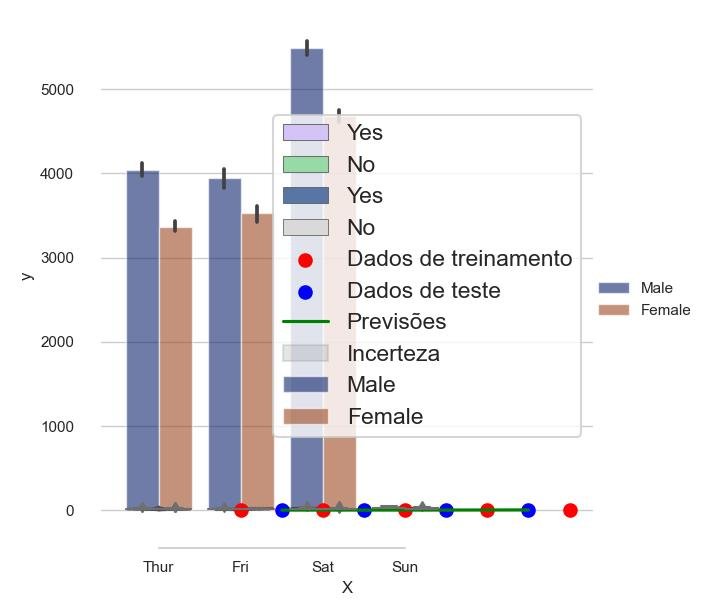

Neste exemplo, criamos uma instância do GaussianProcessRegressor com um kernel RBF (Função de Base Radial) com uma escala de comprimento de 1.0.

Ajustamos o modelo aos dados de treinamento (X_train e y_train) e, em seguida, usamos o modelo para fazer previsões nos dados de teste (X_test).

A função predict retorna as previsões (y_pred) e o desvio padrão (sigma) para cada ponto de teste.

Finalmente, plotamos os dados de treinamento, os dados de teste, as previsões e a incerteza associada às previsões.

Os Processos Gaussianos são úteis quando se deseja modelar funções suaves ou curvas a partir de dados e obter estimativas de incerteza associadas às previsões.

Eles podem ser aplicados em diversas áreas, como previsão de séries temporais, otimização de hiperparâmetros, aprendizado por reforço e muito mais.

9.5.1.2 - Processos de Dirichlet

Processos de Dirichlet (Dirichlet Processes) são uma classe de modelos probabilísticos utilizados principalmente em problemas de agrupamento não paramétrico, ou seja, problemas em que o número de grupos/clusters é desconhecido a priori e pode variar de acordo com os dados.

Esses processos são baseados na distribuição de Dirichlet e têm propriedades únicas que permitem a geração de distribuições de probabilidade flexíveis e adaptáveis.

O processo de Dirichlet é definido em um espaço de medida e é caracterizado por dois parâmetros principais: uma medida base e um parâmetro de concentração.

A medida base especifica a distribuição inicial dos grupos e o parâmetro de concentração controla a tendência do processo de gerar novos grupos.

Quanto maior o parâmetro de concentração, mais agrupamentos serão gerados.

A principal aplicação dos processos de Dirichlet é em problemas de agrupamento, em que se deseja atribuir objetos a grupos com base em suas características.

A principal vantagem desses processos é a capacidade de modelar automaticamente o número de grupos, sem a necessidade de especificar um valor fixo a priori.

Isso torna os processos de Dirichlet particularmente úteis em cenários onde o número de grupos pode variar ou não é conhecido antecipadamente.

Uma das variantes mais comuns dos processos de Dirichlet é o processo de Dirichlet de restaurantes chineses (Chinese Restaurant Process - CRP).

Nesse processo, cada objeto é alocado a um grupo existente com uma probabilidade proporcional ao número de objetos já alocados a esse grupo.

Caso contrário, um novo grupo é criado e o objeto é alocado a esse novo grupo.

Esse processo é chamado de "Restaurante Chinês" devido à analogia de clientes que entram em um restaurante e escolhem uma mesa existente ou abrem uma nova mesa.

A biblioteca Scikit-Learn não possui uma implementação direta dos processos de Dirichlet, mas existem bibliotecas específicas, como o pyMC3 e o Edward, que oferecem suporte a esses modelos.

Essas bibliotecas fornecem funções para criar e inferir modelos de processos de Dirichlet, bem como realizar amostragem posterior para obter distribuições de probabilidade a posteriori dos parâmetros do modelo.

Os processos de Dirichlet são particularmente úteis em problemas de agrupamento não paramétrico, nos quais o número de grupos é desconhecido ou variável.

Eles fornecem uma abordagem flexível e adaptável para modelagem de dados, permitindo a descoberta automática de estruturas de agrupamento e acomodando uma ampla gama de cenários de dados.

Os Processos de Dirichlet são modelos probabilísticos que são usados para modelar distribuições de probabilidade sobre variáveis aleatórias que representam proporções.

Eles são frequentemente usados em problemas de mistura de distribuições, onde cada componente da mistura é representado por uma variável aleatória com uma distribuição de Dirichlet associada.

A biblioteca scipy oferece suporte ao cálculo com Processos de Dirichlet em Python.

No entanto, a implementação específica pode depender da aplicação específica que você está considerando.

Aqui está um exemplo de código que ilustra o uso do módulo dirichlet do scipy para gerar uma distribuição de Dirichlet e amostrar a partir dela:

import numpy as np
from scipy.stats import dirichlet

# Parâmetros da distribuição de Dirichlet
alpha = [1, 2, 3]

# Gerar uma distribuição de Dirichlet
dist = dirichlet(alpha)

# Amostrar a partir da distribuição de Dirichlet
samples = dist.rvs(size=100)

# Imprimir as amostras
print(samples)

[[1.36115284e-01 3.61248151e-01 5.02636565e-01]
 [2.89440258e-01 1.93739343e-02 6.91185808e-01]
 [6.85284292e-02 4.02731631e-01 5.28739940e-01]
 [2.93611325e-01 2.68808580e-01 4.37580095e-01]
 [3.67672161e-01 3.45028005e-01 2.87299834e-01]
 [3.49964762e-01 3.78276698e-01 2.71758540e-01]
 [5.69581720e-01 3.29898404e-01 1.00519876e-01]
 [4.45063376e-02 5.73027778e-01 3.82465885e-01]
 [2.43868969e-02 4.32513959e-01 5.43099144e-01]
 [1.69090968e-01 2.83175895e-01 5.47733137e-01]
 [8.79472299e-02 1.10323931e-01 8.01728840e-01]
 [2.97920220e-01 1.27953503e-01 5.74126277e-01]
 [2.01289901e-02 7.37007258e-01 2.42863752e-01]
 [3.72685053e-01 2.37329441e-01 3.89985506e-01]
 [4.12698046e-02 4.75307891e-01 4.83422304e-01]
 [2.07041979e-01 5.23325770e-01 2.69632251e-01]
 [1.53291191e-01 6.26552927e-01 2.20155882e-01]
 [6.89192413e-02 6.04357403e-01 3.26723356e-01]
 [9.20226160e-02 4.51358713e-01 4.56618671e-01]
 [2.22162016e-01 2.41429394e-01 5.36408590e-01]
 [2.28892541e-01 2.10057088e-01 5.61050372e-01]
 [4.68800881e-01 3.93912061e-01 1.37287057e-01]
 [1.63740264e-01 2.67625121e-01 5.68634615e-01]
 [1.58647153e-01 2.58354156e-01 5.82998690e-01]
 [1.12291977e-01 1.88533384e-01 6.99174639e-01]
 [7.45386972e-02 1.02844545e-01 8.22616758e-01]
 [2.60021609e-04 9.11185571e-01 8.85544077e-02]
 [1.18486698e-01 3.79259952e-01 5.02253350e-01]
 [4.04941945e-01 2.66588402e-01 3.28469654e-01]
 [1.98150177e-02 8.50148631e-01 1.30036351e-01]
 [3.71022921e-02 2.25010163e-01 7.37887545e-01]
 [1.16765738e-01 2.31838827e-01 6.51395434e-01]
 [1.54897277e-01 1.42403516e-01 7.02699207e-01]
 [1.70272029e-01 3.93482989e-01 4.36244983e-01]
 [2.78169863e-01 2.66915662e-01 4.54914476e-01]
 [3.07070563e-01 4.49430170e-01 2.43499267e-01]
 [2.45765376e-01 2.05477125e-01 5.48757499e-01]
 [2.97338986e-03 6.46346919e-01 3.50679691e-01]
 [4.74949556e-01 2.01438331e-01 3.23612113e-01]
 [4.94057688e-02 3.27780790e-01 6.22813441e-01]
 [2.27111237e-01 4.22278794e-01 3.50609969e-01]
 [4.13545638e-01 3.53354758e-01 2.33099605e-01]
 [2.46206252e-01 2.77736404e-01 4.76057345e-01]
 [4.14502533e-02 3.32436466e-01 6.26113281e-01]
 [2.00697331e-01 1.09235525e-01 6.90067144e-01]
 [1.43196152e-02 1.41632130e-01 8.44048255e-01]
 [3.67909549e-01 2.83166567e-01 3.48923884e-01]
 [2.35180380e-01 1.84125515e-01 5.80694104e-01]
 [6.46716938e-02 1.37748893e-01 7.97579413e-01]
 [1.75239602e-02 5.04757986e-01 4.77718054e-01]
 [9.54202749e-02 3.63561848e-01 5.41017878e-01]
 [7.26045115e-02 7.23935537e-01 2.03459952e-01]
 [7.92067433e-02 1.08894577e-01 8.11898680e-01]
 [7.28934571e-02 7.42271055e-01 1.84835487e-01]
 [1.68755300e-01 2.83374920e-01 5.47869780e-01]
 [2.09625550e-01 4.80228145e-01 3.10146305e-01]
 [8.97039942e-02 4.78733610e-01 4.31562396e-01]
 [2.11542302e-02 3.69602718e-01 6.09243052e-01]
 [2.83312939e-02 5.13552053e-01 4.58116653e-01]
 [1.57760233e-02 2.59960244e-02 9.58227952e-01]
 [1.99028666e-01 6.48894118e-01 1.52077215e-01]
 [7.12668767e-02 1.73086438e-01 7.55646685e-01]
 [6.52640181e-03 3.36086536e-01 6.57387063e-01]
 [1.47084129e-01 5.74905643e-01 2.78010228e-01]
 [3.58433858e-02 6.41832370e-01 3.22324244e-01]
 [7.72172538e-02 4.94861630e-01 4.27921116e-01]
 [3.49026275e-01 2.62452886e-01 3.88520839e-01]
 [1.92209921e-02 2.66871436e-01 7.13907572e-01]
 [1.76100771e-03 4.49227158e-01 5.49011834e-01]
 [3.69841235e-01 2.28433080e-01 4.01725685e-01]
 [1.27884290e-01 2.48950427e-01 6.23165283e-01]
 [1.87084624e-01 2.65145957e-01 5.47769419e-01]
 [1.24058960e-01 1.91450223e-01 6.84490817e-01]
 [1.75253926e-01 5.82327092e-01 2.42418982e-01]
 [3.42723431e-03 8.03717365e-01 1.92855401e-01]
 [4.66811876e-01 1.42747100e-01 3.90441025e-01]
 [8.25085495e-03 4.04058506e-01 5.87690639e-01]
 [5.14853071e-03 1.58787543e-01 8.36063926e-01]
 [1.39297534e-01 5.06330057e-01 3.54372410e-01]
 [3.23955535e-01 2.37271313e-01 4.38773151e-01]
 [1.95021881e-01 2.42448237e-01 5.62529881e-01]
 [3.91083753e-01 1.82038633e-01 4.26877614e-01]
 [1.75615341e-01 4.78235392e-01 3.46149267e-01]
 [3.03524793e-01 2.00066871e-01 4.96408336e-01]
 [7.72126557e-02 1.96312831e-01 7.26474513e-01]
 [4.74864668e-01 2.02389508e-01 3.22745823e-01]
 [6.09162513e-03 6.45548486e-01 3.48359889e-01]
 [7.00205753e-01 9.11551613e-02 2.08639086e-01]
 [2.68634508e-02 4.47889629e-01 5.25246920e-01]
 [1.12928224e-01 2.44260921e-01 6.42810855e-01]
 [1.11314755e-01 6.98037218e-01 1.90648027e-01]
 [2.50502338e-01 5.65833083e-01 1.83664580e-01]
 [3.48219672e-01 2.69896607e-02 6.24790668e-01]
 [2.51256549e-01 2.08681208e-01 5.40062243e-01]
 [5.01002189e-02 4.56024984e-01 4.93874797e-01]
 [3.47020887e-02 4.50860487e-01 5.14437424e-01]
 [2.99595161e-03 2.55672330e-01 7.41331718e-01]
 [8.35454291e-02 6.28479387e-01 2.87975184e-01]
 [1.17483793e-01 2.89991191e-01 5.92525016e-01]
 [1.94809133e-02 2.53355962e-01 7.27163125e-01]]

Neste exemplo, definimos os parâmetros da distribuição de Dirichlet como alpha = [1, 2, 3].

Em seguida, criamos uma instância da distribuição de Dirichlet usando dirichlet(alpha).

Usamos o método rvs para amostrar 100 pontos a partir da distribuição de Dirichlet.

As amostras são armazenadas na matriz samples e impressas na saída.

Este é apenas um exemplo básico para ilustrar como gerar amostras de uma distribuição de Dirichlet usando o scipy.

Dependendo da aplicação específica, podem ser necessários ajustes adicionais nos parâmetros e nas etapas de processamento dos dados.

9.5.1.3 - Processos de Dirichlet Multinomial

Os Processos de Dirichlet Multinomial (Dirichlet Multinomial Processes - DMPs) são uma extensão dos Processos de Dirichlet para problemas de agrupamento em dados categóricos, nos quais as variáveis de interesse são de natureza discreta e não contínua.

Eles são frequentemente aplicados em problemas de agrupamento de dados textuais, análise de tópicos e classificação de documentos.

Enquanto o Processo de Dirichlet modela a distribuição de probabilidade sobre as probabilidades de um vetor multinomial, o DMP modela a distribuição de probabilidade sobre as distribuições de probabilidade de um vetor multinomial.

Isso permite que o DMP capture a incerteza em torno das probabilidades dos diferentes estados categóricos e forneça uma maneira flexível de modelar agrupamentos em dados categóricos.

Assim como nos Processos de Dirichlet, os DMPs são definidos por uma medida base e um parâmetro de concentração.

A medida base especifica a distribuição inicial das probabilidades dos estados categóricos, enquanto o parâmetro de concentração controla a tendência do processo de gerar novas distribuições.

Um alto valor de concentração resulta em agrupamentos mais específicos, enquanto um valor baixo de concentração leva a agrupamentos mais difusos.

A inferência em DMPs envolve a estimação da distribuição a posteriori das distribuições de probabilidade dos estados categóricos para cada grupo.

Isso pode ser realizado usando técnicas de amostragem estocástica, como a amostragem de Gibbs ou a amostragem de Monte Carlo via cadeias de Markov (MCMC).

Essas técnicas permitem obter uma estimativa da distribuição a posteriori dos parâmetros do modelo e, consequentemente, realizar inferências sobre os agrupamentos.

A implementação direta de DMPs pode exigir algoritmos computacionalmente intensivos, especialmente para grandes conjuntos de dados categóricos.

Portanto, é recomendável utilizar bibliotecas especializadas em aprendizado de máquina probabilístico, como o pyMC3 e o Edward, que fornecem ferramentas e métodos eficientes para a inferência de DMPs.

Os Processos de Dirichlet Multinomial são uma abordagem poderosa para modelar agrupamentos em dados categóricos.

Eles permitem a descoberta automática de agrupamentos e acomodam a incerteza nas probabilidades dos diferentes estados categóricos.

Esses modelos são amplamente utilizados em problemas de agrupamento de texto, classificação de documentos e análise de tópicos, fornecendo uma maneira flexível de entender a estrutura dos dados categóricos.

O processo de Dirichlet Multinomial é um modelo probabilístico que combina o Processo de Dirichlet com a distribuição multinomial.

Ele é usado para modelar a distribuição conjunta de várias variáveis aleatórias discretas, onde cada variável segue uma distribuição multinomial condicionada a uma distribuição de Dirichlet.

A biblioteca scipy não possui uma implementação específica para o Processo de Dirichlet Multinomial.

No entanto, você pode implementar seu próprio código para amostrar a partir dessa distribuição usando a função dirichlet do scipy.stats e a função multinomial do numpy.random.

Aqui está um exemplo de código que ilustra como gerar amostras a partir de um Processo de Dirichlet Multinomial:

import numpy as np
from scipy.stats import dirichlet, multinomial

# Definir os parâmetros do processo de Dirichlet Multinomial
alpha = np.array([1, 2, 3])  # Parâmetros de concentração da distribuição Dirichlet
n_samples = 100  # Número de amostras a serem geradas

# Gerar amostras do processo de Dirichlet Multinomial
dirichlet_samples = dirichlet.rvs(alpha, size=n_samples)
multinomial_samples = [multinomial.rvs(1, p) for p in dirichlet_samples]

# Imprimir as amostras geradas
for i, sample in enumerate(multinomial_samples):
    print(f"Amostra {i+1}: {sample}")

Amostra 1: [0 1 0]
Amostra 2: [0 0 1]
Amostra 3: [1 0 0]
Amostra 4: [0 1 0]
Amostra 5: [0 0 1]
Amostra 6: [0 0 1]
Amostra 7: [1 0 0]
Amostra 8: [0 1 0]
Amostra 9: [0 1 0]
Amostra 10: [0 0 1]
Amostra 11: [0 0 1]
Amostra 12: [0 0 1]
Amostra 13: [0 0 1]
Amostra 14: [0 1 0]
Amostra 15: [0 1 0]
Amostra 16: [1 0 0]
Amostra 17: [0 1 0]
Amostra 18: [0 1 0]
Amostra 19: [0 0 1]
Amostra 20: [0 0 1]
Amostra 21: [0 0 1]
Amostra 22: [1 0 0]
Amostra 23: [0 0 1]
Amostra 24: [0 0 1]
Amostra 25: [0 0 1]
Amostra 26: [0 0 1]
Amostra 27: [1 0 0]
Amostra 28: [0 0 1]
Amostra 29: [0 0 1]
Amostra 30: [0 1 0]
Amostra 31: [0 0 1]
Amostra 32: [0 0 1]
Amostra 33: [1 0 0]
Amostra 34: [0 0 1]
Amostra 35: [1 0 0]
Amostra 36: [0 0 1]
Amostra 37: [0 0 1]
Amostra 38: [0 0 1]
Amostra 39: [0 1 0]
Amostra 40: [1 0 0]
Amostra 41: [1 0 0]
Amostra 42: [0 0 1]
Amostra 43: [0 1 0]
Amostra 44: [0 1 0]
Amostra 45: [0 0 1]
Amostra 46: [1 0 0]
Amostra 47: [1 0 0]
Amostra 48: [0 0 1]
Amostra 49: [0 1 0]
Amostra 50: [1 0 0]
Amostra 51: [0 0 1]
Amostra 52: [0 0 1]
Amostra 53: [0 0 1]
Amostra 54: [0 0 1]
Amostra 55: [1 0 0]
Amostra 56: [0 0 1]
Amostra 57: [0 0 1]
Amostra 58: [1 0 0]
Amostra 59: [1 0 0]
Amostra 60: [0 0 1]
Amostra 61: [0 1 0]
Amostra 62: [0 0 1]
Amostra 63: [0 0 1]
Amostra 64: [0 1 0]
Amostra 65: [0 1 0]
Amostra 66: [0 0 1]
Amostra 67: [0 1 0]
Amostra 68: [0 1 0]
Amostra 69: [0 1 0]
Amostra 70: [0 0 1]
Amostra 71: [1 0 0]
Amostra 72: [0 0 1]
Amostra 73: [0 1 0]
Amostra 74: [0 0 1]
Amostra 75: [0 1 0]
Amostra 76: [0 0 1]
Amostra 77: [0 0 1]
Amostra 78: [0 1 0]
Amostra 79: [0 0 1]
Amostra 80: [0 0 1]
Amostra 81: [0 0 1]
Amostra 82: [0 1 0]
Amostra 83: [0 1 0]
Amostra 84: [0 1 0]
Amostra 85: [0 0 1]
Amostra 86: [1 0 0]
Amostra 87: [1 0 0]
Amostra 88: [0 0 1]
Amostra 89: [0 0 1]
Amostra 90: [0 1 0]
Amostra 91: [0 1 0]
Amostra 92: [0 0 1]
Amostra 93: [0 0 1]
Amostra 94: [0 0 1]
Amostra 95: [0 1 0]
Amostra 96: [0 0 1]
Amostra 97: [1 0 0]
Amostra 98: [0 0 1]
Amostra 99: [0 1 0]
Amostra 100: [0 1 0]

Neste exemplo, definimos os parâmetros da distribuição de Dirichlet como alpha = [1, 2, 3].

Especificamos o número de variáveis aleatórias como num_variables e o número de amostras a serem geradas como num_samples.

Em seguida, criamos uma instância da distribuição de Dirichlet usando dirichlet.rvs(alpha).

Usamos um loop para gerar amostras a partir do processo de Dirichlet Multinomial, onde cada amostra é uma matriz binária indicando a presença ou ausência de cada variável aleatória.

As amostras são armazenadas na matriz samples e impressas na saída.

Lembre-se de que este é apenas um exemplo básico para ilustrar como gerar amostras a partir de um Processo de Dirichlet Multinomial.

Dependendo da aplicação específica, podem ser necessários ajustes adicionais nos parâmetros e nas etapas de processamento dos dados.

9.5.1.4 - Processos de Dirichlet de Indian Buffet

Os Processos de Dirichlet de Indian Buffet (Indian Buffet Process - IBP) são um tipo de processo estocástico não paramétrico utilizado em problemas de aprendizado de máquina probabilístico.

Eles foram propostos por Griffiths e Ghahramani em 2006 como uma abordagem flexível para modelar problemas de agrupamento de dados com características latentes.

O IBP é inspirado pelo processo de autoatendimento em um buffet indiano, onde os clientes selecionam pratos de uma variedade infinita de opções.

No contexto do IBP, cada prato representa uma característica latente (ou seja, uma variável oculta) e cada cliente representa uma amostra do conjunto de dados.

Cada cliente "se serve" do buffet e seleciona um número variável de pratos (características latentes), criando assim uma representação única dos pratos selecionados.

A principal ideia do IBP é que a matriz de características latentes seja uma matriz esparsa, ou seja, cada amostra seleciona apenas um subconjunto das características disponíveis.

Isso permite que o modelo capture a variabilidade nos padrões de presença/ausência das características latentes nas amostras.

A definição matemática do IBP envolve a utilização de um processo de Poisson para modelar o número de pratos selecionados por cada cliente e um processo de Bernoulli para modelar a presença ou ausência de cada prato em cada amostra.

Através de uma série de etapas de amostragem estocástica, é possível inferir a distribuição a posteriori dos pratos selecionados por cada amostra, bem como a matriz de características latentes como um todo.

Os Processos de Dirichlet de Indian Buffet têm várias aplicações em aprendizado de máquina, incluindo a modelagem de tópicos em texto, agrupamento de documentos, análise de imagens e muito mais.

Eles oferecem uma maneira flexível de capturar a estrutura latente dos dados e permitem a descoberta automática de padrões relevantes.

A inferência em modelos IBP pode ser realizada usando técnicas de amostragem estocástica, como a amostragem de Gibbs ou a amostragem de Monte Carlo via cadeias de Markov (MCMC).

Existem implementações disponíveis em bibliotecas de aprendizado de máquina probabilístico, como o pyMC3 e o Edward.

O processo de Dirichlet de Indian Buffet é um modelo estatístico que descreve a alocação não paramétrica de objetos a recursos.

Aqui está um exemplo de código Python para simular o processo de Dirichlet de Indian Buffet:

import numpy as np
from scipy.stats import beta

def indian_buffet_process(alpha, num_objects):
    # Inicialização
    Z = np.zeros((num_objects, num_objects), dtype=int)
    m = np.zeros(num_objects, dtype=int)
    pi = np.zeros(num_objects)
    
    # Primeiro objeto escolhe o número de pratos
    m[0] = np.random.poisson(alpha)
    Z[0, :m[0]] = 1
    pi[:m[0]] = beta.rvs(1, alpha, size=m[0])
    
    # Gerar atributos para os objetos subsequentes
    for i in range(1, num_objects):
        for j in range(m[i-1]):
            prob = np.sum(Z[:i, j]) / i
            if np.random.rand() < prob:
                Z[i, j] = 1
        m[i] = np.random.poisson(alpha / (i + 1))
        if m[i] > m[i-1]:
            pi[m[i-1]:m[i]] = beta.rvs(1, alpha, size=m[i] - m[i-1])
    
    return Z, pi

# Parâmetros do processo de Dirichlet de Indian Buffet
alpha = 2  # Hiperparâmetro de concentração
num_objects = 10  # Número de objetos a serem gerados

# Simular o processo de Dirichlet de Indian Buffet
Z, pi = indian_buffet_process(alpha, num_objects)

# Imprimir os resultados
print("Matriz de atributos Z:")
print(Z)
print("Probabilidades pi:")
print(pi)

Matriz de atributos Z:
[[1 1 1 0 0 0 0 0 0 0]
 [1 1 1 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0]]
Probabilidades pi:
[0.71861974 0.13746001 0.69342938 0.         0.         0.
 0.         0.         0.         0.        ]

Este código simula o processo de Dirichlet de Indian Buffet para gerar uma matriz de atributos Z, onde cada linha representa um objeto e cada coluna representa um atributo.

Os atributos são binários, com 1 indicando que o objeto possui o atributo e 0 indicando que não possui.

A matriz de probabilidades pi indica as probabilidades associadas a cada atributo.

Os modelos de mistura e clustering bayesiano são técnicas estatísticas que permitem agrupar dados em subpopulações não observadas com base em suas características.

Eles são chamados de "bayesianos" porque utilizam a abordagem bayesiana para inferência estatística.

Em geral, os modelos de mistura e clustering bayesiano assumem que os dados são gerados por uma mistura de distribuições de probabilidade.

Cada subpopulação é representada por uma distribuição de probabilidade específica, e a atribuição de cada dado a uma subpopulação é modelada como uma variável latente.

A abordagem bayesiana permite incorporar incertezas sobre os parâmetros do modelo e sobre a atribuição de cada dado a uma subpopulação.

Isso é feito especificando distribuições a priori para os parâmetros do modelo e, em seguida, atualizando essas distribuições com base nos dados observados usando o teorema de Bayes.

Existem várias técnicas para implementar modelos de mistura e clustering bayesiano.

Alguns exemplos comuns incluem:

• Modelos de Mistura de Dirichlet: Esses modelos assumem que as subpopulações são distribuições de probabilidade extraídas de uma distribuição de Dirichlet. O número de subpopulações pode ser fixo ou pode ser inferido automaticamente do dado.
• Modelos de Mistura Gaussianas: Esses modelos assumem que as subpopulações são distribuições Gaussianas. Cada subpopulação é caracterizada por sua média e matriz de covariância.
• Modelos de Clusterização Hierárquica: Esses modelos constroem uma hierarquia de subpopulações, onde cada subpopulação pode conter subpopulações menores.

Isso permite uma representação mais flexível da estrutura de agrupamento dos dados.

Modelos de Clusterização por Processos Gaussianos: Esses modelos assumem que os dados são gerados por uma mistura de processos Gaussianos, onde cada processo representa uma subpopulação.

A estrutura de agrupamento é determinada de forma não paramétrica, permitindo que o número de subpopulações seja aprendido a partir dos dados.

A inferência em modelos de mistura e clustering bayesiano é geralmente realizada usando métodos de amostragem Markov Chain Monte Carlo (MCMC), como o Metropolis-Hastings ou o Gibbs sampler.

Esses métodos permitem explorar a distribuição posterior dos parâmetros e das atribuições latentes de forma eficiente.

Em resumo, os modelos de mistura e clustering bayesiano são poderosas ferramentas para a análise de dados não rotulados e podem ser aplicados em uma ampla variedade de áreas, incluindo reconhecimento de padrões, segmentação de imagens, análise de dados genômicos, entre outros.

Eles fornecem uma maneira flexível de modelar e explorar a estrutura subjacente nos dados, permitindo a descoberta de subpopulações e a obtenção de insights valiosos.

9.6.1.1 - Modelos de Mistura de Dirichlet

Os modelos de Mistura de Dirichlet são uma classe de modelos probabilísticos utilizados para modelar dados que são provenientes de uma mistura de subpopulações não observadas.

Esses modelos são amplamente utilizados em várias áreas, incluindo aprendizado de máquina, análise de dados, reconhecimento de padrões e clustering.

O modelo de Mistura de Dirichlet assume que os dados são gerados a partir de uma mistura de distribuições de probabilidade, onde cada subpopulação é representada por uma distribuição específica.

Essas distribuições podem ser de qualquer tipo, como Gaussianas, Poisson, exponenciais, entre outras, dependendo da natureza dos dados.

Os modelos de Mistura de Dirichlet são chamados assim porque usam a distribuição de Dirichlet como priori para as proporções de mistura.

A distribuição de Dirichlet é uma distribuição de probabilidade multivariada que descreve a distribuição de probabilidades sobre proporções.

A inferência em modelos de Mistura de Dirichlet envolve a estimação dos parâmetros das distribuições de probabilidade de cada subpopulação, bem como a determinação das proporções de mistura.

Existem várias abordagens para realizar essa inferência, incluindo métodos de otimização, métodos de amostragem Markov Chain Monte Carlo (MCMC) e métodos de estimação bayesiana.

Uma vez que os parâmetros do modelo são estimados, é possível realizar várias análises e inferências, tais como a classificação de novos dados em subpopulações, a estimativa das proporções de mistura em uma amostra e a identificação dos atributos mais importantes para discriminar entre as subpopulações.

Os modelos de Mistura de Dirichlet têm várias aplicações práticas, tais como a segmentação de imagens, a análise de agrupamentos de dados, a detecção de anomalias, entre outros.

Eles fornecem uma abordagem flexível para modelar dados complexos e identificar a estrutura subjacente em uma amostra, permitindo a descoberta de grupos ou subpopulações que podem ter diferentes características ou comportamentos.

Em resumo, os modelos de Mistura de Dirichlet são uma ferramenta poderosa para análise de dados e clustering, permitindo a modelagem de misturas de subpopulações não observadas e a obtenção de insights valiosos a partir dos dados.

Os Modelos de Mistura de Dirichlet são modelos estatísticos utilizados para modelar dados que podem ser representados como uma mistura de diferentes componentes ou clusters.

Eles são particularmente úteis quando os dados têm uma estrutura de clusterização latente e são aplicados em uma variedade de áreas, como análise de dados, aprendizado de máquina e reconhecimento de padrões.

Para ajustar um Modelo de Mistura de Dirichlet aos dados, você pode utilizar a biblioteca Scikit-Learn-contrib (Scikit-Learn-contrib.github.io), que é uma extensão do Scikit-Learn que inclui implementações adicionais de modelos de mistura, incluindo o Modelo de Mistura de Dirichlet.

Certifique-se de ter instalado o pacote Scikit-Learn-contrib em seu ambiente Python antes de executar o código.

Aqui está um exemplo de código atualizado usando a biblioteca Scikit-Learn-contrib:

from sklearn.mixture import BayesianGaussianMixture
import numpy as np

# Dados de exemplo
X = np.array([[1.2], [1.5], [2.3], [4.1], [4.6], [5.9]])

# Criação e ajuste do modelo de mistura de Dirichlet
model = BayesianGaussianMixture(n_components=2)
model.fit(X)

# Predição das probabilidades de pertencer a cada componente
probs = model.predict_proba(X)

# Exibição dos resultados
print("Probabilidades de pertencer a cada componente:")
for i in range(len(X)):
    print(f"Amostra {i+1}: Componente 1 = {probs[i][0]}, Componente 2 = {probs[i][1]}")

Probabilidades de pertencer a cada componente:
Amostra 1: Componente 1 = 0.9944730723532831, Componente 2 = 0.005526927646716924
Amostra 2: Componente 1 = 0.9946153996866063, Componente 2 = 0.005384600313393656
Amostra 3: Componente 1 = 0.9948757313626007, Componente 2 = 0.005124268637399353
Amostra 4: Componente 1 = 0.9949011840478539, Componente 2 = 0.00509881595214612
Amostra 5: Componente 1 = 0.9947731826235925, Componente 2 = 0.005226817376407513
Amostra 6: Componente 1 = 0.9941204089451927, Componente 2 = 0.005879591054807208

Neste exemplo, utilizamos a classe BayesianGaussianMixture do pacote sklearn.mixture para ajustar o Modelo de Mistura de Dirichlet.

O restante do código é semelhante ao exemplo anterior.

Novamente, lembre-se de ter o pacote Scikit-Learn-contrib instalado em seu ambiente Python antes de executar o código.

9.6.1.2 - Modelos de Mistura Gaussianas

Os Modelos de Mistura Gaussianas (Gaussian Mixture Models - GMMs) são uma classe popular de modelos de mistura utilizados na análise de dados e no aprendizado de máquina.

Esses modelos assumem que os dados são provenientes de uma mistura de componentes Gaussianos não observados.

Em um modelo de Mistura Gaussiana, cada componente Gaussiano representa uma subpopulação latente nos dados.

Cada subpopulação é caracterizada por uma distribuição Gaussiana com média, covariância e peso associados.

O peso indica a proporção da subpopulação na mistura total.

A inferência em um modelo de Mistura Gaussiana envolve a estimação dos parâmetros das distribuições Gaussianas de cada componente, bem como a determinação dos pesos das subpopulações.

Essa inferência geralmente é feita por meio do algoritmo Expectation-Maximization (EM), que é um método iterativo que estima os parâmetros maximizando a verossimilhança dos dados observados.

Uma vez que os parâmetros do modelo são estimados, é possível realizar várias análises e tarefas, tais como a classificação de novos dados em subpopulações, a estimativa das probabilidades de pertencimento a cada componente e a geração de dados sintéticos seguindo a distribuição aprendida.

Os Modelos de Mistura Gaussianas são amplamente utilizados em diversas aplicações, incluindo reconhecimento de padrões, segmentação de imagens, compressão de dados, detecção de anomalias e modelagem de séries temporais.

Eles são especialmente úteis quando os dados não podem ser facilmente representados por uma única distribuição Gaussiana e quando a existência de subpopulações é esperada.

Em resumo, os Modelos de Mistura Gaussianas são uma poderosa ferramenta para modelagem de dados complexos e análise de misturas de subpopulações.

Eles permitem a representação flexível de dados e a identificação de estruturas latentes nos mesmos, possibilitando uma compreensão mais profunda dos padrões presentes nos dados observados.

Aqui está um exemplo de código Python para ajustar e utilizar um modelo de Mistura Gaussiana usando a biblioteca Scikit-Learn:

from sklearn.mixture import GaussianMixture
import numpy as np

# Dados de exemplo
X = np.array([[1.2], [1.5], [2.3], [4.1], [4.6], [5.9]])

# Criação e ajuste do modelo de mistura Gaussiana
n_components = 2
model = GaussianMixture(n_components=n_components)
model.fit(X)

# Predição das probabilidades de pertencer a cada componente
probs = model.predict_proba(X)

# Exibição dos resultados
print("Probabilidades de pertencer a cada componente:")
for i in range(len(X)):
    print(f"Amostra {i+1}: Componente 1 = {probs[i][0]}, Componente 2 = {probs[i][1]}")

Probabilidades de pertencer a cada componente:
Amostra 1: Componente 1 = 1.1036681190452477e-05, Componente 2 = 0.9999889633188095
Amostra 2: Componente 1 = 4.2775300292000484e-05, Componente 2 = 0.999957224699708
Amostra 3: Componente 1 = 0.0057558473422531994, Componente 2 = 0.9942441526577467
Amostra 4: Componente 1 = 0.9999971773423728, Componente 2 = 2.822657627268628e-06
Amostra 5: Componente 1 = 0.9999999964297654, Componente 2 = 3.5702346012448835e-09
Amostra 6: Componente 1 = 1.0, Componente 2 = 3.3301345412477077e-18

Neste exemplo, utilizamos a classe GaussianMixture do pacote sklearn.mixture para ajustar um modelo de Mistura Gaussiana aos dados de exemplo X. O número de componentes do modelo é definido pela variável n_components.

Após o ajuste do modelo, utilizamos o método predict_proba para obter as probabilidades de pertencer a cada componente para cada amostra de entrada.

A saída exibe as probabilidades de pertencer a cada componente para cada amostra.

Certifique-se de ter o pacote Scikit-Learn instalado em seu ambiente Python antes de executar o código.

9.6.1.3 - Modelos de Clusterização Hierárquica

Os Modelos de Clusterização Hierárquica são uma técnica de agrupamento que visa agrupar os objetos em uma estrutura hierárquica, formando clusters aninhados uns dentro dos outros.

Esses modelos não exigem uma especificação prévia do número de clusters desejado, o que os torna flexíveis e adequados para explorar a estrutura dos dados.

Existem dois tipos principais de Modelos de Clusterização Hierárquica: Aglomerativo e Divisivo.

Aglomerativo:

O modelo aglomerativo começa com cada objeto sendo considerado um cluster separado e, em cada etapa, os clusters mais próximos são combinados até que todos os objetos estejam agrupados em um único cluster.

A medida de proximidade entre os clusters pode ser baseada na distância entre os objetos (por exemplo, distância euclidiana) ou em uma matriz de dissimilaridade pré-computada.

Os algoritmos aglomerativos mais comuns são o Single Linkage, Complete Linkage e Average Linkage.

Divisivo:

O modelo divisivo inicia com todos os objetos em um único cluster e, em cada etapa, divide o cluster em subclusters menores.

Esse processo continua até que cada objeto seja atribuído a um cluster separado.

O algoritmo divisivo mais comum é o DIANA (Divisive Analysis).

A estrutura hierárquica resultante da clusterização pode ser visualizada por meio de dendrogramas, que representam a fusão ou divisão dos clusters em diferentes níveis.

Cada nó no dendrograma representa um cluster ou a fusão/divisão de clusters.

Os Modelos de Clusterização Hierárquica têm várias vantagens, como a capacidade de identificar estruturas hierárquicas complexas nos dados, a ausência da necessidade de especificar o número de clusters de antemão e a possibilidade de visualizar a estrutura de clusterização por meio dos dendrogramas.

No entanto, eles também podem ter limitações em relação à escalabilidade e à interpretação dos resultados, especialmente em grandes conjuntos de dados.

Em resumo, os Modelos de Clusterização Hierárquica são uma técnica versátil e exploratória para agrupar objetos em uma estrutura hierárquica.

Eles permitem a identificação de padrões e estruturas nos dados sem a necessidade de especificar o número de clusters de antemão, facilitando a análise exploratória e a compreensão dos dados.

As técnicas de avaliação e seleção de modelos bayesianos são usadas para comparar e escolher o modelo mais apropriado para os dados observados.

Essas técnicas consideram tanto o ajuste do modelo aos dados quanto a complexidade do modelo em termos do número de parâmetros.

A seguir, algumas das técnicas mais comuns de avaliação e seleção de modelos bayesianos:

• Verossimilhança Marginal (Likelihood Marginal): a verossimilhança marginal, também conhecida como evidência do modelo, é uma medida que quantifica a adequação global do modelo aos dados observados. Ela é calculada integrando-se a função de verossimilhança do modelo ponderada pela distribuição a priori dos parâmetros. Modelos com maior verossimilhança marginal são preferidos, indicando um melhor ajuste aos dados.
• Informação Bayesiana do Deviance (Bayesian Deviance Information Criterion - DIC): o DIC é uma medida comumente usada para comparar modelos bayesianos. Ele leva em consideração tanto o ajuste do modelo aos dados quanto a complexidade do modelo. O DIC é calculado como o desvio médio dos dados ajustados menos a verossimilhança marginal. Quanto menor o valor do DIC, melhor o ajuste do modelo.
• Critério de Informação Bayesiana (Bayesian Information Criterion - BIC): o BIC é uma medida que penaliza a complexidade do modelo ao comparar modelos bayesianos. É calculado como o logaritmo da verossimilhança marginal menos metade do produto do número de parâmetros pelo logaritmo do tamanho da amostra. O BIC favorece modelos mais simples, penalizando aqueles com mais parâmetros.
• Amostragem Preditiva (Predictive Sampling - PS): A amostragem preditiva é usada para avaliar a capacidade do modelo de fazer previsões precisas em novos conjuntos de dados. É realizada gerando-se amostras de parâmetros do modelo a partir das cadeias de Markov Monte Carlo (MCMC) e, em seguida, gerando-se novos pontos de dados com base nessas amostras. A discrepância entre os dados observados e os dados simulados é usada para avaliar o desempenho preditivo do modelo.
• Validação Cruzada Bayesiana (Bayesian Cross-Validation - BCV): A validação cruzada bayesiana é uma técnica que divide o conjunto de dados em partes de treinamento e teste e avalia o ajuste do modelo aos dados de teste. Ela permite avaliar o desempenho do modelo em dados não observados. A validação cruzada bayesiana é computacionalmente intensiva, mas fornece uma medida mais robusta do desempenho preditivo do modelo.

Essas são apenas algumas das técnicas comumente usadas para avaliação e seleção de modelos bayesianos.

A escolha da técnica adequada depende do contexto do problema, dos dados disponíveis e dos objetivos da análise.

É importante lembrar que a avaliação e seleção de modelos bayesianos são processos iterativos e dependem da interpretação e julgamento do analista.

9.7.1.1 - Verossimilhança Marginal (Likelihood Marginal)

A Verossimilhança Marginal (Likelihood Marginal) é uma medida estatística usada para avaliar a adequação de um modelo estatístico em relação aos dados observados.

Ela é obtida integrando-se a função de verossimilhança em relação aos parâmetros do modelo.

A verossimilhança é uma medida da probabilidade de observar os dados dados os parâmetros do modelo.

Ela descreve a plausibilidade dos dados sob a hipótese do modelo.

No entanto, a verossimilhança tradicionalmente considera apenas os valores pontuais dos parâmetros.

A Verossimilhança Marginal, por outro lado, integra a verossimilhança em relação aos parâmetros do modelo, levando em consideração a incerteza sobre esses parâmetros.

Ela fornece uma medida mais abrangente da adequação do modelo aos dados, considerando todas as possíveis configurações dos parâmetros ponderadas por sua probabilidade.

A fórmula geral para a Verossimilhança Marginal é dada por:

• LMarginal = ∫ L(θ | y) * π(θ) dθ

onde:

• L(θ | y) é a função de verossimilhança condicional dos dados y dado um conjunto específico de parâmetros θ.
• π(θ) é a distribuição a priori dos parâmetros θ.

A Verossimilhança Marginal pode ser usada para comparar diferentes modelos estatísticos.

Quanto maior a Verossimilhança Marginal, melhor o ajuste do modelo aos dados.

É uma medida útil para a seleção de modelos, especialmente quando os modelos têm diferentes números de parâmetros, uma vez que penaliza automaticamente modelos mais complexos.

A Verossimilhança Marginal é frequentemente calculada usando técnicas de integração numérica, como a integração Monte Carlo ou a integração numérica determinística.

Ela desempenha um papel importante na inferência bayesiana e na escolha de modelos usando critérios bayesianos, como o Critério de Informação de Bayes (BIC) ou o Fator de Bayes (BF).

A verossimilhança marginal (likelihood marginal) é uma medida que quantifica a adequação de um modelo estatístico aos dados observados, levando em consideração a incerteza nos parâmetros do modelo.

No entanto, o cálculo direto da verossimilhança marginal geralmente é computacionalmente complexo e requer integração numérica de alta dimensionalidade.

Uma abordagem comum para estimar a verossimilhança marginal é usar técnicas de amostragem, como a amostragem de Monte Carlo (Monte Carlo sampling).

Nessa abordagem, amostras são geradas a partir da distribuição posterior dos parâmetros do modelo e, em seguida, a verossimilhança é calculada para cada amostra.

A média dessas verossimilhanças amostrais fornece uma estimativa da verossimilhança marginal.

Aqui está um exemplo de código Python que ilustra como estimar a verossimilhança marginal usando amostragem de Monte Carlo:

import numpy as np
import scipy.stats as stats

# Função que calcula a verossimilhança para um conjunto de parâmetros
def likelihood(parameters, data):
    # Implemente a função de verossimilhança específica para o seu modelo

# Função para amostragem de Monte Carlo
def monte_carlo_sampling(parameters, data, n_samples):
    # Gerar amostras da distribuição posterior dos parâmetros
    posterior_samples = np.random.multivariate_normal(parameters['mean'], parameters['cov'], size=n_samples)
    
    # Calcular a verossimilhança para cada amostra
    likelihood_samples = np.zeros(n_samples)
    for i in range(n_samples):
        likelihood_samples[i] = likelihood(posterior_samples[i], data)
    
    # Calcular a média das verossimilhanças amostrais
    marginal_likelihood = np.mean(likelihood_samples)
    
    return marginal_likelihood

# Exemplo de utilização
# Parâmetros da distribuição posterior
parameters = {
    'mean': [1.0, 2.0],  # Média dos parâmetros
    'cov': [[1.0, 0.5], [0.5, 2.0]]  # Covariância dos parâmetros
}

# Dados observados
data = np.array([1.5, 2.5, 3.5, 4.5])

# Número de amostras de Monte Carlo
n_samples = 1000

# Estimar a verossimilhança marginal
marginal_likelihood = monte_carlo_sampling(parameters, data, n_samples)

print("Verossimilhança marginal:", marginal_likelihood)

Neste exemplo, a função likelihood deve ser implementada de acordo com o modelo estatístico específico que está sendo utilizado.

Ela recebe um conjunto de parâmetros e os dados observados e retorna a verossimilhança correspondente.

A função monte_carlo_sampling realiza a amostragem de Monte Carlo a partir da distribuição posterior dos parâmetros.

Ela utiliza a função np.random.multivariate_normal para gerar amostras da distribuição posterior.

Em seguida, calcula a verossimilhança para cada amostra e retorna a média das verossimilhanças amostrais como a estimativa da verossimilhança marginal.

Você pode adaptar esse código de acordo com o seu modelo estatístico e a forma como a verossimilhança é calculada para obter uma estimativa da verossimilhança marginal.

Exemplo funcional:

import numpy as np
import scipy.stats as stats

# Função que calcula a log-verossimilhança para um conjunto de parâmetros
def likelihood(parameters, data):
    mean = parameters[0]
    std = abs(parameters[1])  # Garante que o desvio padrão seja positivo
    # Calcular a log-verossimilhança dos dados sob a distribuição normal
    return np.sum(stats.norm(mean, std).logpdf(data))

# Função para amostragem de Monte Carlo
def monte_carlo_sampling(parameters, data, n_samples):
    # Garantir que a matriz de covariância é positiva definida e simétrica
    cov_matrix = np.array(parameters['cov'])
    if np.any(np.linalg.eigvals(cov_matrix) <= 0):
        cov_matrix = np.dot(cov_matrix, cov_matrix.T)  # Torna a matriz definitivamente positiva

    # Gerar amostras da distribuição posterior dos parâmetros
    posterior_samples = np.random.multivariate_normal(parameters['mean'], cov_matrix, size=n_samples)
    
    # Calcular a log-verossimilhança para cada amostra
    likelihood_samples = np.zeros(n_samples)
    for i in range(n_samples):
        likelihood_samples[i] = likelihood(posterior_samples[i], data)
    
    # Calcular a média das log-verossimilhanças amostrais e exponenciar para obter a verossimilhança marginal
    marginal_likelihood = np.exp(np.mean(likelihood_samples))
    
    return marginal_likelihood

# Exemplo de utilização
parameters = {
    'mean': [1.0, 2.0],
    'cov': [[1.0, 0.5], [0.5, 2.0]]
}

data = np.array([1.5, 2.5, 3.5, 4.5])
n_samples = 1000
marginal_likelihood = monte_carlo_sampling(parameters, data, n_samples)

print("Verossimilhança marginal:", marginal_likelihood)

Verossimilhança marginal: 0.0

9.7.1.2 - Informação Bayesiana do Deviance (Bayesian Deviance Information Criterion - DIC)

A Informação Bayesiana do Deviance (Bayesian Deviance Information Criterion - DIC) é uma medida de ajuste de modelo usada na inferência bayesiana.

Ela foi proposta por Spiegelhalter et al. (2002) como uma alternativa ao Critério de Informação de Akaike (AIC) para modelos bayesianos.

O DIC é uma medida de qualidade do ajuste do modelo que leva em consideração tanto o ajuste aos dados quanto a complexidade do modelo.

É calculado a partir do desvio bayesiano (deviance) e da média dos desvios bayesianos ajustados (deviances ajustados) obtidos a partir de uma amostra da distribuição posterior dos parâmetros.

A fórmula geral para o DIC é dada por:

• DIC = deviance médio + pD

onde:

• deviance médio: média dos desvios bayesianos ajustados obtidos a partir da amostra da distribuição posterior dos parâmetros.
• pD: penalização do modelo, calculada como a diferença entre o deviance médio e o deviance esperado sob a distribuição posterior dos parâmetros.

O deviance é uma medida de ajuste do modelo aos dados e é calculado como a diferença entre a log-verossimilhança dos dados observados e a log-verossimilhança predita pelo modelo.

Quanto menor o deviance, melhor o ajuste do modelo aos dados.

O DIC leva em consideração a complexidade do modelo por meio da penalização pD.

Modelos mais complexos são penalizados com um valor maior de pD, o que favorece modelos mais simples.

Portanto, o DIC é uma medida que busca o equilíbrio entre o ajuste aos dados e a complexidade do modelo.

Em termos gerais, quanto menor o valor do DIC, melhor o ajuste do modelo aos dados e menor a complexidade do modelo.

Portanto, o DIC pode ser usado para comparar modelos alternativos e selecionar o modelo que tenha o menor DIC como o mais adequado aos dados.

O cálculo do DIC envolve a obtenção de uma amostra da distribuição posterior dos parâmetros usando técnicas de inferência bayesiana, como a amostragem de Monte Carlo Markov Chain (MCMC).

A partir dessa amostra, é possível calcular o deviance médio e a penalização pD para obter o valor final do DIC.

Para calcular o DIC, siga os seguintes passos:

Estime a distribuição posterior dos parâmetros do modelo usando técnicas de inferência bayesiana, como MCMC.

Isso envolve a geração de uma cadeia de amostras dos parâmetros do modelo a partir da distribuição posterior.

Para cada amostra da distribuição posterior, calcule o desvio bayesiano (deviance).

O deviance é uma medida de ajuste do modelo aos dados e pode ser calculado como a diferença entre a log-verossimilhança dos dados observados e a log-verossimilhança predita pelo modelo para cada amostra.

Calcule a média dos desvios bayesianos ajustados (deviances ajustados).

Para cada amostra da distribuição posterior, ajuste o modelo usando os parâmetros da amostra e calcule o deviance para os dados de treinamento.

Em seguida, calcule a média desses desvios ajustados para todas as amostras da distribuição posterior.

Calcule a penalização do modelo (pD) como a diferença entre o deviance médio e o deviance esperado sob a distribuição posterior dos parâmetros.

O deviance esperado é calculado substituindo os parâmetros do modelo pelos valores médios da distribuição posterior.

Calcule o DIC somando o deviance médio e a penalização do modelo.

Quanto menor o valor do DIC, melhor o ajuste do modelo aos dados.

É importante ressaltar que o cálculo do DIC depende da obtenção de uma amostra da distribuição posterior dos parâmetros, o que requer a aplicação de técnicas de inferência bayesiana adequadas.

Além disso, o DIC é mais eficaz quando usado para comparar modelos alternativos, selecionando aquele com o menor DIC como o mais adequado aos dados.

O DIC é uma medida popular na inferência bayesiana devido à sua capacidade de avaliar tanto o ajuste do modelo aos dados quanto a complexidade do modelo.

Ele fornece uma abordagem balanceada para a seleção de modelos e pode ser usado em uma variedade de contextos de modelagem bayesiana.

O critério de informação bayesiana do deviance (DIC) é uma medida usada para comparar modelos estatísticos em uma abordagem bayesiana.

Ele combina a adequação do modelo aos dados (deviance) com a complexidade do modelo, fornecendo uma métrica para selecionar o melhor modelo em termos de ajuste e parcimônia.

A fórmula geral para o DIC é a seguinte:

• DIC = deviance médio + penalização

Onde:

• Deviance médio: é a média da deviance dos valores amostrados da distribuição posterior dos parâmetros do modelo.
• Penalização: é uma medida da complexidade do modelo, calculada como a diferença entre a deviance média e a deviance do valor esperado dos parâmetros.

Aqui está um exemplo de código Python que ilustra como calcular o DIC para um modelo usando amostragem de Monte Carlo:

import numpy as np

# Função que calcula a deviance para um conjunto de parâmetros
def deviance(parameters, data):
    # Implemente a função de deviance específica para o seu modelo

# Função para amostragem de Monte Carlo
def monte_carlo_sampling(parameters, data, n_samples):
    # Gerar amostras da distribuição posterior dos parâmetros
    posterior_samples = np.random.multivariate_normal(parameters['mean'], parameters['cov'], size=n_samples)
    
    # Calcular a deviance para cada amostra
    deviance_samples = np.zeros(n_samples)
    for i in range(n_samples):
        deviance_samples[i] = deviance(posterior_samples[i], data)
    
    return deviance_samples

# Exemplo de utilização
# Parâmetros da distribuição posterior
parameters = {
    'mean': [1.0, 2.0],  # Média dos parâmetros
    'cov': [[1.0, 0.5], [0.5, 2.0]]  # Covariância dos parâmetros
}

# Dados observados
data = np.array([1.5, 2.5, 3.5, 4.5])

# Número de amostras de Monte Carlo
n_samples = 1000

# Realizar a amostragem de Monte Carlo para obter as deviances amostrais
deviance_samples = monte_carlo_sampling(parameters, data, n_samples)

# Calcular a deviance média
deviance_mean = np.mean(deviance_samples)

# Calcular a deviance do valor esperado dos parâmetros
parameters_mean = parameters['mean']  # Valor esperado dos parâmetros
deviance_expected = deviance(parameters_mean, data)

# Calcular o DIC
penalization = deviance_mean - deviance_expected
DIC = deviance_mean + penalization

print("DIC:", DIC)

Neste exemplo, a função deviance deve ser implementada de acordo com o modelo estatístico específico que está sendo utilizado.

Ela recebe um conjunto de parâmetros e os dados observados e retorna a deviance correspondente.

A função monte_carlo_sampling realiza a amostragem de Monte Carlo a partir da distribuição posterior dos parâmetros, gerando amostras usando a função np.random.multivariate_normal.

Em seguida, calcula a deviance para cada amostra.

Após obter as deviances amostrais, o código calcula a deviance média e a deviance do valor esperado dos parâmetros.

Em seguida, calcula a penalização subtraindo a deviance esperada da deviance média.

Finalmente, o DIC é calculado somando a deviance média e a penalização.

Lembrando que este é apenas um exemplo ilustrativo e a implementação exata pode variar dependendo do modelo estatístico específico que está sendo utilizado.

9.7.1.3 - Critério de Informação Bayesiana (Bayesian Information Criterion - BIC)

O Critério de Informação Bayesiana (Bayesian Information Criterion - BIC) é uma medida utilizada na seleção de modelos em inferência bayesiana.

Assim como o Critério de Informação de Akaike (AIC), o BIC busca encontrar um equilíbrio entre o ajuste do modelo aos dados e a complexidade do modelo.

O BIC é calculado usando a função de verossimilhança e o número de parâmetros do modelo.

A fórmula geral do BIC é dada por:

• BIC = -2 * log(L) + k * log(n)

Onde:

• L é a função de verossimilhança do modelo, que mede o ajuste do modelo aos dados observados.
• k é o número de parâmetros do modelo.
• n é o número de observações nos dados.

O BIC penaliza modelos mais complexos, adicionando um termo proporcional ao número de parâmetros multiplicado pelo logaritmo do número de observações.

Esse termo penaliza a inclusão de parâmetros adicionais no modelo, favorecendo modelos mais simples.

A interpretação do BIC é similar ao AIC.

Um valor menor de BIC indica um melhor ajuste do modelo aos dados.

Ao comparar modelos, o modelo com o menor valor de BIC é considerado preferível.

No entanto, é importante destacar que o BIC é mais rigoroso na penalização de modelos complexos do que o AIC, levando a uma maior ênfase na simplicidade do modelo.

É importante ressaltar que o BIC é adequado para a seleção de modelos quando se trabalha com inferência bayesiana, mas sua interpretação deve ser feita em conjunto com outras evidências e considerações específicas do contexto do problema.

Além disso, assim como o AIC, o BIC pressupõe que o modelo seja corretamente especificado e que a distribuição dos erros seja aproximadamente normal.

O Critério de Informação Bayesiana (Bayesian Information Criterion - BIC) é uma medida usada para comparar modelos estatísticos em uma abordagem bayesiana.

O BIC é uma extensão do Critério de Informação Akaike (AIC) que incorpora uma penalização adicional para a complexidade do modelo.

A fórmula geral para o BIC é a seguinte:

BIC = -2 * log_verossimilhança + k * log(n)

Onde:

log_verossimilhança: é o logaritmo da verossimilhança do modelo, ou seja, a função de verossimilhança avaliada nos parâmetros estimados.

k: é o número de parâmetros estimados no modelo.

n: é o número de observações nos dados.

O BIC busca encontrar um equilíbrio entre o ajuste do modelo aos dados e sua complexidade. Quanto menor o valor do BIC, melhor o modelo em termos de ajuste e parcimônia.

Aqui está um exemplo de código Python para calcular o BIC para um modelo:

import numpy as np

# Função que calcula a log-verossimilhança para um conjunto de parâmetros
def log_likelihood(parameters, data):
    # Implemente a função de log-verossimilhança específica para o seu modelo

# Função para calcular o BIC
def calculate_bic(log_likelihood, k, n):
    bic = -2 * log_likelihood + k * np.log(n)
    return bic

# Exemplo de utilização
# Parâmetros estimados do modelo
parameters = [1.0, 2.0, 3.0]

# Dados observados
data = [1.5, 2.5, 3.5, 4.5]

# Número de parâmetros estimados
k = len(parameters)

# Número de observações nos dados
n = len(data)

# Calcular a log-verossimilhança
log_likelihood_value = log_likelihood(parameters, data)

# Calcular o BIC
bic = calculate_bic(log_likelihood_value, k, n)

print("BIC:", bic)

Neste exemplo, a função log_likelihood deve ser implementada de acordo com o modelo estatístico específico que está sendo utilizado.

Ela recebe um conjunto de parâmetros e os dados observados e retorna a log-verossimilhança correspondente.

Em seguida, a função calculate_bic recebe a log-verossimilhança, o número de parâmetros estimados (k) e o número de observações nos dados (n) e calcula o valor do BIC usando a fórmula mencionada anteriormente.

Lembrando que este é apenas um exemplo ilustrativo e a implementação exata pode variar dependendo do modelo estatístico específico que está sendo utilizado.

9.7.1.4 - Amostragem Preditiva (Predictive Sampling - PS)

A Amostragem Preditiva (Predictive Sampling - PS) é uma abordagem usada na inferência bayesiana para gerar amostras de previsões futuras com base em um modelo estatístico ajustado aos dados observados.

A ideia por trás da PS é obter uma distribuição de probabilidade para as quantidades de interesse futuras, levando em consideração a incerteza do modelo e dos parâmetros.

A PS é útil quando estamos interessados em fazer previsões sobre eventos futuros ou quantidades desconhecidas.

Em vez de fornecer apenas um único valor de previsão, a PS fornece uma distribuição de probabilidade que representa a incerteza associada à previsão.

O processo de PS envolve várias etapas:

• Ajuste do modelo aos dados: Primeiramente, é necessário ajustar um modelo estatístico aos dados observados. Isso pode ser feito usando técnicas de inferência bayesiana, como a MCMC (Cadeia de Markov Monte Carlo) ou amostragem de Gibbs.
• Amostragem dos parâmetros: Após o ajuste do modelo, são amostrados valores dos parâmetros do modelo usando as distribuições a posteriori obtidas no passo anterior. Isso permite considerar a incerteza nos parâmetros ao fazer previsões.
• Amostragem preditiva: Com base nos valores amostrados dos parâmetros, são geradas amostras de previsões futuras. Essas amostras podem ser obtidas aplicando o modelo ajustado a novos conjuntos de dados simulados ou gerando valores preditivos diretamente do modelo.
• Sumarização das previsões: As amostras de previsões geradas são resumidas em uma distribuição de probabilidade ou estatísticas relevantes, como média, mediana, intervalos de confiança, etc. Essas informações fornecem uma visão abrangente das previsões futuras e sua incerteza associada.

A Amostragem Preditiva é uma técnica poderosa na inferência bayesiana, pois leva em consideração tanto a incerteza nos parâmetros quanto a incerteza do modelo ao fazer previsões.

Ela fornece uma abordagem flexível para lidar com a complexidade e a variabilidade inerentes aos dados e permite uma tomada de decisão mais informada e robusta.

A Amostragem Preditiva (Predictive Sampling - PS) é uma técnica usada na inferência bayesiana para realizar previsões sobre novos dados com base nos parâmetros estimados do modelo. A ideia é gerar amostras aleatórias dos parâmetros do modelo e usá-las para simular observações futuras.

Aqui está um exemplo de código Python para realizar a Amostragem Preditiva:

import numpy as np
import scipy.stats as stats

# Dados observados
data = [1.5, 2.5, 3.5, 4.5]

# Parâmetros estimados do modelo
mean = np.mean(data)
std_dev = np.std(data)

# Número de amostras a serem geradas
num_samples = 1000

# Realizar a amostragem preditiva
predicted_samples = stats.norm.rvs(loc=mean, scale=std_dev, size=num_samples)

# Exibir as amostras preditivas
print("Amostras Preditivas:")
print(predicted_samples)

Amostras Preditivas:
[ 3.95630365  3.09805428  5.04528404  1.24790803  1.58570854  0.80591237
  1.05043343  1.67385314  3.83758404  0.75891601  1.80658889  3.25631643
  3.94843455  2.26676947  1.7642871   3.5856899   2.83178304  4.19459509
  3.69785105  1.46523896  2.98974086  3.58658568  1.43809616  1.90696461
  3.39373652  2.01903497  4.50658842  3.58418955  2.05068594  2.21095765
  2.03009327  3.4457326   4.50412709  3.68410953  2.53456246  1.35599898
  2.07933828  3.13541747  2.20742311  2.09573656  3.19109082  3.24050011
  3.40832307  4.08695806  1.75364341  2.54713034  4.2064048   2.47100847
  2.64843138  2.91573962  2.33050634  1.89113032  1.29946927  3.56877201
  2.30444238  2.2797507   2.15160533  1.83956595  2.32323986  2.12785029
  0.34855625  3.28757855  1.35273477  2.31480874  3.92435754  1.19767251
  4.13613067  2.55463984  5.10840237  2.29197188  1.55215234  2.44468598
  2.3857202   3.29408873  1.71329122  3.76880544  3.51735481  4.1946576
  1.05852623  4.17611837  2.88611241  4.91757285  1.65891193  1.59777715
  4.74714559  3.21880485  2.9129323   4.00043062  2.25773971  3.81503584
  1.92698284  4.93589025  3.16308611  3.00424287  3.64818073  0.84437639
  4.85299742  4.46226039  2.6670208   1.21010536  2.79938245  2.09002323
  3.99272362  1.10123806  1.6820952   4.44609947  4.08950293  2.89995794
  3.79917901  2.94475239  1.77595728  6.69015765  2.65105494  3.87842203
  1.26175202  2.15508982  2.72989653  4.81213028  4.85854472  0.80683039
  2.07772052  1.76721891  3.54246474  2.6121552   4.07451584  3.69292503
  3.19290416  3.625258    1.96381898  1.38632618  1.76915156  2.93808959
  3.36311386  3.31243257  3.80846566  2.62271785  2.50912704  3.41915127
  2.78765796  1.91081438  2.59598391  0.93611261  3.91190402  3.00226559
  3.34605991  3.97852517  2.31075926  3.07114628  1.17906601  4.53255481
  3.59988592  1.65659605  3.62135773  3.72367342  5.01492188  4.05841543
  2.61668395  2.58567022  3.3466907   3.34384906  2.89326039  4.26138729
  3.86014235  2.1988776   3.23110537  3.63385675  4.14340727  2.77257738
  4.88766245  3.68108461  2.88824308  2.92050351  2.34625941  4.57577782
  4.26859534  3.14155595  3.98813259  1.71296529  1.50910343  3.46852794
  2.56086731  4.23568015  1.76900271  3.46136398  4.2994047   2.4637862
  3.91368331  2.9965953   2.12555451  2.99033975  3.66049825  1.6118468
  5.32246343  0.82444311  6.61276692  2.84242267  2.71987896  1.7547991
  2.71605443  2.21862435  1.47901677  3.27294695  2.06773482  2.80723513
  5.15650463  2.64058449  2.75438379  2.27485275  2.51799496  3.31897283
  2.960789    3.43178951  3.86992097  2.77506169  3.60594481  3.09433638
  4.07506376  3.44567059  3.94096101  5.19216575  4.05366237  2.72863368
  4.16847942  3.40420777  4.79056535  3.97924529  2.20851107  3.53048707
  2.57203987  2.33796583  3.80090574  1.89061424  1.81638195  2.1461432
  3.42662729  3.78123967  2.20051432  3.27514643  3.31736968  2.34821342
  2.16415593  2.9186171   1.54798787  4.21692933  3.9386279   4.78273943
  3.77396772  2.14547853  3.1836854   4.73898792  3.2743175   4.32133097
  4.1430116   4.09067328  3.51563794  3.2113972   4.0642055   2.84791589
  2.7718845   1.73447703  1.28751097  4.38388943  2.29809666  1.9653859
  3.7172352   3.25627917  2.96603997  5.40264234  2.97710748  2.81269878
  3.59442446  3.23194878  3.44122741  4.8028049   1.04068811  2.38722765
  2.47077223  3.65170455  1.71601379  1.97085339  1.20271245  1.74610183
  3.77784517  4.613844    2.20086312  2.02397525  1.03763599  1.37454827
  2.66857928  3.11344061  2.26796721  4.00926226  1.3687587   2.45201371
  2.53449089  3.63743166  3.15160169  1.86874138  2.43301666  4.60720421
  3.77165688  4.08983468  2.59749144  1.18601114  3.83865156  3.13168435
  4.81511694  4.49385048  2.86862637  4.53659507  2.37667218  2.74007924
  1.92164029  3.55291255  1.75376457  2.69703905  1.59116276  1.57656095
  5.24557443  1.34923147  5.68338494  1.86024899  4.95575515  2.30092328
  3.12794269  3.23488586  2.72312207  2.62928424  2.26122812  1.03432789
  1.89349545  2.11058346  2.93576638  3.65937145  1.5190292   1.8705349
  5.75193362  2.22617948  5.4167352   5.04441068  3.19319603  0.66469644
  2.06350138  1.35921836  2.89695796  1.56957224  3.30263681  4.62370706
  4.38356303  3.50146792  2.86875152  2.09463227  2.96339976  3.25693772
  2.50038916  3.71492169  5.67188242  4.64038755  4.09077425  4.0753387
  2.3347745   2.88457304  3.2434196   2.38058446  4.29821664  2.49769534
  0.9366992   1.23199677  3.15873043  1.77673462  1.90798143  2.83595451
  2.80157258  2.90730054  3.56645245  4.23075298  0.63632593  3.73737864
  3.53788662  3.9705226   2.64604092  1.93739748  3.76994959  1.85249555
  2.28480991  1.7604666   1.196436    3.37800215  2.56072096  2.0853429
  2.70716175  0.39706097  2.54786539  3.21728299  1.1756273   2.03255596
  4.03813988  2.68545727  1.18873449  3.10748496  3.95868507  3.14947446
  2.69499006  0.98135692  4.55471513  3.31939658  0.6761037   1.18660159
  2.37409956  3.70424337  2.79782292  2.04724888  5.00898989  2.91971802
  3.30103356  5.3247283   3.32751814  5.83755446  0.84196282  3.30344267
  3.60285583  4.72771832  1.14052453  2.16726692  2.77392831  4.5083714
  3.0481864   2.62485727  2.72475756  2.44902614  2.29550893  3.42785031
  1.22459068  2.37756204  0.33276111  6.4298284   2.52170229  2.34535849
  0.30129924  3.88930514 -0.75878231  2.51987195  0.98600529  2.36929961
  3.82294719  4.51020986  1.00557227 -0.82601434  2.62211273  2.11489715
  3.69683624  2.93300754  2.12216518  3.68680546  4.11703909  4.38392345
  3.85939045  1.68935275  2.04824351  3.44412188  3.84315546  4.87274936
  1.24762637  4.30855886  2.68831414  3.29130727  2.84779114  2.91012926
  5.16130985  4.11743787  3.38227619  3.64390018  1.75107261  3.82521314
  3.93229657  4.28882631  2.15303901  3.06015721  2.53088671  2.63042562
  1.85776832  3.6761743   1.48367225  3.41957114  3.25300453  4.73036232
  2.73525925  4.49360014  2.97243484  0.0466506   3.79608765  3.67540809
  3.00539893  2.51838369  2.54344946 -0.30401585  3.9452783   2.01955352
  2.43634049  3.53480165  2.44380597  3.20651721  1.3737252   2.88838416
  3.90388182  2.43630676  2.90659257  1.3423      2.12356202  3.72094911
  3.68982826  3.97499126  3.70809248  3.13802065  3.10342111  2.19915325
  3.27413989  2.73049778  4.06560664  5.45428034  4.32009271  2.1875142
  3.9369968   2.93947964  2.36509359 -0.66533194  1.96430504  4.79714247
  0.99200319  0.3846169   1.87999132  3.69794308  1.9148281   3.15425691
  1.48340477  2.45771949  2.32130596  4.31047708  4.76965415  2.41588504
  4.49141246  3.52772583  1.52127304  3.79886443  1.86169365  2.21429496
  2.98648582  3.29556118  3.25839631  2.32399439  1.3459589   3.25038573
  4.10518451  4.36569505  0.61770334  3.16830287  3.4174782   1.05132233
  3.89011304  3.03175917  1.78940911  2.83383676  3.79873222  2.11934904
  2.93259247  3.3964418   4.48857323  2.62814312  2.79109076  3.51436985
  3.59900407  2.89098917  3.88949283  1.70714382  3.84968725  1.08796268
  2.81269818  2.47590227  3.74422997  4.23096988  3.21589566  2.38094471
  4.78733104  3.80757135  2.86356326  2.45166899  3.40588603  2.78456132
  4.64084328  4.37314966  3.40265368  2.14970711  2.26912847  2.64101702
  3.5111578   5.42682722  3.7834518   1.91129301  2.90445421  2.68716431
  2.93037566  0.91784444  2.66863864  3.32306204  3.13092853  2.79497051
  3.08046282  2.26932047  3.71208608  2.06278082  2.42302057  4.36566163
  1.63080338  2.30117737  3.0707474   3.86841095  1.11459409  3.03508362
  5.14697455  2.24426121  2.14585529  1.93377783  3.07318341  4.03585299
  4.09290714  2.48553968  3.00368234  2.70044629  4.30570321  3.61659796
  1.88797221  1.98313869  3.40165379  4.34759034  1.8193767   3.0477112
  3.20963892  4.62628971  3.98481106  2.0638613   3.27496191  2.31107642
  1.01213656  3.7677207   2.35227517  3.35258624  1.46822948  2.8800123
  3.95064281  2.52473762  4.21267838  1.41488222  4.77579606  2.39247405
  3.04204556  2.07203605  2.14400992  3.48330746  2.24423847  3.56930296
  2.63754207  2.31295919  1.50118045  3.12941362  2.58496173  4.25925922
  4.33391344  1.38539217  4.5945207   3.23044554  2.53550404  3.97641051
  6.0034442   4.34600411  3.47199527  4.00111689  2.29593563  4.6663183
  0.85881218  3.63237927  4.59094664  3.82372324  3.8920565   3.19533346
  2.93515642  1.41577939  3.4058217   3.43802807  5.29545741  2.84826723
  3.87997122  0.01657903  3.75446255  3.50165975  4.33920414  5.46587446
  2.8727657   3.78617779  2.90997155  4.09264091  3.63531723  3.47614788
  3.15979758  3.55906633  1.7125395   3.25472355  4.81033595  3.48901399
  1.55076608  3.17552108  3.86290911  3.30862771  3.94931359  4.19400199
  2.73410448  2.04093259  3.76407883  3.94713905  3.93181225  2.69919003
  3.87054054  5.15727093  0.00706526  3.47595604  3.25693727  3.10786713
  1.53577787  3.139471    3.58093992  2.17519345  3.61061809  1.0603227
  2.79394471  3.08389627  2.59522688  3.3483912   1.21833264  2.7148388
  1.73056727  4.05511102  3.23999186  2.38409333  0.68936913  3.45764557
  3.58685088  3.63041009  3.20663077  2.34029603  2.99539608  2.47724985
  5.2591154   2.7998601   3.51864056  2.39735822  3.83018426  3.68433762
  3.5623952   0.53963937  2.33878997  2.93642114  3.60110551  4.47532906
  3.30973228  3.19474644  1.11835479  3.24226715  3.82655032  2.73470418
  0.90752581  2.89177266  2.09603663  2.33797922  0.93219138  3.10547381
  5.1736526   3.80410475  1.35118979  4.74227232  3.28727525  4.9108729
  3.22456278  3.31965962  2.54485912  3.19650157  3.97817432  3.797851
  3.34155962  2.988527    4.00067021  3.34949039  2.27625053  1.12443424
  2.52405859  1.02736202  4.39032427  2.37690241  2.32739346  1.80163185
  3.70939651  1.46759308  2.86270216  4.38733654  2.50712103  4.85463211
  1.63583515  1.70571558  3.33097844  1.41643355  2.39801193  2.75147715
  5.68233702  2.67371755  3.88735363  2.46380793  2.92696701  1.96967174
  2.06161215  2.67980467  4.61072183  3.01088088  1.19082372  1.95886833
  0.71447722  2.60821558  2.58291424  4.36859705  3.5870809   0.56060363
  3.92890255  2.08484731  2.78497108  3.61824215  3.78337234  2.40283143
  4.98393624  3.00078206  2.65682086  4.93873009  2.70868508  2.79828297
  3.64981705  2.29838046  1.18182551  2.656808    1.70093818  2.01726622
  3.88931035  3.69657313  0.72202681  2.91330533  2.62553246  2.72387648
  2.20089     4.55304785  4.08211169  3.49246128  3.12855866 -0.09172973
  3.08186164  3.85465801  4.03985824  1.12072166  3.29420456  4.64591612
  3.54294647  3.28569017  3.60292474  4.54816535  2.88761788  3.36108748
  1.86391956  3.74303085  1.74547004  3.6329819   4.08914271  0.07718075
  3.93926121  3.13929196  3.2249522   1.67991704  2.02123693  2.44467436
  4.18784064  3.67187674  3.36698997  2.90689788  1.17806636  3.26605744
  3.26521042  1.96872678  2.65847983  4.14610348  3.03310546  3.04910481
  3.38833285  3.08622116  2.70379724  3.66583876  2.13262257  2.48289777
  3.58661105  2.47966753  2.66204101  3.10950913  2.71243433  2.27499005
  4.10871872  3.57051316  3.53565315  2.62883663  3.40494184  1.73985953
  2.4968      3.96034861  3.13534345  4.40013552  2.80680781  4.22354623
  2.13586898  3.87293459  2.92574339  1.7180225   3.64123501  1.82105668
  1.0448198  -0.08336102  2.77971908  3.68008911  4.48686168  3.50572434
  2.64829473  0.90444842  1.73283616  3.08501188  4.67340297  2.76847416
  2.4407154   2.99505505  3.05384594  2.04469885  3.69190014  1.32599625
  3.29445057  4.06178568  2.73872392  2.94123287  5.98422471  0.0632025
  3.61764561  3.24722796  1.74721809  2.9484497   1.33062707  3.79625309
  4.30372366  3.89329789  0.74545166  3.42480647  1.23875347  4.12224215
  2.56773964  3.13116373  1.82436159  2.50619221  1.23229955  0.96254339
  4.69725515  2.45753976  2.68928555  2.20135103  1.37231032  2.50264921
  2.86622416  2.72522243  1.02102736  1.42391296  1.84842351  1.32123916
  2.72893595  2.5989169   1.65963699  2.71828625  2.08348632  3.10949279
  4.1262843   2.87296961  1.91415004  4.23754534  4.18201604  0.64639106
  3.69399884  4.72415148  3.24272905  1.93455758  4.15548195  2.9113489
  1.46578045  2.27323586  3.30094595  5.15763588]

Neste exemplo, os dados observados estão armazenados na variável data.

Em seguida, os parâmetros do modelo são estimados usando alguma técnica de estimação, como o método de Máxima Verossimilhança.

O número de amostras a serem geradas é especificado pela variável num_samples.

No exemplo, são geradas 1000 amostras.

A função stats.norm.rvs do módulo scipy.stats é usada para gerar as amostras preditivas.

Ela recebe os parâmetros da distribuição normal (no exemplo, a média loc e o desvio padrão scale) e o tamanho das amostras (size) e retorna as amostras aleatórias.

As amostras preditivas geradas são armazenadas na variável predicted_samples e podem ser usadas para fazer previsões sobre novos dados ou para avaliar a incerteza das estimativas do modelo.

9.7.1.5 - Validação Cruzada Bayesiana (Bayesian Cross-Validation - BCV)

A Validação Cruzada Bayesiana (Bayesian Cross-Validation - BCV) é uma técnica usada na inferência bayesiana para avaliar o desempenho de modelos estatísticos e realizar seleção de modelos.

A BCV é uma extensão da técnica de validação cruzada tradicional, adaptada para o contexto bayesiano, levando em consideração a incerteza dos parâmetros e a complexidade do modelo.

A BCV é útil quando queremos comparar diferentes modelos estatísticos ou avaliar a capacidade de generalização de um modelo ajustado aos dados observados.

Em vez de simplesmente dividir os dados em conjuntos de treinamento e teste, como na validação cruzada tradicional, a BCV utiliza uma abordagem mais sofisticada que incorpora a incerteza dos parâmetros do modelo.

O processo de BCV envolve as seguintes etapas:

Ajuste do modelo aos dados: Primeiramente, é necessário ajustar os modelos estatísticos de interesse aos dados observados.

Isso pode ser feito usando técnicas de inferência bayesiana, como a MCMC (Cadeia de Markov Monte Carlo) ou amostragem de Gibbs.

Divisão dos dados: Os dados são divididos em k partes, chamadas de "dobras" (folds), de forma aleatória ou estratificada.

Ajuste do modelo em cada fold: Em cada iteração, um dos folds é mantido como conjunto de teste e os demais folds são usados como conjunto de treinamento.

O modelo é ajustado aos dados de treinamento, levando em consideração a incerteza dos parâmetros.

Cálculo da medida de desempenho: Com base no modelo ajustado, é calculada uma medida de desempenho para o conjunto de teste.

Isso pode ser feito usando métricas como log-verossimilhança, erro de classificação, erro quadrático médio, etc.

Média das medidas de desempenho: Repetindo as etapas 3 e 4 para todas as combinações possíveis de folds, são obtidas várias medidas de desempenho.

A média dessas medidas é calculada para obter uma estimativa geral do desempenho do modelo.

A BCV leva em consideração a incerteza dos parâmetros do modelo ao ajustá-lo em cada fold, resultando em uma avaliação mais robusta do desempenho do modelo.

Além disso, a BCV pode ser usada para realizar a seleção de modelos, comparando o desempenho de diferentes modelos e escolhendo aquele que apresenta a melhor performance média.

A Validação Cruzada Bayesiana é uma técnica útil na inferência bayesiana, pois permite uma avaliação mais precisa e realista do desempenho dos modelos, considerando a incerteza inerente à modelagem estatística.

Isso ajuda a evitar a seleção de modelos superajustados e permite uma escolha mais informada do modelo adequado aos dados observados.

A validação cruzada bayesiana (Bayesian Cross-Validation - BCV) é uma técnica usada na modelagem estatística bayesiana para avaliar o desempenho de um modelo e selecionar hiperparâmetros adequados. A BCV é uma abordagem mais robusta e intuitiva em comparação com a validação cruzada tradicional.

Infelizmente, não existe um código Python único e padronizado para a validação cruzada bayesiana, pois sua implementação pode variar dependendo do modelo e das bibliotecas utilizadas. No entanto, posso fornecer um exemplo básico de como a BCV pode ser realizada usando a biblioteca PyMC3, uma popular biblioteca de modelagem bayesiana em Python.

Aqui está um exemplo de código que demonstra o processo de validação cruzada bayesiana usando a biblioteca PyMC3:

import numpy as np
import pymc3 as pm

# Dados observados
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 3, 4, 5, 6])

# Número de iterações e tamanho da amostra para cada iteração
n_iterations = 1000
n_samples = len(x)

with pm.Model() as model:
    # Priori
    alpha = pm.Normal('alpha', mu=0, sd=10)
    beta = pm.Normal('beta', mu=0, sd=10)
    sigma = pm.HalfCauchy('sigma', beta=10)
    
    # Verossimilhança
    y_obs = pm.Normal('y_obs', mu=alpha + beta * x, sd=sigma, observed=y)
    
    # Distribuição posterior
    trace = pm.sample(n_iterations)
    
    # Validação cruzada bayesiana
    ppc = pm.sample_posterior_predictive(trace, samples=n_samples)
    bcv = np.mean((ppc['y_obs'] - y)**2)
    
print("Bayesian Cross-Validation (BCV):", bcv)

AttributeError: module 'numpy' has no attribute 'bool'.
`np.bool` was a deprecated alias for the builtin `bool`. To avoid this error in existing code, use `bool` by itself. Doing this will not modify any behavior and is safe. If you specifically wanted the numpy scalar type, use `np.bool_` here.
The aliases was originally deprecated in NumPy 1.20; for more details and guidance see the original release note at:
    https://numpy.org/devdocs/release/1.20.0-notes.html#deprecations <traceback object at 0x0000018D416B7CC0>

Neste exemplo, estamos ajustando um modelo de regressão linear bayesiana simples aos dados de entrada x e y. Usamos as variáveis alpha, beta e sigma como hiperparâmetros do modelo, com distribuições priori específicas. A verossimilhança é definida como uma distribuição normal com média alpha + beta * x e desvio padrão sigma.

Em seguida, realizamos a inferência bayesiana usando a função pm.sample para amostrar da distribuição posterior. Em seguida, usamos a função pm.sample_posterior_predictive para amostrar dados preditivos da distribuição posterior. Em seguida, calculamos o BCV como a média do quadrado das diferenças entre os valores preditos (ppc['y_obs']) e os valores observados (y).

É importante ressaltar que este é apenas um exemplo básico e a implementação exata da BCV pode variar dependendo do contexto do problema e das bibliotecas utilizadas. Recomenda-se consultar a documentação da biblioteca específica que está sendo usada para obter mais detalhes e exemplos adicionais.