4 - Gráficos Estatísticos
O gráfico estatístico é uma forma de apresentação dos dados estatísticos, cujo objetivo é o de produzir, no investigador ou no público em geral, uma impressão mais rápida e viva do fenômeno em estudo, já que os gráficos falam mais rápido à compreensão que as séries.
Para tornar possível uma representação gráfica, estabelece-se uma correspondência entre os termos da série e determinada figura geométrica, de tal modo que cada elemento da série seja representado por uma figura proporcional.
A representação gráfica de um fenômeno deve obedecer a certos requisitos fundamentais, para ser realmente útil.
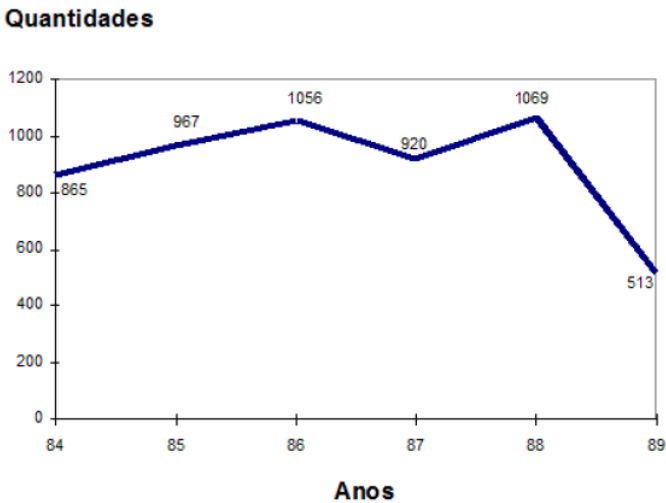
| Anos | Quantidade (mil) |
|---|---|
| 1984 | 865 |
| 1985 | 967 |
| 1986 | 1056 |
| 1987 | 920 |
| 1988 | 1069 |
| 1989 | 513 |
- Simplicidade: o gráfico deve ser destituído de detalhes de importância secundária, assim como de traços dispensáveis que possam levar o observador a uma análise demorada ou com erros.
- Clareza: o gráfico deve permitir uma correta interpretação dos valores representativos do fenômeno em estudo.
- Veracidade: o gráfico deve comunicar a verdade sobre o fenômeno em estudo.
Os gráficos constituem uma forma clara e objetiva de apresentar dados estatísticos. A intenção é a de proporcionar aos leitores em geral a compreensão e a veracidade dos fatos.
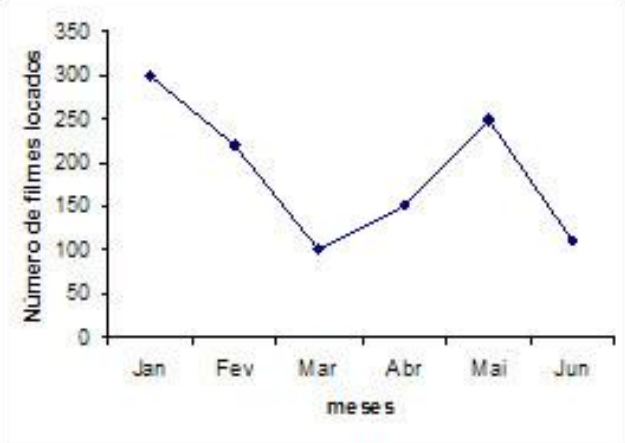
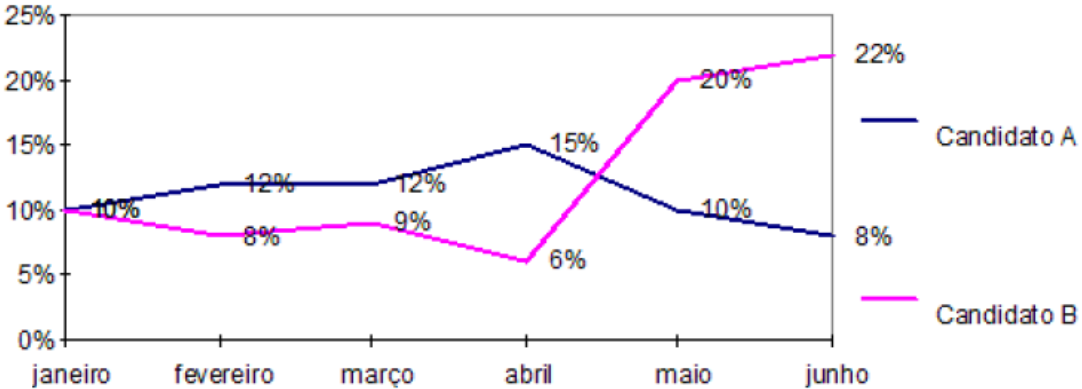
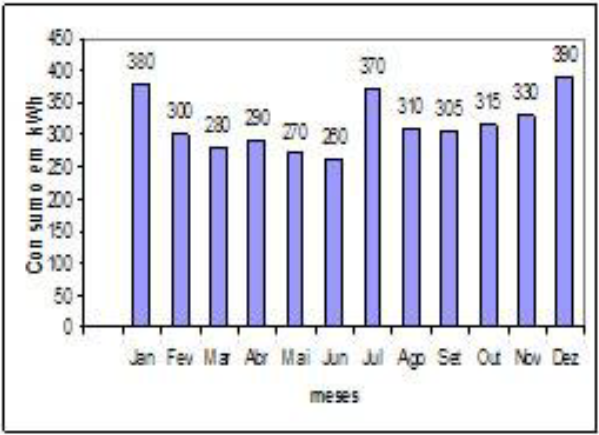
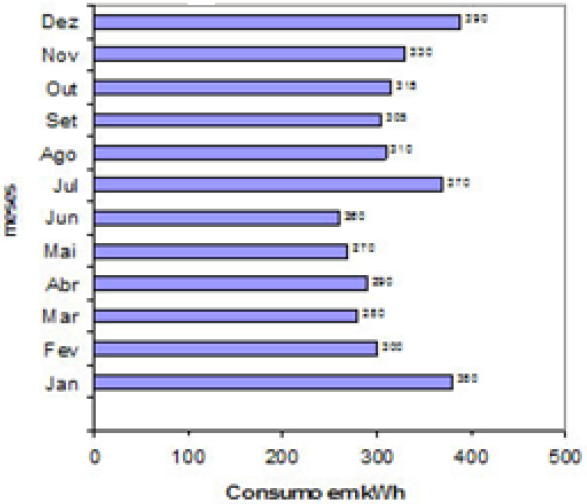
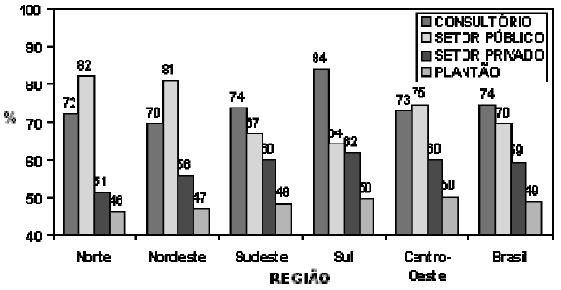
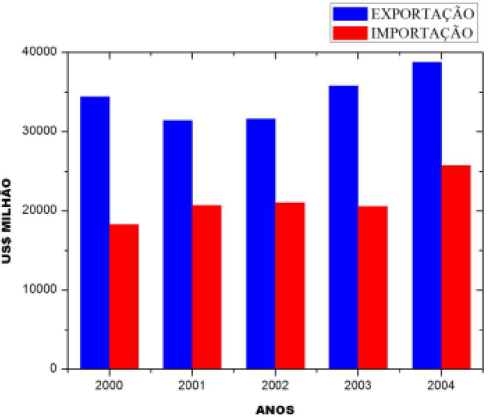
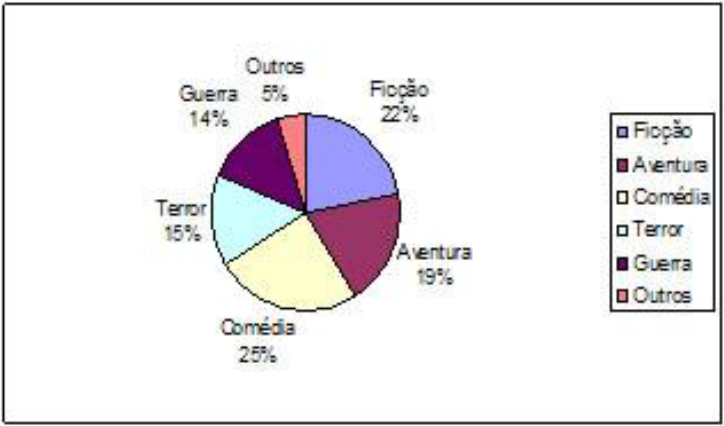
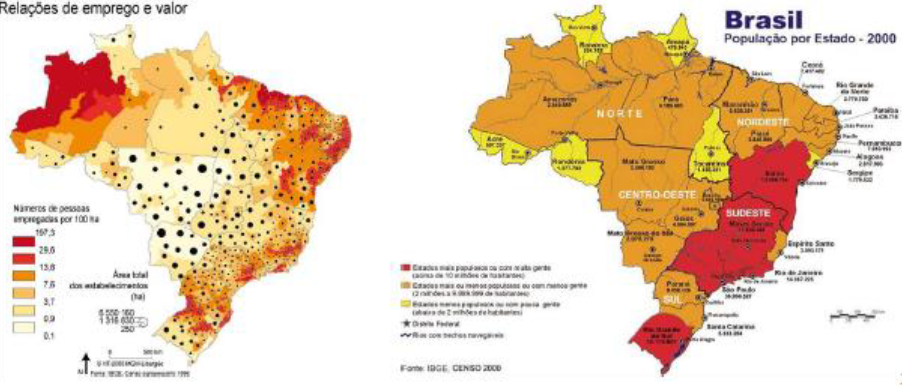
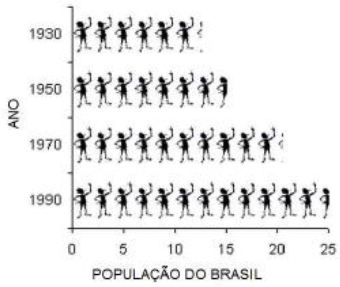
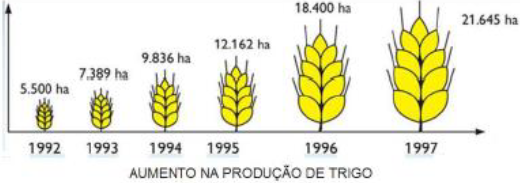
De acordo com a característica da informação precisamos escolher o gráfico correto. Os mais usuais são: gráfico de segmentos ou linhas, gráfico de barras ou colunas e gráfico de setores.
4.1 - Diagramas