6 - Medidas de Posição
O estudo feito sobre distribuições de frequência permite descrever, de maneira geral, os grupos dos valores que uma variável pode assumir.
Desse modo, pode-se localizar a maior concentração de valores de uma distribuição, isto é, se ela se localiza no início, no meio ou no final, ou, ainda, se há uma distribuição por igual.
No entanto, para ressaltar as tendências características de cada distribuição, isoladamente, ou em comparação com outras, necessita-se introduzir conceitos que se expressem através de números, que possibilitem traduzir essas tendências.
Esses conceitos denominam-se elementos típicos da distribuição e são as:
- Medidas de posição.
- Medidas de variabilidade ou dispersão.
- Medidas de assimetria.
- Medidas de curtose.
A maioria das vezes em que os dados estatísticos são analisados procura-se obter um valor para representar um conjunto de dados.
Esse valor deve sintetizar o comportamento do conjunto do qual ele é proveniente. Nem sempre os dados estudados têm um bom comportamento, isto pode fazer com que um único valor possa representá-lo ou não perante o grupo.
As medidas de posição mais relevantes são as medidas de tendência central, que recebem tal denominação porque os dados observados tendem, em geral, a se agrupar em torno dos valores centrais.
Dentre as medidas de tendência central, destacam-se as seguintes: média, moda e mediana.
Cada uma com um significado diferenciado, no entanto tendo como utilidade representar um conjunto de dados.
As outras medidas de posição são as separatrizes, que englobam: a própria mediana, os quartis e os percentis.
6.1 - Médias
6.1.1 - Média Aritmética Simples ($\bar{x}$)
É o quociente da divisão da soma dos valores de todos os dados do conjunto pela quantidade deles.
$\bar{x}$ = $\sum_{} \frac{x}{n}$ = $\sum_{i=1}^{n} \frac{x_i}{n}$ = $\frac{x_1 + x_2 + x_3 + x_4 + x_5 + ... + x_i}{n}$
Sendo $\bar{x}$ a média aritmética, $x_i$ os valores da variável e n o número de valores.
Exemplo: Média de dados não-agrupados.
Sabendo-se que as vendas diárias da empresa A, durante uma semana, foram de 10, 14, 13, 15, 16, 18 e 12 unidades. Determinar a média de vendas nesta semana feitas pela empresa A.
$\bar{x}$ = $\frac{\sum_{} x}{n}$ = $\frac{\text{10+14+13+15+16+18+12}}{7}$ = $\frac{98}{7}$ = 14
Observação:
Às vezes, a média pode ser um número diferente de todos os da série de dados que ela representa.
É o que acontece quando temos os valores 2, 4, 6 e 8, para os quais a média é 5.
Esse será o número representativo dessa série de valores, embora não esteja representado nos dados originais.
Neste caso, costuma-se dizer que a média não tem existência concreta.
6.1.2 - Média Aritmética Ponderada ($\bar{x}_p$)
É uma média aritmética na qual será atribuído um peso a cada valor da série.
$\bar{x}_p$ = $\frac{x_1 \times p_1 + x_2 \times p_2 + ... + x_n \times p_n}{p_1 + p_2 + ... + p_n}$
Exemplo:
O capital da empresa está sendo formado pelos acionistas, por financiamentos e por debêntures.
Cada tipo tem um custo diferente para a empresa, definido pela sua taxa anual.
Calcule a taxa de juros média do capital da empresa, considerando os dados apresentados na tabela seguinte.
| Capital da Empresa | Participação | Taxas de Juros |
|---|---|---|
| Acionista | R$1000,00 | 12% |
| Financiamento | R$600,00 | 8% |
| Debêntures | R$400,00 | 14% |
$\bar{x}_p$ = $\frac{{12\% \times 1000}+{8\% \times 600}+{14\% \times 400}}{1000 + 600 + 400}$ = $11\%$
6.1.3 - Média aritmética para dados agrupados sem intervalos de classes ($\bar{x}$)
As frequências são as quantidades de vezes que a variável ocorre na coleta de dados, elas funcionam como fatores de ponderação, o que leva a se calcular a média aritmética ponderada.
$\bar{x}$ = $\frac{\sum_{i=1}^{k} x_i f_i}{n}$ = $\frac{\sum_{i=1}^{k} x_i f_i }{\sum_{i=1}^{k} f_i}$ = $\frac{\sum_{} x_i f_i }{\sum_{} f_i}$
onde k é o número de intervalos de classe na tabela.
Exemplos:
1 - Após ter sido realizado um trabalho bimestral, o professor efetuou o levantamento das notas obtidas pelos alunos. Observou a seguinte distribuição e calculou a média de sua turma montando a seguinte tabela onde $x_i$ são as notas dos alunos e $f_i$ o número de alunos.
| i | $x_i$ | $f_i$ | $x_i f_i$ |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 2 | 3 | 6 |
| 3 | 3 | 5 | 15 |
| 4 | 4 | 1 | 4 |
| k = 4 | n = 10 | $\sum{} x_i f_i$ = 26 |
$\bar{x}$ = $\frac{\sum_{i=1}^{k} x_i \times f_i}{n}$ = $\frac{26}{10}$ = 2,6
2 - Consideremos a distribuição relativa a 34 famílias de quatro filhos, tomando para variável o número de filhos do sexo masculino ($x_i$ = nº meninos).
| i | $x_i$ | $f_i$ | $x_i f_i$ |
|---|---|---|---|
| 1 | 0 | 2 | 0 |
| 2 | 1 | 6 | 6 |
| 3 | 2 | 10 | 20 |
| 4 | 3 | 12 | 36 |
| 5 | 4 | 4 | 16 |
| k = 5 | $\sum_{}f_i$ = 34 | $\sum_{}x_i f_i$ = 78 |
Nesse caso, como as frequências são números indicadores da intensidade de cada valor da variável, elas funcionam como fatores de ponderação, o que nos leva a calcular a média aritmética ponderada, dada pela fórmula:
$\bar{x}$ = $\frac{\sum_{i=1}^{k} x_i \times f_i }{\sum_{i=1}^{k} f_i}$ = $\frac{\sum_{} x_i f_i }{\sum_{} f_i}$
O mais prático de obtenção da média aritmética ponderada é abrir, na tabela, uma coluna correspondente aos produtos $x_i \times f_i$.
Temos, então: $\sum_{}x_i f_i$ = 78 e $\sum_{}f_i$ = 34
Logo: $\bar{x}$ = $\frac{\sum_{} x_i \times f_i }{\sum_{} f_i}$ = $\frac{78}{34}$ = 2,3
Isto é: $\bar{x}_p$ = 2,3 meninos.
Observação: Sendo x uma variável discreta, como interpretar o resultado obtido, 2 meninos e 3 décimos de meninos? O valor médio 2,3 meninos sugere, nesse caso, que o maior número de famílias tem 2 meninos e 2 meninas, sendo porém, a tendência geral de uma leve superioridade numérica em relação ao número de meninos.
6.1.4 - Média Aritmética Para Dados Agrupados com Intervalos de Classes
Convenciona-se que todos os valores incluídos em um determinado intervalo de classe coincidem com o seu ponto médio, e determina-se a média aritmética ponderada por meio da fórmula:
$\bar{x}$ = $\frac{\sum_{i=1}^{k} x_i \times f_i}{n}$ = $\frac{\sum_{i=1}^{k} x_i \times f_i }{\sum_{i=1}^{k} f_i}$ = $\frac{\sum_{} x_i f_i }{\sum_{} f_i}$
onde k é o número de intervalos de classe na tabela e $x_i$ é o ponto médio da classe.
Exemplos:
1 - Determine a renda média familiar, de acordo com os dados da tabela abaixo:
| i | Classes: renda familiar | $x_i$ | $f_i$: Número de famílias | $x_y \times f_i$ |
|---|---|---|---|---|
| 1 | 2 |-- 4 | 3 | 5 | 15 |
| 2 | 4 |-- 6 | 5 | 10 | 50 |
| 3 | 6 |-- 8 | 7 | 14 | 98 |
| 4 | 8 |-- 10 | 9 | 8 | 72 |
| 5 | 10 |-- 12 | 11 | 3 | 33 |
| k = 5 | ∑ | | 11 | 40 | 268 |
$\bar{x}$ = $\frac{\sum_{i=1}^{k} x_i \times f_i}{n}$ = $\frac{268}{40}$ = 6,7
2 - Consideremos a distribuição:
| i | Estaturas (cm) | $f_i$ |
|---|---|---|
| 1 | 150 |-- 154 | 4 |
| 2 | 154 |-- 158 | 9 |
| 3 | 158 |-- 162 | 11 |
| 4 | 162 |-- 166 | 8 |
| 5 | 166 |-- 170 | 5 |
| 6 | 170 |-- 174 | 3 |
| ∑ = 40 |
Vamos, inicialmente, abrir uma coluna para $\bar{x}$ e outra para $xi.fi$.
| i | Estaturas (cm) | $f_i$ | $x_i$ | $x_i \times f_i$ |
|---|---|---|---|---|
| 1 | 150 |-- 154 | 4 | 152 | 608 |
| 2 | 154 |-- 158 | 9 | 156 | 1404 |
| 3 | 158 |-- 162 | 11 | 160 | 1760 |
| 4 | 162 |-- 166 | 8 | 164 | 1312 |
| 5 | 166 |-- 170 | 5 | 168 | 840 |
| 6 | 170 |-- 174 | 3 | 172 | 516 |
| k = 6 | ∑ = 40 | ∑ = 6440 |
$\bar{x}$ = $\frac{\sum_{i=1}^{k} x_i \times f_i}{\sum_{i=1}^{k} f_i}$ = $\frac{6640}{40}$ = 161
6.1.5 - Desvio em Relação à Média
Designando o desvio por $d_i$, tem–se:
$d_i = x_i - \bar{x}$
Exemplo: A produção leiteira diária da vaca A, durante uma semana, foi de 10, 14, 13, 15, 16, 18 e 12 litros.
Calcule a produção média da semana:
$\bar{x}$ = $\frac{\sum_{i=1}^{n} x}{n}$ = $\frac{10 + 14 + 13 + 15 + 16 + 18 + 12}{7}$ = $\frac{98}{7}$ = 14
onde n = 7 é o número de dados coletados.
$d_i = x_i - \bar{x}$
$d_1 = x_1 - \bar{x} = 10 - 14 = -4$
$d_2 = x_2 - \bar{x} = 14 - 14 = 0$
$d_3 = x_3 - \bar{x} = 13 - 14 = -1$
$d_4 = x_4 - \bar{x} = 15 - 14 = 1$
$d_5 = x_5 - \bar{x} = 16 - 14 = 2$
$d_6 = x_6 - \bar{x} = 18 - 14 = 4$
$d_7 = x_7 - \bar{x} = 12 - 14 = -2$
6.1.6 - Propriedades da Média
6.1.6.1 - 1ª propriedade
A soma algébrica dos desvios tomados em relação à média é nula.
$\sum_{} d_i$ = $\sum_{} (x_1 - \bar{x})$ = 0
No exemplo anterior, tem-se:
$\sum_{i=1}^{n} d_i$ = (-4) + 0 + (-1) + 1 + 2 + 4 + (-2) = (-7) + 7 = 0
Denomina-se desvio em relação à média, a diferença entre cada elemento de um conjunto de valores e a média aritmética.
6.1.6.2 - 2ª propriedade
Somando-se (ou subtraindo-se) uma constante (c) a de todos os valores de uma variável, a média do conjunto fica aumentada (ou diminuída) dessa constante.
Se $y$ = $\sum_{} {x_i \pm c}$, então $\bar{y}$ = $\bar{x} \pm c$
Somando 2 a cada um dos valores da variável do exemplo anterior, tem-se: $y_1$=12, $y_2$=16, $y_3$=15, $y_4$=17,$y_5$=18, $y_6$=20 e $y_7$=$14$.
Daí: $\sum_{i=1}^{7} y_i$ = 12 + 16 + 15 + 17 + 18 + 20 + 14 = 112
Como n = 7 e $\bar{x}$ = 14 temos: $\bar{y}$ =$\frac{112}{7}$ = 16 = 14 + 2 = $\bar{x}$ + 2
6.1.6.3 - 3ª propriedade
Multiplicando-se (ou dividindo-se) todos os valores de uma variável por uma constante (c), a média do conjunto fica multiplicada (ou dividida) por essa constante.
Se $y$ = $\sum_{i=1}^{n} {x_i \times c}$, então $\bar{y}$ = $\bar{x} \times c$
ou
Se $y$ = $\sum_{i=1}^{n} \frac{x_i}{c}$, então $\bar{y}$ = $\frac{\bar{x}}{c}$
Multiplicando por 3 cada um dos valores da variável do exemplo dado, obtém-se: $y_1$=3, $y_2$=42, $y_3$=39, $y_4$=45,$y_5$=48, $y_6$=54, $y_7$=36.
Daí, como n = 7 e $\bar{x}$ = 14 , tem-se: $\bar{y}$ = $\frac{294}{7}$ = 42 = $14 \times 3$ = $\bar{x} \times 3$
Observação: a média é utilizada quando deseja-se obter a medida de posição que possui maior estabilidade ou houver necessidade de um tratamento algébrico ulterior.
6.2 - Moda (Mo)
Dessa forma, o salário modal dos empregados de uma empresa é o salário mais comum, isto é, o salário recebido pelo maior número de empregados dessa empresa.
6.2.1 - Moda (Mo) Para Dados Não-Agrupados
Primeiramente os dados devem ser ordenados (colocados em rol) para, em seguida, se observar o valor que tem maior frequência.
Quando se trata de valores não agrupados, a moda é facilmente reconhecida: basta, de acordo com a definição, procurar o valor que mais se repete.
Denomina-se moda o valor que ocorre com maior frequência em uma série de valores.
6.2.1.1 - Conjunto Unimodal
Apresenta apenas uma moda.
x = (4, 5, 5, 6, 6, 6, 7, 7, 8, 8)
Mo = 6 (valor mais frequente)
6.2.1.2 - Conjunto Bimodal
Apresenta duas modas.
y = (1, 2, 2, 2, 3, 4, 4, 4, 5, 5, 6)
Mo = 2, Mo = 4 (valores mais frequentes)
6.2.1.3 - Conjunto Plurimodal
Apresenta várias modas.
y = (1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 6)
Mo = 2, Mo = 3, Mo = 4 (valores mais frequentes)
6.2.1.4 - Conjunto Amodal
Não apresenta valor modal, nenhum valor apareçe mais vezes que os outros.
y = (3, 5, 8, 10, 12, 13)
Observação:
- A moda é utilizada quando se deseja obter uma medida rápida e aproximada de posição ou quando a medida de posição deva ser o valor mais típico da distribuição. É uma medida pouco utilizada.
- Já a média aritmética é a medida de posição que possui maior confiabilidade numérica, além de ser mais intuitiva, do ponto de vista matemático.
6.2.2 - Moda (Mo) para Dados Agrupados sem Intervalos de Classe
Uma vez agrupados os dados, é possível determinar imediatamente a moda: basta fixar o valor da vaiável de maior frequência.
Na distribuição da tabela abaixo, à frequência máxima (12) corresponde o valor 3 da variável. Logo Mo = 3.
| Qtd | $f_i$ |
|---|---|
| 0 | 2 |
| 1 | 6 |
| 2 | 10 |
| 3 | 12 |
| 4 | 4 |
| ∑ = 34 |
6.2.3 - Moda (Mo) para Dados Agrupados com Intervalos de Classe
A classe que apresenta a maior frequência é denominada classe modal.
Pela definição, pode-se afirmar que a moda, neste caso, é o valor dominante que está compreendido entre os limites da classe modal.
O método mais simples para o cálculo da moda consiste em tomar o ponto médio da classe modal.
Esse valor denomina-se moda bruta.
Tem-se: Mo = $\frac{l^*+L^*}{2}$
Onde: l* e L* são os limites inferior e superior da classe modal.
Assim para a distribuição:
| i | estaturas (cm) | $f_i$ |
|---|---|---|
| 1 | 150 |-- 154 | 4 |
| 2 | 154 |-- 158 | 9 |
| 3 | 158 |-- 162 | 11 |
| 4 | 162 |-- 166 | 8 |
| 5 | 166 |-- 170 | 5 |
| 6 | 170 |-- 174 | 3 |
| $\sum_{} = 40$ |
temos que a classe modal é i = 3, l* = 158 e L* = 162:
Mo = $\frac{l^* + L^*}{2}$ = $\frac{158 + 162}{2}$ = $\frac{320}{2}$ = 160 cm
Observação: existem, para o cálculo da moda, outros métodos mais elaborados, como por exemplo, o que faz uso da fórmula de Czuber na qual:
$Mo = l^* + \frac{D_1}{D_1+D_2} \times h^*$
Na qual:
- l* é o limite inferior da classe modal
- h* é a amplitude da classe modal
- f* a frequência simples da classe modal
- f(ant) a frequência simples da classe anterior à classe modal
- f(post) a frequência simples da classe posterior à classe modal.
- D1 = f* – f(ant)
- D2 = f* – f(post)
Assim para a distribuição:
| i | estaturas (cm) | $f_i$ |
|---|---|---|
| 1 | 150 |-- 154 | 4 |
| 2 | 154 |-- 158 | 9 |
| 3 | 158 |-- 162 | 11 |
| 4 | 162 |-- 166 | 8 |
| 5 | 166 |-- 170 | 5 |
| 6 | 170 |-- 174 | 3 |
| $\sum_{} = 40$ |
$D_1$ = 11 – 9 = 2 e $D_2$ = 11 – 8 = 3
Mo = $l^* + \frac{D_1}{D_1+D_2} \times h^*$ = 158 + $\frac{2}{2+3} \times 4$ = 158 + $\frac{8}{5}$ = 158 + 1,6 = 159,6 cm.
6.2.4 - As expressões gráficas da moda
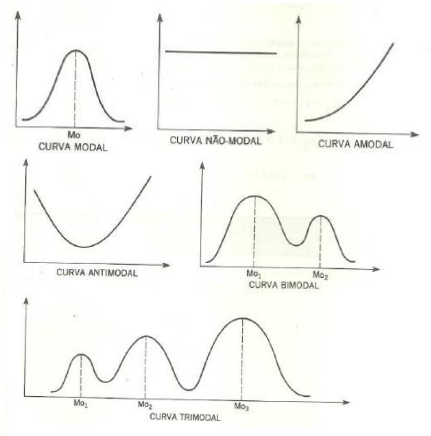 ' class='img-ext'/>
' class='img-ext'/> 6.3 - Mediana (Md)
A mediana é a medida de posição definida como o número que se encontra no centro de uma série de números, estando estes dispostos segundo uma ordem. Ou seja, a mediana de um conjunto de valores, ordenados segundo uma ordem de grandeza, é um valor situado de tal modo no conjunto que o separa em dois subconjuntos de mesmo número de elementos.
6.3.1 - Mediana (Md) para Dados Não-Agrupados
Para se descobrir o elemento mediano de uma série devem-se seguir os procedimentos abaixo:
- Se N (número de elementos do conjunto) for impar a mediana é o termo de ordem P = $\frac{N + 1}{2}$
- Se N for par, a mediana é a média aritmética dos dois termos centrais $Md_1$ e $Md_2$ de ordens $P_1$ = $\frac{N}{2}$ e $P_2$ = $\frac{N}{2} + 1$, respectivamente com Md = $\frac{Md_1+Md_2}{2}$
Exemplos:
1 - Determine o valor da mediana da série que é composta pelos seguintes elementos: 56, 65, 58, 62, e 90.
Colocar os elementos em ordem: 56, 58, 62, 65 e 90.
N = 5 (ímpar), P = $\frac{N + 1}{2} = \frac{5 + 1}{2} = 3$
Md = 62 (3º elemento)
2 - Foi realizada uma pesquisa a respeito de erros por folha cometidos por digitadores que revelou as seguintes quantidades: 12, 13, 15, 13, 12, 18, 16 e 20.
Colocar os dados em ordem no rol: 12, 12, 13, 13, 15, 16, 18 e 20.
Determinar o valor de Md com a quantidade mediana de falhas.
N = 8 (par)
$P_1$ = $\frac{N}{2}$ = $\frac{8}{2}$ = 4
$Md_1$ = 13 ($P_1$º = 4º elemento)
$P_2$ = $\frac{N}{2}$ + 1 = 4 + 1 = 5$
$Md_2$ = 15 ($P_2$º = 5º elemento)
$Md = \frac{Md_1 + Md_2}{2}$ = $\frac{13+15}{2} = \frac{28}{2} = 14$
Nota:
Ou ainda, de modo simplista, dividimos os dados em limites à esquerda e à direita, destacando os valores centrais.
Observações:
- O valor da mediana pode coincidir ou não com um elemento da série. Quando o número de elementos da série é ímpar, há coincidência. O mesmo não acontece, porém, quando esse número é par.
- Se uma lista de valores tem um número ímpar de elementos, a mediana é o valor do meio, quando a lista se apresenta ordenada; se a lista tem número par de elementos, então a mediana é a média dos dois números mais próximos do meio.
- A mediana e a média aritmética não têm, necessariamente, o mesmo valor.
Exemplo: determine a média e a mediana da série (5, 13, 10, 2, 18, 15, 6, 16, 9).
Coloque os elementos em ordem no rol: 2, 5, 6, 9, 10, 13, 15, 16, 18
Média: $\bar{x}$ = $\frac{\text{2+5+6+9+10+13+15+16+18}}{9}$ = $\frac{94}{9}$ = 10,4
Mediana: Md = 10 (5º elemento)
- A mediana depende da posição dos valores dos elementos na série ordenada.
- A mediana é designada, muitas vezes, por valor mediano.
Essa é uma das diferenças marcantes entre a mediana e a média (que se deixa influenciar, e muito, pelos valores extremos).
Exemplo:
- 5, 7, 10, 13, 15 → $\bar{x}$ = 10 e Md = 10
- 5, 7, 10, 13, 65 → $\bar{x}$ = 20 e Md = 10
A média do segundo conjunto de valores é maior do que a do primeiro, por influência dos valores extremos, ao passo que a mediana permanece a mesma.
6.3.2 - Mediana (Md) para Dados Agrupados sem Intervalos de Classe
Se os dados se agrupam em uma distribuição de frequência, o cálculo da mediana se processa de modo muito semelhante àquele dos dados não agrupados, implicando, porém, a determinação prévia das frequências acumuladas.
Precisa-se determinar um valor tal que divida a distribuição em dois grupos que contenham o mesmo número de elementos. Para o caso de uma distribuição, porém, a ordem, a partir de qualquer um dos extremos, é dada por ∑.
Neste caso, é o bastante identificar a frequência acumulada imediatamente superior à metade da soma das frequências. A mediana será o valor da variável que corresponde à tal frequência acumulada.
Exemplo:
| Qtd | $f_i$ | $F_i$ |
|---|---|---|
| 0 | 2 | 2 |
| 1 | 6 | 8 |
| 2 | 10 | 18 |
| 3 | 12 | 30 |
| 4 | 4 | 34 |
| ∑ = 34 |
Sendo $\frac{\sum_{} f_i}{2} = \frac{34}{2} = 17$, a menor frequência acumulada que supera esse valor é 18, que corresponde ao valor 2 da variável, sendo este o valor mediano.
Logo Md = 2 meninos.
Observação:
- No caso de existir uma frequência acumulada ($F_i$), tal que $F_i$ = $\frac{\sum_{} f_i}{2}$, a mediana será dada por Md = $\frac{x_i + x_i + 1}{2}$.
- A mediana será a média aritmética entre o valor da variável correspondente a essa frequência acumulada e o seguinte.
Exemplo:
| $x_i$ | $f_i$ | $F_i$ |
|---|---|---|
| 12 | 1 | 1 |
| 14 | 2 | 3 |
| 15 | 1 | 4 |
| 16 | 2 | 6 |
| 17 | 1 | 7 |
| 20 | 1 | 8 |
| ∑ = 8 |
Temos: $\frac{\sum_{} f_i}{2}$ = $\frac{8}{2}$ = $4$
Logo: $Md = \frac{x_i + x_i + 1}{2}$ = $\frac{15 + 15 + 1}{2}$ = $\frac{31}{2}$ = $15,5$
Portanto: Md = 15,5
6.3.3 - Mediana (Md) para Dados Agrupados com Intervalos de Classe
Neste caso, o problema consiste em determinar o ponto do intervalo em que está compreendida a mediana.
Para isto, temos inicialmente que determinar classe mediana, a classe na qual se acha a mediana.
Tal classe será, evidentemente, aquela correspondente à frequência acumulada imediatamente superior a $\frac{\sum_{} f_i}{2}$.
Feito isto, um problema de interpolação resolve a questão, admitindo-se, agora, que os valores se distribuam uniformemente em todo o intervalo de classe.
Assim, considerando a distribuição da tabela abaixo, acrescida das frequências acumuladas,
| i | Estaturas (cm) | $f_i$ | $F_i$ | |
|---|---|---|---|---|
| 1 | 150 |-- 154 | 4 | 4 | |
| 2 | 154 |-- 158 | 9 | 13 | |
| 3 | 158 |-- 162 | 11 | 24 | classe mediana |
| 4 | 162 |-- 166 | 8 | 32 | |
| 5 | 166 |-- 170 | 5 | 37 | |
| 6 | 170 |-- 174 | 3 | 40 | |
| ∑ = 40 |
temos: $\frac{\sum_{} f_i}{2}$ = $\frac{40}{2}$ = 20
Como há 24 valores incluídos nas três primeiras classes da distribuição e como se pretende determinar o valor que ocupa o 20º lugar, a partir do início da série, observa-se que este deve estar localizado na terceira classe (i = 3), supondo que as frequências dessas classes estejam uniformemente distribuídas.
Como existem 11 elementos nessa classe e o intervalo de classe é igual a 4, deve-se tomar, a partir do limite inferior, a distância: $\frac{20-13}{11} \times 4$ = $\frac{7}{11} \times 4$, e a mediana será dada por: Md = 158 + $\frac{7}{11} \times 4$ = 158 + $\frac{28}{11}$ = 158 + 2,54 = 160,54
Logo: Md = 160,5 cm.
Passos para o cálculo da mediana:
1º) Determinam-se as frequências acumuladas.
2º) Calcula-se $\frac{\sum_{} f_i}{2}$
3º) Marca-se a classe correspondente à frequência acumulada imediatamente superior $\frac{\sum_{} f_i}{2}$ (classe mediana). Em seguida, emprega-se a fórmula:
Md = $l^*$ + $\frac{(\frac{\sum_{} fi}{2}-F_{ant}) \times h^*}{f^*}$
na qual:
- l* é o limite inferior da classe mediana.
- Fant é a frequência acumulada da classe anterior à classe mediana.
- f* é a frequência simples da classe mediana.
- h* é a amplitude do intervalo da classe mediana.
Exemplo:
| i | Estaturas (cm) | $f_i$ | $F_i$ |
|---|---|---|---|
| 1 | 150 |-- 154 | 4 | 4 |
| 2 | 154 |-- 158 | 9 | 13 |
| 3 | 158 |-- 162 | 11 | 24 |
| 4 | 162 |-- 166 | 8 | 32 |
| 5 | 166 |-- 170 | 5 | 37 |
| 6 | 170 |-- 174 | 3 | 40 |
| ∑ = 40 |
$\frac{\sum_{} f_i}{2}$ = $\frac{40}{2}$ = 20
Logo, a classe mediana é a de ordem 3. Então: l*=158, $F_{ant}$=13, f*=11 e h*=4.
Substituindo esses valores na fórmula, obtém-se: 158 + $\frac{(20-13) \times 4}{11}$ = 158 + $\frac{26}{11}$ = 158 + 2,54 = 160,54
Isto é: Md = 160,5 cm.
Observações:
- No caso de existir uma frequência acumulada exatamente igual a ∑, a mediana será o limite superior da classe correspondente.
- Quando uma distribuição de números é razoavelmente simétrica, sem valores extremamente altos ou baixos, os valores da média e da mediana, em geral, são muito próximos um do outro.
- Há ocasiões em que a mediana constitui melhor medida de tendência central do que a média.
Exemplo:
Suponha que os valores abaixo representem vendas de pizza de muçarela por um período de 9 dias: (36, 35, 37, 29, 39, 36, 340 e 35).
Observe que, certo dia, um grande ônibus com amantes de pizza de muçarela chegou ao estabelecimento; as vendas desse tipo de pizza foram muito maiores naquele dia.
Calculando a média desses valores obtém-se: 639 / 9 = 69,22.
Entretanto, nenhum dos valores está próximo de 69,22. Ordenando inverso a relação em termos temos: (340, 39, 37, 36, 36, 36, 35, 35 e 29).
Verifica-se então que a mediana é 36.
Nesse caso, o valor da mediana dá uma ideia muito melhor do número provável das vendas em determinado dia.
Em geral, quando uma relação de valores contém um valor extremo (muito acima ou muito abaixo dos outros valores da lista), a média não é uma medida muito representativa.
6.3.4 - Emprego da mediana
Emprega-se a mediana quando:
- Deseja-se obter o ponto que divide a distribuição em partes iguais.
- Existem valores extremos que afetam de uma maneira acentuada a média.
- A variável em estudo é salário.
6.4 - Posições relativas da média, mediana e moda.
Quando uma distribuição é simétrica, as três medidas coincidem. Porém, a assimetria torna-as diferentes e essa diferença é tanto maior quanto maior é a assimetria.
Assim, em uma distribuição em forma de sino, tem-se:
- Curva simétrica: $\bar{x}$ = Md = Mo
- Curva assimétrica positiva: Mo < Md < $\bar{x}$
- Curva assimétrica negativa: $\bar{x}$ < Md < Mo

6.5 - Comparação Entre média, mediana e moda
Medida Definição Vantagens Desvantagens
Média
Centro de distribuição de frequências.
- Vantagens: Reflete cada valor. Possui propriedades matemáticas atraentes.
- Desvantagens: É afetada por valores extremos.
Mediana
Metade dos valores são maiores, metade menores.
- Vantagens: Menos sensíveis a valores extremos do que a média.
- Desvantagens: Difícil de determinar quando há uma grande quantidade de dados.
Moda
Valor mais frequente.
- Vantagens: Valor “típico”: maior quantidade de valores concentrados neste ponto.
- Desvantagens: Não se presta à análise matemática. Pode não ter moda para certos conjuntos de dados.
6.6 - Separatrizes
Outras medidas de posição, como os quartis, os decis e os percentis, embora sejam medidas de posição, possuem uma característica muito especial: separam os conjuntos em quantidades de iguais valores.
Por isso, essas medidas podem ser chamadas de separatrizes.
Alguns estudiosos de Estatística preferem chamar as separatrizes de medidas de posição e a média, a mediana e a moda (que também são medidas de posição), preferem chamar de medidas de tendência central.
Os autores não concordam quanto a melhor maneira de considerá-las.
Quartis, decis e percentis são medidas de posição, isto é, semelhantes às medidas de tendência central, indicam uma determinada localização em relação ao conjunto de dados em estudo.
Entretanto, separam o conjunto em 4 partes iguais (quartis), 10 partes iguais (decis) ou 100 partes iguais (percentis), ou seja, em partes que apresentam o mesmo número de valores.
Por isso, alguns autores preferem as medidas de posição (quartis, decis e percentis) de separatrizes (juntamente com a mediana).
6.6.1 - Quartis
Denominam-se quartis os valores de uma série que a dividem em quatro partes.
Existem, portanto, três quartis:
- Primeiro quartil ($Q_1$): valor situado de tal modo na série que uma quarta parte (25%) dos dados é menor que ele e as três quartas partes restantes (75%) são maiores.
- Segundo quartil ($Q_2$): evidentemente, coincide com a mediana ($Q_2$ = Md).
- Terceiro quartil ($Q_3$): valor situado de tal modo que as três quartas partes (75%) dos termos são menores que ele e uma quarta parte (25%) é maior.
Quando os dados são agrupados, para determinar os quartis usa-se a mesma técnica do cálculo da mediana, bastando substituir a fórmula da mediana $\frac{\sum_{} f_i}{2}$ por: $\frac{k \sum_{} f_i}{4}$, sendo k o número de ordem do quartil e $\sum_{} f_i$ a soma total das frequências simples.
Assim, tem-se:
$Q_1 = l^* + \frac{[\frac{\sum{f_i}}{4}-F_{ant}].h^*}{f^*}$
$Q_2 = l^* + \frac{[\frac{\sum{f_i}}{2}-F_{ant}].h^*}{f^*}$
$Q_3 = l^* + \frac{[\frac{3\sum{f_i}}{4}-F_{ant}].h^*}{f^*}$
Portanto
$Q_k = l^* + \frac{[\frac{k\sum{f_i}}{4}-F_{ant}].h^*}{f^*}$
Onde:
- k é o número de ordem do quartil (1, 2 ou 3)
- l* é o limite inferior da classe mediana
- Fant é a frequência acumulada da classe anterior à classe mediana
- f* é a frequência simples da classe mediana
- h* é a amplitude do intervalo da classe mediana
Exemplo: Calcular o primeiro, o segundo e o terceiro quartis da distribuição de frequência abaixo.
Estaturas dos alunos da turma A
| Estaturas (cm) | $f_i$ | $F_i$ |
|---|---|---|
| [150,154[ | 4 | 4 |
| [154,158[ | 9 | 13 |
| [158,162[ | 11 | 24 |
| [162,166[ | 8 | 32 |
| [166,170[ | 5 | 37 |
| [170,174[ | 3 | 40 |
| ∑ = 40 |
Os quartis, como já foi falado, são valores que dividem os conjuntos em 4 partes iguais.
O resultado encontrado quando se aplica a fórmula, lamentavelmente, não fornece de imediato, a posição do quartil; no entanto, indica em que linha de classe se encontra.
$\sum{f_i} = 40$
- Primeiro quartil (k = 1): $Q_1$ = $\frac{1 \times \sum{f_i}}{4} = \frac{40}{4} = 10$
- Segundo quartil (k = 2): $Q_2$ = $\frac{2 \times \sum{f_i}}{4} = \frac{80}{4} = 20$
- Terceiro quartil (k = 3): $Q_3$ = $\frac{3 \times \sum{f_i}}{4} = \frac{120}{4} = 30$
Qual é o significado, por exemplo, da posição 20 para $Q_2$?
O segundo quartil divide o conjunto em duas partes iguais.
Ainda não se sabe que valor é esse; porém o resultado 20 indica a linha (ou classe) em que se encontra.
Observação:
- Se o valor encontrado existir na linha da frequência acumulada (no nosso exercício esse valor é 20), então, esta será a classe quartil (a linha que estou procurando).
- Caso o valor não exista, a classe quartil será aquela que contiver a frequência acumulada imediatamente superior.
- No nosso caso, não existe a frequência acumulada 20, portanto a imediatamente superior é 24. Essa é a linha que estamos procurando.
Assim, como o segundo quartil se encontra na posição 20. Então, ele só pode estar na 3ª linha da Tabela de Distribuição de Frequência.
| Estaturas (cm) | $f_i$ | $F_i$ | |
|---|---|---|---|
| [150,154[ | 4 | 4 | |
| [154,158[ | 9 | 13 | $Q_1$ |
| [158,162[ | 11 | 24 | $Q_2$ |
| [162,166[ | 8 | 32 | $Q_3$ |
| [166,170[ | 5 | 37 | |
| [170,174[ | 3 | 40 | |
| ∑ = 40 |
Uma vez descobertas as classes do primeiro, segundo e terceiro quartis, pode-se destacar a linha da classe do primeiro quartil.
| Estaturas (cm) | $f_i$ | $F_i$ | |
|---|---|---|---|
| [154,158[ | 9 | 13 | $Q_1$ |
Na linha de classe de $Q_1$, as estaturas variam de 154 cm a 158 cm: o limite inferior $l^*$ (menor valor) é 154.
Na linha de classe de $Q_2$, o limite inferior da classe é 158.
Na linha de classe de $Q_3$, o limite inferior da classe é 164.
| Quartil | $\frac{k \times \sum{f_i}}{4}$ | $l^*$ | $F_{ant}$ | $h^*$ | $f^*$ | resultado |
|---|---|---|---|---|---|---|
| $Q_1$ | 10 | 154 | ||||
| $Q_2$ | 20 | 158 | ||||
| $Q_3$ | 30 | 164 |
Agora, para encontrar a frequência acumulada Fant, uma vez determinada a linha $Q_1$, basta observar a frequência acumulada da linha de cima.
Para $Q_1$, a frequência acumulada anterior será 4.
| Estaturas (cm) | $f_i$ | $F_i$ | |
|---|---|---|---|
| [150,154[ | 4 | 4 | Freq. acum. imediat. ant. |
| [154,158[ | 9 | 13 | $Q_1$ |
| Quartil | $\frac{k \times \sum{f_i}}{4}$ | $l^*$ | $F_{ant}$ | $h^*$ | $f^*$ | resultado |
|---|---|---|---|---|---|---|
| $Q_1$ | 10 | 154 | 4 | |||
| $Q_2$ | 20 | 158 | 13 | |||
| $Q_3$ | 30 | 152 | 24 |
A determinação da amplitude do intervalo de classe é imediata. Localizada a linha quartil, basta subtrair o maior valor do menor valor do intervalo de classe.
Desse modo, $Q_1$ pertence à 2ª linha e o intervalo de classe é [154,158[; a amplitude do intervalo será dada por: 158 – 154 = 4.
Efetuando o cálculo para $Q_2$ e $Q_3$ será encontrado o mesmo resultado.
| Quartil | $\frac{k \times \sum{f_i}}{4}$ | $l^*$ | $F_{ant}$ | $h^*$ | $f^*$ | resultado |
|---|---|---|---|---|---|---|
| $Q_1$ | 10 | 154 | 4 | 4 | ||
| $Q_2$ | 20 | 158 | 13 | 4 | ||
| $Q_3$ | 30 | 152 | 24 | 4 |
Consultando a tabela, identifica-se a frequência simples de cada quartil.
Assim, tem-se: 9,11 e 8, respectivamente para $Q_1$,$Q_2$ e $Q_3$.
| Quartil | $\frac{k \times \sum{f_i}}{4}$ | $l^*$ | $F_{ant}$ | $h^*$ | $f^*$ | resultado |
|---|---|---|---|---|---|---|
| $Q_1$ | 10 | 154 | 4 | 4 | 9 | |
| $Q_2$ | 20 | 158 | 13 | 4 | 11 | |
| $Q_3$ | 30 | 152 | 24 | 4 | 8 |
Solução:
$Q_1$ = $l^* + \frac{[\frac{\sum{f_i}}{4}-F_{ant}].h^*}{f^*}$ = 154 + $\frac{[10-4] \times 4}{9}$ = 156,66
$Q_2$ = $l^* + \frac{[\frac{\sum{f_i}}{2}-F_{ant}].h_2}{f^*}$ = 158 + $\frac{[20-13] \times 4}{11}$ = 160,54
$Q_3$ = $l^* + \frac{[\frac{3\sum{f_i}}{4}-F_{ant}].h_2}{f^*}$ = 162 + $\frac{[30-24] \times 4}{8}$ = 165
| Quartil | $\frac{k \times \sum{f_i}}{4}$ | $l^*$ | $F_{ant}$ | $h^*$ | $f^*$ | resultado |
|---|---|---|---|---|---|---|
| $Q_1$ | 10 | 154 | 4 | 4 | 9 | 156,66 |
| $Q_2$ | 20 | 158 | 13 | 4 | 11 | 160,54 |
| $Q_3$ | 30 | 152 | 24 | 4 | 8 | 165 |
6.6.2 - Decis
São valores que dividem o conjunto de dados ordenados (rol) em 10 (dez) partes iguais.
- Primeiro Decil ($D_l$): valor situado de tal modo na série de dados que 10% das observações são menores que ele e 90% são maiores.
- Segundo Decil ($D_2$): valor situado de tal modo na série de dados que 20% das observações são menores que ele e 80% são maiores.
- ...
- Nono Decil ($D_9$): valor situado de tal modo na série de dados que 90% das observações são menores que ele e 10% são maiores.
Para encontrarmos as posições dos decis utilizamos a fórmula $\frac{k \sum {f_i}}{10}$, sendo k o número de ordem do decil.
$D_k$ = $l^* + \frac{(\frac{k \sum_{} fi}{10} - F_{ant}) \times h^*}{f^*}$
6.6.3 - Percentis
Denominam-se percentis os 99 valores que separam uma série em 100 partes iguais.
Indicam-se: ($P_{1}$, ..., $P_{25}$, ..., $P_{50}$, ..., $P_{75}$, ..., $P_{99}$).
É evidente que $Q_2$ = $P_{50}$ = Md, $Q_1$ = $P_{25}$ e $Q_3$ = $P_{75}$.
Para encontrarmos as posições dos percentis utilizamos a fórmula $\frac{k \sum {f_i}}{100}$, sendo k o número de ordem do percentil.
$P_k$ = $l^* + \frac{(\frac{k \sum_{} fi}{100} - F_{ant}) \times h^*}{f^*}$
Exemplo: Calcular o oitavo percentil considerando a tabela de distribuição de frequência abaixo.
Altura dos alunos da turma A:
| Estaturas (cm) | $f_i$ | $F_i$ |
|---|---|---|
| [150,154[ | 4 | 4 |
| [154,158[ | 9 | 13 |
| [158,162[ | 11 | 24 |
| [162,166[ | 8 | 32 |
| [166,170[ | 5 | 37 |
| [170,174[ | 3 | 40 |
| ∑ = 40 |
Solução:
P = $l^* + \frac{(\frac{k \sum_{} fi}{100} - F_{ant}) \times h^*}{f^*}$ = $\frac{k \sum_{} fi}{100}$ = $\frac{8 \times 40}{100}$ = 3,2
Como não existe na coluna de frequência acumulada o valor 3,2; o valor imediatamente acima dele é 4.
Portanto, o percentil $P_8$ encontra-se no primeiro intervalo de classe.
$P_8$ = 150 + $\frac{(3,2 - 0) \times 4}{4}$ = 153,2
Logo, $P_8$ = 153,2 cm. Significa que 8% dos alunos possuem estatura inferior a 153,2 cm.
6.6.4 - Exemplo
Os salários (em salários mínimos) de 160 profissionais de uma empresa estão distribuídos conforme a tabela a seguir:
| faixa | $f_i$ | $F_i$ |
|---|---|---|
| 01 |-- 03 | 20 | 20 |
| 03 |-- 05 | 40 | 60 |
| 05 |-- 07 | 60 | 120 |
| 07 |-- 09 | 30 | 150 |
| 09 |-- 11 | 10 | 160 |
Calcule $Q_1$, $D_4$ e $P_85$ e interprete os resultados.
Solução:
1º passo: Determinar as frequências acumuladas da distribuição.
2º passo: Calcular a posição do Quartil, Decil ou Percentil desejado.
$Q_1$ = $\frac{1 \times 160}{4}$ = 40º elemento → Quartil
$D_4$ =$\frac{4 \times 160}{10}$ = 64º elemento → Decil
$P_{85}$ = $\frac{85 \times 160}{100}$ = 136º elemento → Percentil
3º passo: Identificar a classe que contém o quartil, o decil ou o percentil desejado por meio da frequência acumulada simples.
O segundo intervalo de classe contém o 40º valor de salário, o terceiro intervalo de classe contém o 64º valor de salário e o quarto intervalo de classe quartil contém o 136º valor de salário.
4º passo: Calcular o quartil, o decil ou o percentil desejados.
$Q_1$ = $l^* + \frac{(\frac{k \sum_{} fi}{4} - F_{ant}) \times h^*}{f^*}$ = 3 + $\frac{40-20}{40} \times 2$ = 4
$D_4$ = $l^* + \frac{(\frac{k \sum_{} fi}{10} - F_{ant}) \times h^*}{f^*}$ = 5 + $\frac{64-60}{60} \times 2$ = 5,13
$P_{85}$ = $l^* + \frac{(\frac{k \sum_{} fi}{100} - F_{ant}) \times h^*}{f^*}$ = 7 + $\frac{136-120}{30} \times 2$ = 8,07
Interpretação:
- 25% dos profissionais da empresa ganham até 4 salários mínimos ou 75% dos profissionais ganham mais de 4 salários mínimos.
- 40% dos profissionais da empresa ganham até 5,13 salários mínimos ou 60% dos profissionais ganham mais de 5,13 salários mínimos.
- 85% dos profissionais da empresa ganham até 8,07 salários mínimos ou 15% dos profissionais ganham mais de 8,07 salários mínimos.







