8 - Medidas de Assimetria e de Curtose
Nas tabelas descritivas estão presentes, além das medidas de centro e dispersão (mais utilizadas inicialmente para exploração dos dados), as informações de assimetria e curtose, chamadas medidas de forma por descreverem a forma da curva de distribuição dos dados.
8.1 - Medidas de Assimetria
As medidas de assimetria indicam o grau de assimetria de uma distribuição de frequências unimodal em relação a uma linha vertical que passa por seu ponto mais elevado.
Sendo a distribuição simétrica, a média e a moda coincidem; sendo a distribuição assimétrica à esquerda ou negativa, a média é menor que a moda; e sendo assimétrica à direita ou positiva, a média é maior que a moda.
Uma distribuição de frequências com classes é simétrica quando: Média = Mediana = Moda.
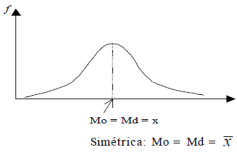
Graficamente, uma distribuição simétrica tem associada a si uma curva de frequências unimodal apresentando duas “caudas” simétricas em relação a uma linha vertical que passa por seu ponto mais alto (eixo de simetria).
Uma distribuição assimétrica tem associada a si uma curva de frequências unimodal que apresenta a partir do seu ponto mais alto, uma “cauda” mais longa para a direita (assimetria positiva) ou para a esquerda (assimetria negativa).
Nas distribuições assimétricas os valores da moda, da mediana e da média divergem sendo que a média sempre estará do mesmo lado que a cauda mais longa.
Uma distribuição de frequências com classes é assimétrica à esquerda ou negativa quando: Média < Mediana < Moda.
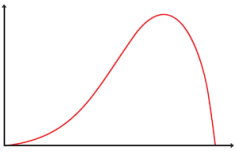
Uma distribuição de frequências com classes é assimétrica à direita ou positiva quando: Média > Mediana > Moda.
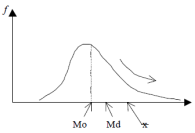
Para fazer a classificar do tipo de assimetria através de cálculo, tem-se a seguinte relação:
$\bar{x} = Mo$
Se:
- $\bar{x} - Mo = 0$: assimetria nula ou distribuição simétrica
- $\bar{x} - Mo < 0$: assimetria negativa ou à esquerda
- $\bar{x} - Mo > 0$: assimetria positiva ou à direita
8.1.1 - Coeficiente de Assimetria
8.2 - Medidas de Curtose
Denomina-se curtose o grau de achatamento de uma distribuição em relação a uma distribuição padrão, denominada curva normal (curva correspondente a uma distribuição teórica de probabilidade).
Embora seja comum explicar a curtose como o “grau de achatamento” de uma distribuição de frequências, o que as medidas de curtose buscam indicar realmente é o grau de concentração de valores da distribuição em torno do centro desta distribuição.
Numa distribuição unimodal, quanto maior for a concentração de valores em torno do centro da mesma, maior será o valor de sua curtose.
Graficamente, isso será associado a uma curva com a parte central mais afilada, mostrando um pico de frequência simples mais destacado, mais pontiagudo, caracterizando a moda da distribuição de forma mais nítida.
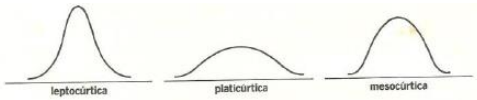
Uma distribuição de frequência pode ser classificada como:
- Mesocúrtica – quando apresenta uma medida de curtose igual à da distribuição normal.
- Platicúrtica – quando apresenta uma medida de curtose menor que a da distribuição normal.
- Leptocúrtica – quando apresenta uma medida de curtose maior que a da distribuição normal.
8.2.1 - Coeficiente de Curtose
