Estatística Básica
Carregando, aguarde alguns segundos.

5 - Distribuição de Frequência

A Distribuição de Frequência reúne o conjunto de dados em uma tabela conforme as frequências ou repartições de seus valores, podendo ser discreta ou contínua.

A Distribuição de Frequência é uma série estatística em que permanecem constantes o fato, o local e a época em que o fenômeno ocorreu.

Exemplos:

a) Distribuição de Frequência Intervalar (Contínua)

Altura em centimetros de 160 alunos:

Altura (cm) $X_i$ $f_i$
150 |-- 158 153,5 18
158 |-- 166 161,5 25
166 |-- 174 169,5 20
174 |-- 182 177,5 52
182 |-- 190 185,5 30
190 |-- 198 193,5 15
∑ = 160

b) Distribuição de Frequência Pontual (Discreta)

Moradores nas residências de 15 famílias:

$X_i$ $f_i$
1 2
2 3
3 2
4 5
5 3
∑ = 15

Resumindo as distribuições de frequência:

  • São as tabelas mais importantes para a estatística descritiva.
  • Os dados são organizados numa tabela resumida em grupos de classe ou categorias convenientemente estabelecidas e numericamente ordenadas.
  • Constitui-se num tipo de apresentação que condensa uma coleção de dados conforme as frequências ou repetições de seus valores.
  • São séries heterógrafas, isto é, séries na qual o fenômeno ou fato apresenta graduações ou subdivisões. Embora fixo o fenômeno varia de intensidade.
  • A sua construção depende do tipo dos dados: contínuos ou discretos.

5.1 - Tabela Primitiva e Rol

Geralmente dados numéricos são coletados desorganizadamente, sem uma ordenação específica, sendo denominados dados brutos.

Não estarão em ordem crescente nem em ordem decrescente.

A Tabela Primitiva apresenta estes dados brutos sequencialmente em linhas e colunas.

Exemplo: amostra com valores das estaturas de quarenta alunos do Colégio A.

Montamos uma tabela primitiva relacionando estes valores na ordem em que foram coletados:

166 160 161 150 162 160 165 167 164 160

162 161 168 163 156 173 160 155 164 168

155 152 163 160 155 155 169 151 170 164

154 161 156 172 153 157 156 158 158 161

Partindo desses dados brutos, é difícil averiguar em torno de que valor tendem a se concentrar as estaturas, qual a menor ou qual a maior estatura ou, ainda, quantos alunos se acham abaixo ou acima de uma dada estatura.

A maneira mais simples de organizar os dados é através da ordenação crescente ou decrescente dos valores.

A tabela obtida após a ordenação dos dados recebe o nome de Rol.

Montamos uma tabela relacionando os valores do rol em ordem crescente:

150 151 152 153 154 155 155 155 155 156

156 156 157 158 158 160 160 160 160 160

161 161 161 161 162 162 163 163 164 164

164 165 166 167 168 168 169 170 172 173

5.2 - Distribuição de Frequência

No exemplo trabalhado, a variável estatura será observada e estudada mais facilmente quando os valores estiverem ordenados em uma coluna e sendos colocados, ao lado de cada valor, o número de vezes que aparece repetido.

Denomina-se frequência o número de alunos que fica relacionado a um determinado valor da variável.

A tabela, assim obtida, recebe o nome de distribuição de frequência.

150 1 158 2 167 1
151 1 160 5 168 2
152 1 161 4 169 1
153 1 162 2 170 1
154 1 163 2 172 1
155 4 164 3 173 1
156 3 165 1
157 1 166 1

No entanto, o processo apresentado é ainda inconveniente, exigindo muito espaço, mesmo quando o número de valores da variável é de tamanho razoável.

Sendo possível, a solução mais aceitável, pela própria natureza da variável contínua, é o agrupamento dos valores em vários intervalos.

Quando os valores da variável estão sendo agrupados em intervalos, sendo que, em Estatística prefere-se denominar os intervalos de classes.

Chamando de frequência de uma classe o número de valores da variável pertencente à classe, os dados podem ser dispostos como na tabela a seguir denominada distribuição de frequência com intervalo de classe.

Estaturas de 40 alunos do Colégio A:

Estaturas (cm) Frequência
150 |-- 154 4
154 |-- 158 9
158 |-- 162 11
162 |-- 166 8
166 |-- 170 5
170 |-- 174 3
Total 40

Ao se agrupar os valores da variável em classes, ganha-se em simplicidade, mas perde-se em pormenores.

O que se pretende com a construção desta nova é realçar o que há de essencial nos dados e, também, tornar possível o uso de técnicas analíticas para sua total descrição, até porque a Estatística tem por finalidade específica analisar o conjunto de valores, desinteressando-se por casos isolados.

Observações:

  • Como o objetivo, desde o início, é a obtenção de uma distribuição de frequência com intervalo de classe, torna-se necessário fazer uma tabulação, com cada traço correspondendo a um valor.
  • Quando os dados estão organizados em uma distribuição de frequência, são usualmente denominados dados agrupados.

Estaturas (cm) Dados agrupados Frequência
150 |-- 154 |||| 4
154 |-- 158 ||||| ||||| 9
158 |-- 162 ||||| ||||| | 11
162 |-- 166 ||||| ||| 8
166 |-- 170 ||||| 5
170 |-- 174 ||| 3
Total 40

5.3 - Elementos de uma Distribuição de Frequência

5.3.1 - Classes de Frequência

As Classes de Frequência, ou simplesmente Classes, são intervalos de variação da variável.

As classes são representadas simbolicamente por i, sendo i = 1,2,3,...,k (onde k é de o número total de classes da distribuição).

O número total de valores da variável é simbolizado por n.

5.3.2 - Limites de Classe

O menor número é o limite inferior da classe ($l_i$) e o maior número, o limite superior da classe ($L_i$). Na segunda classe, por exemplo, tem-se: $l_2$ = 154 e $L_2$ = 158.

Classe de frequência ou, simplesmente, classes são intervalos de variação da variável.

Denominam-se limites de classe os extremos de cada classe.

O limite inferior do rol é simbolizado pela letra l e o limite superior pela letra L.

O limite inferior da classe i é simbolizado por $l_i$ e o limite superior por $L_i$, em que i é o índice da classe.

Observação:

De acordo com o IBGE as classes devem ser escritas como desta quantidade até menor que aquela, usando para isso o símbolo |--.

Assim, $l_i$ |-- $L_i$ significa inclusão de $l_i$ e exclusão de $L_i$.

O indivíduo com estatura 158 cm estaria na terceira classe (i = 3) e não na segunda.

5.3.3 - Amplitude de um Intervalo de Classe

Amplitude de um intervalo de classe, ou simplesmente intervalo de classe, é a medida do intervalo que define a classe.

O intervalo de classe i é simbolizado por $h_i$ e é obtido pela diferença entre seus limites: $h_i = L_i – l_i$

No exemplo empregado, o tamanho do intervalo da segunda classe ($h_2$) vale:

$h_2$ = $L_2$ – $l_2$ = $158 – 154$ → $h_2$ = $4 cm$.

Todas as outras classes do exemplo também têm intervalo de 4 cm, pois esse é o intervalo entre cada um dos limites inferiores e os limites superiores correspondentes.

5.3.4 - Amplitude Total da Distribuição

Amplitude total da distribuição (AT) é a diferença entre o limite superior da última classe (limite superior máximo) e o limite inferior da primeira classe (limite inferior mínimo): AT = $L_{max}$ – $l_{min}$

No exemplo utilizado, tem-se: AT = 174 – 150 → AT = 24 cm.

Observação:

É evidente que, se as classes possuem o mesmo intervalo, verificamos a relação:

$\frac{AT}{h_i}$ = k → $\frac{24}{4}$ = 6

5.3.5 - Amplitude Amostral

Amplitude amostral (AA) é a diferença entre o valor máximo e o valor mínimo da amostra: AA = $x_{max}$ – $x_{min}$

No exemplo utilizado, tem-se: AA = 173 – 150 = 23 → AA = 23 cm.

5.3.6 - Ponto Médio de uma Classe

Ponto médio de uma classe ($x_i$) é, como o próprio nome indica, o ponto que divide o intervalo de classe em duas partes iguais.

Para se obter o ponto médio de uma classe, calcula-se a semissoma dos limites da classe (média aritmética).

$x_i$ = $\frac{l_i+L_i}{2}$

Assim, o ponto médio da segunda classe, no exemplo citado anteriormente, é

$x_2$ = $\frac{l_2+L_2}{2}$ = $\frac{154 + 158}{2}$ = 156

Observação: O ponto médio de uma classe é o valor que a representa.

5.3.7 - Frequência Simples ou Absoluta

Frequência simples, (frequência absoluta, frequência de uma classe, frequência de um valor individual) é o número de observações correspondentes a essa classe ou a esse valor.

A frequência simples é simbolizada por fi (lê-se: f índice i ou frequência da classe i). Assim, no exemplo utilizado anteriormente, tem-se:

$f_1$ = 4, $f_2$ = 9, $f_3$ = 11, $f_4$ = 8, $f_5$ = 5 e $f_6$ = 3.

A soma de todas as frequências é representada pelo símbolo de somatório.

$\sum_{i=1}^{k} f_i$

É evidente que:

$\sum_{i=1}^{k}f_i = n$

Para a distribuição em estudo, tem-se:

$\sum_{i=1}^{6}f_i = 40$

Não havendo possibilidade de engano, usa-se:

$\sum_{}f_i = 40$

Pode-se, agora, dar à distribuição de frequência das estaturas dos quarenta alunos do colégio A, a seguinte representação tabular técnica.

i Estaturas (cm) $f_i$
1 150 |-- 154 4
2 154 |-- 158 9
3 158 |-- 162 11
4 162 |-- 166 8
5 166 |-- 170 5
6 170 |-- 174 3
Total ∑ = 40

5.4 - Número de Classes. Intervalos de Classe.

A primeira preocupação que se tem, na construção de uma distribuição de frequência, é a determinação do número de classes e, consequentemente, da amplitude e dos limites dos intervalos de classe.

Para a determinação do número de classes de uma distribuição pode-se lançar mão da Regra de Sturges, que permite calcular o número de classes em função da variável: $i \approx 1 + \text{3,3 log n}$, sabendo que i é o número de classe e n é o número total de dados.

Essa regra possibilitou a obtenção da tabela abaixo.

n i
3 |--| 5 3
6 |--| 11 4
12 |--| 22 5
23 |--| 46 6
47 |--| 90 7
91 |--| 181 8
182 |--| 363 9
... ...

Além da Regra de Sturges, existem outras fórmulas empíricas que pretendem resolver o problema da determinação do número de classes que deve ter a distribuição.

No entanto, a verdade é que essas fórmulas não levam a uma decisão final; esta vai depender de um julgamento pessoal, que deve estar ligado à natureza dos dados, da unidade empregada para expressá-los etc.

Decidido o número de classes que deve ter a distribuição, compete agora resolver o problema da determinação da amplitude do intervalo de classe, o que se consegue dividindo a amplitude pelo número de classes: $h = \frac{AT}{i}$

Quando o resultado não é exato, deve-se arredondá-lo para mais.

Outro problema que surge é a escolha dos limites dos intervalos, os quais deverão ser tais que forneçam, na medida do possível, para os pontos médios, números que facilitem os cálculos – números naturais.

No exemplo utilizado, tem-se: para n = 40 → i = 6.

Logo: h = $\frac{173-50}{6}$ = $\frac{23}{6}$ = 3,8 = 4, isto é, seis classes de intervalos iguais a 4.

5.5 - Tipos de frequências

Frequências simples ou absolutas ($f_i$) são os valores que realmente representam o número de dados de cada classe.

$\sum_{}f_i = n$

Frequências relativas ($f_r$) são os valores das razões entre as frequências simples e a frequência total.

$fr_i = \frac{f_i}{\sum_{}f_i}$

Logo, no exemplo utilizado, a frequência da terceira classe é:

$fr_3 = \frac{f_3}{\sum_{}f_3} = \frac{11}{40} = 0,275$

Evidentemente:

$fr_i = 1 \text{ ou } 100\%$

Observação: O propósito das frequências relativas é o de permitir a análise ou facilitar as comparações.

Frequência acumulada (Fi) é o total das frequências de todos os valores inferiores ao limite superior do intervalo de uma dada classe.

$F_k = f_1 + f_2 + f_3 + ... + f_k$

ou

$F_k = \sum{}f_i (i = 1,2,3,...,k)$

Assim, no exemplo apresentado, anteriormente, a frequência acumulada correspondente à terceira classe é:

$F_k$ = $\sum{}f_i$ = $f_1 + f_2 + f_3$ = $4 + 9 + 11$ = 24, o que significa existirem 24 alunos com estatura inferior a 162 cm (limite superior do intervalo da terceira classe).

Frequência acumulada relativa (Fri) de uma classe é a frequência acumulada da classe, dividida pela frequência total da distribuição.

$fr_i = \frac{f_i}{\sum_{}f_i}$

Assim, para a terceira classe, temos:

$fr_3$ = $\frac{f_3}{\sum_{}f_i}$ = $\frac{24}{40}$ = 0,6

Resumindo : Tabela com as frequências estudadas

i Estaturas (cm) $f_i$ $x_i$ $fr_i$ $F_i$ $Fr_i$
1 150 |-- 154 4 152 0,100 4 0,100
2 154 |-- 158 9 156 0,225 13 0,325
3 158 |-- 162 11 160 0,275 24 0,600
4 162 |-- 166 8 164 0,200 32 0,800
5 166 |-- 170 5 168 0,125 37 0,925
6 170 |-- 174 3 172 0,075 40 1,000
Total ∑ = 40 ∑ = 1

Observação:

O conhecimento dos vários tipos de frequência ajuda para que se possa responder a muitas questões com relativa facilidade, como as seguintes:

a) Quantos alunos tem estatura entre 154 cm, inclusive, e 158 cm?

Esses são os valores da variável que formam a segunda classe. Como f2 = 9, a resposta é 9 alunos.

b) Qual é a porcentagem de alunos cujas estaturas são inferiores a 154 cm?

Esses valores são os que formam a primeira classe. Como fri = 0,100, obtém – se a resposta multiplicando a frequência relativa por 100: 0,100 x 100 = 10. Logo, a porcentagem de alunos é 10%.

c) Quantos alunos têm estatura abaixo de 162 cm?

É evidente que as estaturas consideradas são aquelas que formam as classes de ordem 1, 2 e 3. Assim, o número de alunos é dado por:

$f_1 + f_2 + f_3$ = $\sum_{i=1}^{3}f_i$ = $F_3$ = 24

Portanto, 24 alunos têm estatura abaixo de 162 cm.

d) Quantos alunos têm estatura não-inferior a 158 cm? O número é dado por:

$\sum_{i=3}^{6}f_i$ = $f_3 + f_4 + f_5 + f_6$ = 11 + 8 + 5 + 3 = 27

Ou então:

$\sum_{i=1}^{6}f_i - F_2$ = $n - F_2$ = 40 - 13 = 27

5.6 - Distribuição de Frequência sem Intervalos de Classe

Quando se trata de variável discreta de variação relativamente pequena, cada valor pode ser tomado como um intervalo de classe (intervalo degenerado) e, nesse caso, a distribuição é chamada distribuição sem intervalos de classe, tomando a seguinte forma:

$x_i$ $f_i$
$x_1$ $f_1$
$x_2$ $f_2$
... ...
$x_n$ $f_n$
$\sum{}f_i=n$

Exemplo: seja X a variável “número de cômodos das casas ocupadas por vinte famílias entrevistadas”.

i $x_i$ $f_i$
1 2 4
2 3 7
3 4 5
4 5 2
5 6 1
6 7 1
∑ = 20

Completada com os vários tipos de frequência, tem-se:

i $x_i$ $f_i$ $fr_i$
1 2 4 0,20 14 0,20
2 3 7 0,35 11 0,55
3 4 5 0,25 16 0,80
4 5 2 0,10 18 0,90
5 6 1 0,05 19 0,95
6 7 1 0,05 20 1,00
∑ = 20 ∑ = 1

5.7 - Representação gráfica de uma Distribuição

Uma distribuição de frequência pode ser representada graficamente pelo histograma, pelo polígono de frequência e pelo polígono de frequência acumulada (Ogiva de Galton).

Qualquer um dos gráficos mencionados pode ser construído utilizando o primeiro quadrante do sistema de eixos coordenados cartesianos ortogonais.

Na linha horizontal (eixo das abscissas) colocam-se os valores da variável; e na linha vertical (eixo das ordenadas), as frequências.

5.7.1 - Histograma

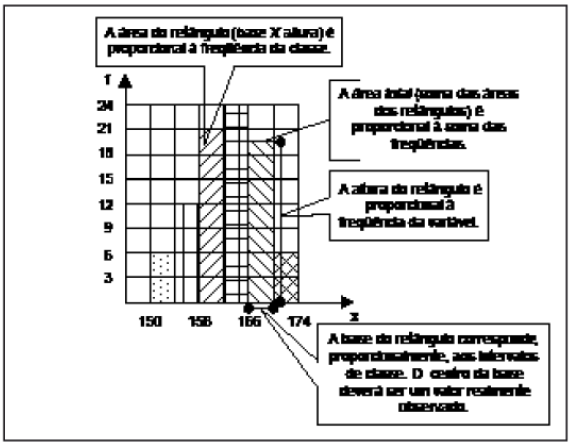
O histograma é formado por um conjunto de retângulos justapostos, cujas bases se localizam sobre o eixo horizontal, de tal modo que seus pontos médios coincidam com os pontos médios dos intervalos de classe.

Observações:

  • As larguras dos retângulos são iguais às amplitudes dos intervalos de classe.
  • As alturas dos retângulos devem ser proporcionais às frequências das classes, sendo a amplitude dos intervalos igual. Isso permite que se tomem as alturas numericamente iguais às frequências.
  • O histograma goza da seguinte propriedade: á área de um histograma é proporcional à soma das frequências.
  • Quando se usam as frequências relativas obtém-se um gráfico de área unitária.
  • Quando se pretende comparar duas distribuições, o ideal é fazê-lo pelo histograma de frequências relativas.

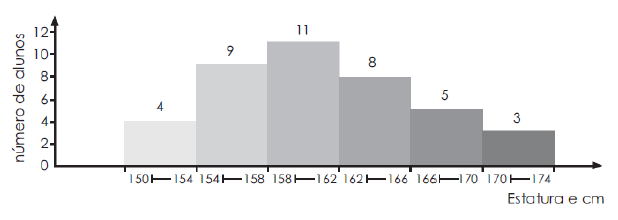
5.7.2 - Polígono de Frequência

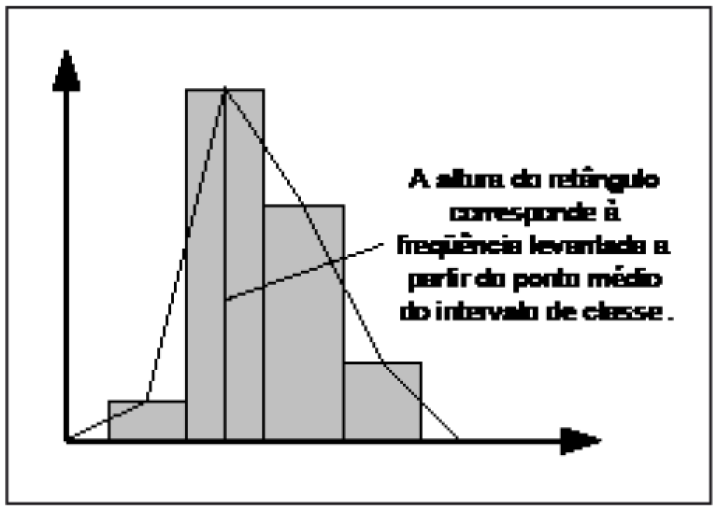
O polígono de frequência é um gráfico em linha, sendo as frequências marcadas sobre perpendiculares ao eixo horizontal, levantadas pelos pontos médios dos intervalos de classe.

Observação: Para realmente se obter um polígono (linha fechada), deve-se completar a figura, ligando os extremos da linha obtida aos pontos médios da classe anterior à primeira e da posterior à última, da distribuição.

Exemplos:

1) Construir o histograma associado à tabela abaixo, que representa as alturas (em cm) dos alunos da turma A, do Colégio Progresso, em 2018.

Estaturas (cm) Alunos ($F_i$)
150 |-- 155 4
155 |-- 160 8
160 |-- 165 15
165 |-- 170 10
170 |-- 175 8
∑=45

Resposta: Histograma de Frequências Simples

2) Seguir e observar como ficam os histogramas para as frequências simples e acumuladas crescentes, referentes às médias dos alunos da turma A, do Colégio União, em julho de 2018.

Notas Freq. Simples ($F_i$) Freq. Acum. Cr.
0 |-- 2 3 3
2 |-- 4 5 8
4 |-- 6 10 18
6 |-- 8 6 24
8 |-- 10 2 26
∑=26

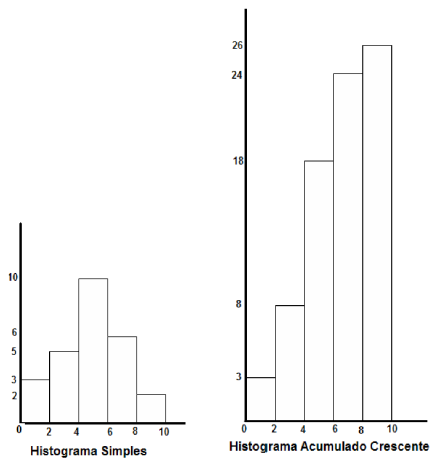
3) Observar o polígono de frequência que representa o exemplo anterior.

5.7.3 - Polígono de Frequência Acumulada

O polígono de frequência acumulada é traçado marcando-se as frequências acumuladas sobre perpendiculares ao eixo horizontal, levantadas nos pontos correspondentes aos limites superiores dos intervalos de classe.

Exemplo: exercício completo.

Análise do desempenho dos alunos do Professor Paulo.

1ª etapa: Levantamento dos dados brutos (Tabela primitiva)

5 7 7 2 0 0 3 9 8 4 8 4 1 7 9 6 7 7 1 4 0 2 1 1

3 9 7 5 6 4 9 8 6 5 4 0 8 9 3 2 9 6 8 7 4 5 4 8

3 2 8 8 0 5 3 5 1 5 9 0 9 9 3 9 8 8 7 5 8 7 0 2

7 7 1 7 7 1 7 0 6 3 2 0 2 7 8 6 2 1 6 7 4 6 9 6

5 1 7 9 2 5 9 1 8 5 2 8 7 3 0 7 8 8 6 9 7 4 8 3

5 2 5 1 8 8 8 7 4 0 3 6 2 9 8 4 8 5 8 6 5 8 6 4

2 1 1 0 3 9 0 3 8 1 2 9 1 7 4 9 0 3 8 1 2 9 7 7

2ª etapa: Construção de rol

0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1

1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 3 3

3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 4 4 4 5

5 5 5 5 5 5 5 5 5 5 5 5 5 5 6 6 6 6 6 6 6 6 6 6

6 6 6 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7

7 7 7 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8

8 8 8 8 8 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9

3ª etapa: Construção da tabela de frequência

Notas Frequência
0 14
1 16
2 15
3 13
4 13
5 15
6 13
7 24
8 26
9 19
10 0
∑=168

4ª etapa: Construção da tabela de frequência com intervalos de classe

$\text{amplitude-total}$ = $\text{nota-maior}$ - $\text{nota-menor}$ = 9 - 0 = 9

$\text{intervalo-classes}$ = $\frac{\text{amplitude-total}}{\text{numero-classes}}$ = $\frac{9}{5}$ = 1,8 = 2

5ª etapa: Representação gráfica (polígono de frequência)

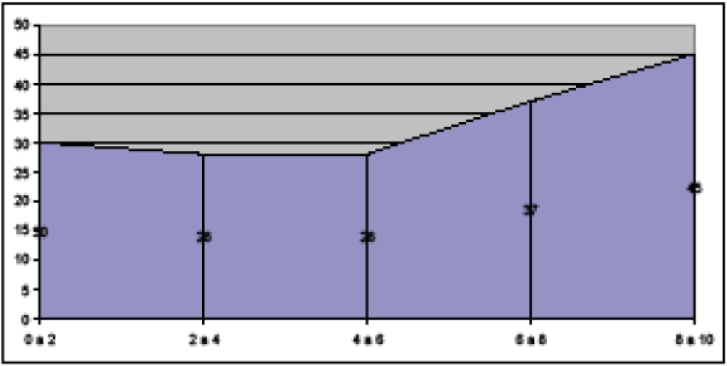
Observação: Concluindo o estudo, o polígono de frequência parece demonstrar que o resultado do trabalho do professor Paulo é satisfatório, pois há mais alunos acima do intervalo 4 a 6 do que abaixo dele.

5.8 - Curva de Frequência (Curva Polida)

A tendência da análise de populações cada vez mais amplas é de que a linha poligonal se torne uma curva. Essa curva recebe a denominação de curva de frequência.

Enquanto o polígono de frequência apresenta a imagem real do fenômeno estudado, a curva de frequência exibe a imagem tendencial.

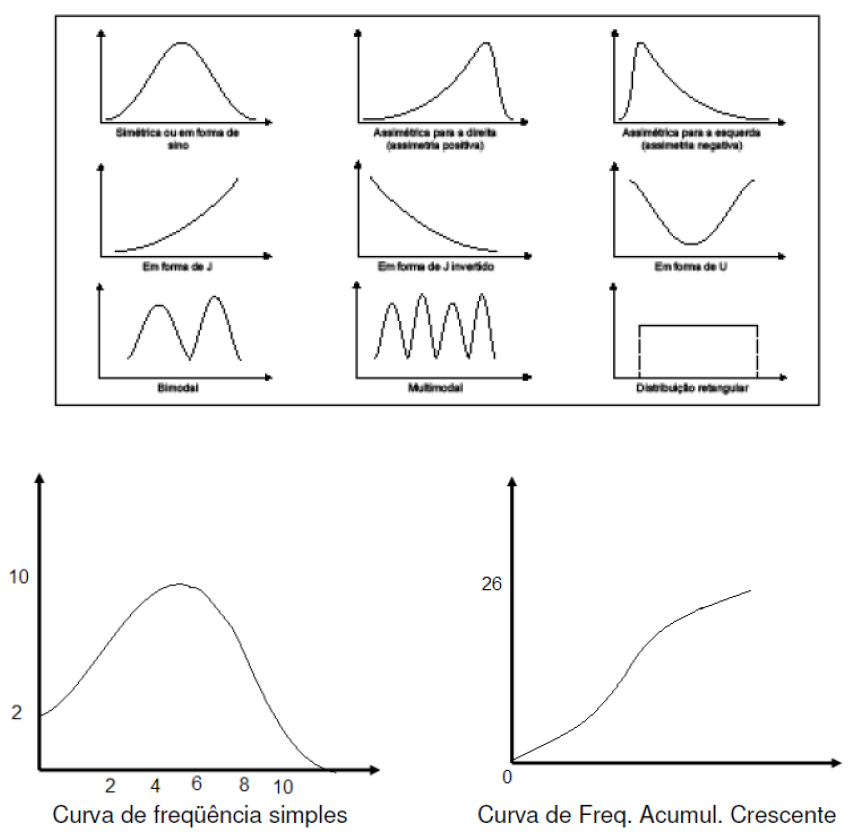
de-to

Após o traçado de um polígono de frequência, é desejável, muitas vezes, que se lhe faça um polimento, de modo a mostrar o que seria tal polígono com um número maior de dados.

Esse procedimento não mostra uma certeza absoluta de que a curva obtida – curva polida – seja tal qual a curva resultante de um grande número de dados.

No entanto, pode-se afirmar que ela assemelha-se mais à curva de frequência do que o polígono de frequência obtido de uma amostra limitada.

O polimento, geometricamente, corresponde à eliminação dos vértices da linha poligonal.

Consegue-se isso com o emprego de uma fórmula bastante simples, a qual, a partir das frequências reais, nos fornece novas frequências – frequências calculadas – que se localizarão, como no polígono de frequências, nos pontos médios.

A fórmula para se determinar a frequência calculada ($fc_i$) é:

$fc_i$ = $\frac{f_i + 2 f_{i-1} + f_{i+1}}{4}$

Para cada classe temos que:

  • $fc_i$ é a frequência calculada
  • $f_i$ é a frequência simples
  • $f_{i-1}$ é a frequência simples da classe anterior
  • $f_{i+1}$ é a frequência simples da classe posterior

5.8.1 - As formas das curvas de frequência

As curvas de frequência assumem diferentes formas características.

5.8.1.1 - Curvas em forma de Sino

São muitos os fenômenos que oferecem distribuições em forma de sino: a estatura de adultos, o peso de adultos, a inteligência medida em testes mentais, os preços relativos. Tais curvas podem ser simétricas ou assimétricas.

  • Curva simétrica: essa curva caracteriza-se por apresentar valor máximo no ponto central e os pontos equidistantes desse ponto terem a mesma frequência. As curvas em forma de sino caracterizam-se pelo fato de apresentarem um valor máximo na região central.
  • Curva assimétrica: na prática, não são encontradas distribuições perfeitamente simétricas. Raramente o valor máximo estará exatamente na região central.

As distribuições obtidas de medições reais são mais ou menos assimétricas, em relação à frequência máxima.

Assim, as curvas correspondentes a tais distribuições apresentam a cauda de um lado da ordenada máxima mais longa do que o outro.

Se a cauda mais alongada fica à direita, a curva é chamada assimétrica positiva ou enviesada à direita. Se a curva se alonga à esquerda, a curva é chamada assimétrica negativa ou enviesada à esquerda.

5.8.1.2 - Curvas em forma de Jota

São curvas comuns aos fenômenos econômicos e financeiros: distribuição de vencimentos ou rendas pessoais.

As curvas em forma de jota são relativas a distribuições extremamente assimétricas, caracterizadas por apresentarem o ponto de ordenada máxima em uma das extremidades.

Observação: Um importante exemplo das curvas em J, na área econômica, é a Curva de Lorenz, que é um gráfico utilizado para representar distribuição de rendas ou de riquezas etc.

Exemplo: desigualdade de renda familiar per capita no Brasil.

5.8.1.3 - Curvas em forma de U

As curvas em forma de U são caracterizadas por apresentarem ordenadas máximas em ambas as extremidades.

Como exemplo de distribuição que dá origem a esse tipo de curva pode-se citar a de mortalidade por idade.

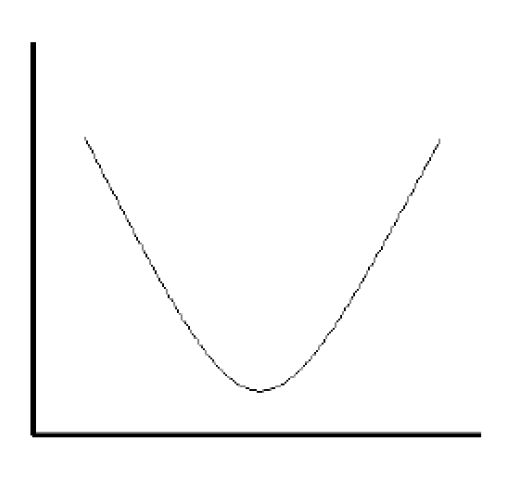
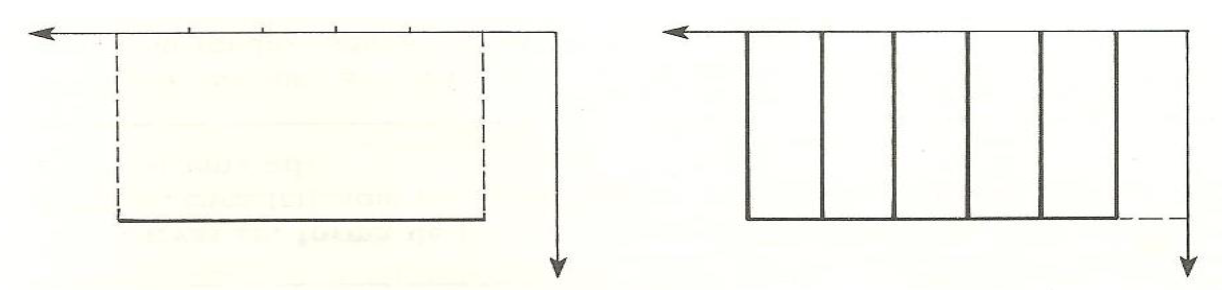
5.8.1.4 - Distribuição Retangular

Essa distribuição, muito rara na verdade, apresenta todas as classes com a mesma frequência.

Tal distribuição seria representada por um histograma em que todas as colunas teriam a mesma altura ou por um polígono de frequência reduzido a um segmento de reta horizontal.

Exemplo: tabela com o montante de pagamentos efetuados em um banco durante um dia.

Montante (R$) Frequência
500 |-- 1000 28
1000 |-- 1500 12
1500 |-- 2000 32
2000 |-- 2500 50
2500 |-- 3000 38
3000 |-- 3500 32
3500 |-- 4000 7

Arduino
Coautor
Betobyte
Autor
Autores
||| Áreas ||| Estatística ||| Python ||| Projetos ||| Dicas & Truques ||| Quantum ||| Estatística Básica || Estatística Básica || Estatistica Avançada || Bayes || Aulas | Conceitos Fundamentais (Conceitos fundamentais e compreensão da estatística, tratando da coleta, da análise, da interpretação e da apresentação de massas de dados numéricos, também significando um conjunto de dados numéricos.) | População e Amostra (População e amostra como um conjuntos de objetos, itens ou eventos com alguma característica ou propriedade comum mensurável, ordenável ou comparável de acordo com os limites propostos e objetivos do estudo.) | Séries Estatísticas (Séries estatísticas como distribuição de conjuntos de dados estatísticos em função da época, do local ou da espécie (fenômeno).) | Gráficos Estatísticos (Representação gráfica estabelecendo correspondência entre os termos da série e determinada figura geométrica, de tal modo que cada elemento da série seja representado por uma figura proporcional.) | Distribuição de Frequência (Distribuição de Frequência como conjunto de dados em uma tabela conforme as frequências ou repartições de seus valores, podendo ser discreta ou contínua de uma série estatística em que permanecem constantes o fato, o local e a época em que o fenômeno ocorreu.) | Medidas de Posição (Medidas de posição com a localização da maior concentração de valores de uma distribuição, isto é, se ela se localiza no início, no meio ou no final, ou, ainda, se há uma distribuição por igual.) | Medidas de Dispersão (Medidas de dispersão ou variabilidade empregadas na descoberta do grau de variabilidade ou dispersão dos valores observados em torno da média aritmética, medindo a representatividade da média e destacam o nível de homogeneidade ou heterogeneidade dentro de cada grupo estatístico analisado.) | Medidas de Assimetria/Curtose (Medidas de forma por descreverem a forma da curva de distribuição dos dados, indicando o grau de assimetria de uma distribuição de frequências unimodal em relação a uma linha vertical que passa por seu ponto mais elevado ou o grau de achatamento de uma distribuição em relação a distribuição padrão denominada curva normal.) | Probabilidade (O cálculo de probabilidades é uma necessidade essencial para o estudo de Estatística Indutiva (ou Inferencial) pelo fato de a maioria dos fenômenos tratados na Estatística serem de natureza aleatória ou probabilística.) | Distribuição Binomial (A probabilidade de ocorrerem k sucessos e (n–k) fracassos dada pelo termo geral do Binômio de Newton.) |