6 - Métricas de Avaliação de Modelos
As métricas de avaliação são usadas para medir o desempenho e a eficácia de modelos de Aprendizado de Máquina em tarefas de classificação e outras tarefas de previsão, proporcionando avaliar a qualidade das previsões do modelo e entender sua capacidade de generalização para novos dados.
Algumas das métricas mais comuns incluem:
- Precisão (Precision): A precisão é a proporção de exemplos positivos corretamente classificados em relação a todos os exemplos classificados como positivos (verdadeiros positivos e falsos positivos). Uma alta precisão indica que o modelo tem poucos falsos positivos, ou seja, ele é bom em classificar corretamente os exemplos positivos, mas pode ter muitos falsos negativos. Fórmula: $precisão = \frac{TP}{TP + FP}$
- Revocação (Recall ou Sensibilidade): A revocação é a proporção de exemplos positivos corretamente classificados em relação a todos os exemplos positivos no conjunto de dados (verdadeiros positivos e falsos negativos).Uma alta revocação indica que o modelo é bom em identificar a maioria dos exemplos positivos, mas pode gerar muitos falsos positivos. Fórmula: $revocação = \frac{TP}{TP + FN}$
- Escore F1 (F1S - F1 Score): O escore F1 é uma métrica que combina precisão e revocação em uma única medida. É a média harmônica entre a precisão e a revocação.O escore F1 é útil quando há um desequilíbrio significativo entre as classes, pois equilibra a importância das duas métricas. Fórmula: ${f1s} = 2 . \frac{precisão _x revocação}{precisão + revocação}$.
- Acurácia (Accuracy): A acurácia é a proporção de exemplos corretamente classificados em relação ao total de exemplos no conjunto de dados. A acurácia é uma métrica geral que funciona bem quando as classes são balanceadas, mas pode ser enganosa quando há um desequilíbrio significativo entre as classes. Fórmula: $acurácia = \frac{TP + TN}{TP + TN + FP + FN}$.
- Especificidade (Specificity): A especificidade é a proporção de exemplos negativos corretamente classificados em relação a todos os exemplos negativos no conjunto de dados (verdadeiros negativos e falsos positivos). A especificidade é especialmente importante quando a classe negativa é a classe de interesse. Fórmula: $especificidade = \frac{TN}{TN + FP}$
- Erro Quadrático Médio (MSE - Mean Squared Error): MSE é uma métrica comumente usada em problemas de regressão. Ele mede o erro médio quadrático entre as previsões do modelo e os valores reais. Fórmula: $mse = \sum_{(i=0)}^n {(alvo_{verdadeiro} - alvo_{previsto})^2}$, onde $alvo_{verdadeiro}$ representa os valores reais do conjunto de dados e $alvo_{previsto}$ representa as previsões feitas pelo modelo.
- Matriz de Confusão (CM - Confusion Matrix): CM é uma tabela usada para avaliar o desempenho de um modelo de Aprendizado de Máquina em problemas de classificação
- Curva ROC (Receiver Operating Characteristic) e Área Sob a Curva (AUC - Area Under the Curve): Métricas de avaliação muito utilizadas em problemas de classificação binária.
É importante selecionar a métrica de avaliação adequada para cada problema específico, levando em consideração as características dos dados, o desequilíbrio de classes e os objetivos do projeto.
Por exemplo, em problemas de detecção de fraudes, é importante ter alta revocação, mesmo que isso signifique sacrificar a precisão.
Além disso, é recomendado usar mais de uma métrica de avaliação para obter uma compreensão completa do desempenho do modelo.
6.1 - Precisão
A precisão (precision) é a proporção de exemplos positivos corretamente classificados em relação a todos os exemplos classificados como positivos (verdadeiros positivos e falsos positivos).
A precisão é uma métrica de avaliação de classificação que mede a proporção de exemplos positivos corretamente classificados em relação a todos os exemplos classificados como positivos (verdadeiros positivos e falsos positivos).
Uma alta precisão indica que o modelo tem poucos falsos positivos, ou seja, é bom em classificar corretamente os exemplos positivos. No entanto, uma alta precisão pode ocorrer em detrimento da revocação, ou seja, o modelo pode ter muitos falsos negativos.
Nesse caso, a maioria das classificações positivas do modelo é realmente correta. Por outro lado, uma baixa precisão indica que o modelo tem muitos falsos positivos, ou seja, classifica exemplos negativos como positivos com frequência.
Em outras palavras, a precisão nos diz a capacidade do modelo de identificar corretamente os verdadeiros positivos em relação ao total de classificações positivas que ele fez.
A fórmula para calcular a precisão é: $precisão = \frac{TP}{TP + FP}$, onde $TP$ (True Positives) representa a quantidade de exemplos positivos que foram corretamente classificados como positivos pelo modelo e $FP$ (False Positives) representa a quantidade de exemplos negativos que foram incorretamente classificados como positivos pelo modelo.
A precisão é especialmente relevante quando o custo dos falsos positivos é alto e deve ser minimizado.
Por exemplo, em um sistema de detecção de fraudes em transações financeiras, um falso positivo pode resultar no bloqueio indevido de uma transação legítima, causando inconveniência ao usuário. Nesse caso, é importante ter alta precisão para garantir que as transações genuínas sejam identificadas corretamente.
No entanto, é importante observar que a precisão pode não ser suficiente para avaliar completamente o desempenho de um modelo, especialmente em casos de desequilíbrio de classes. Um modelo que tenha alta precisão, mas baixa revocação (ou seja, alto número de falsos negativos), pode ser inadequado em situações em que é essencial identificar a maioria dos exemplos positivos corretamente.
Em resumo, a precisão é uma métrica importante para avaliar o desempenho de um modelo de classificação, mas deve ser interpretada em conjunto com outras métricas, como a revocação, o F1-Score e a acurácia, para obter uma visão mais completa da capacidade do modelo em classificar corretamente as diferentes classes.
O exemplo abaixo calcula a precisão usando a biblioteca Scikit-Learn.
# Importe as bibliotecas necessárias
from sklearn.metrics import precision_score
# Dados de exemplo
alvo_verdadeiro = [1, 0, 1, 1, 0, 1, 0, 0, 1, 0] # Rótulos verdadeiros
alvo_previsto = [1, 0, 1, 0, 1, 1, 0, 1, 1, 0] # Rótulos previstos
# Suponha que você tenha as previsões do seu modelo (alvo_previsto) e os rótulos reais (alvo_verdadeiro)
# Calcule a precisão
precision = precision_score(alvo_verdadeiro, alvo_previsto)
print(f'Precisão (Precision): {precision:.4f}')Lembre-se de substituir alvo_verdadeiro e alvo_previsto pelos seus próprios valores reais e previsões.
A precisão é especialmente útil quando você deseja ter certeza de que as previsões positivas do seu modelo são confiáveis, ou seja, quando é importante minimizar falsos positivos. A precisão também varia de 0 a 1, onde um valor mais alto indica um melhor desempenho do modelo em fazer previsões positivas precisas.
6.2 - Revocação
A revocação (recall ou sensibilidade) é a proporção de exemplos positivos corretamente classificados em relação a todos os exemplos positivos no conjunto de dados (verdadeiros positivos e falsos negativos).
A revocação é uma métrica de avaliação de classificação que mede a proporção de exemplos positivos corretamente classificados em relação a todos os exemplos positivos no conjunto de dados (verdadeiros positivos e falsos negativos). Em outras palavras, a revocação nos diz a capacidade do modelo de identificar corretamente os verdadeiros positivos em relação ao total de exemplos positivos presentes no conjunto de dados.
A fórmula para calcular a revocação é: $revocação = \frac{TP}{TP + FN}$, onde $TP$ (True Positives) representa a quantidade de positivos verdadeiros, ou seja, exemplos positivos que foram corretamente classificados como positivos pelo modelo, e $FN$ (False Negatives) representa a quantidade de falsos negativos, ou seja, exemplos positivos que foram incorretamente classificados como negativos pelo modelo.
Uma alta revocação indica que o modelo é bom em identificar a maioria dos exemplos positivos, ou seja, ele possui a habilidade de "lembrar" de uma grande proporção dos exemplos positivos presentes no conjunto de dados. No entanto, uma alta revocação pode ocorrer em detrimento da precisão, ou seja, o modelo pode gerar muitos falsos positivos.
Por outro lado, uma baixa revocação indica que o modelo tem muitos falsos negativos, ou seja, não consegue identificar corretamente muitos dos exemplos positivos existentes no conjunto de dados.
A revocação é especialmente relevante quando o custo dos falsos negativos é alto e deve ser minimizado. Em certos cenários, como em um sistema de diagnóstico médico, um falso negativo pode resultar em não identificar uma condição médica séria, o que pode ter graves consequências para o paciente. Nesse caso, é importante ter alta revocação para garantir que a maioria dos casos positivos seja detectada corretamente.
No entanto, assim como acontece com a precisão, é essencial observar que a revocação pode não ser suficiente para avaliar completamente o desempenho de um modelo de classificação. Um modelo que tenha alta revocação, mas baixa precisão (ou seja, alto número de falsos positivos), pode ser inadequado em situações em que é essencial minimizar os falsos positivos.
Em resumo, a revocação é uma métrica importante para avaliar o desempenho de um modelo de classificação, mas deve ser interpretada em conjunto com outras métricas, como a precisão, o F1-Score e a acurácia, para obter uma visão mais completa da capacidade do modelo em classificar corretamente as diferentes classes.
Exemplo:
A revocação (recall), também conhecida como taxa de verdadeiros positivos, é uma métrica importante em problemas de classificação, especialmente quando estamos interessados em minimizar falsos negativos.
Aqui está um código Python para calcular a revocação usando a biblioteca Scikit-Learn:
# Importe as bibliotecas necessárias
from sklearn.metrics import recall_score
# Dados de exemplo
alvo_verdadeiro = [1, 0, 1, 1, 0, 1, 0, 0, 1, 0] # Rótulos verdadeiros
alvo_previsto = [1, 0, 1, 0, 1, 1, 0, 1, 1, 0] # Rótulos previstos
# Suponha que você tenha as previsões do seu modelo (alvo_previsto) e os rótulos reais (alvo_verdadeiro)
# Calcule a revocação
recall = recall_score(alvo_verdadeiro, alvo_previsto)
print(f'Revocação (Recall): {recall:.4f}')Lembre-se de substituir alvo_verdadeiro e alvo_previsto pelos seus próprios valores reais e previsões.
A revocação é especialmente útil quando você deseja minimizar falsos negativos, ou seja, quando classificar erroneamente algo como negativo quando na verdade é positivo é problemático. A revocação varia de 0 a 1, onde um valor mais alto indica um melhor desempenho do modelo em identificar verdadeiros positivos.
6.3 - Escore-F1
O Escore-F1 (F1S - F1 Score) é a média harmônica entre a precisão e a revocação, uma métrica de avaliação de classificação que combina a precisão e a revocação (ou sensibilidade) em uma única medida, fornecendo uma medida geral do desempenho do modelo, especialmente quando há um desequilíbrio significativo entre as classes, sendo uma métrica útil quando existe um trade-off entre precisão e revocação.
Em algumas situações, aumentar a precisão do modelo pode resultar em uma diminuição da revocação e vice-versa. O Escore-F1 é uma média harmônica entre precisão e revocação, e ele busca encontrar um equilíbrio entre essas duas métricas.
É útil quando há um desequilíbrio significativo entre as classes, quando é necessário encontrar um equilíbrio entre a identificação correta de exemplos positivos e a minimização de falsos positivos e falsos negativos, portanto equilibrando a importância das duas métricas.
O Escore-F1 varia de 0 a 1, sendo que o valor de 1 representa o melhor desempenho possível, indicando um modelo que tem alta precisão e alta revocação simultaneamente. Quanto mais próximo de 1 o Escore-F1 estiver, melhor o desempenho geral do modelo.
A fórmula para calcular o Escore-F1 é: $f1s = 2 . \frac{precisão . revocação}{precisão + pevocação}$, onde $Precisão$ é a proporção $\frac{TP}{TP + FP}$ de casos positivos corretamente classificados em relação a todos os casos classificados como positivos, e $revocação$ é a proporção $\frac{TP}{TP + FN}$ de casos positivos corretamente classificados em relação a todos os exemplos positivos no conjunto de dados.
O Escore-F1 é especialmente útil quando as classes estão desequilibradas, ou seja, quando uma classe possui muito mais exemplos do que a outra. Nesses casos, um modelo que possui alta precisão, mas baixa revocação, ou vice-versa, pode fornecer uma visão distorcida do seu desempenho. O F1-Score busca resolver essa questão, fornecendo uma medida única que equilibra a importância de identificar corretamente ambas as classes.
No entanto, é importante considerar o contexto específico do problema. Em algumas situações, a precisão pode ser mais importante do que a revocação, ou vice-versa, e, nesses casos, o F1-Score pode não ser a métrica mais adequada. Portanto, é recomendado utilizar o F1-Score em conjunto com outras métricas, como a acurácia, a precisão e a revocação, para obter uma avaliação mais completa do desempenho do modelo em diferentes cenários.
# Importe as bibliotecas necessárias
from sklearn.metrics import f1_score
# Dados de exemplo
alvo_verdadeiro = [1, 0, 1, 1, 0, 1, 0, 0, 1, 0] # Rótulos verdadeiros
alvo_previsto = [1, 0, 1, 0, 1, 1, 0, 1, 1, 0] # Rótulos previstos
# Calcule o F1-Score
f1 = f1_score(alvo_verdadeiro, alvo_previsto)
print(f'F1-Score: {f1:.4f}')Lembre-se de substituir alvo_verdadeiro e alvo_previsto pelos seus próprios valores reais e previsões.
O F1-Score é especialmente útil quando você deseja encontrar um equilíbrio entre precisão e recall, e pode ser particularmente útil em cenários onde as classes estão desequilibradas.
Ele varia de 0 a 1, onde um valor mais alto indica um melhor desempenho do modelo.
6.4 - Acurácia
A acurácia (accuracy) é a proporção de casos corretamente classificados em relação ao total de casos no conjunto de dados, uma métrica geral que funciona bem quando as classes são balanceadas e indica o quão bem o modelo está realizando suas previsões em geral.
Uma alta acurácia indica que o modelo está corretamente classificando a maioria dos casos, tanto positivos quanto negativos, em relação ao total de casos do conjunto de dados sendo particularmente útil quando as classes estão balanceadas, ou seja, quando o número de casos positivos é aproximadamente igual ao número de casos negativos. Nesse cenário, a acurácia pode ser uma métrica confiável para avaliar o desempenho do modelo.
No entanto, ela pode ser enganosa quando há um desequilíbrio significativo entre as classes, levando a uma avaliação inadequada do desempenho do modelo.
A acurácia é uma métrica de avaliação de classificação que mede a proporção de casos corretamente classificados em relação ao total de casos no conjunto de dados.
Em outras palavras, a acurácia nos diz a capacidade do modelo de fazer previsões corretas para todas as classes presentes no conjunto de dados.
A fórmula para calcular a acurácia é: $acurácia = \frac{TP + TN}{TP + TN + FP + FN}$, onde: $TP$ (True Positives) é a quantidade de casos positivos corretamente classificados como positivos, $TN$ (True Negatives) é a quantidade de casos negativos que foram corretamente classificados como negativos, $FP$ (False Positives) é a quantidade de casos negativos que foram incorretamente classificados como positivos e $FN$ (False Negatives) é a quantidade de casos positivos que foram incorretamente classificados como negativos.
A acurácia é amplamente utilizada como uma métrica de referência para avaliar a eficácia geral de um modelo de classificação, especialmente quando não há uma classe específica com maior importância ou quando todas as classes têm o mesmo peso.
No entanto, é importante observar que a acurácia pode ser enganosa quando as classes estão desequilibradas, ou seja, quando uma classe possui muito mais casos do que a outra. Nesses casos, um modelo que prevê apenas a classe majoritária pode alcançar alta acurácia, mas ainda assim não ser eficaz em identificar corretamente a classe minoritária. Nesse contexto, outras métricas, como o F1-Score, podem ser mais apropriadas para avaliar o desempenho do modelo.
Em resumo, a acurácia é uma métrica importante para obter uma visão geral do desempenho do modelo de classificação, mas deve ser interpretada com cuidado, especialmente quando há desequilíbrio entre as classes. Em casos de desequilíbrio, é recomendado utilizar outras métricas, como a precisão, a revocação e o F1-Score, para obter uma avaliação mais precisa do desempenho do modelo em diferentes cenários.
Exemplo:
A acurácia é uma métrica comum para avaliar o desempenho geral de um modelo de classificação. Ela mede a proporção de previsões corretas em relação ao total de previsões.
Você pode calcular a acurácia usando o seguinte código Python:
# Importe as bibliotecas necessárias
from sklearn.metrics import accuracy_score
# Dados de exemplo
alvo_verdadeiro = [1, 0, 1, 1, 0, 1, 0, 0, 1, 0] # Rótulos verdadeiros
alvo_previsto = [1, 0, 1, 0, 1, 1, 0, 1, 1, 0] # Rótulos previstos
# Calcule a acurácia
acuracia = accuracy_score(alvo_verdadeiro, alvo_previsto)
print(f'Acurácia: {acuracia:.4f}')Certifique-se de substituir alvo_verdadeiro e alvo_previsto pelos seus próprios valores reais e previsões.
A acurácia é uma métrica útil para ter uma ideia geral de quão bem seu modelo está fazendo em termos de previsões corretas em relação ao total de previsões.
No entanto, é importante observar que a acurácia pode não ser a métrica ideal em todos os cenários, especialmente em problemas desequilibrados, onde uma classe pode dominar numericamente a outra.
Em tais casos, outras métricas, como precisão, recall, F1-score, especificidade, entre outras, podem ser mais informativas.
6.5 - Especificidade
A especificidade (specificity) é uma métrica de avaliação de classificação que mede a proporção de casos negativos corretamente classificados em relação a todos os casos negativos no conjunto de dados (verdadeiros negativos e falsos positivos), sendo especialmente importante quando a classe negativa é a classe de interesse, e o modelo precisa identificar corretamente casos negativos.
Uma alta especificidade indica que o modelo é bom em identificar corretamente a maioria dos casos negativos. Em outras palavras, ele possui a habilidade de "lembrar" da maioria dos casos negativos presentes no conjunto de dados. Por outro lado, uma baixa especificidade indica que o modelo tem muitos falsos positivos, ou seja, classifica casos negativos como positivos com frequência.
Em outras palavras, a especificidade nos diz a capacidade do modelo de identificar corretamente os verdadeiros negativos em relação ao total de casos negativos presentes no conjunto de dados.
A fórmula para calcular a especificidade é: $especificidade = \frac{TN}{TN + FP}$, onde $TN$ (True Negatives) representa a quantidade de casos negativos que foram corretamente classificados como negativos e $FP$ (False Positives) representa a quantidade de casos negativos que foram incorretamente classificados como positivos.
A especificidade é uma métrica importante para avaliar o desempenho do modelo em relação à classe negativa, mas deve ser considerada em conjunto com outras métricas para uma avaliação mais abrangente do modelo em cenários de desequilíbrio de classes ou com requisitos específicos para a classificação correta de casos negativos.
A especificidade é especialmente relevante quando a classe negativa é a classe de interesse e é importante minimizar os falsos positivos. Por exemplo, em um sistema de detecção de doenças raras, uma alta especificidade é crucial para garantir que os resultados positivos sejam altamente confiáveis e que os falsos alarmes sejam reduzidos ao mínimo.
Assim como acontece com as outras métricas de avaliação, a especificidade deve ser interpretada em conjunto com outras métricas, como a precisão, a revocação, o F1-Score e a acurácia, para obter uma avaliação completa do desempenho do modelo de classificação em diferentes cenários.
Exemplo:
# Importe as bibliotecas necessárias
from sklearn.metrics import confusion_matrix
# Dados de exemplo
alvo_verdadeiro = [1, 0, 1, 1, 0, 1, 0, 0, 1, 0] # Rótulos verdadeiros
alvo_previsto = [1, 0, 1, 0, 1, 1, 0, 1, 1, 0] # Rótulos previstos
# Calcula a matriz de confusão
conf_matrix = confusion_matrix(alvo_verdadeiro, alvo_previsto)
# Extrai os elementos da matriz de confusão
verdadeiros_negativos = conf_matrix[0, 0]
falsos_positivos = conf_matrix[0, 1]
# Calcula a especificidade
especificidade = verdadeiros_negativos / (verdadeiros_negativos + falsos_positivos)
print(f'Especificidade: {especificidade:.4f}')Use alvo_verdadeiro e alvo_previsto com pelos seus próprios valores reais e previsões.
A especificidade é uma métrica importante para avaliar o desempenho de um modelo de classificação, especialmente quando você deseja avaliar sua capacidade de identificar corretamente os verdadeiros negativos em um problema desequilibrado.
6.6 - Erro Quadrático Médio
O Erro Quadrático Médio (MSE - Mean Squared Error) é uma métrica de avaliação comumente usada em problemas de regressão, que mede o erro quadrático médio entre as previsões do modelo e os valores reais do conjunto de dados.
O MSE é uma medida que avalia a qualidade das previsões do modelo em relação aos valores reais, calculando a média dos quadrados das diferenças entre as previsões e os valores reais para todos as amostras no conjunto de dados.
A fórmula para calcular o MSE é: $MSE = \frac{\sum_{(i=0)}^n {(ALVO_{verdadeiro} - ALVO_{previsto})^2}}{n}$, onde $ALVO_{verdadeiro}$ representa os valores reais do conjunto de dados, $ALVO_{previsto}$ representa as previsões feitas pelo modelo, $Σ$ indica a soma sobre todos as amostras no conjunto de dados e $n$ é o número total de amostras no conjunto de dados.
Quanto menor o valor do MSE, melhor o desempenho do modelo, pois indica que as previsões estão mais próximas dos valores reais.
O MSE é sensível a valores extremos (outliers) e é especialmente útil quando a distribuição dos erros é importante para a análise do problema de regressão, sendo especialmente útil quando se deseja medir a qualidade das previsões em termos de distância média entre as previsões e os valores reais, penalizando mais fortemente as previsões que estão mais distantes dos valores reais.
O MSE é amplamente utilizado em problemas de regressão, onde o objetivo é prever um valor numérico contínuo. Em tais problemas, é importante minimizar o erro entre as previsões e os valores reais. Fornece uma medida objetiva desse erro, permitindo que se comparem diferentes modelos e escolha o modelo que melhor se ajusta aos dados. No entanto, é importante notar que a interpretação do MSE pode variar dependendo do contexto do problema.
Por exemplo, um MSE de 100 pode ser considerado bom em um problema onde os valores reais variam de 0 a 1000, mas pode ser ruim em um problema onde os valores reais variam de 0 a 10. Portanto, é recomendado comparar o MSE com outras métricas relevantes e considerar o contexto específico do problema para uma avaliação mais completa do desempenho do modelo de regressão.
Essas métricas são fundamentais para avaliar o desempenho de modelos de Aprendizado de Máquina e auxiliar na escolha do melhor modelo para uma tarefa específica. Dependendo do contexto do problema, é importante selecionar as métricas mais adequadas para garantir que o modelo atenda aos requisitos e necessidades específicas do domínio de aplicação.
No exemplo a seguir, alvo_verdadeiro representa os rótulos verdadeiros e alvo_previsto representa os rótulos previstos pelo seu modelo.
O código usa a função mean_squared_error() da biblioteca sklearn.metrics para calcular o MSE entre os rótulos verdadeiros e previstos.
Lembre-se de substituir os valores em alvo_verdadeiro e alvo_previsto pelos seus próprios dados para calcular o MSE específico para o seu problema.
import numpy as np
from sklearn.metrics import mean_squared_error
# Dados de exemplo (rótulos verdadeiros e rótulos previstos)
alvo_verdadeiro = np.array([3.0, 2.5, 4.0, 5.1, 6.3])
alvo_previsto = np.array([2.8, 2.7, 3.8, 5.0, 6.2])
# Calcule o Erro Quadrático Médio (MSE)
mse = mean_squared_error(alvo_verdadeiro, alvo_previsto)
# Imprima o valor do MSE
print(f'Erro Quadrático Médio (MSE): {mse:.4f}')O MSE é uma medida que quantifica a qualidade das previsões feitas por um modelo de regressão. Quanto menor o valor do MSE, melhor o desempenho do modelo em fazer previsões precisas. Neste caso, um MSE de 0.0280 é um valor bastante baixo, o que indica que as previsões feitas pelo modelo estão muito próximas dos valores reais.
Em termos práticos, isso significa que o modelo tem um bom desempenho em prever os valores alvo. Por exemplo, se o modelo estivesse sendo usado para prever preços de casas e o MSE fosse 0.0280, isso indicaria que, em média, as previsões do modelo estariam desviadas por apenas 0.0280 unidades quadradas da unidade de medida relevante (como dólares, no caso de preços de casas).
Em resumo, um MSE baixo é indicativo de um modelo preciso, enquanto um MSE alto indicaria que as previsões do modelo estão distantes dos valores reais. Portanto, neste contexto, um MSE de 0.0280 é um bom resultado.
6.7 - Matriz de Confusão
A Matriz de Confusão (CM - Confusion Matrix) é uma tabela usada para avaliar o desempenho de um modelo de Aprendizado de Máquina em problemas de classificação, que permite a visualização do número de previsões corretas e incorretas feitas pelo modelo para cada classe do problema.
A matriz de confusão é especialmente útil quando se trabalha com problemas de classificação binária, ou seja, problemas em que há apenas duas classes a serem previstas, como "sim" ou "não", "positivo" ou "negativo", "verdadeiro" ou "falso", etc. No entanto, ela também pode ser adaptada para problemas de classificação multiclasse.
A matriz de confusão possui quatro elementos principais:
- Verdadeiros Positivos (TP - True Positives): Representa o número de exemplos que foram corretamente classificados como positivos pelo modelo. São os casos em que o modelo previu corretamente a classe positiva.
- Falsos Positivos (FP - False Positives): Representa o número de exemplos que foram erroneamente classificados como positivos pelo modelo. São os casos em que o modelo previu a classe positiva, mas a classe real era negativa.
- Verdadeiros Negativos (TN - True Negatives): Representa o número de exemplos que foram corretamente classificados como negativos pelo modelo. São os casos em que o modelo previu corretamente a classe negativa.
- Falsos Negativos (FN - False Negatives): Representa o número de exemplos que foram erroneamente classificados como negativos pelo modelo. São os casos em que o modelo previu a classe negativa, mas a classe real era positiva.
A matriz de confusão é organizada da seguinte forma:
| Classe Real | ||
| Classe Previsão | Positivo | Negativo |
| Positivo | TP | FP | Negativo | FN | TN |
A partir dos valores na matriz de confusão, podemos calcular diversas métricas de avaliação, como precisão, revocação, F1-Score, acurácia, especificidade, etc.
Essas métricas são fundamentais para entender o desempenho do modelo e a sua capacidade de generalização para novos dados.
A matriz de confusão é uma ferramenta importante para o diagnóstico do desempenho do modelo em diferentes classes e permite uma análise mais detalhada das previsões, auxiliando na identificação de possíveis problemas, como o modelo estando enviesado para uma classe específica ou tendo dificuldade em detectar certas classes.
Exemplo:
Este código cria uma matriz de confusão a partir dos rótulos verdadeiros (alvo_verdadeiro) e dos rótulos previstos (alvo_previsto) e, em seguida, gera um gráfico de calor usando a biblioteca seaborn para visualizar a matriz de confusão.
Certifique-se de substituir alvo_verdadeiro e alvo_previsto pelos seus próprios rótulos verdadeiros e previstos. Isso permitirá que você crie uma matriz de confusão personalizada para a sua tarefa de classificação.
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
import seaborn as sns
# Dados de exemplo
alvo_verdadeiro = [1, 0, 1, 1, 0, 1, 0, 0, 1, 0] # Rótulos verdadeiros
alvo_previsto = [1, 0, 1, 0, 1, 1, 0, 1, 1, 0] # Rótulos previstos
# Crie a matriz de confusão
confusion = confusion_matrix(alvo_verdadeiro, alvo_previsto)
# Crie um gráfico de calor para visualizar a matriz de confusão
plt.figure(figsize=(6, 6))
sns.heatmap(confusion, annot=True, fmt='d', cmap='Blues', cbar=False, square=True, xticklabels=['Negativo', 'Positivo'], yticklabels=['Negativo', 'Positivo'])
plt.xlabel('Previsto')
plt.ylabel('Verdadeiro')
plt.title('Matriz de Confusão')
plt.show()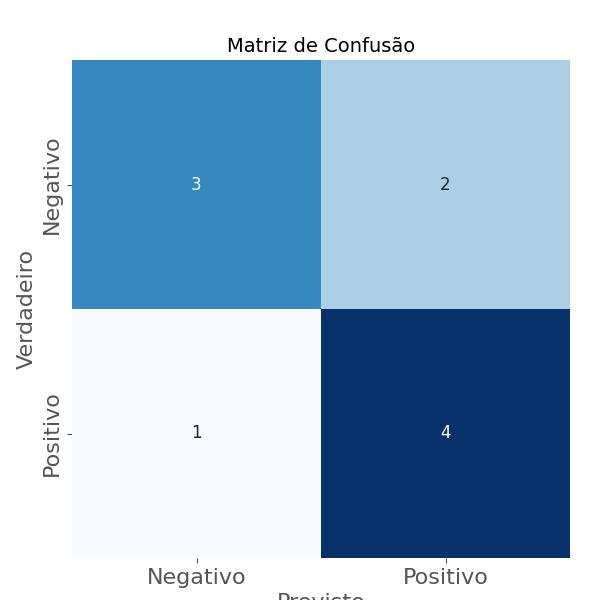
6.8 - Curva ROC e Área Sob a Curva (AUC)
A Curva ROC (Receiver Operating Characteristic) e a Área Sob a Curva (AUC - Area Under the Curve) são métricas de avaliação muito utilizadas em problemas de classificação binária.
A Curva ROC é uma representação gráfica do desempenho do modelo à medida que o limiar de classificação é variado, e a AUC é a área sob essa curva.
Para construir a Curva ROC, o modelo é executado em diferentes limiares de decisão e, para cada limiar, é calculada a taxa de verdadeiros positivos (TPR - True Positive Rate) e a taxa de falsos positivos (FPR - False Positive Rate).
A Curva ROC é criada plotando os valores de TPR (eixo y), em função dos valores de FPR (eixo x) para os diferentes limiares de classificação. Quanto mais próxima a curva ROC estiver do canto superior esquerdo do gráfico, melhor será o desempenho do modelo.
É uma representação gráfica que ilustra a taxa de verdadeiros positivos (revocação) em função da taxa de falsos positivos ao variar o limiar de classificação do modelo.
- Taxa de Verdadeiros Positivos (TPR - True Positive Rate): É a proporção de exemplos positivos corretamente classificados em relação ao total de exemplos positivos (verdadeiros positivos + falsos negativos). Fórmula: $TPR = \frac{TP}{TP + FN}$
- Taxa de Falsos Positivos (FPR - False Positive Rate): É a proporção de exemplos negativos incorretamente classificados como positivos em relação ao total de exemplos negativos (verdadeiros negativos + falsos positivos). Fórmula: $FPR = \frac{FP}{FP + TN}$
A Área Sob a Curva (AUC) é uma métrica numérica que representa a área sob a Curva ROC.
A AUC é um número entre 0 e 1, sendo que um modelo com AUC igual a 1 é considerado perfeito (classifica corretamente todos os exemplos), e um modelo com AUC igual a 0.5 é equivalente a um classificador aleatório.
Em geral, quanto maior a AUC, melhor é o desempenho do modelo na classificação das duas classes.
A AUC é uma métrica útil para problemas de classificação binária, especialmente quando as classes estão desbalanceadas ou quando a taxa de verdadeiros positivos e falsos positivos são igualmente importantes para a avaliação do modelo.
A Curva ROC e a AUC são métricas robustas e amplamente utilizadas para avaliar e comparar o desempenho de diferentes modelos de classificação em problemas binários, permitindo uma avaliação mais abrangente do desempenho do modelo em diferentes limiares de classificação, fornecendo uma visão completa da capacidade de discriminação do modelo entre as classes positiva e negativa.
Exemplo:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_curve, roc_auc_score, auc
data = {
'caracteristica1': np.random.rand(2000),
'caracteristica2': np.random.rand(2000),
'alvo': np.random.randint(0, 2, 2000)
}
df = pd.DataFrame(data)
# Dividindo os dados em conjunto de treinamento e teste
X = df[['caracteristica1', 'caracteristica2']]
y = df['alvo']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Treinando um modelo de regressão logística (você pode substituir por seu próprio modelo)
model = LogisticRegression()
model.fit(X_train, y_train)
# Obtendo as probabilidades previstas para a classe positiva
y_scores = model.predict_proba(X_test)[:, 1]
# Calculando a curva ROC
fpr, tpr, _ = roc_curve(y_test, y_scores)
# Calculando a AUC (Área sob a Curva ROC)
roc_auc = auc(fpr, tpr)
# Plotando a curva ROC
plt.figure(figsize=(8, 6))
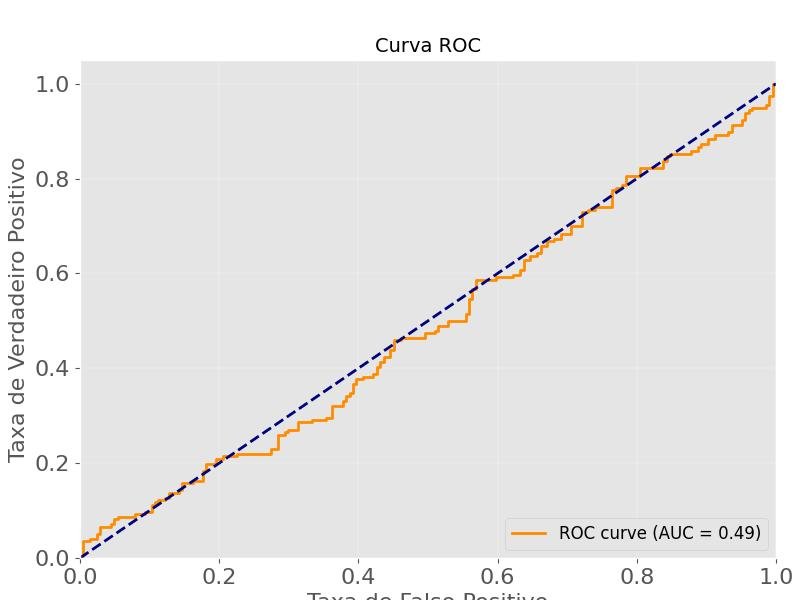
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC curve (AUC = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('Taxa de Falso Positivo')
plt.ylabel('Taxa de Verdadeiro Positivo')
plt.title('Curva ROC')
plt.legend(loc='lower right')
plt.show()