13 - Aprendizado Profundo (DL - Deep Learning)

As Redes Neurais Artificiais (ANN - Artificial Neural Networks) são modelos matemáticos inspirados no funcionamento do cérebro humano, compostos por unidades interconectadas denominadas neurônios artificiais, ou "nós", organizadas em camadas e projetadas para resolver problemas de ML e tarefas de reconhecimento de padrões.

Estes modelos servem de base para várias técnicas de DL e têm sido usadas com sucesso em diversas aplicações.

Cada neurônio recebe entradas ponderadas, aplica uma função de ativação não linear a essas entradas e produz uma saída.

A conexão entre neurônios é representada por pesos, que são ajustados durante o processo de treinamento para que a rede possa aprender a mapear as entradas para as saídas corretas.

Cada neurônio recebe entradas, realiza operações matemáticas nelas e gera uma saída que é transmitida para outros neurônios na rede.

Essa estrutura em camadas é o que permite às ANNs aprenderem a partir dos dados e realizar tarefas complexas, como classificação, regressão, NLP, visão computacional, entre outros.

As ANNs são organizadas com camadas distintas:

• Camada de Entrada: Recebe os dados de entrada e transmite essas informações para a próxima camada. Cada neurônio na camada de entrada representa um recurso ou característica do dado de entrada.
• Camadas Ocultas (Hidden Layers): As camadas ocultas são responsáveis pelo processamento interno dos dados. Cada camada oculta contém um conjunto de neurônios que combinam e transformam as características de entrada para criar representações mais complexas e abstratas dos dados.
• Camada de Saída: É a última camada da rede e produz a saída final do modelo. Dependendo do tipo de tarefa (classificação, regressão, etc.), a camada de saída pode conter um ou mais neurônios.

O processo de treinamento de uma ANN envolve alimentar o modelo com um conjunto de dados de treinamento conhecidos e ajustar os pesos das conexões entre os neurônios para minimizar o erro entre as previsões da rede e as saídas corretas. Isso é geralmente feito usando algoritmos de otimização, como o gradiente descendente, que ajustam os pesos para que a rede possa aprender a representar corretamente os padrões nos dados de treinamento.

As ANNs têm sido aplicadas em uma ampla variedade de tarefas, como classificação de imagens, reconhecimento de fala, NLP, previsão de séries temporais, entre outras. Com o avanço das técnicas de DL, as ANNs têm se mostrado particularmente eficazes em tarefas que envolvem grandes volumes de dados e problemas complexos.

Um dos desafios do uso de ANNs é a necessidade de grandes quantidades de dados de treinamento e poder computacional para ajustar os milhões de pesos da rede. No entanto, com os avanços tecnológicos e o acesso a GPUs e TPUs, as ANNs têm se mostrado cada vez mais poderosas em uma variedade de aplicações, tornando-se uma das ferramentas mais importantes e impactantes no campo do ML e da Inteligência Artificial.

A seguir, apresentamos alguns conceitos importantes relacionados às Redes Neurais Artificiais:

• Neurônio Artificial: O neurônio artificial é a unidade básica de uma ANN. Cada neurônio recebe uma ou mais entradas e aplica uma função de ativação à soma ponderada dessas entradas. A saída do neurônio é transmitida para os neurônios nas camadas subsequentes ou é a saída final da rede, dependendo do tipo de ANN.
• Estrutura: Composta por camadas de neurônios totalmente conectados, adequada para uma variedade de tarefas, mas não lida com sequências ou dados de grade.
• Aplicação: Usadas em tarefas diversas, incluindo classificação de texto, regressão e processamento de linguagem natural.
• Camadas: As ANNs são organizadas em camadas, geralmente divididas em três tipos principais: camada de entrada, camadas ocultas (pode haver várias) e camada de saída. A camada de entrada recebe os dados brutos como entrada, as camadas ocultas são responsáveis por aprender e representar características complexas dos dados, e a camada de saída produz as previsões ou resultados finais.
• Conexões e Pesos: Cada neurônio está conectado a todos os neurônios da camada anterior e da camada seguinte (se houver). Cada conexão tem um peso associado, que representa a força da influência da saída de um neurônio na entrada do outro neurônio. Os pesos são ajustados durante o processo de treinamento da rede para melhorar o desempenho do modelo.
• Funções de Ativação: Cada neurônio aplica uma função de ativação em sua saída antes de transmiti-la aos neurônios na próxima camada. A função de ativação introduz a não-linearidade na rede, permitindo que ela aprenda relações complexas nos dados. Algumas funções de ativação comuns são a função sigmoide, a função ReLU - Rectified Linear Unit (Unidade Linear Retificada) e a função tangente hiperbólica.
• Propagação Direta (Feedforward) e Retropropagação (Backpropagation): O processo de treinamento em uma ANN geralmente é feito usando a técnica de propagação direta e retropropagação. A propagação direta é a etapa de fazer a propagação das entradas pela rede, obtendo as previsões. Em seguida, é calculada a perda (ou erro) entre as previsões da rede e os rótulos reais do conjunto de treinamento. A retropropagação é a etapa de ajustar os pesos das conexões para minimizar a perda, usando técnicas de otimização, como o gradiente descendente.
• Arquitetura e Hiperparâmetros: A escolha da arquitetura da rede, incluindo o número de camadas ocultas, o número de neurônios em cada camada e as funções de ativação, é um dos desafios em projetar uma ANN. Além disso, hiperparâmetros como a taxa de aprendizado, o número de episódios de treinamento e o tamanho do lote também afetam o desempenho do modelo.
• Convolução/Recorrência: Não incorporam convolução ou recorrência; camadas densamente conectadas.
• Uso de Memória: Não mantêm memória de longo prazo; operações independentes.
• Paralelismo: Altamente paralelizáveis, eficazes em hardware acelerado.

As ANNs são uma das ferramentas mais poderosas do ML moderno e têm alcançado resultados impressionantes em uma variedade de domínios.

No entanto, treinar redes neurais profundas pode exigir grandes quantidades de dados e poder computacional, mas com os avanços em hardware e algoritmos, as ANNs continuam sendo objeto de pesquisa intensiva e são amplamente utilizadas em problemas complexos de aprendizado.

As Redes Neurais Convolucionais (CNNs - Convolutional Neural Networks) são um tipo especializado de ANNs que se destacam em tarefas de visão computacional, como classificação de imagens, detecção de objetos e segmentação semântica.

Elas foram inspiradas pela organização do córtex visual no cérebro humano e têm demonstrado um desempenho impressionante em diversas aplicações.

As CNNs são projetadas para trabalhar com dados que têm uma estrutura espacial, como imagens, e têm a capacidade de aprender representações hierárquicas e invariantes da translação de características dos dados.

Isso é possível devido a duas operações principais que as CNNs empregam: convolução e agrupamento (pooling).

Conceitos das CNNs:

• Aplicação: Usadas principalmente em visão computacional para classificação de imagens, detecção de objetos e processamento de imagens.
• Estrutura: Projetadas para dados de grade, como imagens, com camadas de convolução que preservam a estrutura espacial. Usam convolução para extrair características espaciais em dados de grade.
• Arquitetura: As CNNs geralmente têm uma arquitetura empilhada com várias camadas de convolução, seguidas por camadas de agrupamento e camadas totalmente conectadas no final. Algumas arquiteturas famosas incluem a LeNet, AlexNet, VGG, ResNet, Inception e muitas outras.
• Uso de Memória: Não possuem memória interna; operações locais.
• Paralelismo: Paralelismo limitado nas camadas de convolução.

Camadas nas CNNs:

• Camada de Convolução (Conv2D): Essa camada aplica filtros de convolução a uma entrada para extrair características locais em imagens, como bordas, texturas e padrões mais complexos e outros atributos importantes para a tarefa de classificação ou detecção. A convolução é a operação central em uma CNN. Ela consiste em aprender aplicando um conjunto de filtros (ou kernels) sobre a imagem de entrada para extrair características relevantes. Os filtros são pequenas janelas deslizantes que se movem pela imagem, calculando o produto escalar entre si e a região da imagem que está sendo analisada. Isso produz um mapa de características que ressalta padrões específicos presentes na imagem.
• Camadas de Agrupamento (Pooling) (MaxPooling2D, AveragePooling2D): As camadas de agrupamento (pooling, também conhecidas como camadas de subamostragem) são usadas para reduzir a dimensionalidade dos mapas de características, reduzindo a resolução espacial, mantendo as características mais relevantes e tornar a rede computacionalmente mais eficiente. A operação de agrupamento, geralmente agrupamento máximo (max pooling), seleciona o valor máximo em uma região da imagem, descartando o restante. Isso ajuda a preservar as informações mais relevantes e a reduzir o efeito da variação espacial. O MaxPooling2D, por exemplo, mantém o valor máximo em uma região, enquanto o AveragePooling2D usa a média.
• Camada de Normalização de Lotes (Batch Normalization): Essa camada normaliza os valores nas camadas anteriores, o que pode acelerar o treinamento e torná-lo mais estável.
• Camada de Ativação (ReLU): A função de ativação ReLU - Rectified Linear Unit (Unidade Linear Retificada) é frequentemente usada após as camadas de convolução e outras para introduzir não linearidade na rede.
• Camadas Totalmente Conectadas (Dense): Em redes profundas, as Camadas Totalmente Conectadas (Fully Connected Layers) são camadas densas totalmente conectadas, usadas para realizar classificação final ou outras tarefas. Após as camadas de convolução e de agrupamento, os dados são achatados e alimentados em camadas totalmente conectadas, semelhantes às utilizadas em redes neurais tradicionais. Essas camadas finais são responsáveis por fazer a classificação ou regressão com base nas características extraídas anteriormente.

Podemos observar como funciona uma CNN na prática com o diagrama abaixo:

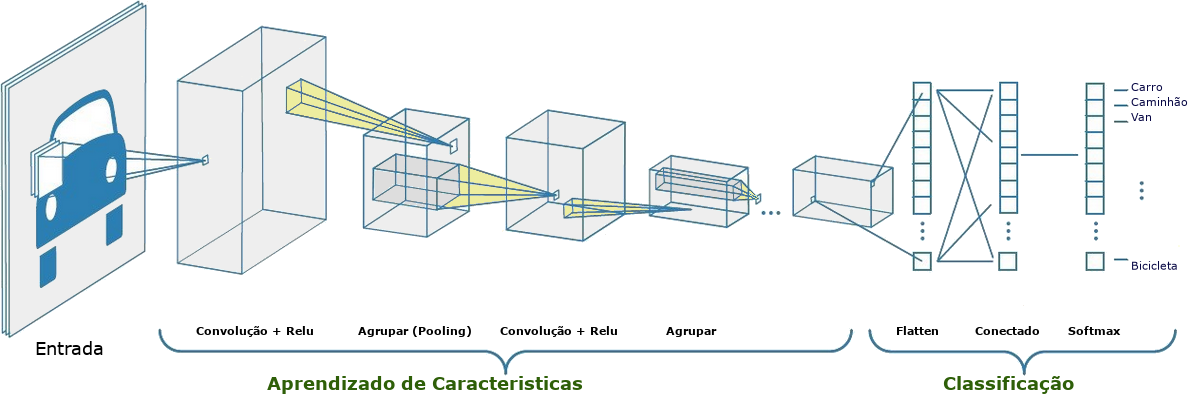
Na primeira etapa, entrada, a rede irá receber uma imagem já pré-processada, geralmente a imagem é representada em 3 camadas RGB ou em tons de cinza.

Em seguida, na etapa de aprendizado de características (feature learning), estas serão aprendidas pelos processos de convolução e agrupamento.

O processo de convolução consiste em utilizar um filtro, também chamado de kernel, para percorrer várias pequenas matrizes na imagem e identificar suas características mais importantes.

Quanto ao agrupamento (pooling), que pode ser interpretado como uma camada simplificadora da camada anterior, atua reduzindo o tamanho dos mapas de características gerados pelas camadas de convolução, para que o processo seja otimizado no decorrer da rede.

Na última etapa, classificação, a rede usará um Perceptron de Múltiplas Camadas (MLP - Multi-Layer Perceptron), ou uma camada totalmente conectada, para realizar a classificação baseando-se nas características obtidas na etapa de aprendizagem de características.

Perceptrons de múltiplas camadas são uma classe de redes neurais artificiais que consistem em múltiplas camadas de neurônios interconectados, incluindo uma camada de entrada, uma ou mais camadas ocultas e uma camada de saída. Cada neurônio em uma camada está conectado a todos os neurônios na camada seguinte, tornando os MLPs capazes de aprender representações complexas de dados. São amplamente utilizados para tarefas de classificação, regressão e outras tarefas de aprendizado supervisionado, devido à sua capacidade de modelar relações não lineares nos dados. O treinamento de MLPs geralmente envolve algoritmos de retropropagação, que ajustam os pesos das conexões para minimizar uma função de perda, permitindo que o modelo faça previsões precisas.

Aqui está um exemplo de como as classes de camadas do Keras podem ser usadas em uma arquitetura de CNN:

from tensorflow.keras.layers import Conv2
from tensorflow.keras.layers import MaxPooling2D
from tensorflow.keras.layers import Flatten
from tensorflow.keras.layers import Dense
from tensorflow.keras.models import Sequential
from tensorflow.keras.datasets import mnist

(x_treino, y_treino), (x_teste, y_teste) = mnist.load_data()

modelo = Sequential()

modelo.add(Conv2(32, (3, 3), activation='relu', input_shape=(28, 28, 1)))
modelo.add(MaxPooling2D((2, 2)))
modelo.add(Flatten())
modelo.add(Dense(128, activation='relu'))
modelo.add(Dense(10, activation='softmax'))

modelo.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])

modelo.fit(x_treino, y_treino, epochs=10)

modelo.evaluate(x_teste, y_teste)

modelo.predict(x_teste)

As CNNs têm tido um impacto significativo em tarefas de visão computacional e se mostraram altamente eficazes em reconhecimento de padrões em imagens.

Além disso, suas arquiteturas têm sido adaptadas para outros tipos de dados estruturados, como séries temporais e dados de áudio.

Devido ao seu poder de representação e aprendizado de características relevantes, as CNNs são amplamente utilizadas em uma variedade de aplicações, desde carros autônomos até diagnóstico médico e muito mais.

As Redes Neurais Recorrentes (RNNs - Recurrent Neural Networks) são um tipo especializado de ANN projetadas para lidar com dados sequenciais, como séries temporais, texto e fala. A principal característica das RNNs é a capacidade de lidar com sequências de comprimentos variáveis, mantendo uma memória interna que permite que elas considerem informações contextuais de eventos anteriores ao processar o próximo elemento da sequência.

Diferentemente das CNNs, que são altamente eficazes para dados com estrutura espacial, as RNNs são projetadas para dados com dependências temporais e são especialmente adequadas para problemas que envolvem previsão, classificação ou geração de sequências.

Conceitos das RNNs:

• Aplicação: Aplicadas a tarefas que envolvem sequências, como previsão de séries temporais, tradução automática, geração de texto e análise de linguagem natural, possuindo unidades recorrentes para capturar dependências temporais em sequências.
• Estrutura Recorrente: Especializadas em dados sequenciais e temporais, com unidades recorrentes para capturar dependências temporais. A característica distintiva de uma RNN é a estrutura recorrente, que permite que as informações fluam em laços (loops), permitindo que a rede mantenha uma memória interna. Em cada etapa de tempo, a RNN recebe uma entrada do elemento atual da sequência e também recebe informações da saída do estado interno (memória) da etapa de tempo anterior.
• Célula Recorrente: A célula recorrente é o bloco de construção básico de uma RNN. É responsável por manter o estado interno (memória) da rede e atualizá-lo conforme a sequência é processada. A célula recorrente usa os dados de entrada e o estado anterior para calcular a saída e o novo estado interno.
• Retropropagação ao Longo do Tempo (BPTT - Backpropagation Through Time): O treinamento de uma RNN é feito usando uma técnica chamada retropropagação ao longo do tempo (BPTT). Essa técnica é uma extensão do algoritmo de retropropagação padrão que lida com sequências. O BPTT permite que os gradientes de erro sejam propagados através do tempo, atualizando os pesos da rede para minimizar o erro ao longo de toda a sequência.
• Problema do Gradiente Desvanecente (VGP - Vanishing Gradient Problem): As RNNs podem enfrentar o problema do gradiente desvanecente durante o treinamento. Isso acontece porque, em sequências longas, os gradientes podem diminuir drasticamente à medida que são propagados para etapas de tempo anteriores, tornando difícil atualizar os pesos em camadas distantes do passado. Para resolver esse problema, surgiram variantes das RNNs, como as LSTMs - Long Short-Term Memories (Memórias de Longo Prazo) e as GRUs - Gated Recurrent Units (Unidades Recorrentes Fechadas), que são projetadas para preservar melhor as informações de longo prazo.
• Uso de Memória: Mantêm memória de curto e longo prazo por meio de unidades recorrentes.
• Paralelismo: Restrições de paralelismo devido à natureza sequencial.

Camadas nas CNNs:

• Camada Recorrente (SimpleRNN, LSTM, GRU): As RNNs usam camadas recorrentes para lidar com dados sequenciais. Existem várias variantes, como SimpleRNN (recorrente simples), LSTM (Long Short-Term Memory) e GRU (Gated Recurrent Unit), que lidam de diferentes maneiras com a memória de sequências.
• Camada de Embedding: Essa camada é frequentemente usada para representar palavras ou símbolos em vetores contínuos antes de alimentá-los à rede.
• Camada de Ativação (ReLU, tanh, sigmoid): Funções de ativação não lineares são usadas nas camadas recorrentes para introduzir não linearidade.
• Camada de Máscara (Masking): A camada de máscara é usada para mascarar entradas em sequências com comprimentos variáveis, o que é comum em processamento de linguagem natural.
• Camada de Abandono (Dropout): Para regularização, as camadas de abandono são usadas para evitar overfitting.
• Camada de Saída (Dense): Uma camada densa geralmente é usada para produzir a saída final da rede, como a previsão em séries temporais ou classificação em texto.

Aqui está um exemplo de como as classes de camadas do Keras podem ser usadas em uma arquitetura de CNN:

from keras.models import Sequential
from keras.layers import SimpleRNN, Embedding, Dense

# Crie um modelo de RNN sequencial
modelo = Sequential()

# Adicione uma camada de embedding para representar palavras em vetores contínuos
modelo.add(Embedding(input_dim=1000, output_dim=128, input_length=20))

# Adicione uma camada recorrente SimpleRNN com 64 unidades
modelo.add(SimpleRNN(64, activation='relu'))

# Camada de saída com ativação softmax para classificação
modelo.add(Dense(10, activation='softmax'))

As RNNs têm sido amplamente utilizadas em tarefas de NLP, como tradução automática, geração de texto e análise de sentimento, bem como em outras tarefas que envolvem sequências temporais, como previsão de séries temporais, reconhecimento de fala, entre outras. Com as variantes mais avançadas, como as LSTMs e GRUs, as RNNs são capazes de aprender dependências temporais de longo prazo e lidar com sequências mais extensas e complexas.

As Redes Neurais Generativas (GANs - Generative Adversarial Networks) são uma arquitetura especial de rede neural usada para a geração de dados, como imagens, e têm características únicas em comparação com ANNs, CNNs e RNNs.

Consistem em duas redes neurais, o Gerador e o Discriminador, que competem em um jogo adversarial. O Gerador cria dados sintéticos, enquanto o Discriminador tenta distinguir entre dados reais e sintéticos.

Aspectos mencionados em relação às GANs:

• Estrutura: Duas redes neurais, uma com o Gerador e a outra com o Discriminador, que competem em um jogo adversarial.
• Aplicação Principal: A principal aplicação das GANs é a geração de dados realistas. Isso inclui a geração de imagens, vídeos, áudio e muito mais. GANs também são usadas em tarefas de super-resolução, tradução de estilo e geração de conteúdo.
• Convolução vs. Recorrência: As GANs podem incorporar camadas de convolução em seu Gerador e Discriminador, semelhantes às CNNs, para processar dados de imagem. No entanto, GANs não são voltadas para lidar com sequências temporais, como as RNNs.
• Uso de Memória: As GANs não possuem memória de longo prazo como as RNNs. No entanto, elas têm memória de curto prazo durante o treinamento para ajustar o modelo com base nas atualizações do Discriminador.
• Paralelismo: O treinamento de GANs pode ser paralelizado, mas é frequentemente demorado. Treinar GANs profundas pode ser computacionalmente intensivo, requerendo recursos de hardware significativos.
• Gradiente: As GANs também podem enfrentar problemas de gradiente, como desaparecimento ou explosão de gradiente, especialmente em redes profundas. Isso pode afetar a convergência e a qualidade da geração.
• Aprendizado de Características: As GANs realizam aprendizado de características de maneira única. O Gerador aprende a criar características sintéticas que enganam o Discriminador, enquanto o Discriminador aprende a distinguir características realistas das sintéticas. Esse processo iterativo resulta no aprendizado de características relevantes para a geração de dados.

As GANs são uma arquitetura especializada para a geração de dados realistas, envolvendo uma competição adversarial entre o Gerador e o Discriminador. Elas podem incorporar elementos de CNNs para processamento de imagem, mas não são projetadas para lidar com sequências temporais.

O treinamento de GANs pode ser desafiador e requer atenção especial aos problemas de gradiente. Seu foco principal é o aprendizado de características para a geração de dados, resultando em aplicações emocionantes em áreas como visão computacional e geração de conteúdo.

Os neurônios em cada camada são responsáveis por aprender representações dos dados e transmitir essas representações às camadas subsequentes.

O número de neurônios em cada camada de uma rede neural é uma parte fundamental do projeto da rede e tem um impacto significativo no seu desempenho e capacidade de aprendizado, afetando a capacidade da rede de aprender representações complexas dos dados.

Camadas com mais neurônios podem aprender representações mais ricas, mas também podem aumentar a complexidade do modelo.

É importante ajustar esse hiperparâmetro com base na natureza da tarefa e na quantidade de dados disponíveis para o treinamento. Experimentar diferentes tamanhos de camada pode ser necessário para encontrar a configuração ideal para um problema específico.

Vamos explorar como isso funciona.

Número de Neurônios em uma Camada

O número de neurônios em uma camada é também chamado de "tamanho" ou "largura" da camada. É uma das principais decisões de hiperparâmetros ao projetar uma rede neural.

O número de neurônios em uma camada pode variar de acordo com a tarefa. Em geral, uma camada com mais neurônios é capaz de aprender representações mais complexas, mas também pode levar a um aumento na complexidade do modelo e na necessidade de mais dados de treinamento.

Função de Ativação

Cada neurônio em uma camada é associado a uma função de ativação, que determina como o neurônio responde a entradas. Funções comuns incluem ReLU (Unidade Linear Retificada), sigmoid e tangente hiperbólica.

Passagem de Informações

Durante o treinamento, as informações fluem da camada de entrada para as camadas ocultas e, finalmente, para a camada de saída. A passagem de informações ocorre da seguinte maneira:

As entradas são multiplicadas pelos pesos sinápticos associados a cada neurônio na camada.

Os resultados são somados e, em seguida, a função de ativação é aplicada a essa soma para produzir a saída do neurônio.

As saídas dos neurônios em uma camada se tornam as entradas para a camada seguinte. Esse processo de propagação de informações é repetido em todas as camadas da rede até a camada de saída.

Camadas Ocultas e Representações de Características

As camadas intermediárias, chamadas camadas ocultas, são responsáveis por aprender representações intermediárias dos dados. Quanto mais camadas ocultas a rede possui, mais níveis de abstração ela pode aprender.

O número de neurônios em cada camada oculta determina a dimensionalidade dessas representações intermediárias. Camadas com mais neurônios podem aprender representações mais ricas, enquanto camadas com menos neurônios podem aprender representações mais simples.

Aprendizado

Durante o treinamento, a rede ajusta os pesos sinápticos (parâmetros) de cada neurônio para minimizar a função de perda. Isso envolve a propagação do erro retroativamente, ou seja, a retropropagação, para ajustar os pesos em todas as camadas.

Os gradientes se referem às derivadas parciais de uma função de perda em relação aos parâmetros do modelo. Essas derivadas indicam como a função de perda muda à medida que os parâmetros do modelo são ajustados, e são fundamentais para o processo de treinamento de redes neurais.

Para entender melhor o papel dos gradientes no Aprendizado Profundo, aqui estão alguns pontos-chave:

• Função de Perda (Loss Function): A função de perda é uma métrica que quantifica o quão bem o modelo está executando a tarefa. Ela fornece um valor que desejamos minimizar durante o treinamento.
• Gradiente Descendente (Gradient Descent): A otimização no treinamento de redes neurais geralmente envolve a minimização da função de perda. O Gradiente Descendente é um algoritmo utilizado para encontrar os valores dos parâmetros do modelo que minimizam a função de perda.
• Retropropagação de Gradientes: Durante o treinamento, os gradientes são calculados usando a técnica de retropropagação (backpropagation). O processo envolve o cálculo das derivadas parciais da função de perda em relação a todos os parâmetros do modelo. Esses gradientes indicam a inclinação da função de perda em relação a cada parâmetro.
• Atualização dos Parâmetros: Os gradientes são usados para atualizar os parâmetros do modelo em cada iteração do treinamento. A ideia é ajustar os parâmetros na direção em que a função de perda está diminuindo mais rapidamente, o que leva o modelo a um ponto de mínimo da função de perda.
• Taxa de Aprendizado (Learning Rate): A taxa de aprendizado é um hiperparâmetro importante que controla o tamanho dos passos de atualização dos parâmetros com base nos gradientes. Uma taxa de aprendizado adequada é crucial, pois uma taxa muito alta pode fazer com que o treinamento seja instável, e uma taxa muito baixa pode tornar o treinamento demorado ou resultar em convergência para mínimos locais.
• Mínimos Locais e Globais: É importante observar que a otimização com base em gradientes pode levar a mínimos locais em vez de mínimos globais na função de perda. No entanto, na prática, redes neurais profundas frequentemente conseguem bons resultados, mesmo em mínimos locais.

Os gradientes desempenham um papel essencial no treinamento de redes neurais. Eles guiam o processo de ajuste dos parâmetros do modelo para minimizar a função de perda, permitindo que a rede aprenda a fazer previsões precisas em tarefas de aprendizado supervisionado.

O retropropagação (backpropagation) é um algoritmo fundamental para o treinamento de redes neurais artificiais, especialmente em modelos de aprendizado supervisionado. Ele é usado para calcular os gradientes dos pesos da rede em relação à função de perda, permitindo assim a atualização dos pesos durante o processo de treinamento.

A ideia central da retropropagação é realizar uma propagação do erro da saída da rede para as camadas anteriores, calculando os gradientes das funções de ativação em relação aos pesos.

Esse processo acontece em duas fases: a fase de passagem direta (forward pass) e a fase de passagem reversa (backward pass).

• Fase de Passagem Direta (Forward Pass): Durante a passagem direta, os dados de entrada são alimentados na rede, e a saída do modelo é calculada. Cada camada da rede realiza uma combinação linear das entradas ponderadas pelos pesos, seguida pela aplicação de uma função de ativação não linear. Essa sequência de operações é realizada camada por camada, até que a saída final seja produzida.
• Fase de Passagem Reversa (Backward Pass): Após calcular a saída da rede durante a passagem direta (forward pass), o algoritmo de retropropagação inicia a fase de passagem reversa, onde o erro entre a saída prevista e o valor real (rótulo) é propagado para trás na rede. Para calcular os gradientes dos pesos, o algoritmo utiliza a regra da cadeia da derivada, que permite calcular o gradiente de uma função composta em relação a uma variável específica. Os gradientes são calculados recursivamente, começando pela camada de saída e avançando em direção à camada de entrada.
• Atualização dos Pesos: Após calcular os gradientes dos pesos em relação à função de perda, o algoritmo utiliza um otimizador, como o gradiente descendente ou suas variantes, para atualizar os pesos da rede, com o objetivo de minimizar a função de perda. O processo de atualização dos pesos é repetido em cada iteração do treinamento (episódios) até que a rede alcance um bom desempenho na tarefa.

O retropropagação é essencial para o treinamento de redes neurais profundas, onde há várias camadas ocultas, pois permite que a informação do erro seja propagada eficientemente através da rede, ajustando os pesos para que o modelo possa aprender a representar os padrões e relacionamentos presentes nos dados de treinamento.

É importante mencionar que o sucesso da retropropagação está ligado ao uso de funções de ativação não lineares nas camadas ocultas da rede. Sem as funções não lineares, a rede seria apenas uma combinação linear de operações, tornando-a incapaz de aprender representações complexas e abstratas dos dados.

O Aprendizado de Características (FL - Features Learning) é uma etapa essencial em tarefas de ML e DL, agindo no processo de identificar e criar representações ou características significativas e informativas a partir dos dados brutos, tornando-os mais adequados para a tarefa específica em questão.

As características são representações que descrevem diferentes aspectos dos dados, e a qualidade dessas características pode ter um grande impacto no desempenho dos modelos de ML. Quando as características são bem escolhidas e representam de forma eficiente as informações importantes nos dados, os modelos tendem a ter um desempenho melhor e mais robusto.

Existem duas abordagens principais para o FL:

• Extração Manual de Características: Nesta abordagem, as características são projetadas e selecionadas manualmente pelos engenheiros de dados ou especialistas no domínio do problema. Isso requer um conhecimento profundo do domínio e do problema específico, para que as características escolhidas sejam relevantes e informativas. Embora essa abordagem permita maior controle sobre as características, ela também pode ser trabalhosa e limitada pela capacidade humana de identificar todas as informações importantes nos dados.
• Aprendizado Automático de Características: Nesta abordagem, as características são aprendidas automaticamente pelo modelo durante o treinamento. Em vez de depender de características pré-definidas, o modelo é projetado para aprender representações mais úteis e significativas diretamente dos dados brutos. Essa abordagem é especialmente poderosa quando usada com Redes Neurais Artificiais e outras técnicas de DL, onde várias camadas ocultas podem aprender gradualmente representações mais abstratas e complexas dos dados. Essa capacidade de aprendizado automático de características tem sido um dos principais impulsionadores do sucesso do DL em várias tarefas, como visão computacional, NLP e reconhecimento de padrões em geral.

O FL é uma etapa crítica no processo de preparação dos dados para a modelagem de ML e DL. A escolha ou aprendizado de características adequadas pode fazer uma grande diferença no desempenho dos modelos, permitindo que eles capturem com eficácia os padrões e informações importantes presentes nos dados e tornando-os mais robustos e eficientes em suas tarefas.

As três arquiteturas de redes neurais - ANNs, CNNs e RNNs - têm a capacidade de realizar FL, embora a maneira como o fazem possa variar:

As ANNs podem realizar FL, mas geralmente dependem da pré-processamento dos dados de entrada. O FL é frequentemente feita antes de alimentar os dados à rede, no estágio de pré-processamento dos dados. Isso pode incluir redimensionamento, normalização, codificação de variáveis categóricas e extração de características antes de alimentar os dados à camada de entrada da rede.

As CNNs são especialmente eficazes em realizar FL diretamente dos dados de imagem. Elas podem aprender automaticamente a extrair características relevantes das imagens, como bordas, texturas e padrões complexos. O FL ocorre nas camadas de convolução e agrupamento (pooling) de uma CNN. As camadas de convolução aplicam filtros para extrair características locais, enquanto as camadas de pooling reduzem a dimensionalidade e mantêm características relevantes.

As RNNs não são tradicionalmente usadas para o FL, mas podem ser usadas para processar sequências de dados e aprender representações temporais. A principal função das RNNs é modelar dependências temporais em sequências. Elas não realizam FL no sentido convencional, mas podem aprender representações de sequências durante o treinamento.

Todas as três arquiteturas podem contribuir para o FL, mas a maneira como o fazem varia. As CNNs são especialmente poderosas na extração automática de características de imagens, enquanto as ANNs geralmente dependem de pré-processamento de dados. As RNNs são mais focadas em modelar dependências temporais em sequências de dados, embora também possam aprender representações de sequências.

A Transferência de Aprendizado (LT - Learning Transfer) é uma técnica essencial em ML e DL que permite aproveitar conhecimentos adquiridos em uma tarefa ou domínio para melhorar o desempenho em outra tarefa ou domínio relacionado. É uma abordagem poderosa que ajuda a economizar tempo e recursos no treinamento de modelos, especialmente quando há limitações de dados disponíveis.

Princípio da LT

O princípio básico da LT é que um modelo que tenha sido treinado para uma tarefa específica pode aprender representações de características gerais que são úteis para outras tarefas relacionadas.

Essas representações gerais são aprendidas nas camadas mais profundas da rede neural, capturando informações abstratas e complexas dos dados.

Etapas da LT

A aplicação da LT geralmente envolve as seguintes etapas:

• Pré-treinamento (Pretraining): Inicialmente, um modelo é pré-treinado em uma grande quantidade de dados em uma tarefa ou domínio de origem, geralmente em um conjunto de dados com uma quantidade significativa de amostras rotulados. O objetivo é aprender representações de características úteis para a tarefa de origem.
• Extração de Características (Feature Extraction): Após o pré-treinamento, a parte da rede neural que contém as camadas profundas é removida e usada como uma ferramenta de extração de características. Essas camadas são capazes de capturar características gerais dos dados que podem ser reutilizadas para outras tarefas.
• Treinamento (Finetuning): Em seguida, a parte da rede neural remanescente é adicionada, formando um novo modelo. Essa parte é chamada de cabeça do modelo e é usada para ajustar as características aprendidas do modelo de origem para a tarefa de destino. O treinamento é feito em um conjunto de dados menor e mais específico, geralmente com menos amostras rotuladas disponíveis.

Vantagens da LT

A LT oferece várias vantagens:

• Economia de Tempo e Recursos: Ao utilizar um modelo pré-treinado em uma tarefa de origem, é possível economizar tempo e recursos no treinamento do modelo para a tarefa de destino.
• Melhor Desempenho: O uso de características aprendidas em tarefas de origem pode melhorar significativamente o desempenho em tarefas de destino, especialmente quando há poucos dados rotulados disponíveis.
• Generalização Melhorada: As características aprendidas em tarefas de origem tendem a capturar informações mais gerais dos dados, o que pode levar a uma melhor generalização para tarefas de destino relacionadas.

Aplicações da LT

A LT tem aplicações em diversas áreas, incluindo:

• Classificação de imagens em diferentes categorias.
• Reconhecimento de fala e processamento de linguagem natural.
• Detecção de objetos em imagens.
• Previsão de séries temporais em domínios relacionados.

E muitas outras tarefas de ML.

A LT é uma técnica poderosa que permite aproveitar o conhecimento adquirido em tarefas de origem para melhorar o desempenho em tarefas de destino relacionadas.

É especialmente útil quando há poucos dados rotulados disponíveis para a tarefa de destino, tornando-se uma estratégia valiosa para o sucesso de muitos projetos de ML e DL.

O Aprendizado Supervisionado (SL - Supervised Learning) é uma das principais categorias de técnicas de ML. Nesse tipo de aprendizado, o modelo é treinado utilizando um conjunto de dados rotulados, ou seja, dados nos quais as saídas desejadas ou rótulos estão disponíveis para cada exemplo de entrada.

O processo de treinamento do modelo envolve ajustar os parâmetros do modelo para que ele seja capaz de mapear corretamente as entradas para as saídas corretas. O objetivo do SL é fazer com que o modelo generalize bem para novos dados não vistos durante o treinamento, sendo capaz de fazer previsões precisas para novas amostras.

Algumas das principais tarefas de SL incluem:

• Classificação: O modelo deve atribuir uma categoria ou classe a cada exemplo de entrada. Por exemplo, classificar e-mails em "spam" ou "não-spam".
• Regressão: O modelo deve prever um valor contínuo com base nos dados de entrada. Por exemplo, prever o preço de uma casa com base em suas características.

O Aprendizado Não Supervisionado (UL - Unsupervised Learning) é outra categoria de técnicas de ML. Nesse tipo de aprendizado, o modelo é treinado em um conjunto de dados não rotulados, ou seja, os rótulos ou saídas desejadas não estão disponíveis para o modelo durante o treinamento.

O objetivo do UL é encontrar padrões e estruturas ocultas nos dados de entrada sem a necessidade de rótulos prévios. Isso pode ser útil para descobrir grupos (clusters) de amostras semelhantes ou para reduzir a dimensionalidade dos dados para visualização ou compressão.

Algumas das principais tarefas de UL incluem:

• Agrupamento (Clustering): O modelo deve agrupar amostras similares em grupos (clusters), onde cada cluster representa um grupo de amostras que compartilham características semelhantes.
• Redução de Dimensionalidade: O modelo deve reduzir a quantidade de recursos ou características dos dados enquanto preserva as informações importantes. Isso é útil para visualizar dados em gráficos de duas ou três dimensões.

É importante ressaltar que, em algumas situações, é possível combinar técnicas de Aprendizado Supervisionado e Não Supervisionado, como na aprendizagem semi-supervisionada, onde uma parte dos dados é rotulada e outra parte não é. O Aprendizado Supervisionado e o Aprendizado Não Supervisionado são complementares e têm aplicações em diversas áreas, permitindo que os modelos aprendam a partir de diferentes tipos de dados e atendam a diferentes objetivos.

Na construção de redes neurais com o Keras, os desenvolvedores têm à disposição dois principais paradigmas de modelagem: Modelos Sequenciais e Modelos Funcionais.

Os Modelos Sequenciais são ideais para tarefas em que a informação flui de maneira linear de uma camada para a próxima, proporcionando uma abordagem simples e direta na construção de redes.

• Fluxo Linear de Camadas: São a escolha ideal quando você tem uma rede neural em que a informação flui de forma linear, passando por uma série de camadas, uma após a outra. Isso é comum em arquiteturas simples e clássicas, como redes feedforward.
• Construção Simples: Crie um modelo sequencial instanciando e adicionando camadas uma após a outra. A ordem em que você adiciona as camadas define a ordem do fluxo de dados na rede.

Aqui está um exemplo de criação de um Modelo Sequencial em Keras:

from keras.models import Sequential
from keras.layers import Dense

modelo = Sequential()
modelo.add(Dense(32, input_shape=(784,)))
modelo.add(Dense(64, activation='relu'))
modelo.add(Dense(10, activation='softmax'))

Neste exemplo, criamos um Modelo Sequencial com três camadas, onde a primeira camada tem 32 unidades, a segunda tem 64 unidades com ativação ReLU e a terceira tem 10 unidades com ativação softmax para classificação.

Por outro lado, Modelos Funcionais oferecem uma flexibilidade excepcional, permitindo a criação de arquiteturas complexas e personalizadas, com múltiplas entradas e saídas, conexões não lineares entre camadas, e compartilhamento de camadas.

• Arquiteturas Complexas e Conexões Não Lineares: Modelos Funcionais são mais flexíveis e adequados para arquiteturas complexas, como redes com múltiplas entradas ou saídas, conexões não lineares entre camadas e compartilhamento de camadas.
• Construção Personalizada: Para criar um Modelo Funcional, você cria instâncias das camadas de forma independente e, em seguida, conecta essas camadas especificando as entradas e saídas desejadas. Isso permite a criação de arquiteturas altamente personalizadas.

Aqui está um exemplo de criação de um Modelo Funcional em Keras:

from keras.layers import Input, Dense
from keras.models import Model

# Definindo as entradas
dados_entrada = Input(shape=(784,))

# Criando camadas e conectando-as
escondido_1 = Dense(32, activation='relu')(dados_entrada)
escondido_2 = Dense(64, activation='relu')(escondido_1)
output = Dense(10, activation='softmax')(escondido_2)

# Criando o modelo
modelo = Model(inputs=dados_entrada, outputs=output)

Neste exemplo, começamos definindo as entradas, criando camadas independentes e conectando-as para construir uma arquitetura personalizada. Isso é útil quando você precisa criar redes mais complexas, como redes siamesas, redes com múltiplas entradas ou saídas, ou qualquer arquitetura não linear.

Ambos os modelos desempenham um papel crucial no desenvolvimento de redes neurais profundas, adaptando-se a uma variedade de tarefas e requisitos de modelagem.

Em resumo, Modelos Sequenciais são ideais para arquiteturas de rede neural com fluxo linear de camadas, enquanto Modelos Funcionais oferecem flexibilidade para criar arquiteturas complexas e personalizadas, com conexões não lineares entre camadas, múltiplas entradas e saídas, entre outros. A escolha entre eles depende da natureza do seu problema e da arquitetura da rede que você deseja construir.

Redes neurais são modelos de aprendizado de máquina fortemente influenciados pela estrutura e funcionamento do cérebro humano. Elas são compostas por camadas de unidades interconectadas, chamadas de neurônios artificiais ou unidades de processamento. Essas redes são projetadas para processar informações e aprender a partir de dados, tornando-as poderosas para uma ampla gama de tarefas de aprendizado de máquina, como classificação, regressão, processamento de linguagem natural e visão computacional.

O funcionamento de uma rede neural envolve a passagem de dados através das camadas, onde cada neurônio realiza cálculos ponderados e aplica funções de ativação. Durante o treinamento, as conexões entre os neurônios, chamadas de pesos, são ajustadas para minimizar o erro entre as previsões do modelo e os dados de treinamento. Esse processo de ajuste de pesos é realizado por algoritmos de otimização, como o gradiente descendente.

Redes neurais podem variar em complexidade, desde simples redes feedforward com uma única camada oculta até arquiteturas profundas com muitas camadas e milhões de neurônios. O sucesso das redes neurais em tarefas complexas é atribuído, em parte, ao seu poder de representação e à capacidade de aprender características relevantes diretamente dos dados.

CNNs

As Redes Neurais Convolucionais (CNNs - Convolutional Neural Networks) são amplamente utilizadas para tarefas de visão computacional, como reconhecimento de imagens, detecção de objetos e segmentação de imagens.

São algoritmos de DL que recebem imagens como entrada, impondo importância às características (features), baseado-se nos pesos (weights) e vieses (biases) definidos pelos aspectos da rede, para que o classificador possa distinguir as imagens.

A arquitetura de uma CNN é baseada nos padrões dos neurônios de um cérebro humano, onde neurônios respondem individualmente à estímulos em uma área específica do campo visual chamada de campo receptor, e um conjunto desses campos interpretam a imagem.

O Keras oferece suporte completo para a criação e treinamento de CNNs.

Aqui estão alguns recursos e camadas específicas do Keras para CNNs:

• Camada Conv2D: Esta camada é usada para realizar convoluções 2D em dados de entrada, como imagens. Você pode especificar o número de filtros, o tamanho do kernel e a função de ativação.
• Camada MaxPooling2D: Essa camada é usada para realizar operações de max pooling 2D para reduzir a dimensionalidade dos mapas de características.
• Camada Flatten: Após as camadas de convolução e pooling, é comum usar uma camada de achatamento (flatten) para transformar os dados em um vetor unidimensional.
• Camada Dense: Você pode adicionar camadas totalmente conectadas (Dense) para realizar a classificação ou regressão com base nas características extraídas pela CNN.
• Camada Dropout: Camadas de dropout reduzem o risco de sobreajuste (overfitting).
• Camada BatchNormalization: Camadas de normalização por lotes estabilizam o treinamento e aceleram a convergência, reduzindo o risco de sobreajuste.
• Camada Activation: Camadas de ativação aplicam funções não lineares, permitindo que a rede modele relações complexas nos dados, como a classificação, regressão, etc, e que a rede seja capaz de aprender a partir de dados, tornando-as poderosas para tarefas de aprendizado, como detecção de objetos, segmentação de imagens, etc, e reduzindo o risco de sobreajuste.
• Transfer Learning: O Keras facilita o uso de modelos pré-treinados para transfer learning. Você pode importar arquiteturas populares, como VGG16, ResNet, Inception, etc., e ajustá-las para suas tarefas específicas.

Redes Neurais Recorrentes

As Redes Neurais Recorrentes (RNNs - Recurrent Neural Networks) são amplamente utilizadas em redes neurais profundas, em tarefas que envolvem dados sequenciais, como séries temporais, processamento de linguagem natural (NLP), classificação e emparelhamento de texto, verificação de rosto, etc.

O Keras suporta RNNs e oferece camadas específicas para trabalhar com sequências.

Alguns recursos relacionados a RNNs no Keras incluem:

• Camada SimpleRNN, LSTM e GRU: O Keras oferece várias camadas de RNN, incluindo SimpleRNN (RNN simples), LSTM (Long Short-Term Memory) e GRU (Gated Recurrent Unit), que podem ser usadas para modelar sequências de dados.
• Bidirectional RNNs: Você pode criar RNNs bidirecionais para capturar informações de contexto em ambas as direções das sequências.
• Embedding Layers: Para tarefas de NLP, o Keras oferece camadas de embedding que podem ser usadas para converter palavras em vetores densos.

Além de CNNs e RNNs, o Keras suporta uma ampla variedade de outras arquiteturas de redes neurais e tipos de modelos, incluindo:

• Redes Generativas Adversariais (GANs): O Keras facilita a criação de GANs para tarefas de geração de imagens e dados.
• Redes Siamesas: O Keras permite a construção de redes siamesas para tarefas de comparação, como verificação de rosto e emparelhamento de texto.
• Redes Residuais (ResNets): O Keras suporta a criação de arquiteturas de rede com blocos residuais para melhorar o treinamento de redes profundas.
• Redes Recorrentes Convolucionais (CRNs): Para tarefas que envolvem dados de séries temporais e sequências de dados, você pode combinar camadas convolucionais e recorrentes em CRNs.

Essas são apenas algumas das arquiteturas de redes neurais que o Keras suporta. A biblioteca é altamente versátil e permite a construção de uma ampla variedade de modelos para diferentes tipos de tarefas de aprendizado de máquina e deep learning.

Camada Conv2

Conv2D é uma camada de convolução bidimensional usada em redes neurais convolucionais (CNNs) para processar dados de imagem e extrair características locais.

Parâmetros

Através dos parâmetros são definidos os números de filtros, o tamanho do filtro e a função de ativação.

• filters: Número de filtros (ou kernels) a serem aplicados na convolução. Cada filtro é uma janela deslizante que percorre a imagem de entrada para extrair características locais. Quanto mais filtros, mais características a camada pode aprender.
• kernel_size: Tamanho dos filtros. É especificado como uma tupla, como (3, 3) para filtros de 3x3. O tamanho do filtro determina a área da imagem que ele analisa.
• strides: O passo com que o filtro se move pela imagem durante a convolução. Um valor de (1, 1) indica que o filtro se move uma posição por vez, enquanto (2, 2) moverá o filtro duas posições por vez.
• padding: Define como lidar com os limites da imagem. Pode ser 'valid' (sem preenchimento) ou 'same' (preenchimento para manter a mesma saída).
• activation: A função de ativação aplicada após a convolução. ReLU (Unidade Linear Retificada) é comumente usada, mas você pode escolher outras funções, como 'sigmoid' ou 'tanh'.

A camada Conv2D realiza uma operação de convolução bidimensional na imagem de entrada.

Passos

Os passos para construir a camada Conv2D são:

• A imagem de entrada é dividida em pequenas regiões, onde cada região tem o mesmo tamanho que o filtro especificado.
• Cada filtro é aplicado a uma dessas regiões. Para cada região, o filtro realiza uma multiplicação elementar entre seus valores e os valores correspondentes na região da imagem de entrada.
• O resultado das multiplicações é somado, produzindo um único valor. Esse valor é colocado em um novo mapa de características na posição correspondente.
• O filtro é movido pela imagem de entrada de acordo com o valor dos strides, e o processo é repetido para criar o mapa de características resultante.

Mapas de Características

Os mapas de características resultantes da convolução sao chamados de maps, e são usados como entrada para outras camadas.

• Uma camada Conv2D cria múltiplos mapas de características.
• Cada mapa de características captura diferentes características locais da imagem.
• Esses mapas de características são usados como entrada para camadas subsequentes na rede neural.
• Após a convolução, a camada Conv2D aplica a função de ativação especificada, como ReLU. Isso introduz não linearidade na camada, permitindo que a rede aprenda representações mais complexas dos dados.

As camadas Conv2D são fundamentais para CNNs, permitindo que a rede detecte bordas, texturas, padrões e recursos mais complexos em imagens, desempenhando um papel crítico na extração de características relevantes e na capacidade da rede de realizar tarefas de visão computacional, como classificação de objetos, detecção de rostos e segmentação de imagens.

Camada MaxPooling2D

A camada MaxPooling2D no Keras é uma camada de pooling bidimensional usada em redes neurais convolucionais (CNNs) para reduzir a dimensionalidade dos mapas de características e, ao mesmo tempo, preservar as características mais proeminentes.

Parâmetros

Através dos parâmetros são definidos o tamanho da janela de pooling, o passo com que a janela de pooling se move e a maneira de lidar com os limites dos mapas de características.

• pool_size: Tamanho da janela de pooling. É especificado como uma tupla, como (2, 2), indicando uma janela de 2x2 que é deslizada pelos mapas de características.
• strides: O passo com que a janela de pooling se move pelos mapas de características. Um valor de (1, 1) indica que a janela se move uma posição por vez, enquanto (2, 2) moverá a janela duas posições por vez.
• padding: Define como lidar com os limites dos mapas de características. Pode ser 'valid' (sem preenchimento) ou 'same' (preenchimento para manter a mesma saída).

Funcionamento

A camada MaxPooling2D realiza uma operação de pooling bidimensional na saída da camada de convolução.

Aqui estão os passos principais:

• A camada MaxPooling2D divide a saída da camada de convolução em pequenas regiões, onde cada região tem o mesmo tamanho que a janela de pooling especificada.
• Para cada região, a camada MaxPooling2D calcula o valor máximo entre todos os valores nessa região. Em outras palavras, ela retém o valor mais alto (máximo) na região.
• O valor máximo calculado para cada região é colocado em um novo mapa de características na posição correspondente.
• A janela de pooling é movida pelos mapas de características de acordo com o valor dos strides, e o processo é repetido para criar o mapa de características resultante.

Redução da Dimensionalidade

O principal objetivo da camada MaxPooling2D é reduzir a dimensionalidade dos mapas de características, diminuindo o número de unidades (neurônios) em cada mapa.

Isso é benéfico por várias razões:

• Reduz a quantidade de cálculos computacionais necessários na rede.
• Diminui o risco de overfitting, pois reduz o número de parâmetros treináveis.
• Ajuda a manter as características mais proeminentes, uma vez que mantém o valor máximo em cada região.

Uso em CNNs

As camadas MaxPooling2D são frequentemente intercaladas com camadas de convolução em CNNs para criar arquiteturas eficazes na extração de características em imagens. Elas ajudam a consolidar as informações relevantes enquanto reduzem a dimensionalidade, o que é fundamental para a tarefa de processamento de imagens.

Em resumo, a camada MaxPooling2D é uma etapa importante em redes convolucionais para reduzir a dimensionalidade e manter as características mais relevantes. Ela desempenha um papel fundamental na eficácia e eficiência das CNNs, permitindo a extração de características e reduzindo o risco de overfitting.

Camada Dense

a camada da classe Dense é uma das mais comuns usadas em redes neurais artificiais, especialmente em redes neurais feedforward, onde cada neurônio ou unidade em uma camada está conectado a cada neurônio na camada subsequente. A camada Dense é uma camada totalmente conectada, o que significa que cada neurônio na camada atual está conectado a todos os neurônios na camada seguinte.

Aqui estão alguns dos principais aspectos da camada Dense:

Neurônios ou Unidades (Units): A camada Dense é definida com um número de neurônios ou unidades. Cada neurônio na camada representa uma unidade computacional que recebe entradas, executa uma combinação linear das entradas ponderadas e aplica uma função de ativação.

Função de Ativação: Você pode especificar uma função de ativação para os neurônios na camada Dense. Funções de ativação comuns incluem ReLU (Rectified Linear Unit), sigmoid e softmax. A função de ativação determina a saída do neurônio com base na soma ponderada das entradas.

Pesos e Viés (Weights and Bias): Cada conexão entre os neurônios na camada Dense possui um peso. Os pesos são ajustados durante o treinamento da rede para aprender padrões nos dados. Além disso, cada neurônio tem um valor de viés (bias) que é somado à soma ponderada das entradas antes de aplicar a função de ativação.

Operação de Camada Oculta ou de Saída: A camada Dense pode ser usada como uma camada oculta ou como a camada de saída de uma rede neural, dependendo da arquitetura da rede. Em camadas de saída, a função de ativação geralmente é ajustada de acordo com o tipo de problema (por exemplo, softmax para classificação multiclasse).

Flexibilidade na Arquitetura: Você pode adicionar várias camadas Dense em sequência para construir arquiteturas de redes neurais mais complexas. Isso permite que você projete redes com várias camadas e tamanhos variados de unidades.

Aqui está um exemplo de como criar uma camada Dense em uma rede neural usando Keras:

from tensorflow.keras.layers import Dense

# Cria uma camada Dense com 64 neurônios e função de ativação ReLU
dense_layer = Dense(units=64, activation='relu', input_shape=(input_dim,))

Neste exemplo, estamos criando uma camada Dense com 64 neurônios e função de ativação ReLU.

A entrada da camada é especificada pela dimensão input_dim.

Essa camada pode ser adicionada a um modelo sequencial ou funcional para construir a arquitetura da rede.

A camada Dense é uma parte fundamental na construção de redes neurais e é usada em muitos tipos de arquiteturas, como redes feedforward, redes convolucionais e redes recorrentes.

Ela desempenha um papel crucial no aprendizado e na representação de dados em redes neurais.

Função de Ativação ReLU

A função de ativação ReLU (Rectified Linear Unit) é uma das funções de ativação mais amplamente utilizadas em redes neurais artificiais.

A ReLU é uma função não linear que introduz a não linearidade em uma rede neural, o que a torna capaz de aprender relações complexas nos dados.

Aqui estão algumas características importantes da função de ativação ReLU:

• Definição da Função ReLU: A função ReLU é definida como: ⁡f(x) = max(0,x), onde x é o valor de entrada, e a saída da função ReLU é x se x for maior que zero e zero caso contrário.
• Simplicidade e Eficiência: A função ReLU é uma função simples e eficiente, o que torna-a uma boa função de ativação para muitos tipos de problemas de aprendizado e aprendagem. A simplicidade da função ReLU é uma de suas principais vantagens, por ser computacionalmente eficiente, envolvendo apenas uma operação de ativação simples. Além disso, a derivada da ReLU é fácil de calcular, o que é importante no treinamento de redes neurais usando métodos de otimização baseados em gradiente.
• Solução para o Problema de Gradiente Zero (Vanishing Gradient): A função de ativação ReLU, sendo simples e eficiente, torna-se adequada para muitos tipos de problemas de aprendizado erros de gradiente. A ReLU ajuda a mitigar o problema de gradiente zero que ocorre em funções de ativação como a sigmoid e a tangente hiperbólica. O gradiente da ReLU é zero para valores negativos, mas é 1 para valores positivos. Isso permite que o gradiente flua livremente durante o treinamento, ajudando a evitar o desaparecimento do gradiente.
• Esparcidade (Sparsity): A ReLU introduz uma característica interessante chamada esparcidade, onde apenas um subconjunto de neurônios está ativo, o que pode ser útil para a eficiência do modelo. Neurônios que têm valores negativos de entrada produzem uma saída zero. Isso pode resultar em uma representação esparsa, onde apenas um subconjunto de neurônios é ativado, o que pode ser útil para a eficiência do modelo.
• Aplicações Variadas: A ReLU é comumente usada em camadas ocultas de redes neurais. Para tarefas de classificação, regressão e muitas outras, a ReLU tem se mostrado eficaz. No entanto, é importante observar que a ReLU não é apropriada para todas as situações, e existem variações da ReLU, como a Leaky ReLU e a Parametric ReLU, que foram desenvolvidas para abordar suas limitações em algumas situações.
• Limitações: Embora a ReLU seja amplamente utilizada, ela não está isenta de limitações. Um problema conhecido como "dying ReLU" pode ocorrer quando um neurônio permanece inativo (produz saída zero) para todos os exemplos de treinamento. Para lidar com isso, variações da ReLU, como a Leaky ReLU, introduzem pequenos gradientes para valores negativos, evitando que os neurônios morram.

A função de ativação ReLU é uma escolha popular em redes neurais devido à sua simplicidade, eficiência computacional e capacidade de mitigar problemas de gradiente. No entanto, ao usá-la, é importante estar ciente das suas limitações e considerar variações da ReLU, dependendo do problema e das necessidades do modelo.

Função de Ativação Softmax

A função de ativação Softmax é usada comumente em problemas de classificação multiclasse em redes neurais.

Ela converte um vetor de números reais em uma distribuição de probabilidade, onde a soma de todas as saídas é igual a 1.

A função Softmax é fundamental para atribuir probabilidades a cada classe em um problema de classificação, tornando-a uma escolha popular para a camada de saída em muitas arquiteturas de redes neurais.

Aqui estão alguns pontos-chave sobre a função Softmax:

• Definição da Função Softmax: A função Softmax é definida matematicamente como: Softmax(x)i = exp(xi)/∑j=1:K exp(xj), onde x é um vetor de números reais de comprimento K e K é o número de classes. K, e Softmax(x)_i, i é o valor resultante para a i-ésima classe. A função Softmax calcula a exponencial de cada elemento do vetor x, normaliza essas exponenciais pela soma de todas as exponenciais e retorna a probabilidade de cada classe.
• Transformação em Probabilidades: A principal função da função Softmax é transformar as saídas de uma camada anterior (geralmente uma camada densa) em probabilidades. Cada saída representa a probabilidade da amostra pertencer a uma classe específica. Quanto maior o valor resultante, maior a probabilidade.
• Propriedades de Normalização: A função Softmax normaliza as probabilidades de todas as classes para uma probabilidade de 1, garantindo que a soma das probabilidades para todas as classes seja igual a 1. Isso significa que ela produz uma distribuição de probabilidade válida, facilitando a interpretação das previsões do modelo.
• Classificação Multiclasse: A função Softmax é mais frequentemente usada em problemas de classificação multiclasse, onde há mais de duas classes para prever. Cada classe recebe uma probabilidade associada, e a classe com a maior probabilidade é a classe final prevista.
• Função de Perda Cruzada Categórica (Categorical Cross-Entropy): A função Softmax é frequentemente combinada com a função de perda cruzada categórica (categorical cross-entropy) para treinar modelos de classificação multiclasse. A função de perda mede a diferença entre as probabilidades previstas e as probabilidades reais, incentivando o modelo a aprender a atribuir probabilidades corretas às classes.
• Limitações da Função Softmax: A função Softmax é uma função de ativação simples e eficiente, o que torna-a uma boa função de ativação para muitos tipos de problemas de classificação multiclasse, uma escolha natural para problemas de classificação multiclasse, mas pode ser sensível a desequilíbrios de classes. Em situações em que as classes não estão igualmente representadas, pode ser útil explorar outras funções de ativação ou técnicas de treinamento, como a ponderação de classes, para melhorar o desempenho do modelo.

A função Softmax desempenha um papel fundamental no aprendizado supervisionado, onde a classificação de dados em várias classes é uma tarefa comum. Ela converte as saídas do modelo em probabilidades que podem ser usadas para tomar decisões sobre a classe prevista. A normalização garantida pela Softmax facilita a interpretação das previsões e a compreensão da confiança do modelo nas suas escolhas.

Camada Flatten

Flatten é uma camada especial que é frequentemente usada em CNNs para transformar tensores multidimensionais em um vetor unidimensional. Essa transformação é útil quando você deseja conectar camadas totalmente conectadas (como camadas Dense) a camadas de convolução em sua arquitetura.

Aqui estão os principais pontos relacionados à classe da camada Flatten:

• Declaração simplificada: A camada Flatten não requer muitos argumentos. Geralmente, é declarada sem parâmetros, pois simplesmente realiza a transformação dos dados:
• Não Introduz Parâmetros Treináveis: A camada Flatten não introduz nenhum parâmetro treinável na rede. Ela é uma camada puramente de transformação que não realiza nenhum cálculo complexo.
• Conversão de Dados Multidimensionais em Vetor Unidimensional: A camada Flatten é projetada para lidar com dados multidimensionais, como imagens em formato 2D (por exemplo, 28x28 pixels) ou imagens coloridas em formato 3D (por exemplo, 32x32x3 canais de cores). A camada Flatten converte tensores multidimensionais em um vetor unidimensional. Em outras palavras, ela "achata" a saída das camadas anteriores para criar um único vetor de dados que pode ser alimentado em camadas totalmente conectadas, preservando os valores dos dados, mas alterando sua organização espacial. Por exemplo, se você tem uma imagem 2D de 28 x 28 pixels, a camada Flatten a transformará em um vetor de 784 elementos (28 * 28).
• Uso em CNNs: Nas CNNs, as camadas de convolução e agrupamento (pooling) são responsáveis por extrair características espaciais dos dados de entrada, enquanto as camadas Dense (totalmente conectadas) são responsáveis pela classificação ou regressão final. A camada Flatten atua como uma ponte entre esses dois tipos de camadas, permitindo que as características espaciais sejam processadas pelas camadas totalmente conectadas.
• Uso com Camadas Dense: A camada Flatten é frequentemente usada em redes neurais como uma etapa inicial para converter dados de entrada em um formato que pode ser conectado a camadas densas (ou totalmente conectadas). As camadas densas exigem entradas unidimensionais, e a camada Flatten faz essa transformação.

Aqui está um exemplo de como você pode usar a camada Flatten em uma arquitetura de rede neural usando Keras:

from tensorflow.keras.layers import Flatten

modelo = Sequential()
modelo.add(Flatten(input_shape=(28, 28)))  # Converte uma imagem 28x28 em um vetor 1D de 784 elementos
modelo.add(Dense(128, activation='relu'))  # Camada Dense com 128 neuronios após a camada Flatten

Neste exemplo, a camada Flatten é usada para converter imagens 28x28 em vetores unidimensionais antes de conectar a camada densa.

A camada Flatten é uma etapa comum em redes neurais convolucionais (CNNs), onde é frequentemente usada para transformar os dados da camada de convolução em um formato que pode ser alimentado em camadas densas para a tomada de decisões finais. Ela é uma parte essencial do pré-processamento de dados em redes neurais profundas, permitindo que você trabalhe com uma variedade de formatos de dados de entrada.

from tensorflow.keras.layers import Flatten
camada_achatada = Flatten()

Camada Dropout

A camada Dropout é uma técnica de regularização usada em redes neurais para reduzir o sobreajuste (overfitting).

Age desativando aleatoriamente um subconjunto de unidades (neurônios) em cada passagem durante o treinamento.

Isso evita que as unidades se tornem muito dependentes umas das outras e ajuda a melhorar a generalização do modelo.

O hiperparâmetro-chave é a taxa de dropout, que controla a fração de unidades a serem desativadas em cada passagem.

Por exemplo, uma taxa de dropout de 0,5 significa que metade das unidades é desativada aleatoriamente em cada etapa de treinamento.

from keras.layers import Dropout
modelo.add(Dense(128, activation='relu'))
modelo.add(Dropout(0.5))

Camada BatchNormalization

A camada BatchNormalization é usada para normalizar a ativação de cada neurônio em uma camada, tornando o treinamento da rede mais estável, sendo especialmente útil em redes profundas.

A normalização é realizada em lotes de dados de treinamento, podendo atuar como um regularizador, tornando o modelo mais robusto, ajudando a evitar problemas como gradiente desvanecente (vanishing gradient), e acelerando o treinamento.

É comum adicionar uma camada BatchNormalization após a ativação em camadas densas ou convolucionais.

from keras.layers import BatchNormalization
modelo.add(Dense(128, activation='relu'))
modelo.add(BatchNormalization())

Camada Activation

A camada Activation não é uma camada no sentido tradicional, mas é usada para aplicar funções de ativação aos resultados de camadas anteriores.

As funções de ativação introduzem não-linearidade nas redes neurais, permitindo que elas capturem relações complexas nos dados.

Algumas funções de ativação comuns incluem ReLU (Rectified Linear Unit), Sigmoid, Tanh e Softmax, dependendo do tipo de tarefa e camada.

Por exemplo, a função ReLU é comumente usada em camadas ocultas para introduzir não-linearidade.

from keras.layers import Activation
modelo.add(Dense(128))
modelo.add(Activation('relu'))

Este código primeiro carrega os dados de treinamento e teste do conjunto de dados Reuters.

O conjunto de dados Reuters é um conjunto de dados com aproximadamente 10 mil mensagens de notícias classificadas em 46 categorias diferentes.

O código então normaliza os dados dividindo cada caractere por 255. Em seguida, o código cria um modelo de rede neural.

Este modelo é uma rede neural simples com duas camadas ocultas, cada uma com 128 neurônios.

A camada de saída tem 10 neurônios, um para cada classe no conjunto de dados. O código então compila o modelo, definindo o otimizador, a função de perda e as métricas.

Em seguida, o código treina o modelo, alimentando os dados de treinamento.

Por fim, o código avalia o desempenho do modelo, alimentando os dados de teste.

O código imprime a acurácia do modelo, que é a porcentagem de mensagens de notícias que o modelo classificou corretamente.

import numpy as np # álgebra linear
import pandas as pd # processamento de dados, CSV
from keras.datasets import reuters # conjuntos de dados e alvos

Carregar e dividir os dados de treinamento e teste.

(dados_treino, alvos_treino), (dados_teste, alvos_teste) = reuters.load_data(num_words=10000)

Usando o backend TensorFlow.

Dê uma olhada nos dados.

Conjuntos de dados e alvos de treino.

Dados de treino:

print('*** Dados do conjunto de treino')
print(f'Dimensões: {dados_treino.shape}')
print()
print(dados_treino)

*** Dados do conjunto de treino
Dimensões: (8982,)

[list([1, 2, 2, 8, 43, 10, 447, 5, 25, 207, 270, 5, 3095, 111, 16, 369, 186, 90, 67, 7, 89, 5, 19, 102, 6, 19, 124, 15, 90, 67, 84, 22, 482, 26, 7, 48, 4, 49, 8, 864, 39, 209, 154, 6, 151, 6, 83, 11, 15, 22, 155, 11, 15, 7, 48, 9, 4579, 1005, 504, 6, 258, 6, 272, 11, 15, 22, 134, 44, 11, 15, 16, 8, 197, 1245, 90, 67, 52, 29, 209, 30, 32, 132, 6, 109, 15, 17, 12])
 list([1, 3267, 699, 3434, 2295, 56, 2, 7511, 9, 56, 3906, 1073, 81, 5, 1198, 57, 366, 737, 132, 20, 4093, 7, 2, 49, 2295, 2, 1037, 3267, 699, 3434, 8, 7, 10, 241, 16, 855, 129, 231, 783, 5, 4, 587, 2295, 2, 2, 775, 7, 48, 34, 191, 44, 35, 1795, 505, 17, 12])
 list([1, 53, 12, 284, 15, 14, 272, 26, 53, 959, 32, 818, 15, 14, 272, 26, 39, 684, 70, 11, 14, 12, 3886, 18, 180, 183, 187, 70, 11, 14, 102, 32, 11, 29, 53, 44, 704, 15, 14, 19, 758, 15, 53, 959, 47, 1013, 15, 14, 19, 132, 15, 39, 965, 32, 11, 14, 147, 72, 11, 180, 183, 187, 44, 11, 14, 102, 19, 11, 123, 186, 90, 67, 960, 4, 78, 13, 68, 467, 511, 110, 59, 89, 90, 67, 1390, 55, 2678, 92, 617, 80, 1274, 46, 905, 220, 13, 4, 346, 48, 235, 629, 5, 211, 5, 1118, 7, 2, 81, 5, 187, 11, 15, 9, 1709, 201, 5, 47, 3615, 18, 478, 4514, 5, 1118, 7, 232, 2, 71, 5, 160, 63, 11, 9, 2, 81, 5, 102, 59, 11, 17, 12])
 ...
 list([1, 141, 3890, 387, 81, 8, 16, 1629, 10, 340, 1241, 850, 31, 56, 3890, 691, 9, 1241, 71, 9, 5985, 2, 2, 699, 2, 2, 2, 699, 244, 5945, 4, 49, 8, 4, 656, 850, 33, 2993, 9, 2139, 340, 3371, 1493, 9, 2, 22, 2, 1094, 687, 83, 35, 15, 257, 6, 57, 9190, 7, 4, 5956, 654, 5, 2, 6191, 1371, 4, 49, 8, 16, 369, 646, 6, 1076, 7, 124, 407, 17, 12])
 list([1, 53, 46, 957, 26, 14, 74, 132, 26, 39, 46, 258, 3614, 18, 14, 74, 134, 5131, 18, 88, 2321, 72, 11, 14, 1842, 32, 11, 123, 383, 89, 39, 46, 235, 10, 864, 728, 5, 258, 44, 11, 15, 22, 753, 9, 42, 92, 131, 728, 5, 69, 312, 11, 15, 22, 222, 2, 3237, 383, 48, 39, 74, 235, 10, 864, 276, 5, 61, 32, 11, 15, 21, 4, 211, 5, 126, 1072, 42, 92, 131, 46, 19, 352, 11, 15, 22, 710, 220, 9, 42, 92, 131, 276, 5, 59, 61, 11, 15, 22, 10, 455, 7, 1172, 137, 336, 1325, 6, 1532, 142, 971, 6463, 43, 359, 5, 4, 326, 753, 364, 17, 12])
 list([1, 227, 2406, 91, 2, 125, 2855, 21, 4, 3976, 76, 7, 4, 757, 481, 3976, 790, 5259, 5654, 9, 111, 149, 8, 7, 10, 76, 223, 51, 4, 417, 8, 1047, 91, 6917, 1688, 340, 7, 194, 9411, 6, 1894, 21, 127, 2151, 2394, 1456, 6, 3034, 4, 329, 433, 7, 65, 87, 1127, 10, 8219, 1475, 290, 9, 21, 567, 16, 1926, 24, 4, 76, 209, 30, 4033, 6655, 5654, 8, 4, 60, 8, 4, 966, 308, 40, 2575, 129, 2, 295, 277, 1071, 9, 24, 286, 2114, 234, 222, 9, 4, 906, 3994, 8519, 114, 5758, 1752, 7, 4, 113, 17, 12])]

Alvos de treino:

print('*** Alvos do conjunto de treino')
print(f'Dimensões: {alvos_treino.shape}')
print()
print(alvos_treino)

*** Alvos do conjunto de treino
Dimensões: (8982,)

[ 3  4  3 ... 25  3 25]

Conjuntos de dados e alvos de teste.

Dados de teste:

print('*** Dados do conjunto de teste')
print(f'Dimensões: {dados_teste.shape}')
print()
print(dados_teste)

*** Dados do conjunto de teste
Dimensões: (2246,)

[list([1, 4, 1378, 2025, 9, 697, 4622, 111, 8, 25, 109, 29, 3650, 11, 150, 244, 364, 33, 30, 30, 1398, 333, 6, 2, 159, 9, 1084, 363, 13, 2, 71, 9, 2, 71, 117, 4, 225, 78, 206, 10, 9, 1214, 8, 4, 270, 5, 2, 7, 748, 48, 9, 2, 7, 207, 1451, 966, 1864, 793, 97, 133, 336, 7, 4, 493, 98, 273, 104, 284, 25, 39, 338, 22, 905, 220, 3465, 644, 59, 20, 6, 119, 61, 11, 15, 58, 579, 26, 10, 67, 7, 4, 738, 98, 43, 88, 333, 722, 12, 20, 6, 19, 746, 35, 15, 10, 9, 1214, 855, 129, 783, 21, 4, 2280, 244, 364, 51, 16, 299, 452, 16, 515, 4, 99, 29, 5, 4, 364, 281, 48, 10, 9, 1214, 23, 644, 47, 20, 324, 27, 56, 2, 2, 5, 192, 510, 17, 12])
 list([1, 2768, 283, 122, 7, 4, 89, 544, 463, 29, 798, 748, 40, 85, 306, 28, 19, 59, 11, 82, 84, 22, 10, 1315, 19, 12, 11, 82, 52, 29, 283, 1135, 558, 2, 265, 2, 6607, 8, 6607, 118, 371, 10, 1503, 281, 4, 143, 4811, 760, 50, 2088, 225, 139, 683, 4, 48, 193, 862, 41, 967, 1999, 30, 1086, 36, 8, 28, 602, 19, 32, 11, 82, 5, 4, 89, 544, 463, 41, 30, 6273, 13, 260, 951, 6607, 8, 69, 1749, 18, 82, 41, 30, 306, 3342, 13, 4, 37, 38, 283, 555, 649, 18, 82, 13, 1721, 282, 9, 132, 18, 82, 41, 30, 385, 21, 4, 169, 76, 36, 8, 107, 4, 106, 524, 10, 295, 3825, 2, 2476, 6, 3684, 6940, 4, 1126, 41, 263, 84, 395, 649, 18, 82, 838, 1317, 4, 572, 4, 106, 13, 25, 595, 2445, 40, 85, 7369, 518, 5, 4, 1126, 51, 115, 680, 16, 6, 719, 250, 27, 429, 6607, 8, 6940, 114, 343, 84, 142, 20, 5, 1145, 1538, 4, 65, 494, 474, 27, 69, 445, 11, 1816, 6607, 8, 109, 181, 2768, 2, 62, 1810, 6, 624, 901, 6940, 107, 4, 1126, 34, 524, 4, 6940, 1126, 41, 447, 7, 1427, 13, 69, 251, 18, 872, 876, 1539, 468, 9063, 242, 5, 646, 27, 1888, 169, 283, 87, 9, 10, 2, 260, 182, 122, 678, 306, 13, 4, 99, 216, 7, 89, 544, 64, 85, 2333, 6, 195, 7254, 6337, 268, 609, 4, 195, 41, 1017, 2765, 2, 4, 73, 706, 2, 92, 4, 91, 3917, 36, 8, 51, 144, 23, 1858, 129, 564, 13, 269, 678, 115, 55, 866, 189, 814, 604, 838, 117, 380, 595, 951, 320, 4, 398, 57, 2233, 7411, 269, 274, 87, 6607, 8, 787, 283, 34, 596, 661, 5467, 13, 2362, 1816, 90, 2, 84, 22, 2202, 1816, 54, 748, 6607, 8, 87, 62, 6154, 84, 161, 5, 1208, 480, 4, 2, 416, 6, 538, 122, 115, 55, 129, 1104, 1445, 345, 389, 31, 4, 169, 76, 36, 8, 787, 398, 7, 4, 2, 1507, 64, 8862, 22, 125, 2, 9, 2876, 172, 399, 9, 2, 5206, 9, 2, 122, 36, 8, 6642, 172, 247, 100, 97, 6940, 34, 75, 477, 541, 4, 283, 182, 4, 2, 295, 301, 2, 125, 2, 6607, 8, 77, 57, 445, 283, 1998, 217, 31, 380, 704, 51, 77, 2, 509, 5, 476, 9, 2876, 122, 115, 853, 6, 1061, 52, 10, 2, 2, 1308, 5, 4, 283, 182, 36, 8, 5296, 114, 30, 531, 6, 6376, 9, 2470, 529, 13, 2, 2, 58, 529, 7, 2148, 2, 185, 1028, 240, 5296, 1028, 949, 657, 57, 6, 1046, 283, 36, 8, 6607, 8, 4, 2217, 34, 9177, 13, 10, 4910, 5, 4, 141, 283, 120, 50, 2877, 7, 1049, 43, 10, 181, 283, 734, 115, 55, 3356, 476, 6, 2195, 10, 73, 120, 50, 41, 6877, 169, 87, 6607, 8, 107, 144, 23, 129, 120, 169, 87, 33, 2409, 30, 1888, 1171, 161, 4, 294, 517, 23, 2, 25, 398, 9, 2060, 283, 21, 4, 236, 36, 8, 143, 169, 87, 641, 1569, 28, 69, 61, 376, 514, 90, 1249, 62, 2, 13, 4, 2217, 696, 122, 404, 2936, 22, 134, 6, 187, 514, 10, 1249, 107, 4, 96, 1043, 1569, 13, 10, 184, 28, 61, 376, 514, 268, 680, 4, 320, 6, 154, 6, 69, 160, 514, 10, 1249, 27, 4, 153, 5, 52, 29, 36, 8, 6607, 8, 612, 408, 10, 3133, 283, 76, 27, 1504, 31, 169, 951, 2, 122, 36, 8, 283, 236, 62, 641, 84, 618, 2, 22, 8417, 8409, 9, 274, 7322, 399, 7587, 51, 115, 55, 45, 4044, 31, 4, 490, 558, 36, 8, 224, 2, 115, 57, 85, 1655, 2671, 5, 283, 6, 4, 37, 38, 7, 1797, 185, 77, 4446, 4, 555, 298, 77, 240, 2, 7, 327, 652, 194, 8773, 6233, 34, 2, 5463, 4884, 1297, 6, 240, 260, 458, 87, 6, 134, 514, 10, 1249, 22, 196, 514, 4, 37, 38, 309, 213, 54, 207, 8577, 25, 134, 139, 89, 283, 494, 555, 22, 4, 2217, 6, 2172, 4278, 434, 835, 22, 3598, 3746, 434, 835, 7, 48, 6607, 8, 618, 225, 586, 333, 122, 572, 126, 2768, 1998, 62, 133, 6, 2458, 233, 28, 602, 188, 5, 4, 704, 1998, 62, 45, 885, 281, 4, 48, 193, 760, 36, 8, 115, 680, 78, 58, 109, 95, 6, 1732, 1516, 281, 4, 225, 760, 17, 12])
 list([1, 4, 309, 2276, 4759, 5, 2015, 403, 1920, 33, 1575, 1627, 1173, 87, 13, 536, 78, 6490, 399, 7, 2068, 212, 10, 634, 179, 8, 137, 5602, 7, 2775, 33, 30, 1015, 43, 33, 5602, 50, 489, 4, 403, 6, 96, 399, 7, 1953, 3587, 8427, 6603, 4132, 3669, 8180, 7163, 9, 2015, 8, 2, 2, 1683, 791, 5, 740, 220, 707, 13, 4, 634, 634, 54, 1405, 6331, 4, 361, 182, 24, 511, 972, 137, 403, 1920, 529, 6, 96, 3711, 399, 41, 30, 2776, 21, 10, 8491, 2002, 503, 5, 188, 6, 353, 26, 2474, 21, 432, 4, 4234, 23, 3288, 435, 34, 737, 6, 246, 7528, 274, 1173, 1627, 87, 13, 399, 992, 27, 274, 403, 87, 2631, 85, 480, 52, 2015, 403, 820, 13, 10, 139, 9, 115, 949, 609, 890, 819, 6, 812, 593, 7, 576, 7, 194, 2329, 216, 2, 8, 2, 8, 634, 33, 768, 2085, 593, 4, 403, 1920, 185, 9, 107, 403, 87, 2, 107, 1635, 410, 4, 682, 189, 161, 1635, 762, 274, 5319, 115, 30, 43, 389, 410, 4, 682, 107, 1635, 762, 456, 36, 8, 184, 4057, 95, 1854, 107, 403, 87, 302, 2, 8, 129, 100, 756, 7, 3288, 96, 298, 55, 370, 731, 866, 189, 115, 949, 9695, 115, 949, 343, 756, 2, 9, 115, 949, 343, 756, 2509, 36, 8, 17, 12])
 ...
 list([1, 1809, 124, 53, 653, 26, 39, 5439, 18, 14, 5893, 18, 155, 177, 53, 544, 26, 39, 19, 5121, 18, 14, 19, 6382, 18, 280, 3882, 11, 14, 3123, 32, 11, 695, 3614, 47, 11, 14, 3615, 63, 11, 430, 3259, 44, 11, 14, 61, 11, 17, 12])
 list([1, 5586, 2, 71, 8, 23, 166, 344, 10, 78, 13, 68, 80, 467, 606, 6, 261, 5, 146, 93, 124, 4, 166, 75, 3603, 2, 5907, 265, 8692, 1251, 2, 297, 1127, 195, 9, 621, 575, 1080, 5907, 7, 378, 104, 421, 648, 20, 5, 4, 49, 2, 8, 1708, 28, 4, 303, 163, 524, 10, 1220, 6, 455, 4, 326, 685, 6, 2, 422, 71, 142, 73, 863, 62, 75, 3603, 6, 4, 326, 166, 2, 34, 1652, 3603, 6, 4, 166, 4, 49, 8, 17, 12])
 list([1, 706, 209, 658, 4, 37, 38, 309, 484, 4, 1434, 6, 933, 4, 89, 709, 377, 101, 28, 4, 143, 511, 101, 5, 47, 758, 15, 90, 2388, 7, 809, 6, 444, 2035, 4, 911, 5, 709, 198, 1997, 634, 3644, 3798, 2305, 8, 1486, 6, 674, 480, 10, 990, 309, 4008, 2190, 2305, 1849, 24, 68, 583, 242, 5, 4, 143, 709, 364, 7376, 41, 30, 13, 706, 6, 837, 4, 377, 101, 6, 631, 28, 47, 758, 15, 36, 1413, 107, 4, 377, 101, 62, 47, 758, 15, 634, 114, 713, 888, 1412, 6, 343, 37, 38, 1116, 95, 1136, 269, 43, 1488, 1170, 6, 226, 2, 4, 377, 101, 136, 143, 1032, 4, 89, 709, 377, 101, 1217, 30, 478, 97, 47, 948, 15, 90, 4594, 2, 5853, 41, 30, 13, 706, 6, 455, 4, 465, 474, 6, 837, 634, 6, 2069, 4, 709, 377, 101, 28, 47, 758, 15, 7, 463, 29, 89, 1017, 97, 148, 16, 6, 47, 948, 15, 4, 48, 511, 377, 101, 23, 47, 758, 15, 161, 5, 4, 47, 12, 20, 7424, 7978, 386, 240, 2305, 2634, 24, 10, 181, 1475, 7, 194, 534, 21, 709, 364, 756, 33, 30, 4, 386, 404, 36, 118, 4, 2190, 24, 4, 911, 7, 1116, 23, 24, 4, 37, 38, 377, 101, 1976, 42, 9964, 6, 127, 122, 9, 7609, 1136, 692, 13, 37, 38, 1116, 446, 69, 4, 234, 709, 7614, 1320, 13, 126, 1006, 5, 338, 458, 2305, 8, 4, 1136, 911, 23, 4, 307, 2016, 36, 8, 634, 23, 325, 2863, 4, 820, 9, 129, 2767, 40, 836, 85, 1523, 17, 12])]

Alvos de teste:

print('*** Alvos do conjunto de teste')
print(f'Dimensões: {alvos_teste.shape}')
print()
print(alvos_teste)

*** Alvos do conjunto de teste
Dimensões: (2246,)

[ 3 10  1 ...  3  3 24]

Cada exemplo é uma lista de inteiros (índices de palavras).

Podemos transformá-lo novamente em palavras usando o método get_word_index(), que retorna um dicionário de palavras e seus respectivos índices.

No exemplo a seguir a variável indice_palavra é um dicionário de palavras e seus respectivos índices.

indice_palavra = reuters.get_word_index()
print("*** Tamanho dicionário de palavras/índices:", len(indice_palavra))
print(list(índice_palavra.items())[:10]) # 10 primeiros elementos

A variável indice_palavra_reversa é um dicionário de índices e as respectivas palavras, criado a partir da inversão das colunas palavra/indice dos itens de em indice_palavra para indice/palavra nos itens de indice_palavra_reversa.

indice_palavra_reversa = dict([(valor,chave) for (chave, valor) in indice_palavra.items()])
print(list(indice_palavra_reversa.items())[-10:]) # 10 primeiros elementos

Os valores numéricos utilizados em dados_treino podem assim ser usados para representar palavras, encontradas no dicionário da variável indice_palavra_reversa.

noticias_decodificadas = ' '.join([indice_palavra_reversa.get(i - 3, '?') for i in dados_treino[0]])
print(noticias_decodificadas)

? ? ? said as a result of its december acquisition of space co it expects earnings per share in 1987 of 1 15 to 1 30 dlrs per share up from 70 cts in 1986 the company said pretax net should rise to nine to 10 mln dlrs from six mln dlrs in 1986 and rental operation revenues to 19 to 22 mln dlrs from 12 5 mln dlrs it said cash flow per share this year should be 2 50 to three dlrs reuter 3

O rótulo associado a um exemplo é um número inteiro entre 0 e 45 (índice de tópico).

Preparando os dados

Vamos vetorizar os dados de treinamento usando o tensor inteiro e o train_label usando a codificação one-hot.

A codificação one-hot (one-hot encoding), também chamada de codificação categórica, é um formato amplamente utilizado para dados categóricos.

def vetorizar_sequencias(sequencias, dimension=10000):
    resultados = np.zeros((len(sequencias),dimension))
    for i,sequencia in enumerate(sequencias):
        resultados[i,sequencia] = 1
    return resultados

dados_treino = vetorizar_sequencias(dados_treino)
dados_teste = vetorizar_sequencias(dados_teste)

print('*** Amostra de dados de treino:')
print(dados_treino[0])

print()

print('*** Amostra de dados de teste:')
print(dados_teste[0])

*** Amostra de dados de treino:
[0. 1. 1. ... 0. 0. 0.]

*** Amostra de dados de teste:
[0. 1. 1. ... 0. 0. 0.]

Função to_categorical() integrada com a codificação one-hot

from keras.utils import to_categorical

rotulos_treino_one_hot = to_categorical(alvos_treino)
rotulos_teste_one_hot = to_categorical(alvos_teste)

print(f'uma amostra de rótulos one-hot: {rotulos_treino_one_hot[0]}')

uma amostra de rótulos one-hot: [0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]

Construindo a rede

Na construção das pilhas de camadas Dense, cada camada só pode acessar as informações da saída da camada anterior.

Se uma das camadas deixar "cair" alguma informação sobre a classificação, cada camada poderá se tornar um gargalo de informações.

É por isso que usaremos camadas maiores.

from keras import models
from keras import layers

modelo = models.Sequential()
modelo.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
modelo.add(layers.Dense(64, activation='relu'))
modelo.add(layers.Dense(46, activation='softmax'))

modelo.compile(
    optimizer='rmsprop',
    loss='categorical_crossentropy',
    metrics=['accuracy'])

Validando nossa abordagem

Vamos dividir dados_treino em dados_treino_parciais e valores_dados.

Vamos colocar 1000 amostras de dados_treino em valores_dados.

valores_dados = dados_treino[:1000]
dados_treino_parciais = dados_treino[1000:]

valores_alvos = rotulos_treino_one_hot[:1000]
alvos_treino_parciais = rotulos_treino_one_hot[1000:]

history = modelo.fit(
    dados_treino_parciais,
    alvos_treino_parciais,
    epochs=20,
    batch_size=512,
    validation_data=(valores_dados,valores_alvos))

Plotando a perda de treinamento e validação

import matplotlib.pyplot as plt

perdas = history.history['loss']
valores_perda = history.history['val_loss']

episodios = range(1,len(perdas) + 1)

plt.clf()
plt.plot(episodios, perdas, 'r', label='Perdas de treinamento')
plt.plot(episodios, valores_perda, 'b', label='Perdas de validação')
plt.title('Perda de treinamento versus perda de validação')
plt.xlabel('Episódios')
plt.ylabel('Perdas')
plt.legend()
plt.show()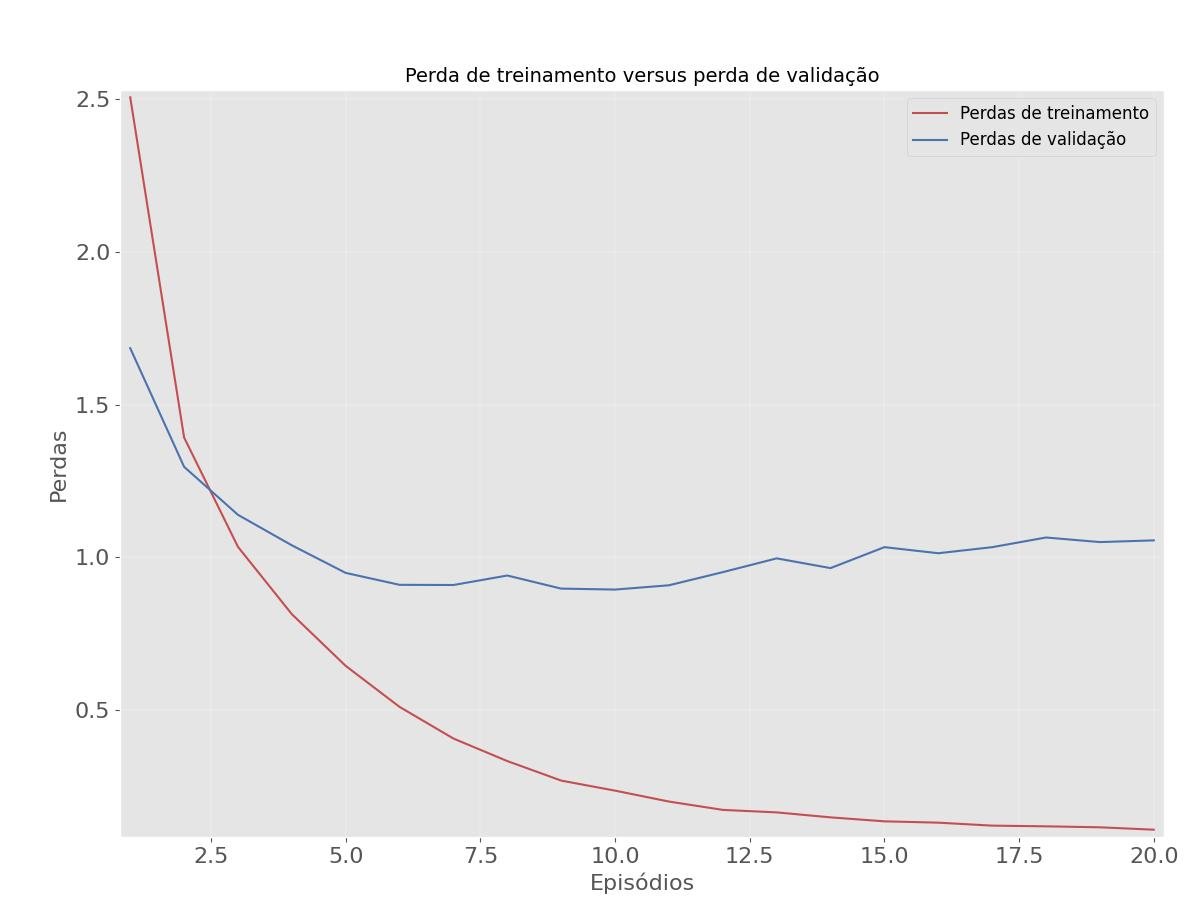

Traçando a precisão do treinamento e da validação.

acc = history.history['accuracy']
val_acc = history.history['val_accuracy']
plt.clf()
plt.plot(episodios, acc, 'r', label='Acurácia do treinamento')
plt.plot(episodios, val_acc, 'b', label='Acurácia de validação')
plt.xlabel('Episódios')
plt.ylabel('Acurácia')
plt.legend()
plt.show()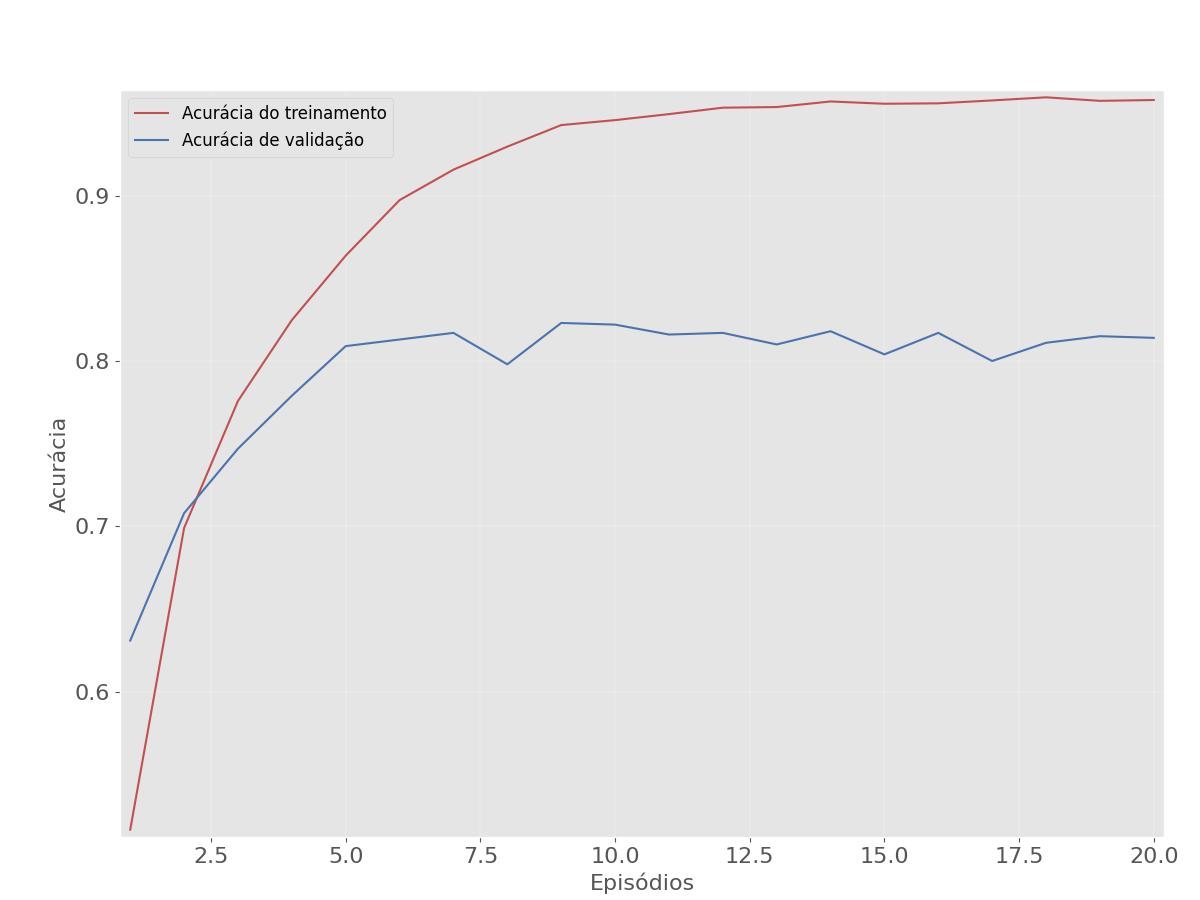

Recalculando:

modelo = models.Sequential()
modelo.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
modelo.add(layers.Dense(64, activation='relu'))
modelo.add(layers.Dense(46, activation='softmax'))

modelo.compile(
    optimizer='rmsprop',
    loss='categorical_crossentropy',
    metrics=['accuracy'])

modelo.fit(dados_treino_parciais,
    alvos_treino_parciais, 
    epochs=9,
    batch_size=512,
    validation_data=(valores_dados,valores_alvos))

Avalie o modelo.

resultados = modelo.evaluate(dados_teste, rotulos_teste_one_hot)

Imprima os resultados.

print(resultados)

[0.979252278804779, 0.7853962779045105]

A perda é uma medida que indica o quão bem o modelo está performando na tarefa.

Neste caso, a perda é relativamente alta, indicando que o modelo está tendo dificuldades em fazer previsões precisas.

Uma perda de aproximadamente 1 é considerada relativamente alta para muitos problemas de classificação.

Isso pode sugerir que o modelo está tendo dificuldades em se ajustar aos dados de treinamento e está cometendo erros significativos.

A acurácia (ou precisão) é uma métrica que expressa a porcentagem de classificações corretas em relação ao total de amostras no conjunto de teste.

No exemplo, a precisão é de cerca de 78%, o que significa que o modelo está classificando corretamente aproximadamente 78% das amostras no conjunto de teste.

A interpretação dos resultados depende do contexto da tarefa e das expectativas de desempenho. Neste caso, os valores sugerem que o modelo não está performando tão bem quanto em alguns outros cenários.

A perda relativamente alta pode indicar problemas com o treinamento do modelo, como sobreajuste (ajuste excessivo, overfitting) ou subajuste (underfitting), que podem ser resolvidos ajustando os hiperparâmetros do modelo.

A precisão de 78% também indica que o modelo está cometendo erros em cerca de 22% das previsões, o que pode ou não ser aceitável, dependendo da natureza da tarefa.

Portanto, seria aconselhável realizar uma análise mais aprofundada do modelo, ajustar hiperparâmetros, explorar diferentes arquiteturas de rede ou realizar outras ações para melhorar o desempenho, caso seja necessário.

Modelo com gargalo de informações

Modelos com camadas intermediárias com menos de 46 unidades ocultas.

modelo = models.Sequential()
modelo.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
modelo.add(layers.Dense(4, activation='relu'))
modelo.add(layers.Dense(46, activation='softmax'))

modelo.compile(optimizer='rmsprop',
            loss='categorical_crossentropy',
            metrics=['accuracy'])

modelo.fit(dados_treino_parciais,
            alvos_treino_parciais,
            epochs=20,
            batch_size=128,
            validation_data=(valores_dados, valores_alvos))

resultados = modelo.evaluate(dados_teste, rotulos_teste_one_hot)

Imprima os resultados.

print(resultados)

[2.2108521461486816, 0.6923419237136841]

Utilizando mais neurônios que o necessário em uma camada Dense.

modelo = models.Sequential()
modelo.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
modelo.add(layers.Dense(128, activation='relu'))
modelo.add(layers.Dense(46, activation='softmax'))

modelo.compile(
    optimizer='rmsprop',
    loss='categorical_crossentropy',
    metrics=['accuracy'])

modelo.fit(
    dados_treino_parciais,
    alvos_treino_parciais,
    epochs=20,
    batch_size=128,
    validation_data=(valores_dados, valores_alvos))

resultados = modelo.evaluate(dados_teste, rotulos_teste_one_hot)

print(resultados)

[1.5290597677230835, 0.7818343639373779]

Com apenas duas camadas Dense.

modelo = models.Sequential()

modelo.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
modelo.add(layers.Dense(46, activation='softmax'))

modelo.compile(
    optimizer='rmsprop',
    loss='categorical_crossentropy',
    metrics=['accuracy'])

modelo.fit(
    dados_treino_parciais,
    alvos_treino_parciais,
    epochs=20,
    batch_size=128,
    validation_data=(valores_dados, valores_alvos))

resultados = modelo.evaluate(dados_teste, rotulos_teste_one_hot)

Imprima os resultados:

print(resultados)

[1.384070873260498, 0.7871772050857544]

Este código primeiro carrega os dados de treinamento e teste do conjunto de dados CIFAR-10, de imagens de 10 classes diferentes: pássaros, gatos, cães, sapos, cavalos, cervos, carros, aviões, navios e caminhões.

Em seguida, o código cria um modelo de rede neural.

Este modelo é uma rede neural simples com duas camadas ocultas, cada uma com 128 neurônios.

A camada de saída tem 10 neurônios, um para cada classe no conjunto de dados.

O código então compila o modelo, definindo o otimizador, a função de perda e as métricas.

Em seguida, o código treina o modelo, alimentando os dados de treinamento.

Por fim, o código avalia o desempenho do modelo, alimentando os dados de teste.

O código então normaliza os dados dividindo cada pixel por 255. Isto é feito para que todos os dados estejam na mesma escala.

O código imprime a acurácia do modelo, que é a porcentagem de imagens que o modelo classificou corretamente.

Importar bibliotecas

import keras
from keras.models import Sequential
from keras.layers import Dense, Flatten
from keras.datasets import cifar10

Carregar os dados

Carrege os dados de treinamento e teste.

(dados_treino, alvos_treino), (dados_teste, alvos_teste) = cifar10.load_data()

Imprima as dimensões dos dados

Visualize os dados.

Primeiro, os conjuntos de dados e alvos de treino.

Dados de treino:

print('*** Dados do conjunto de treino')
print(f'Tipo: {type(dados_treino)}')
print(f'Dims: {dados_treino.shape}')
print()
print(dados_treino)

*** Dados do conjunto de treino
Tipo: <class 'numpy.ndarray'>
Dims: (50000, 32, 32, 3)

[[[[ 59  62  63] [ 43  46  45] [ 50  48  43]
   ...
   [158 132 108] [152 125 102] [148 124 103]]

  [[ 16  20  20] [  0   0   0] [ 18   8   0]
   ...
   [123  88  55] [119  83  50] [122  87  57]]

  [[ 25  24  21] [ 16   7   0] [ 49  27   8]
   ...
   [118  84  50] [120  84  50] [109  73  42]]

  ...

  [[208 170  96] [201 153  34] [198 161  26]
   ...
   [160 133  70] [ 56  31   7] [ 53  34  20]]

  [[180 139  96] [173 123  42] [186 144  30]
   ...
   [184 148  94] [ 97  62  34] [ 83  53  34]]

  [[177 144 116] [168 129  94] [179 142  87]
   ...
   [216 184 140] [151 118  84] [123  92  72]]]


 [[[154 177 187] [126 137 136] [105 104  95]
   ...
   [ 91  95  71] [ 87  90  71] [ 79  81  70]]

  [[140 160 169] [145 153 154] [125 125 118]
   ...
   [ 96  99  78] [ 77  80  62] [ 71  73  61]]

  [[140 155 164] [139 146 149] [115 115 112]
   ...
   [ 79  82  64] [ 68  70  55] [ 67  69  55]]

  ...

  [[175 167 166] [156 154 160] [154 160 170]
   ...
   [ 42  34  36] [ 61  53  57] [ 93  83  91]]

  [[165 154 128] [156 152 130] [159 161 142]
   ...
   [103  93  96] [123 114 120] [131 121 131]]

  [[163 148 120] [158 148 122] [163 156 133]
   ...
   [143 133 139] [143 134 142] [143 133 144]]]


 [[[255 255 255] [253 253 253] [253 253 253]
   ...
   [253 253 253] [253 253 253] [253 253 253]]

  [[255 255 255] [255 255 255] [255 255 255]
   ...
   [255 255 255] [255 255 255] [255 255 255]]

  [[255 255 255] [254 254 254] [254 254 254]
   ...
   [254 254 254] [254 254 254] [254 254 254]]

  ...

  [[113 120 112] [111 118 111] [105 112 106]
   ...
   [ 72  81  80] [ 72  80  79] [ 72  80  79]]

  [[111 118 110] [104 111 104] [ 99 106  98]
   ...
   [ 68  75  73] [ 70  76  75] [ 78  84  82]]

  [[106 113 105] [ 99 106  98] [ 95 102  94]
   ...
   [ 78  85  83] [ 79  85  83] [ 80  86  84]]]

 ...

 [[[ 35 178 235] [ 40 176 239] [ 42 176 241]
   ...
   [ 99 177 219] [ 79 147 197] [ 89 148 189]]

  [[ 57 182 234] [ 44 184 250] [ 50 183 240]
   ...
   [156 182 200] [141 177 206] [116 149 175]]

  [[ 98 197 237] [ 64 189 252] [ 69 192 245]
   ...
   [188 195 206] [119 135 147] [ 61  79  90]]

  ...

  [[ 73  79  77] [ 53  63  68] [ 54  68  80]
   ...
   [ 17  40  64] [ 21  36  51] [ 33  48  49]]

  [[ 61  68  75] [ 55  70  86] [ 57  79 103]
   ...
   [ 24  48  72] [ 17  35  53] [  7  23  32]]

  [[ 44  56  73] [ 46  66  88] [ 49  77 105]
   ...
   [ 27  52  77] [ 21  43  66] [ 12  31  50]]]


 [[[189 211 240] [186 208 236] [185 207 235]
   ...
   [175 195 224] [172 194 222] [169 194 220]]

  [[194 210 239] [191 207 236] [190 206 235]
   ...
   [173 192 220] [171 191 218] [167 190 216]]

  [[208 219 244] [205 216 240] [204 215 239]
   ...
   [175 191 217] [172 190 216] [169 191 215]]

  ...

  [[207 199 181] [203 195 175] [203 196 173]
   ...
   [135 132 127] [162 158 150] [168 163 151]]

  [[198 190 170] [189 181 159] [180 172 147]
   ...
   [178 171 160] [175 169 156] [175 169 154]]

  [[198 189 173] [189 181 162] [178 170 149]
   ...
   [195 184 169] [196 189 171] [195 190 171]]]


 [[[229 229 239] [236 237 247] [234 236 247]
   ...
   [217 219 233] [221 223 234] [222 223 233]]

  [[222 221 229] [239 239 249] [233 234 246]
   ...
   [223 223 236] [227 228 238] [210 211 220]]

  [[213 206 211] [234 232 239] [231 233 244]
   ...
   [220 220 232] [220 219 232] [202 203 215]]

  ...

  [[150 143 135] [140 135 127] [132 127 120]
   ...
   [224 222 218] [230 228 225] [241 241 238]]

  [[137 132 126] [130 127 120] [125 121 115]
   ...
   [181 180 178] [202 201 198] [212 211 207]]

  [[122 119 114] [118 116 110] [120 116 111]
   ...
   [179 177 173] [164 164 162] [163 163 161]]]]

Imprima apenas o primeiro elemento do conjunto de dados, para formar ideia do formato das imagens.

primeiro_dado_treino = dados_treino[0]
print(f'Tipo: {type(primeiro_dado_treino)}')
print(f'Dims: {primeiro_dado_treino.shape}')
print()
print(primeiro_dado_treino)

Tipo: <class 'numpy.ndarray'>
Dims: (32, 32, 3)

[[[ 59  62  63] [ 43  46  45] [ 50  48  43]
  ...
  [158 132 108] [152 125 102] [148 124 103]]

 [[ 16  20  20] [  0   0   0] [ 18   8   0]
  ...
  [123  88  55] [119  83  50] [122  87  57]]

 [[ 25  24  21] [ 16   7   0] [ 49  27   8]
  ...
  [118  84  50] [120  84  50] [109  73  42]]

 ...

 [[208 170  96] [201 153  34] [198 161  26]
  ...
  [160 133  70] [ 56  31   7] [ 53  34  20]]

 [[180 139  96] [173 123  42] [186 144  30]
  ...
  [184 148  94] [ 97  62  34] [ 83  53  34]]

 [[177 144 116] [168 129  94] [179 142  87]
  ...
  [216 184 140] [151 118  84] [123  92  72]]]

Alvos de treino:

Os alvos são um conjunto de números inteiros entre 0 e 9.

print('*** Alvos do conjunto de treino')
print(f'Tipo: {type(alvos_treino)}')
print(f'Dims: {alvos_treino.shape}')
print()
print(alvos_treino)

*** Alvos do conjunto de treino
Tipo: <class 'numpy.ndarray'>
Dims: (50000, 1)

[[6] [9] [9] ... [9] [1] [1]]

Imprima apenas o primeiro elemento do conjunto de alvos, para formar ideia do formato das etiquetas.

primeiro_alvo_treino = alvos_treino[0]
print(f'Tipo: {type(primeiro_alvo_treino)}')
print(f'Dims: {primeiro_alvo_treino.shape}')
print()
print(primeiro_alvo_treino)

*** Alvos do conjunto de treino
Tipo: <class 'numpy.ndarray'>
Dims: (1, )

[6]

O conjunto de dados CIFAR-10 do Keras não fornece métodos integrados para recuperar diretamente os rótulos originais das classes em formato de texto.

No entanto, você pode facilmente criar uma lista de textos com os rótulos das classes com base no conhecimento das classes do conjunto de dados.

Os rótulos das classes no CIFAR-10 são as seguintes:

• 0: Avião
• 1: Automóvel
• 2: Pássaro
• 3: Gato
• 4: Cervo
• 5: Cachorro
• 6: Sapo
• 7: Cavalo
• 8: Navio
• 9: Caminhão

Você pode criar manualmente uma lista de strings correspondente a essas classes da seguinte maneira:

rotulos_classes = [
    "Avião", "Automóvel", "Pássaro", "Gato", "Cervo",
    "Cachorro", "Sapo", "Cavalo", "Navio", "Caminhão"
]

Agora, você pode usar a lista rotulos_classes para mapear os rótulos das classes em formato numérico para os rótulos originais em formato de texto.

Por exemplo, rotulos_classes[0] retorna "Avião", rotulos_classes[1] retorna "Automóvel" e assim por diante.

Esta abordagem é simples e eficaz para associar rótulos originais às classes no conjunto de dados CIFAR-10.

Os conjuntos de dados e alvos de teste são semelhantes aos conjuntos de dados e alvos de treino, com valores diferentes.

Criar o modelo

Crie o modelo Sequential e adicione camadas Flatten, Dense (ReLU) e Dense (Softmax).

modelo = Sequential()
modelo.add(Flatten(input_shape=(32, 32, 3)))
modelo.add(Dense(128, activation='relu'))
modelo.add(Dense(10, activation='softmax'))

Compilar o modelo

Compile o modelo.

modelo.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])

Treinar o modelo

Treine o modelo.

modelo.fit(dados_treino, alvos_treino, epochs=10)

Epoch 1/10
1563/1563 [==============================] - 10s 6ms/step - loss: 9.4726 - accuracy: 0.1012
Epoch 2/10
1563/1563 [==============================] - 9s 6ms/step - loss: 2.3027 - accuracy: 0.0992
Epoch 3/10
1563/1563 [==============================] - 9s 6ms/step - loss: 2.3026 - accuracy: 0.0987
Epoch 4/10
1563/1563 [==============================] - 10s 6ms/step - loss: 2.3027 - accuracy: 0.0994
Epoch 5/10
1563/1563 [==============================] - 9s 6ms/step - loss: 2.3028 - accuracy: 0.0979
Epoch 6/10
1563/1563 [==============================] - 9s 6ms/step - loss: 2.3027 - accuracy: 0.0981
Epoch 7/10
1563/1563 [==============================] - 9s 6ms/step - loss: 2.3028 - accuracy: 0.0993
Epoch 8/10
1563/1563 [==============================] - 10s 6ms/step - loss: 2.3028 - accuracy: 0.0990
Epoch 9/10
1563/1563 [==============================] - 10s 6ms/step - loss: 2.3028 - accuracy: 0.0999
Epoch 10/10
1563/1563 [==============================] - 10s 6ms/step - loss: 2.3028 - accuracy: 0.0975

Durante o treinamento são apresentados os cálculos dos 10 episódios, observe o tempo de treinamento, a perda (loss) e a acurácia (accuracy).

A perda em todos os episódios é alta e a acurácia é baixa, em torno de 0.1 (10%).

Avaliar o modelo

Avalie o desempenho do modelo com os dados de teste.

escore = modelo.evaluate(dados_teste, alvos_teste)

Imprima a acurácia.

print(f'Acurácia: {escore[1]:.4f}')
print(f'Perda: {escore[0]:.4f}')

Acurácia: 0.1000
Perda: 2.3027

A acurância do conjunto de teste é baixa, em torno de 0.1 (10%), a taxa de perda alta, pelo que o modelo está sobreajustado ou subajustado.

Normalizando os dados

Vamos normalizar os dados de entrada para que os dados de entrada sejam valores entre 0 e 1, visando que a rede neural aprenda melhor.

Normalize os dados.

Como os valores de pixels estão entre 0 e 255, dividir os valores de entrada por 255 normalizará os dados de entrada para valores entre 0 (0/255) e 1 (255/255).

dados_treino = dados_treino / 255.0
dados_teste = dados_teste / 255.0

Imprima apenas o primeiro elemento do conjunto de dados de treino normalizado, para formar ideia do formato normalizado das imagens.

print('*** Dados do conjunto de treino')
print(dados_treino[0])

*** Dados do conjunto de treino normalizado
[[[0.23 0.24 0.24] [0.16 0.18 0.17] [0.19 0.18 0.16]
  ...
  [0.61 0.51 0.42] [0.59 0.49 0.4 ] [0.58 0.48 0.40]]

 [[0.06  0.07 0.07] [0.  0.   0.  ] [0.07 0.03 0.  ]
  ...
  [0.48 0.34 0.21] [0.46 0.32 0.19] [0.47 0.34 0.22]]

 [[0.09 0.09 0.08] [0.06 0.02 0.  ] [0.19 0.10 0.03]
  ...
  [0.46 0.32 0.19] [0.47 0.32 0.19] [0.42 0.28 0.16]]

 ...

 [[0.81 0.66 0.37] [0.78 0.6  0.13] [0.77 0.63 0.10]
  ...
  [0.62 0.52 0.27] [0.21 0.12 0.02] [0.20 0.13 0.07]]

 [[0.70 0.54 0.37] [0.67 0.48 0.16] [0.72 0.56 0.11]
  ...
  [0.72 0.58 0.36] [0.38 0.24 0.13] [0.32 0.20 0.13]]

 [[0.69 0.56 0.45] [0.65 0.50 0.36] [0.70 0.55 0.34]
  ...
  [0.84 0.72 0.54] [0.59 0.46 0.32] [0.48 0.36 0.28]]]

Crie o modelo.

modelo = Sequential()
modelo.add(Flatten(input_shape=(32, 32, 3)))
modelo.add(Dense(128, activation='relu'))
modelo.add(Dense(10, activation='softmax'))

Compile o modelo.

modelo.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])

Treine o modelo.

modelo.fit(dados_treino, alvos_treino, epochs=10)

Epoch 1/10
1563/1563 [==============================] - 11s 6ms/step - loss: 1.8943 - accuracy: 0.3264
Epoch 2/10
1563/1563 [==============================] - 9s 6ms/step - loss: 1.7427 - accuracy: 0.3784
Epoch 3/10
1563/1563 [==============================] - 10s 6ms/step - loss: 1.6873 - accuracy: 0.3981
Epoch 4/10
1563/1563 [==============================] - 9s 6ms/step - loss: 1.6514 - accuracy: 0.4114
Epoch 5/10
1563/1563 [==============================] - 9s 6ms/step - loss: 1.6278 - accuracy: 0.4225
Epoch 6/10
1563/1563 [==============================] - 9s 6ms/step - loss: 1.6050 - accuracy: 0.4291
Epoch 7/10
1563/1563 [==============================] - 9s 6ms/step - loss: 1.5846 - accuracy: 0.4364
Epoch 8/10
1563/1563 [==============================] - 9s 6ms/step - loss: 1.5734 - accuracy: 0.4404
Epoch 9/10
1563/1563 [==============================] - 9s 6ms/step - loss: 1.5594 - accuracy: 0.4443
Epoch 10/10
1563/1563 [==============================] - 10s 6ms/step - loss: 1.5526 - accuracy: 0.4467

Observe o desempenho do modelo. Durante o treinamento são apresentados os cálculos dos 10 episódios, observe os valores de perda (loss) e de acurácia (accuracy).

Embora os valores de acurácia e de perda tenham sido significativamente melhores com valores normalizados, em relação aos valores originais, a perda em todos os episódios é alta e a acurácia é baixa, em torno de 0.44 (44%).

Isso significa que o modelo consegue acertar apenas 44% das imagens, menos da metade.

Avalie o desempenho do modelo com os dados de teste.

escore = modelo.evaluate(dados_teste, alvos_teste)

Imprima a acurácia.

print(f'Acurácia: {escore[1]:.4f}')
print(f'Perda: {escore[0]:.4f}')

Acurácia: 0.4307
Perda: 1.6005

A acurância do conjunto de teste normalizado é melhor que a acurácia do conjunto de teste original, sem normalização, em torno de 0.43 (43%), e a perda alta, demonstrando que o modelo está sobre/subajustado.

Este é apenas um exemplo simples de código.

Para obter melhores resultados, você precisará usar um conjunto de dados maior e mais diversificado, treinar seu modelo por mais épocas e usar uma arquitetura de rede neural mais complexa.

No artigo acadêmico An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale, os autores mencionam que os Tranformadores de Visão (ViT - Vision Transformers) são ávidos por dados.

Portanto, pré-treinar um ViT em um conjunto de dados de grande porte como JFT300M e ajustá-lo em conjuntos de dados de tamanho médio (como ImageNet) é a única maneira de superar os modelos de rede neural convolucional de última geração.

JFT-300M é um conjunto de dados interno do Google usado para treinar modelos de classificação de imagens, rotuladas usando-se um algoritmo com uma mistura complexa de sinais brutos da web, conexões entre páginas da web e feedback do usuário, resultando em mais de um bilhão de rótulos para 300 milhões de imagens (uma única imagem pode ter vários rótulos). Dos bilhões de rótulos de imagens, aproximadamente 375 milhões são selecionados por meio de um algoritmo que visa maximizar a precisão dos rótulos das imagens selecionadas.

A camada de autoatenção do ViT carece de viés indutivo de localidade (a noção de que os pixels da imagem são correlacionados localmente e que seus mapas de correlação são invariantes à tradução). Esta é a razão pela qual os ViTs precisam de mais dados. Por outro lado, as CNNs analisam as imagens através de janelas deslizantes espaciais, o que as ajuda a obter melhores resultados com conjuntos de dados menores.

As camadas de autoatenção (self-attention), são componentes fundamentais em arquiteturas de modelos como o Transformador (Transformer) e também são usadas nas Redes Neurais Convolucionais (CNNs) de ViT, desempenhando um papel crucial na extração de informações contextuais dos dados e permitindo que o modelo se concentre em partes relevantes da entrada durante o processamento.

Em um contexto de ViT, essas camadas de autoatenção são particularmente interessantes porque permitem que o modelo lide com imagens de forma eficaz, capturando as relações entre pixels ou correções (patches) de maneira eficaz e permitindo que o modelo aprenda a atenção em patchs de maneira semelhante à sua aplicação em dados sequenciais, como texto. Isso permite que as ViTs capturem relações espaciais e semânticas em imagens.

As camadas de autoatenção funcionam da seguinte forma:

• Entrada Fracionada: Na ViT, a imagem de entrada é dividida em patches (pequenas partes retangulares) que são tratados como sequências. Cada patch é incorporado em um espaço vetorial.
• Autoatenção Multi-Cabeça: As camadas de autoatenção são compostas por várias cabeças de autoatenção que operam paralelamente. Cada cabeça aprende a atenção em relação a diferentes aspectos da entrada.
• Aprendizado de Pesos: Em cada cabeça de autoatenção, os pesos são aprendidos para determinar a importância das relações entre os patches. Os pesos refletem a similaridade entre os patches, permitindo que o modelo dê mais peso a regiões relevantes da imagem.
• Composição do Contexto: Os resultados das várias cabeças de autoatenção são combinados para formar um contexto global que captura as interações entre todos os patches da imagem.
• Processamento em Camadas: Várias camadas de autoatenção são empilhadas em uma arquitetura, permitindo que o modelo processe informações em várias etapas e capture características complexas.

No artigo acadêmico Vision Transformer for Small-Size Datasets, os autores se propuseram a resolver o problema do viés indutivo de localidade em ViTs.

As ideias principais são:

• Tokenização de correção por deslocamento
• Autoatenção da localidade

Este exemplo implementa as ideias do artigo. Grande parte deste exemplo é inspirada na classificação de imagens com ViT.

Observação: Este exemplo requer o TensorFlow 2.6 ou superior, bem como os complementos do TensorFlow, que podem ser instalados usando o seguinte comando:

pip install -qq -U tensorflow-addons

Importar as bibliotecas

Importe as bibliotecas necessárias.

import math
import numpy as np
import tensorflow as tf
from tensorflow import keras
import tensorflow_addons as tfa
import matplotlib.pyplot as plt
from tensorflow.keras import layers

Configurar o Keras

Configure a semente para reproduzibilidade.

SEED = 42
keras.utils.set_random_seed(SEED)

Preparar dados

Prepare os dados com o número de classes e dimensões de entrada.

NUM_CLASSES = 100
DIMENSOES_ENTRADA = (32, 32, 3)

Carregar dados(ViT)

Carregue os conjuntos de dados e alvos de treino e teste, usando o dataset CIFAR-100.

(dados_treino, alvos_treino), (dados_teste, alvos_teste) = keras.datasets.cifar100.load_data()

Imprima as dimensões dos dados.

print(f"dados_treino shape: {dados_treino.shape} - alvos_treino shape: {alvos_treino.shape}")
print(f"dados_teste shape: {dados_teste.shape} - alvos_teste shape: {alvos_teste.shape}")

dados_treino shape: (50000, 32, 32, 3) - alvos_treino shape: (50000, 1)
dados_teste shape: (10000, 32, 32, 3) - alvos_teste shape: (10000, 1)

Configurar os hiperparâmetros

Os hiperparâmetros cumprimem diferentes papéis, sinta-se à vontade para ajustar os hiperparâmetros.

# Dados
TAM_BUFFER = 512
TAM_LOTE = 256

# Aumento de dados
TAM_IMAGEM = 72
TAM_CORRECAO = 6
NUM_CORRECOES = (TAM_IMAGEM // TAM_CORRECAO) ** 2

# Otimizador
TAXA_APRENDIZADO = 0.001
PESO_DECAIMENTO = 0.0001

# Treinamento
EPISODIOS = 50

# Arquitetura
NORMA_CAMADA_EPS = 1e-6
CAMADAS_TRANFORMACAO = 8
DIM_PROJECAO = 64
NUM_CABECAS = 4
UNIDADES_TRANSFORMADORAS = [
    DIM_PROJECAO * 2,
    DIM_PROJECAO,
]
UNIDADES_CABECA_MLP = [2048, 1024]

Aumentar dados

Um trecho do jornal:

"De acordo com o DeiT, várias técnicas são necessárias para treinar ViTs com eficácia.

Assim, aplicamos aumentos de dados como CutMix, Mixup, Auto Augment, Repeated Augment a todos os modelos."

Neste exemplo, focaremos apenas na novidade da abordagem e não na reprodução dos resultados do artigo.

Por esta razão, não utilizamos os esquemas de aumento de dados mencionados.

Sinta-se à vontade para adicionar ou remover o pipeline de aumento.

aumento_dados = keras.Sequential(
    [
        layers.Normalization(),
        layers.Resizing(TAM_IMAGEM, TAM_IMAGEM),
        layers.RandomFlip("horizontal"),
        layers.RandomRotation(factor=0.02),
        layers.RandomZoom(height_factor=0.2, width_factor=0.2),
    ],
    name="data_augmentation",
)

# Calcule a média e a variância dos dados de treinamento para normalização.
aumento_dados.layers[0].adapt(dados_treino)

Implementar tokenização de correção por deslocamento (STP)

Em um pipeline ViT, as imagens de entrada são divididas em patchs que são então projetados linearmente em tokens.

A tokenização de correção por deslocamento (SPT - Shift Patch Tokenization) é introduzida para combater o baixo campo receptivo dos ViTs.

As etapas para SPT são as seguintes:

• Carregar a imagem.
• Deslocá-la em direções diagonais.
• Concatenar as imagens deslocadas diagonalmente com a imagem original.
• Extrair patchs das imagens concatenadas.
• Achatar a dimensão espacial de todas correcões.
• Normalizar em camadas os patchs achatados e então projetá-las.

class TokenizacaoCorrecaoDeslocamento(layers.Layer):
    def __init__(
        self,
        tamanho_imagem   = TAM_IMAGEM,
        tamanho_correcao = TAM_CORRECAO,
        num_correcoes    = NUM_CORRECOES,
        dim_projecao     = DIM_PROJECAO,
        vanilla          = False,
        **kwargs,
    ):
        super().__init__(**kwargs)
        self.vanilla             = vanilla  # Sinalizador para mudar para extrator de correção Vanilla.
        self.tamanho_imagem      = tamanho_imagem
        self.tamanho_correcao    = tamanho_correcao
        self.half_patch          = tamanho_correcao // 2
        self.correcoes_achatadas = layers.Reshape((num_correcoes, -1))
        self.projecao            = layers.Dense(units=dim_projecao)
        self.normas_camada       = layers.LayerNormalization(epsilon=NORMA_CAMADA_EPS)

    # Amortecedor de corte por deslocamento
    def crop_shift_pad(self, imagens, mode):
        # Construir as imagens diagonais deslocadas
        if mode == "left-up":
            altura_corte         = self.half_patch
            largura_corte        = self.half_patch
            altura_deslocamento  = 0
            largura_deslocamento = 0
        elif mode == "left-down":
            altura_corte         = 0
            largura_corte        = self.half_patch
            altura_deslocamento  = self.half_patch
            largura_deslocamento = 0
        elif mode == "right-up":
            altura_corte         = self.half_patch
            largura_corte        = 0
            altura_deslocamento  = 0
            largura_deslocamento = self.half_patch
        else:
            altura_corte         = 0
            largura_corte        = 0
            altura_deslocamento  = self.half_patch
            largura_deslocamento = self.half_patch

        # Corte as imagens deslocadas e preencha-as
        corte = tf.image.crop_to_bounding_box(
            imagens,
            offset_height = altura_corte,
            offset_width  = largura_corte,
            target_height = self.tamanho_imagem - self.half_patch,
            target_width  = self.tamanho_imagem - self.half_patch,
        )
        amortecedor_deslocamento = tf.image.pad_to_bounding_box(
            corte,
            offset_height = altura_deslocamento,
            offset_width  = largura_deslocamento,
            target_height = self.tamanho_imagem,
            target_width  = self.tamanho_imagem,
        )
        return amortecedor_deslocamento

    def call(self, imagens):
        if not self.vanilla:
            # Concatenar as imagens deslocadas com a imagem original
            imagens = tf.concat(
                [
                    imagens,
                    self.crop_shift_pad(imagens, mode="left-up"),
                    self.crop_shift_pad(imagens, mode="left-down"),
                    self.crop_shift_pad(imagens, mode="right-up"),
                    self.crop_shift_pad(imagens, mode="right-down"),
                ],
                axis=-1,
            )
        # Corrija as correcoes achatando e projetando as imagens
        correcoes = tf.image.extract_patches(
            images  = imagens,
            sizes   = [1, self.tamanho_correcao, self.tamanho_correcao, 1],
            strides = [1, self.tamanho_correcao, self.tamanho_correcao, 1],
            rates   = [1, 1, 1, 1],
            padding = "VALID",
        )
        correcoes_planas = self.correcoes_achatadas(correcoes)
        if not self.vanilla:
            # Normalize a camada dos <i>patchs</i> planos e projete-as linearmente
            tokens = self.normas_camada(correcoes_planas)
            tokens = self.projecao(tokens)
        else:
            # Projete linearmente os <i>patchs</i> planos
            tokens = self.projecao(correcoes_planas)
        return (tokens, correcoes)

Visualizar as correcões

O gráfico a seguir mostra as correções projetadas.

# Obtenha uma imagem aleatória do conjunto de dados de treinamento e redimensione a imagem
imagem = dados_treino[np.random.choice(range(dados_treino.shape[0]))]
imagem_redimensionada = tf.image.resize(
    tf.convert_to_tensor([imagem]), size=(TAM_IMAGEM, TAM_IMAGEM)
)

# Corretor Vanilla (<i>Vanilla Patch Maker</i>): Isso pega uma imagem e a divide em correcoes como no artigo ViT original
(token, correcao) = TokenizacaoCorrecaoDeslocamento(vanilla=True)(imagem_redimensionada / 255.0)
(token, correcao) = (token[0], correcao[0])

# Desloque a imagem em direções diagonais.
n = correcao.shape[0]
contagem = 1
plt.figure(figsize=(4, 4))
for linha in range(n):
    for coluna in range(n):
        plt.subplot(n, n, contagem)
        contagem = contagem + 1
        imagem = tf.reshape(correcao[linha][coluna], (TAM_CORRECAO, TAM_CORRECAO, 3))
        plt.imshow(imagem)
        plt.axis("off")
plt.show()

Tokenização de Patchs por Deslocamento (SPT - Shifted Patch Tokenization)

Esta camada pega a imagem e a desloca diagonalmente e depois extrai correções das imagens concatenadas.

(token, correcao) = TokenizacaoCorrecaoDeslocamento(vanilla=False)(imagem_redimensionada / 255.0)
(token, correcao) = (token[0], correcao[0])
n = correcao.shape[0]
imagens_deslocadas = ["ORIGINAL", "ESQUERDA-SUPERIOR", "ESQUERDA-INFERIOR", "DIREITA_SUPERIOR", "DIREITA-INFERIOR"]
for indice, nome in enumerate(imagens_deslocadas):
    print(nome)
    contagem = 1
    plt.figure(figsize=(4, 4))
    for linha in range(n):
        for coluna in range(n):
            plt.subplot(n, n, contagem)
            contagem = contagem + 1
            imagem = tf.reshape(correcao[linha][coluna], (TAM_CORRECAO, TAM_CORRECAO, 5 * 3))
            plt.imshow(imagem[..., 3 * indice : 3 * indice + 3])
            plt.axis("off")
    plt.show()

Implementar a camada de codificação de correção

Esta camada aceita correções projetadas e então adiciona informações posicionais a eles.

class CodificadorCorrecao(layers.Layer):
    def __init__(
        self, num_correcoes=NUM_CORRECOES, dim_projecao=DIM_PROJECAO, **kwargs
    ):
        super().__init__(**kwargs)
        self.num_correcoes = num_correcoes
        self.incorporacao_posicao = layers.Embedding(
            input_dim=num_correcoes, output_dim=dim_projecao
        )
        self.posicoes = tf.range(start=0, limit=self.num_correcoes, delta=1)

    def call(self, correcoes_codificadas):
        posicoes_codificadas = self.incorporacao_posicao(self.posicoes)
        correcoes_codificadas = correcoes_codificadas + posicoes_codificadas
        return correcoes_codificadas

Implementar autoatenção local

A equação de atenção regular é indicada abaixo.

atenção(Q,K,V) = softmax(QK^T/sqrt(dk))V

• O módulo de atenção recebe uma consulta, chave e valor.
• Primeiro, calculamos a semelhança entre a consulta e a chave por meio de um produto escalar.
• Em seguida, o resultado é dimensionado pela raiz quadrada da dimensão principal.
• A escala evita que a função softmax tenha um gradiente excessivamente pequeno.
• Softmax é então aplicado ao produto escalar escalado para produzir os pesos de atenção.
• O valor é então modulado através dos pesos de atenção.

Na autoatenção, consulta, chave e valor vêm da mesma entrada.

O produto escalar resultaria em grandes relações de auto-token, em vez de relações entre tokens.

Isso também significa que o softmax oferece probabilidades mais altas às relações auto-token do que às relações inter-token.

Para combater isso, os autores propõem mascarar a diagonal do produto escalar. Dessa forma, forçamos o módulo de atenção a prestar mais atenção às relações entre tokens.

O fator de escala é uma constante no módulo de atenção regular.

Isto atua como um 'termo de temperatura' que pode modular a função softmax.

Os autores sugerem um termo de temperatura que pode ser aprendido em vez de uma constante.

As duas dicas acima tornam-se a Autoatenção da Localidade.

Subclassificamos layers.MultiHeadAttention e implementamos a temperatura treinável.

A máscara de atenção é construída posteriormente.

class AtencaoMultiCabecaLSA(tf.keras.layers.MultiHeadAttention):
    def __init__(self, **kwargs):
        super().__init__(**kwargs)
        # O termo de temperatura treinável. O valor inicial
        # é a raiz quadrada da dimensão principal.
        self.tau = tf.Variable(math.sqrt(float(self._key_dim)), trainable=True)

    def _compute_attention(self, consulta, chave, valor, attention_mask=None, training=None):
        consulta = tf.multiply(consulta, 1.0 / self.tau)
        escores_atencao = tf.einsum(self._dot_product_equation, chave, consulta)
        escores_atencao = self._masked_softmax(escores_atencao, attention_mask)
        abandono_escores_atencao = self._dropout_layer(
            escores_atencao, training=training
        )
        saida_atencao = tf.einsum(
            self._combine_equation, abandono_escores_atencao, valor
        )
        return saida_atencao, escores_atencao

Implementar o MLP

Implemente o Perceptron Multi-Camadas (MLP - Multi-Layer Perceptron).

def mlp(x, unidades_escondidas, taxa_abandono):
    for unidades in unidades_escondidas:
        x = layers.Dense(unidades, activation=tf.nn.gelu)(x)
        x = layers.Dropout(taxa_abandono)(x)
    return x

# Construir a máscara de atenção diagonal
mascara_atencao_diagonal = 1 - tf.eye(NUM_CORRECOES)
mascara_atencao_diagonal = tf.cast([mascara_atencao_diagonal], dtype=tf.int8)

Implementar o ViT

def criar_classificador_vit(vanilla=False):
    entradas = layers.Input(shape=DIMENSOES_ENTRADA)

    # Dados aumentados
    aumentado = aumento_dados(entradas)

    # Criar patches.
    (tokens, _) = TokenizacaoCorrecaoDeslocamento(vanilla=vanilla)(aumentado)

    # Codificar correções.
    correcoes_codificadas = CodificadorCorrecao()(tokens)

    # Crie múltiplas camadas do bloco Transformer.
    for _ in range(CAMADAS_TRANFORMACAO):

        # Normalização de camada 1
        x1 = layers.LayerNormalization(epsilon=1e-6)(correcoes_codificadas)

        # Crie uma camada de atenção com várias cabeças.
        if not vanilla:
            saida_atencao = AtencaoMultiCabecaLSA(
                num_heads=NUM_CABECAS, key_dim=DIM_PROJECAO, dropout=0.1)(
                    x1, x1, attention_mask=mascara_atencao_diagonal)
        else:
            saida_atencao = layers.MultiHeadAttention(
                num_heads=NUM_CABECAS, key_dim=DIM_PROJECAO, dropout=0.1)(
                    x1, x1)

        # Pular conexão 1
        x2 = layers.Add()([saida_atencao, correcoes_codificadas])

        # Normalização de camada 2
        x3 = layers.LayerNormalization(epsilon=1e-6)(x2)

        # MLP - Multi-Layer Perceptron (Perceptron Multi-Camada)
        x3 = mlp(x3, unidades_escondidas=UNIDADES_TRANSFORMADORAS, taxa_abandono=0.1)
        
        # Pular conexão 2
        correcoes_codificadas = layers.Add()([x3, x2])

    # Crie um tensor [tamanho do lote, dimensão de projeção].
    representacao = layers.LayerNormalization(epsilon=1e-6)(correcoes_codificadas)
    representacao = layers.Flatten()(representacao)
    representacao = layers.Dropout(0.5)(representacao)

    # Adicionar MLP
    caracteristicas = mlp(representacao, unidades_escondidas=UNIDADES_CABECA_MLP, taxa_abandono=0.5)

    # Classificar as saídas.
    saidas = layers.Dense(NUM_CLASSES)(caracteristicas)

    # Criar o modelo Keras
    modelo = keras.Model(entradas=entradas, outputs=saidas)
    return modelo

Compilar, treinar e avaliar o modelo

class coseno_aquecimento(keras.optimizers.schedules.LearningRateSchedule):
    def __init__(
        self, taxa_base_aprendizado, total_passos, taxa_aprendizado_aquecimento, passos_aquecimento
    ):
        super().__init__()

        self.taxa_base_aprendizado = taxa_base_aprendizado
        self.total_passos = total_passos
        self.taxa_aprendizado_aquecimento = taxa_aprendizado_aquecimento
        self.passos_aquecimento = passos_aquecimento
        self.pi = tf.constant(np.pi)

    def __call__(self, step):
        if self.total_passos < self.passos_aquecimento:
            raise ValueError("Total_steps deve ser maior ou igual a passos_aquecimento.")

        cos_lr_recozido = tf.cos(
            self.pi
            * (tf.cast(step, tf.float32) - self.passos_aquecimento)
            / float(self.total_passos - self.passos_aquecimento)
        )
        taxa_aprendizado = 0.5 * self.taxa_base_aprendizado * (1 + cos_lr_recozido)

        if self.passos_aquecimento > 0:
            if self.taxa_base_aprendizado < self.taxa_aprendizado_aquecimento:
                raise ValueError(
                    "taxa_base_aprendizado deve ser maior ou igual a "
                    "taxa_aprendizado_aquecimento."
                )
            slope = (self.taxa_base_aprendizado - self.taxa_aprendizado_aquecimento) / self.passos_aquecimento
            taxa_aquecimento = slope * tf.cast(step, tf.float32) + self.taxa_aprendizado_aquecimento
            taxa_aprendizado = tf.where(step < self.passos_aquecimento, taxa_aquecimento, taxa_aprendizado)
        return tf.where(step > self.total_passos, 0.0, taxa_aprendizado, name="learning_rate")

A função executar_experimento() recebe um modelo e executa o treinamento.

def executar_experimento(modelo):
    total_passos = int((len(dados_treino) / TAM_LOTE) * EPISODIOS)
    percentagem_episodio_aquecimento = 0.10
    passos_aquecimento = int(total_passos * percentagem_episodio_aquecimento)
    scheduled_lrs = coseno_aquecimento(
        learning_rate_base   = TAXA_APRENDIZADO,
        warmup_steps         = total_passos,
        warmup_learning_rate = 0.0,
        warmup_steps         = passos_aquecimento,
    )

    otimizador = tfa.optimizers.AdamW(
        learning_rate = TAXA_APRENDIZADO,
        weight_decay  = PESO_DECAIMENTO
    )

    modelo.compile(
        optimizer = otimizador,
        loss      = keras.losses.SparseCategoricalCrossentropy(from_logits=True),
        metrics   = [
            keras.metrics.SparseCategoricalAccuracy(name="acuracia"),
            keras.metrics.SparseTopKCategoricalAccuracy(5, name="acuracia-top-5"),
        ],
    )

    historia = modelo.fit(
        x=dados_treino,
        y=alvos_treino,
        batch_size=TAM_LOTE,
        epochs=EPISODIOS,
        validation_split=0.1,
    )
    _, acuracia, acuracia_top_5 = modelo.evaluate(dados_teste, alvos_teste, batch_size=TAM_LOTE)
    print(f"Acurácia do teste: {round(acuracia * 100, 2)}%")
    print(f"Acurácia do teste top-5: {round(acuracia_top_5 * 100, 2)}%")

    return historia

Execute experimentos com o ViT Vanilla

vit = criar_classificador_vit(vanilla=True)
historia = executar_experimento(vit)

Epoch 1/50
176/176 [==============================] - 22s 83ms/step - loss: 4.4912 - acuracia: 0.0427 acuracia-top-5: 0.1549 - val_loss: 3.9409 - val_acuracia: 0.1030 - val_acuracia-top-5: 0.3036
Epoch 2/50
176/176 [==============================] - 14s 77ms/step - loss: 3.9749 - acuracia: 0.0897 acuracia-top-5: 0.2802 - val_loss: 3.5721 - val_acuracia: 0.1550 - val_acuracia-top-5: 0.4058
Epoch 3/50
176/176 [==============================] - 14s 77ms/step - loss: 3.7129 - acuracia: 0.1282 acuracia-top-5: 0.3601 - val_loss: 3.3235 - val_acuracia: 0.2022 - val_acuracia-top-5: 0.4788
Epoch 4/50
176/176 [==============================] - 14s 77ms/step - loss: 3.5518 - acuracia: 0.1544 acuracia-top-5: 0.4078 - val_loss: 3.2432 - val_acuracia: 0.2132 - val_acuracia-top-5: 0.5056
Epoch 5/50
176/176 [==============================] - 14s 77ms/step - loss: 3.4098 - acuracia: 0.1828 acuracia-top-5: 0.4471 - val_loss: 3.0910 - val_acuracia: 0.2462 - val_acuracia-top-5: 0.5376
Epoch 6/50
176/176 [==============================] - 14s 77ms/step - loss: 3.2835 - acuracia: 0.2037 acuracia-top-5: 0.4838 - val_loss: 2.9803 - val_acuracia: 0.2704 - val_acuracia-top-5: 0.5606
Epoch 7/50
176/176 [==============================] - 14s 77ms/step - loss: 3.1756 - acuracia: 0.2205 acuracia-top-5: 0.5113 - val_loss: 2.8608 - val_acuracia: 0.2802 - val_acuracia-top-5: 0.5908
Epoch 8/50
176/176 [==============================] - 14s 77ms/step - loss: 3.0585 - acuracia: 0.2439 acuracia-top-5: 0.5432 - val_loss: 2.8055 - val_acuracia: 0.2960 - val_acuracia-top-5: 0.6144
Epoch 9/50
176/176 [==============================] - 14s 77ms/step - loss: 2.9457 - acuracia: 0.2654 acuracia-top-5: 0.5697 - val_loss: 2.7034 - val_acuracia: 0.3210 - val_acuracia-top-5: 0.6242
Epoch 10/50
176/176 [==============================] - 14s 77ms/step - loss: 2.8458 - acuracia: 0.2863 acuracia-top-5: 0.5918 - val_loss: 2.5899 - val_acuracia: 0.3416 - val_acuracia-top-5: 0.6500
Epoch 11/50
176/176 [==============================] - 14s 77ms/step - loss: 2.7530 - acuracia: 0.3052 acuracia-top-5: 0.6191 - val_loss: 2.5275 - val_acuracia: 0.3526 - val_acuracia-top-5: 0.6660
Epoch 12/50
176/176 [==============================] - 14s 77ms/step - loss: 2.6561 - acuracia: 0.3250 acuracia-top-5: 0.6355 - val_loss: 2.5111 - val_acuracia: 0.3544 - val_acuracia-top-5: 0.6554
Epoch 13/50
176/176 [==============================] - 14s 77ms/step - loss: 2.5833 - acuracia: 0.3398 acuracia-top-5: 0.6538 - val_loss: 2.3931 - val_acuracia: 0.3792 - val_acuracia-top-5: 0.6888
Epoch 14/50
176/176 [==============================] - 14s 77ms/step - loss: 2.4988 - acuracia: 0.3594 acuracia-top-5: 0.6724 - val_loss: 2.3695 - val_acuracia: 0.3868 - val_acuracia-top-5: 0.6958
Epoch 15/50
176/176 [==============================] - 14s 77ms/step - loss: 2.4342 - acuracia: 0.3706 acuracia-top-5: 0.6877 - val_loss: 2.3076 - val_acuracia: 0.4072 - val_acuracia-top-5: 0.7074
Epoch 16/50
176/176 [==============================] - 14s 77ms/step - loss: 2.3654 - acuracia: 0.3841 acuracia-top-5: 0.7024 - val_loss: 2.2346 - val_acuracia: 0.4202 - val_acuracia-top-5: 0.7174
Epoch 17/50
176/176 [==============================] - 14s 77ms/step - loss: 2.3062 - acuracia: 0.3967 acuracia-top-5: 0.7130 - val_loss: 2.2277 - val_acuracia: 0.4206 - val_acuracia-top-5: 0.7190
Epoch 18/50
176/176 [==============================] - 14s 77ms/step - loss: 2.2415 - acuracia: 0.4100 acuracia-top-5: 0.7271 - val_loss: 2.1605 - val_acuracia: 0.4398 - val_acuracia-top-5: 0.7366
Epoch 19/50
176/176 [==============================] - 14s 77ms/step - loss: 2.1802 - acuracia: 0.4240 acuracia-top-5: 0.7386 - val_loss: 2.1533 - val_acuracia: 0.4428 - val_acuracia-top-5: 0.7382
Epoch 20/50
176/176 [==============================] - 14s 77ms/step - loss: 2.1264 - acuracia: 0.4357 acuracia-top-5: 0.7486 - val_loss: 2.1395 - val_acuracia: 0.4428 - val_acuracia-top-5: 0.7404
Epoch 21/50
176/176 [==============================] - 14s 77ms/step - loss: 2.0856 - acuracia: 0.4442 acuracia-top-5: 0.7564 - val_loss: 2.1025 - val_acuracia: 0.4512 - val_acuracia-top-5: 0.7448
Epoch 22/50
176/176 [==============================] - 14s 77ms/step - loss: 2.0320 - acuracia: 0.4566 acuracia-top-5: 0.7668 - val_loss: 2.0677 - val_acuracia: 0.4600 - val_acuracia-top-5: 0.7534
Epoch 23/50
176/176 [==============================] - 14s 77ms/step - loss: 1.9903 - acuracia: 0.4666 acuracia-top-5: 0.7761 - val_loss: 2.0273 - val_acuracia: 0.4650 - val_acuracia-top-5: 0.7610
Epoch 24/50
176/176 [==============================] - 14s 77ms/step - loss: 1.9398 - acuracia: 0.4772 acuracia-top-5: 0.7877 - val_loss: 2.0253 - val_acuracia: 0.4694 - val_acuracia-top-5: 0.7636
Epoch 25/50
176/176 [==============================] - 14s 78ms/step - loss: 1.9027 - acuracia: 0.4865 acuracia-top-5: 0.7933 - val_loss: 2.0584 - val_acuracia: 0.4606 - val_acuracia-top-5: 0.7520
Epoch 26/50
176/176 [==============================] - 14s 77ms/step - loss: 1.8529 - acuracia: 0.4964 acuracia-top-5: 0.8010 - val_loss: 2.0128 - val_acuracia: 0.4752 - val_acuracia-top-5: 0.7654
Epoch 27/50
176/176 [==============================] - 14s 77ms/step - loss: 1.8161 - acuracia: 0.5047 acuracia-top-5: 0.8111 - val_loss: 1.9630 - val_acuracia: 0.4898 - val_acuracia-top-5: 0.7746
Epoch 28/50
176/176 [==============================] - 13s 77ms/step - loss: 1.7792 - acuracia: 0.5136 acuracia-top-5: 0.8140 - val_loss: 1.9931 - val_acuracia: 0.4780 - val_acuracia-top-5: 0.7640
Epoch 29/50
176/176 [==============================] - 14s 77ms/step - loss: 1.7268 - acuracia: 0.5211 acuracia-top-5: 0.8250 - val_loss: 1.9748 - val_acuracia: 0.4854 - val_acuracia-top-5: 0.7708
Epoch 30/50
176/176 [==============================] - 14s 77ms/step - loss: 1.7115 - acuracia: 0.5298 acuracia-top-5: 0.8265 - val_loss: 1.9669 - val_acuracia: 0.4884 - val_acuracia-top-5: 0.7796
Epoch 31/50
176/176 [==============================] - 14s 77ms/step - loss: 1.6795 - acuracia: 0.5361 acuracia-top-5: 0.8329 - val_loss: 1.9428 - val_acuracia: 0.4972 - val_acuracia-top-5: 0.7852
Epoch 32/50
176/176 [==============================] - 14s 77ms/step - loss: 1.6411 - acuracia: 0.5448 acuracia-top-5: 0.8412 - val_loss: 1.9318 - val_acuracia: 0.4952 - val_acuracia-top-5: 0.7864
Epoch 33/50
176/176 [==============================] - 14s 77ms/step - loss: 1.6015 - acuracia: 0.5547 acuracia-top-5: 0.8466 - val_loss: 1.9233 - val_acuracia: 0.4996 - val_acuracia-top-5: 0.7882
Epoch 34/50
176/176 [==============================] - 14s 77ms/step - loss: 1.5651 - acuracia: 0.5655 acuracia-top-5: 0.8525 - val_loss: 1.9285 - val_acuracia: 0.5082 - val_acuracia-top-5: 0.7888
Epoch 35/50
176/176 [==============================] - 14s 77ms/step - loss: 1.5437 - acuracia: 0.5672 acuracia-top-5: 0.8570 - val_loss: 1.9268 - val_acuracia: 0.5028 - val_acuracia-top-5: 0.7842
Epoch 36/50
176/176 [==============================] - 14s 77ms/step - loss: 1.5103 - acuracia: 0.5748 acuracia-top-5: 0.8620 - val_loss: 1.9262 - val_acuracia: 0.5014 - val_acuracia-top-5: 0.7890
Epoch 37/50
176/176 [==============================] - 14s 77ms/step - loss: 1.4784 - acuracia: 0.5822 acuracia-top-5: 0.8690 - val_loss: 1.8698 - val_acuracia: 0.5130 - val_acuracia-top-5: 0.7948
Epoch 38/50
176/176 [==============================] - 14s 77ms/step - loss: 1.4449 - acuracia: 0.5922 acuracia-top-5: 0.8728 - val_loss: 1.8734 - val_acuracia: 0.5136 - val_acuracia-top-5: 0.7980
Epoch 39/50
176/176 [==============================] - 14s 77ms/step - loss: 1.4312 - acuracia: 0.5928 acuracia-top-5: 0.8755 - val_loss: 1.8736 - val_acuracia: 0.5150 - val_acuracia-top-5: 0.7956
Epoch 40/50
176/176 [==============================] - 14s 77ms/step - loss: 1.3996 - acuracia: 0.5999 acuracia-top-5: 0.8808 - val_loss: 1.8718 - val_acuracia: 0.5178 - val_acuracia-top-5: 0.7970
Epoch 41/50
176/176 [==============================] - 14s 77ms/step - loss: 1.3859 - acuracia: 0.6075 acuracia-top-5: 0.8817 - val_loss: 1.9097 - val_acuracia: 0.5084 - val_acuracia-top-5: 0.7884
Epoch 42/50
176/176 [==============================] - 14s 77ms/step - loss: 1.3586 - acuracia: 0.6119 acuracia-top-5: 0.8860 - val_loss: 1.8620 - val_acuracia: 0.5148 - val_acuracia-top-5: 0.8010
Epoch 43/50
176/176 [==============================] - 14s 77ms/step - loss: 1.3384 - acuracia: 0.6154 acuracia-top-5: 0.8911 - val_loss: 1.8509 - val_acuracia: 0.5202 - val_acuracia-top-5: 0.8014
Epoch 44/50
176/176 [==============================] - 14s 78ms/step - loss: 1.3090 - acuracia: 0.6236 acuracia-top-5: 0.8954 - val_loss: 1.8607 - val_acuracia: 0.5242 - val_acuracia-top-5: 0.8020
Epoch 45/50
176/176 [==============================] - 14s 78ms/step - loss: 1.2873 - acuracia: 0.6292 acuracia-top-5: 0.8964 - val_loss: 1.8729 - val_acuracia: 0.5208 - val_acuracia-top-5: 0.8056
Epoch 46/50
176/176 [==============================] - 14s 77ms/step - loss: 1.2658 - acuracia: 0.6367 acuracia-top-5: 0.9007 - val_loss: 1.8573 - val_acuracia: 0.5278 - val_acuracia-top-5: 0.8066
Epoch 47/50
176/176 [==============================] - 14s 77ms/step - loss: 1.2628 - acuracia: 0.6346 acuracia-top-5: 0.9023 - val_loss: 1.8240 - val_acuracia: 0.5292 - val_acuracia-top-5: 0.8112
Epoch 48/50
176/176 [==============================] - 14s 78ms/step - loss: 1.2396 - acuracia: 0.6431 acuracia-top-5: 0.9057 - val_loss: 1.8342 - val_acuracia: 0.5362 - val_acuracia-top-5: 0.8096
Epoch 49/50
176/176 [==============================] - 14s 77ms/step - loss: 1.2163 - acuracia: 0.6464 acuracia-top-5: 0.9081 - val_loss: 1.8836 - val_acuracia: 0.5246 - val_acuracia-top-5: 0.8044
Epoch 50/50
176/176 [==============================] - 14s 77ms/step - loss: 1.1919 - acuracia: 0.6541 acuracia-top-5: 0.9122 - val_loss: 1.8513 - val_acuracia: 0.5336 - val_acuracia-top-5: 0.8048
40/40 [==============================] - 1s 26ms/step - loss: 1.8172 - acuracia: 0.5310 acuracia-top-5: 0.8053
Acurácia do teste: 53.1%
Acurácia do teste top-5: 80.53%

Execute experimentos com Tokenização de Patchs por Deslocamento (SPT - Shifted Patch Tokenization) e autoatenção de localidade modificada ViT.

vit_sl = criar_classificador_vit(vanilla=False)
historia = executar_experimento(vit_sl)

Epoch 1/50
176/176 [==============================] - 23s 90ms/step - loss: 4.4889 - acuracia: 0.0450 acuracia-top-5: 0.1559 - val_loss: 3.9364 - val_acuracia: 0.1128 - val_acuracia-top-5: 0.3184
Epoch 2/50
176/176 [==============================] - 15s 85ms/step - loss: 3.9806 - acuracia: 0.0924 acuracia-top-5: 0.2798 - val_loss: 3.6392 - val_acuracia: 0.1576 - val_acuracia-top-5: 0.4034
Epoch 3/50
176/176 [==============================] - 15s 84ms/step - loss: 3.7713 - acuracia: 0.1253 acuracia-top-5: 0.3448 - val_loss: 3.3892 - val_acuracia: 0.1918 - val_acuracia-top-5: 0.4622
Epoch 4/50
176/176 [==============================] - 15s 85ms/step - loss: 3.6297 - acuracia: 0.1460 acuracia-top-5: 0.3859 - val_loss: 3.2856 - val_acuracia: 0.2194 - val_acuracia-top-5: 0.4970
Epoch 5/50
176/176 [==============================] - 15s 85ms/step - loss: 3.4955 - acuracia: 0.1706 acuracia-top-5: 0.4239 - val_loss: 3.1359 - val_acuracia: 0.2412 - val_acuracia-top-5: 0.5308
Epoch 6/50
176/176 [==============================] - 15s 85ms/step - loss: 3.3781 - acuracia: 0.1908 acuracia-top-5: 0.4565 - val_loss: 3.0535 - val_acuracia: 0.2620 - val_acuracia-top-5: 0.5652
Epoch 7/50
176/176 [==============================] - 15s 85ms/step - loss: 3.2540 - acuracia: 0.2123 acuracia-top-5: 0.4895 - val_loss: 2.9165 - val_acuracia: 0.2782 - val_acuracia-top-5: 0.5800
Epoch 8/50
176/176 [==============================] - 15s 85ms/step - loss: 3.1442 - acuracia: 0.2318 acuracia-top-5: 0.5197 - val_loss: 2.8592 - val_acuracia: 0.2984 - val_acuracia-top-5: 0.6090
Epoch 9/50
176/176 [==============================] - 15s 85ms/step - loss: 3.0348 - acuracia: 0.2504 acuracia-top-5: 0.5440 - val_loss: 2.7378 - val_acuracia: 0.3146 - val_acuracia-top-5: 0.6294
Epoch 10/50
176/176 [==============================] - 15s 84ms/step - loss: 2.9311 - acuracia: 0.2681 acuracia-top-5: 0.5704 - val_loss: 2.6274 - val_acuracia: 0.3362 - val_acuracia-top-5: 0.6446
Epoch 11/50
176/176 [==============================] - 15s 85ms/step - loss: 2.8214 - acuracia: 0.2925 acuracia-top-5: 0.5986 - val_loss: 2.5557 - val_acuracia: 0.3458 - val_acuracia-top-5: 0.6616
Epoch 12/50
176/176 [==============================] - 15s 85ms/step - loss: 2.7244 - acuracia: 0.3100 acuracia-top-5: 0.6168 - val_loss: 2.4763 - val_acuracia: 0.3564 - val_acuracia-top-5: 0.6804
Epoch 13/50
176/176 [==============================] - 15s 85ms/step - loss: 2.6476 - acuracia: 0.3255 acuracia-top-5: 0.6358 - val_loss: 2.3946 - val_acuracia: 0.3678 - val_acuracia-top-5: 0.6940
Epoch 14/50
176/176 [==============================] - 15s 85ms/step - loss: 2.5518 - acuracia: 0.3436 acuracia-top-5: 0.6584 - val_loss: 2.3362 - val_acuracia: 0.3856 - val_acuracia-top-5: 0.7038
Epoch 15/50
176/176 [==============================] - 15s 85ms/step - loss: 2.4620 - acuracia: 0.3632 acuracia-top-5: 0.6776 - val_loss: 2.2690 - val_acuracia: 0.4006 - val_acuracia-top-5: 0.7222
Epoch 16/50
176/176 [==============================] - 15s 85ms/step - loss: 2.4010 - acuracia: 0.3749 acuracia-top-5: 0.6908 - val_loss: 2.1937 - val_acuracia: 0.4216 - val_acuracia-top-5: 0.7338
Epoch 17/50
176/176 [==============================] - 15s 85ms/step - loss: 2.3330 - acuracia: 0.3911 acuracia-top-5: 0.7041 - val_loss: 2.1519 - val_acuracia: 0.4286 - val_acuracia-top-5: 0.7370
Epoch 18/50
176/176 [==============================] - 15s 85ms/step - loss: 2.2600 - acuracia: 0.4069 acuracia-top-5: 0.7171 - val_loss: 2.1212 - val_acuracia: 0.4356 - val_acuracia-top-5: 0.7460
Epoch 19/50
176/176 [==============================] - 15s 85ms/step - loss: 2.1967 - acuracia: 0.4169 acuracia-top-5: 0.7320 - val_loss: 2.0748 - val_acuracia: 0.4470 - val_acuracia-top-5: 0.7580
Epoch 20/50
176/176 [==============================] - 15s 85ms/step - loss: 2.1397 - acuracia: 0.4302 acuracia-top-5: 0.7450 - val_loss: 2.1152 - val_acuracia: 0.4362 - val_acuracia-top-5: 0.7416
Epoch 21/50
176/176 [==============================] - 15s 85ms/step - loss: 2.0929 - acuracia: 0.4396 acuracia-top-5: 0.7524 - val_loss: 2.0044 - val_acuracia: 0.4652 - val_acuracia-top-5: 0.7680
Epoch 22/50
176/176 [==============================] - 15s 85ms/step - loss: 2.0423 - acuracia: 0.4521 acuracia-top-5: 0.7639 - val_loss: 2.0628 - val_acuracia: 0.4488 - val_acuracia-top-5: 0.7544
Epoch 23/50
176/176 [==============================] - 15s 85ms/step - loss: 1.9771 - acuracia: 0.4661 acuracia-top-5: 0.7750 - val_loss: 1.9380 - val_acuracia: 0.4740 - val_acuracia-top-5: 0.7836
Epoch 24/50
176/176 [==============================] - 15s 84ms/step - loss: 1.9323 - acuracia: 0.4752 acuracia-top-5: 0.7848 - val_loss: 1.9461 - val_acuracia: 0.4732 - val_acuracia-top-5: 0.7768
Epoch 25/50
176/176 [==============================] - 15s 85ms/step - loss: 1.8913 - acuracia: 0.4844 acuracia-top-5: 0.7914 - val_loss: 1.9230 - val_acuracia: 0.4768 - val_acuracia-top-5: 0.7886
Epoch 26/50
176/176 [==============================] - 15s 84ms/step - loss: 1.8520 - acuracia: 0.4950 acuracia-top-5: 0.7999 - val_loss: 1.9159 - val_acuracia: 0.4808 - val_acuracia-top-5: 0.7900
Epoch 27/50
176/176 [==============================] - 15s 85ms/step - loss: 1.8175 - acuracia: 0.5046 acuracia-top-5: 0.8076 - val_loss: 1.8977 - val_acuracia: 0.4896 - val_acuracia-top-5: 0.7876
Epoch 28/50
176/176 [==============================] - 15s 85ms/step - loss: 1.7692 - acuracia: 0.5133 acuracia-top-5: 0.8146 - val_loss: 1.8632 - val_acuracia: 0.4940 - val_acuracia-top-5: 0.7920
Epoch 29/50
176/176 [==============================] - 15s 85ms/step - loss: 1.7375 - acuracia: 0.5193 acuracia-top-5: 0.8206 - val_loss: 1.8686 - val_acuracia: 0.4926 - val_acuracia-top-5: 0.7952
Epoch 30/50
176/176 [==============================] - 15s 85ms/step - loss: 1.6952 - acuracia: 0.5308 acuracia-top-5: 0.8280 - val_loss: 1.8265 - val_acuracia: 0.5024 - val_acuracia-top-5: 0.7996
Epoch 31/50
176/176 [==============================] - 15s 85ms/step - loss: 1.6631 - acuracia: 0.5379 acuracia-top-5: 0.8348 - val_loss: 1.8665 - val_acuracia: 0.4942 - val_acuracia-top-5: 0.7854
Epoch 32/50
176/176 [==============================] - 15s 85ms/step - loss: 1.6329 - acuracia: 0.5466 acuracia-top-5: 0.8401 - val_loss: 1.8364 - val_acuracia: 0.5090 - val_acuracia-top-5: 0.7996
Epoch 33/50
176/176 [==============================] - 15s 85ms/step - loss: 1.5960 - acuracia: 0.5537 acuracia-top-5: 0.8465 - val_loss: 1.8171 - val_acuracia: 0.5136 - val_acuracia-top-5: 0.8034
Epoch 34/50
176/176 [==============================] - 15s 85ms/step - loss: 1.5815 - acuracia: 0.5578 acuracia-top-5: 0.8476 - val_loss: 1.8020 - val_acuracia: 0.5128 - val_acuracia-top-5: 0.8042
Epoch 35/50
176/176 [==============================] - 15s 85ms/step - loss: 1.5432 - acuracia: 0.5667 acuracia-top-5: 0.8566 - val_loss: 1.8173 - val_acuracia: 0.5142 - val_acuracia-top-5: 0.8080
Epoch 36/50
176/176 [==============================] - 15s 85ms/step - loss: 1.5110 - acuracia: 0.5768 acuracia-top-5: 0.8594 - val_loss: 1.8168 - val_acuracia: 0.5124 - val_acuracia-top-5: 0.8066
Epoch 37/50
176/176 [==============================] - 15s 85ms/step - loss: 1.4890 - acuracia: 0.5816 acuracia-top-5: 0.8641 - val_loss: 1.7861 - val_acuracia: 0.5274 - val_acuracia-top-5: 0.8120
Epoch 38/50
176/176 [==============================] - 15s 85ms/step - loss: 1.4672 - acuracia: 0.5849 acuracia-top-5: 0.8660 - val_loss: 1.7695 - val_acuracia: 0.5222 - val_acuracia-top-5: 0.8106
Epoch 39/50
176/176 [==============================] - 15s 85ms/step - loss: 1.4323 - acuracia: 0.5939 acuracia-top-5: 0.8721 - val_loss: 1.7653 - val_acuracia: 0.5250 - val_acuracia-top-5: 0.8164
Epoch 40/50
176/176 [==============================] - 15s 85ms/step - loss: 1.4192 - acuracia: 0.5975 acuracia-top-5: 0.8754 - val_loss: 1.7727 - val_acuracia: 0.5298 - val_acuracia-top-5: 0.8154
Epoch 41/50
176/176 [==============================] - 15s 85ms/step - loss: 1.3897 - acuracia: 0.6055 acuracia-top-5: 0.8805 - val_loss: 1.7535 - val_acuracia: 0.5328 - val_acuracia-top-5: 0.8122
Epoch 42/50
176/176 [==============================] - 15s 85ms/step - loss: 1.3702 - acuracia: 0.6087 acuracia-top-5: 0.8828 - val_loss: 1.7746 - val_acuracia: 0.5316 - val_acuracia-top-5: 0.8116
Epoch 43/50
176/176 [==============================] - 15s 85ms/step - loss: 1.3338 - acuracia: 0.6185 acuracia-top-5: 0.8894 - val_loss: 1.7606 - val_acuracia: 0.5342 - val_acuracia-top-5: 0.8176
Epoch 44/50
176/176 [==============================] - 15s 85ms/step - loss: 1.3171 - acuracia: 0.6200 acuracia-top-5: 0.8920 - val_loss: 1.7490 - val_acuracia: 0.5364 - val_acuracia-top-5: 0.8164
Epoch 45/50
176/176 [==============================] - 15s 85ms/step - loss: 1.3056 - acuracia: 0.6276 acuracia-top-5: 0.8932 - val_loss: 1.7535 - val_acuracia: 0.5388 - val_acuracia-top-5: 0.8156
Epoch 46/50
176/176 [==============================] - 15s 85ms/step - loss: 1.2876 - acuracia: 0.6289 acuracia-top-5: 0.8952 - val_loss: 1.7546 - val_acuracia: 0.5320 - val_acuracia-top-5: 0.8154
Epoch 47/50
176/176 [==============================] - 15s 85ms/step - loss: 1.2764 - acuracia: 0.6350 acuracia-top-5: 0.8970 - val_loss: 1.7177 - val_acuracia: 0.5382 - val_acuracia-top-5: 0.8200
Epoch 48/50
176/176 [==============================] - 15s 85ms/step - loss: 1.2543 - acuracia: 0.6407 acuracia-top-5: 0.9001 - val_loss: 1.7330 - val_acuracia: 0.5438 - val_acuracia-top-5: 0.8198
Epoch 49/50
176/176 [==============================] - 15s 84ms/step - loss: 1.2191 - acuracia: 0.6470 acuracia-top-5: 0.9042 - val_loss: 1.7316 - val_acuracia: 0.5436 - val_acuracia-top-5: 0.8196
Epoch 50/50
176/176 [==============================] - 15s 85ms/step - loss: 1.2186 - acuracia: 0.6457 acuracia-top-5: 0.9066 - val_loss: 1.7201 - val_acuracia: 0.5486 - val_acuracia-top-5: 0.8218
40/40 [==============================] - 1s 30ms/step - loss: 1.6760 - acuracia: 0.5611 acuracia-top-5: 0.8227
Acurácia do teste: 56.11%
Acurácia do teste top-5: 82.27%

Notas Finais

Com a ajuda de Shifted Patch Tokenization e Locality Self Attention, obtivemos um modelo de 65% de acurácia no CIFAR100.

As ideias sobre estas técnicas são muito intuitivas e fáceis de implementar.

Os autores também abordam diferentes estratégias de mudança para SPT no suplemento do artigo.

Foi utilizada a plataforma de GPUs de Jarvislabs.ai para aceleração do algorítmo.

Este código primeiro carrega os dados de treinamento e teste do conjunto de dados MNIST.

O conjunto de dados MNIST é um conjunto de imagens de dígitos manuscritos.

O código normaliza os dados dividindo cada pixel por 255. Isto é feito para que todos os dados estejam na mesma escala.

Em seguida, o código cria um modelo de rede neural. Este modelo é uma rede neural simples com duas camadas ocultas, cada uma com 128 neurônios.

A camada de saída tem 10 neurônios, um para cada classe no conjunto de dados. O código então compila o modelo, definindo o otimizador, a função de perda e as métricas.

Em seguida, o código treina o modelo, alimentando os dados de treinamento.

Por fim, o código avalia o desempenho do modelo, alimentando os dados de teste.

O código imprime a acurácia do modelo, que é a porcentagem de imagens que o modelo classificou corretamente.

• import tensorflow as tf: Importa a biblioteca TensorFlow.
• from tensorflow.keras.models import Sequential: Importa a classe Sequential do módulo models da sub-biblioteca Keras do TensorFlow.
• from tensorflow.keras.layers import Dense, Flatten: Importa as camadas Dense e Flatten da sub-biblioteca Keras do TensorFlow.
• from tensorflow.keras.datasets import mnist: Importa o conjunto de dados MNIST, que é amplamente utilizado para tarefas de reconhecimento de dígitos manuscritos.

import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten
from tensorflow.keras.datasets import mnist

A classe Sequential é usada para criar uma sequência linear de camadas em uma rede neural.

A camada Dense é uma camada de neurônios completamente conectados, e a camada Flatten é usada para aplanar os dados de entrada.

• load_data(): Carrega o conjunto de dados MNIST e divide-o em conjuntos de treinamento e teste.
• dados_treino: Retorna as imagens de treinamento.
• alvos_treino: Retorna as etiquetas correspondentes.
• dados_teste: Retorna as imagens de teste.
• alvos_teste: Retorna as etiquetas de teste.

Carrega as imagens de gatos e cães:

(dados_treino, alvos_treino), (dados_teste, alvos_teste) = mnist.load_data()

Dê uma olhada nos dados.

Conjuntos de dados e alvos de treino.

Dados de treino:

print('*** Dados do conjunto de treino')
print(f'Tipo: {type(dados_treino)}')
print(f'Dims: {dados_treino.shape}')
print()
print(dados_treino)

*** Dados do conjunto de treino
Tipo: <class 'numpy.ndarray'>
Dims: (60000, 28, 28)

[[[0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  ...
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]]

 [[0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  ...
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]]

 [[0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  ...
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]]

 ...

 [[0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  ...
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]]

 [[0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  ...
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]]

 [[0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  ...
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]]]

Imprima apenas o primeiro elemento do conjunto de dados, para formar ideia do formato das imagens.

primeiro_dado_treino = dados_treino[0]
print(f'Tipo: {type(primeiro_dado_treino)}')
print(f'Dims: {primeiro_dado_treino.shape}')
print()
print(primeiro_dado_treino)

Tipo: <class 'numpy.ndarray'>
Dims: (28, 28)

[[  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
    0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
    0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
    0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
    0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
    0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   3  18  18  18 126 136
  175  26 166 255 247 127   0   0   0   0]
 [  0   0   0   0   0   0   0   0  30  36  94 154 170 253 253 253 253 253
  225 172 253 242 195  64   0   0   0   0]
 [  0   0   0   0   0   0   0  49 238 253 253 253 253 253 253 253 253 251
   93  82  82  56  39   0   0   0   0   0]
 [  0   0   0   0   0   0   0  18 219 253 253 253 253 253 198 182 247 241
    0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0  80 156 107 253 253 205  11   0  43 154
    0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0  14   1 154 253  90   0   0   0   0
    0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0 139 253 190   2   0   0   0
    0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0  11 190 253  70   0   0   0
    0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0  35 241 225 160 108   1
    0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0  81 240 253 253 119
   25   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0  45 186 253 253
  150  27   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0  16  93 252
  253 187   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0 249
  253 249  64   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0  46 130 183 253
  253 207   2   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0  39 148 229 253 253 253
  250 182   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0  24 114 221 253 253 253 253 201
   78   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0  23  66 213 253 253 253 253 198  81   2
    0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0  18 171 219 253 253 253 253 195  80   9   0   0
    0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0  55 172 226 253 253 253 253 244 133  11   0   0   0   0
    0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0 136 253 253 253 212 135 132  16   0   0   0   0   0   0
    0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
    0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
    0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
    0   0   0   0   0   0   0   0   0   0]]

Alvos de treino:

print('*** Alvos do conjunto de treino')
print(f'Tipo: {type(alvos_treino)}')
print(f'Dims: {alvos_treino.shape}')
print()
print(alvos_treino)

*** Alvos do conjunto de treino
Tipo: <class 'numpy.ndarray'>
Dims: (60000,)

[5 0 4 ... 5 6 8]

Os alvos são um conjunto de números inteiros entre 0 e 9.

Imprima apenas o primeiro elemento do conjunto de alvos, para formar ideia do formato das etiquetas.

primeiro_alvo_treino = alvos_treino[0]
print(f'Tipo: {type(primeiro_alvo_treino)}')
print(f'Dims: {primeiro_alvo_treino.shape}')
print()
print(primeiro_alvo_treino)

Tipo: <class 'numpy.uint8'>
Dims: ()

5

Conjuntos de dados e alvos de teste.

Dados de teste:

print('*** Dados do conjunto de teste')
print(f'Dimensões: {dados_teste.shape}')
print()
print(dados_teste)

*** Dados do conjunto de teste
Dimensões: (10000, 28, 28)

[[[0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  ...
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]]

 [[0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  ...
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]]

 [[0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  ...
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]]

 ...

 [[0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  ...
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]]

 [[0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  ...
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]]

 [[0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  ...
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]
  [0 0 0 ... 0 0 0]]]

Alvos de teste:

print('*** Alvos do conjunto de teste')
print(f'Dimensões: {alvos_teste.shape}')
print()
print(alvos_teste)

*** Alvos do conjunto de teste
Dimensões: (10000,)

[7 2 1 ... 4 5 6]

Normalize os dados de pixel das imagens dividindo-os por 255.0. Isso coloca os valores dos pixels no intervalo de 0 a 1.

dados_treino = dados_treino / 255.0
dados_teste = dados_teste / 255.0

Imprima apenas os primeiros elementos dos conjuntos de dados de treino, para formar ideia do formato normalizado das imagens.

print('*** Dados do conjunto de treino')
print(dados_treino[0])

*** Dados do conjunto de treino
[[0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.
  0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.
  0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.
  0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.
  0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.
  0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.01 0.07
  0.07 0.07 0.49 0.53 0.69 0.1  0.65 1.   0.97 0.5  0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.   0.   0.   0.   0.12 0.14 0.37 0.6  0.67 0.99
  0.99 0.99 0.99 0.99 0.88 0.67 0.99 0.95 0.76 0.25 0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.   0.   0.   0.19 0.93 0.99 0.99 0.99 0.99 0.99
  0.99 0.99 0.99 0.98 0.36 0.32 0.32 0.22 0.15 0.   0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.   0.   0.   0.07 0.86 0.99 0.99 0.99 0.99 0.99
  0.78 0.71 0.97 0.95 0.   0.   0.   0.   0.   0.   0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.   0.   0.   0.   0.31 0.61 0.42 0.99 0.99 0.8
  0.04 0.   0.17 0.6  0.   0.   0.   0.   0.   0.   0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.   0.   0.   0.   0.   0.05 0.   0.6  0.99 0.35
  0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.55 0.99 0.75
  0.01 0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.04 0.75 0.99
  0.27 0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.14 0.95
  0.88 0.63 0.42 0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.32
  0.94 0.99 0.99 0.47 0.1  0.   0.   0.   0.   0.   0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.
  0.18 0.73 0.99 0.99 0.59 0.11 0.   0.   0.   0.   0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.
  0.   0.06 0.36 0.99 0.99 0.73 0.   0.   0.   0.   0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.
  0.   0.   0.   0.98 0.99 0.98 0.25 0.   0.   0.   0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.
  0.18 0.51 0.72 0.99 0.99 0.81 0.01 0.   0.   0.   0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.15 0.58
  0.9  0.99 0.99 0.99 0.98 0.71 0.   0.   0.   0.   0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.09 0.45 0.87 0.99
  0.99 0.99 0.99 0.79 0.31 0.   0.   0.   0.   0.   0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.   0.   0.   0.   0.09 0.26 0.84 0.99 0.99 0.99
  0.99 0.78 0.32 0.01 0.   0.   0.   0.   0.   0.   0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.   0.   0.07 0.67 0.86 0.99 0.99 0.99 0.99 0.76
  0.31 0.04 0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.22 0.67 0.89 0.99 0.99 0.99 0.99 0.96 0.52 0.04
  0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.53 0.99 0.99 0.99 0.83 0.53 0.52 0.06 0.   0.
  0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.
  0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.
  0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.
  0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0.  ]]

Crie o modelo usando a classe Sequential.

• modelo = Sequential: Cria um modelo de rede neural sequencial, onde as camadas são empilhadas uma após a outra na ordem em que são adicionadas.
• modelo.add(Flatten(input_shape=(28, 28))): Adiciona uma camada Flatten que transforma a matriz 2D das imagens (28x28 pixels) em um vetor 1D de 784 elementos.
• modelo.add(Dense(128, activation='relu')): Adiciona uma camada Dense com 128 neurônios e função de ativação ReLU (Rectified Linear Unit).
• modelo.add(Dense(10, activation='softmax')): Adiciona uma camada Dense com 10 neurônios, correspondendo às 10 classes possíveis no conjunto de dados MNIST, e utiliza a função de ativação softmax para produzir probabilidades de classe.

modelo = Sequential()
modelo.add(Flatten(input_shape=(28, 28)))
modelo.add(Dense(128, activation='relu'))
modelo.add(Dense(10, activation='softmax'))

Compile o modelo.

Defina o otimizador como 'adam', a função de perda como 'sparse_categorical_crossentropy' (adequada para tarefas de classificação multiclasse) e a métrica 'accuracy' de avaliação da precisão.

modelo.compile(
    optimizer='adam',
    loss='sparse_categorical_crossentropy',
    metrics=['accuracy'])

Treine o modelo.

Use os dados de treinamento (dados_treino e alvos_treino) por 10 episódios (épocas), ajustando os pesos da rede neural para minimizar a função de perda.

modelo.fit(dados_treino, alvos_treino, epochs=10)

Avalie o desempenho do modelo.

Use o conjunto de dados de teste (dados_teste e alvos_teste), retorna a pontuação, que inclui a perda e a precisão no conjunto de teste.

escore = modelo.evaluate(dados_teste, alvos_teste)

Imprima a acurácia do modelo, que é a porcentagem de imagens que o modelo classificou corretamente.

print(f'Acurácia ... : {escore[1]:.4f}')
print(f'Perda....... : {escore[0]:.4f}')

Acurácia ... : 0.9785
Perda....... : 0.0814

No exemplo fornecido, um modelo de rede neural foi treinado para realizar a tarefa de classificação de dígitos manuscritos usando o conjunto de dados MNIST.

Após o treinamento, foram obtidos dois valores essenciais: a perda (loss) e a precisão (accuracy).

A interpretação desses valores depende do contexto da tarefa específica, e eles são cruciais para avaliar o desempenho do modelo.

A perda é uma medida que indica o quão bem o modelo está performando na tarefa. Neste caso, a perda apresentou um valor de aproximadamente 0.08, o que é considerado baixo.

A perda é uma métrica relativa que deve ser interpretada em comparação com outros modelos ou referências específicas.

Em um cenário de classificação de dígitos MNIST, uma perda baixa é um sinal positivo, indicando que o modelo está fazendo previsões precisas.

Além disso, a acurácia ( ou precisão), que é uma métrica que expressa a porcentagem de classificações corretas em relação ao total de amostras no conjunto de teste, também foi calculada.

No exemplo, a precisão foi de cerca de 97.83%, o que é considerado uma precisão muito boa para a tarefa de classificação de dígitos MNIST.

No entanto, assim como a perda, a precisão é relativa ao contexto da tarefa.

Os valores de perda e precisão obtidos no exemplo são indicativos de um bom desempenho do modelo para a tarefa em questão, que é a classificação de dígitos manuscritos do MNIST.

No entanto, é fundamental considerar o contexto específico da tarefa e as expectativas de desempenho ao interpretar esses valores.

Em algumas tarefas, uma precisão de quase 98% e uma perda de 0.08 podem ser consideradas excelentes, enquanto em outras, esses valores podem ser insuficientes.

Portanto, a avaliação do desempenho do modelo deve sempre ser adaptada às necessidades e exigências do problema em questão.

São utilizadas as seguintes bibliotecas:

• cv2: OpenCV é uma biblioteca de processamento de imagens de código aberto. É usado para realizar uma variedade de tarefas relacionadas a imagens, como detecção de objetos, rastreamento de movimento e reconhecimento facial. OpenCV é uma ferramenta essencial para cientistas de dados e engenheiros que trabalham com imagens.
• tensorflow: TensorFlow é uma biblioteca de aprendizado de máquina de código aberto criada pelo Google. É usado para desenvolver e treinar modelos de aprendizado de máquina que podem ser usados em uma variedade de tarefas, como reconhecimento de imagens, reconhecimento de fala e tradução de idiomas.
• numpy: NumPy é uma biblioteca de matemática de alto desempenho para Python. É usado para criar e manipular matrizes, vetores e outros objetos matemáticos. NumPy é uma ferramenta essencial para cientistas de dados e engenheiros que precisam trabalhar com dados numéricos.
• label_map_util: LabelMapUtil é uma biblioteca de Python que ajuda a criar e manipular mapas de rótulos. Os mapas de rótulos são usados em muitos aplicativos de aprendizado de máquina para armazenar os rótulos de dados de treinamento. LabelMapUtil é uma ferramenta útil para cientistas de dados e engenheiros que trabalham com aprendizado de máquina.
• visualization_utils: VisualizationUtils é uma biblioteca de Python que ajuda a visualizar dados. VisualizationUtils fornece uma variedade de funções para criar gráficos, diagramas e outros tipos de visualizações de dados. É uma ferramenta útil para cientistas de dados e engenheiros que precisam comunicar suas descobertas para outras pessoas.
• threading: Threading é uma biblioteca de Python que ajuda a criar e gerenciar threads. As threads são uma maneira de executar várias tarefas ao mesmo tempo. Threading pode ser usado para melhorar o desempenho de aplicativos Python que precisam realizar várias tarefas.
• os: os é uma biblioteca Python que fornece acesso ao sistema operacional. Os pode ser usado para realizar uma variedade de tarefas relacionadas ao sistema operacional, como criar e manipular arquivos, acessar a rede e administrar processos. Os é uma ferramenta essencial para cientistas de dados e engenheiros que precisam interagir com o sistema operacional.

Essas bibliotecas são todas ferramentas valiosas para cientistas de dados e engenheiros. Podem ser usadas para realizar uma variedade de tarefas relacionadas a computação científica, aprendizado de máquina, processamento de imagens e sistema operacional.

Para instalar o Numpy, OpenCV e o TensorFlow, e suas dependências, use o pip:

pip show numpy
pip show opencv
pip show threading
pip show tensorflow
pip show tensorflow-object-detection-api
pip show protobuf

Para instalar o Numpy, OpenCV e o TensorFlow, e suas dependências, se estiverem faltantes, use o argumento install do pip:

pip install numpy
pip install opencv
pip install threading
pip install tensorflow
pip install tensorflow-object-detection-api
pip install protobuf

Se necessário, para instalar os módulos, execute o comando:

pip install tensorflow numpy cv2 threading 

Remova da instalação os módulos que não são necessários.

Código para importar as bibliotecas:

# 1 Importar bibliotecas
import tensorflow as tf
import numpy as np
from object_detection.utils import label_map_util
from object_detection.utils import visualization_utils as vis_util
import cv2
import threading
import os

A seguir são declaradas variáveis globais.

# 2 Declarar as variáveis globais
continuar = True
detectar = True
desenhar_deteccoes = True
redimensionar = False
cinza = False

A classe DetectorObjetos é responsável por detectar objetos em um frame.

Ela é inicializada com o caminho do modelo pré-treinado e a configuração do TensorFlow.

O método 'detectar_01()' recebe um frame e retorna os atributos calculados, usados para desenhar as detecções na janela de exibição.

O método 'desenhar_deteccoes()' é chamado a cada frame detectado, para desenhar as detecções na janela de exibição.

O método 'encerrar' é chamado automaticamente quando o objeto é destruído.

Ele fecha a janela de exibição do frame com as detecções.

O destrutor é chamado automaticamente quando o programa é encerrado.

Declarar a classe DetectorObjetos responsável por detectar objetos em um frame:

class DetectorObjetos:

Passo 3.1: Declarar o método __init__ construtor da classe detectora de objetos

    def __init__(
        self, root_path, model_path, label_path, max_detections=2,
        desenhar_deteccoes=True):
        #
        self.root_path = root_path
        self.model_path = model_path
        self.label_path = label_path
        self.max_detections = max_detections
        self.desenhar_deteccoes = desenhar_deteccoes
        self.deteccao_pronta = False
        self.frame_deteccao = None
        self.caixas = None
        self.classes = None
        self.escores = None
        self.iniciar()

Passo 3.2: Declarar o método 'iniciar', chamado no construtor, que carrega o modelo pré-treinado e a configuração do TensorFlow e cria a janela de exibição do frame com as detecções.

    def iniciar(self):
        self.carregar_modelo_pre_treinado()
        self.criar_janela()

Passo 3.3: Declarar o método 'encerrar' é chamado no destrutor, que fecha a janela de exibição do frame com as detecções. O destrutor é chamado automaticamente quando o objeto é destruído. Por exemplo, quando o programa é encerrado.

    def encerrar(self):
        self.fechar_janela()

Passo 3.4: Declarar o método 'criar_janela' cria a janela de exibição do frame com as detecções.

    def criar_janela(self):
        cv2.namedWindow('DETECTOR', cv2.WINDOW_NORMAL)

Passo 3.5: Declarar o método 'reposicionar_janela' move a janela de exibição do frame com as detecções.

    def reposicionar_janela(self,x,y):
        cv2.moveWindow('DETECTOR', x, y)

Passo 3.6: Declarar o método 'fechar_janela' fecha a janela de exibição do frame com as detecções.

    def fechar_janela(self):
        cv2.destroyWindow('DETECTOR')

Passo 3.7: Carrega o modelo pré-treinado e a configuração do TensorFlow:

    def carregar_modelo_pre_treinado(self):
        self.detector_grafico = tf.Graph()
        with self.detector_grafico.as_default():
            od_graph_def = tf.compat.v1.GraphDef()
            with tf.compat.v2.io.gfile.GFile(self.model_path,'rb') as f:
                serialized_graph = f.read()
                od_graph_def.ParseFromString(serialized_graph)
                tf.import_graph_def(od_graph_def, name='')
            label_map = label_map_util.load_labelmap(self.label_path)
            categories = label_map_util.convert_label_map_to_categories(label_map, max_num_classes=90, use_display_name=True)
            self.category_index = label_map_util.create_category_index(categories)

Passo 3.8: Executa a detecção de objetos no frame.

Essas linhas de código estão relacionadas à detecção de objetos em imagens usando um modelo de rede neural convolucional.

Cada uma das variáveis do tipo tensor retorna um array multidimensional de valores que representam diferentes aspectos da detecção de objetos.

Aqui está o que cada um desses tensores retorna:

• image_tensor: é um tensor que contém a imagem de entrada que será usada para a detecção de objetos.
• caixas_deteccao: é um tensor que contém as coordenadas das caixas delimitadoras (bounding boxes) que cercam os objetos detectados na imagem de entrada. Cada caixa delimitadora é representada por quatro valores: as coordenadas x e y do canto superior esquerdo e as coordenadas x e y do canto inferior direito.
• escores_deteccao: é um tensor que contém os escores de confiança (probabilidades) associados a cada caixa delimitadora. Esses escores indicam a probabilidade de que um objeto esteja presente dentro da caixa delimitadora correspondente. Quanto maior o escore, maior a probabilidade de que um objeto esteja presente.
• classes_deteccao: é um tensor que contém as classes dos objetos detectados nas caixas delimitadoras correspondentes. Cada classe é representada por um número inteiro, que pode ser mapeado para uma string correspondente que representa o nome da classe.
• num_deteccoes: é um tensor que contém o número de detecções de objetos encontrados na imagem. Esse valor é geralmente menor ou igual ao número máximo de objetos que o modelo foi treinado para detectar, que é uma configuração definida no momento do treinamento do modelo.

    def executar_deteccao(self,frame):
        # O frame da câmera é copiado para o frame de detecção
        # que será alterado para conter os retângulos de detecção
        self.frame_deteccao = frame.copy()

        dg = self.detector_grafico
        with dg.as_default():
            with tf.compat.v1.Session(graph=dg) as sess:
                
                # Redimensiona o frame para a detecção de objetos
                frame_expanded = sess.run(tf.expand_dims(self.frame_deteccao, axis=0))

                # Obtém os tensores de saída do modelo
                # image_tensor: é um tensor que contém a imagem de entrada que
                # será usada para a detecção de objetos.
                image_tensor = dg.get_tensor_by_name('image_tensor:0')

                # caixas_deteccao: é um tensor que contém as coordenadas das
                # caixas delimitadoras (bounding boxes)
                # que cercam os objetos detectados na imagem de entrada.
                caixas_deteccao = dg.get_tensor_by_name('detection_boxes:0')

                # escores_deteccao: é um tensor que contém os escores de 
                # confiança (probabilidades) associados a cada caixa delimitadora.   
                escores_deteccao = dg.get_tensor_by_name('detection_scores:0')

                # classes_deteccao: é um tensor que contém as classes dos objetos 
                # detectados nas caixas delimitadoras correspondentes.
                classes_deteccao = dg.get_tensor_by_name('detection_classes:0')

                # num_deteccoes: é um tensor que contém o número de
                # detecções de objetos encontrados na imagem.
                num_deteccoes = dg.get_tensor_by_name('num_detections:0')

                # Executa a detecção de objetos e retorna os valores dos tensores
                # caixas_deteccao, escores_deteccao, classes_deteccao e num_deteccoes
                # para os atributos caixas, escores, classes e num, respectivamente.
                (self.caixas, self.escores, self.classes, self.num) = sess.run(
                    [caixas_deteccao, escores_deteccao, classes_deteccao, num_deteccoes],
                    feed_dict={image_tensor: frame_expanded})

Passo 3.9: Desenha as caixas delimitadoras das classes detectadas no frame_deteccao

    def desenhar_retangulos(self):
        if self.desenhar_deteccoes:
            vis_util.visualize_boxes_and_labels_on_image_array(
                self.frame_deteccao,
                self.caixas,
                self.classes.astype(np.int32),
                self.escores,
                self.category_index,
                use_normalized_coordinates=True,
                line_thickness=2,
                max_boxes_to_draw=self.max_detections)

Passo 3.10: O método 'detector_01()' detecta objetos no frame redimensiona os tensores de saída para remover as dimensões adicionais filtra as detecções com pontuações acima de um limiar mínimo desenha as caixas delimitadoras das classes detectadas no frame_deteccao.

    def detector_01(self,frame):
        self.executar_deteccao(frame)
        self.redimensionar_tensores_01()
        self.desenhar_retangulos()

Passo 3.11: Remove dimensões adicionais dos tensores de saída e redimensiona os valores dos tensores para o tamanho do frame.

    def redimensionar_tensores_01(self):
        self.caixas = np.squeeze(self.caixas)
        self.escores = np.squeeze(self.escores)
        self.classes = np.squeeze(self.classes).astype(np.int32)
        # Filtra as detecções com pontuações acima de um limiar mínimo
        self.limiar = 0.5
        self.caixas = self.caixas[self.escores > self.limiar]
        self.classes = self.classes[self.escores > self.limiar]
        self.escores = self.escores[self.escores > self.limiar]

Passo 3.12: Filtra os resultados da detecção de objetos

    def detector_02(self):
        self.executar_deteccao()
        self.redimensionar_tensores_02()
        self.desenhar_retangulos()

Passo 3.13: Remove dimensões adicionais dos tensores de saída e redimensiona os valores dos tensores para o tamanho do frame

    def redimensionar_tensores_02(self):
        # altura e largura do frame
        height, width = self.frame_deteccao.shape[:2]
        self.caixas = np.squeeze(self.caixas)
        self.caixas[:, 0] *= height
        self.caixas[:, 1] *= width
        self.caixas[:, 2] *= height
        self.caixas[:, 3] *= width
        # Converte os valores dos tensores para inteiros
        self.caixas = self.caixas.astype(np.int32)
        self.escores = np.squeeze(self.escores).astype(np.float32)
        self.classes = np.squeeze(self.classes).astype(np.int32)
        # Filtra os resultados da detecção de objetos
        self.caixas = self.caixas[:self.max_detections]
        self.escores = self.escores[:self.max_detections]
        self.classes = self.classes[:self.max_detections]

class Camera:

A classe Camera controla uma câmera individual (webcam, arquivo de vídeo, etc).

Ela fornece acesso a imagens de vídeo em tempo real, bem como a localização de objetos detectados em cada quadro de vídeo.

A classe Camera é usada pelo programa principal para detectar objetos em um vídeo.

A classe Camera é uma classe abstrata. Ela não pode ser instanciada diretamente.

Em vez disso, você deve usar uma das subclasses concretas: WebcamCamera ou VideoCamera.

Passo 4.1: Método __init__ construtor da classe, inicializa a câmera

    # 4.1 Método __init__ construtor da classe 
    def __init__(self, cameras, id_camera, root_path, nome_video, redimensionar=(), cinza=False):
        # Atributos da classe
        self.cameras = cameras
        self.largura_maxima = cameras.largura_maxima
        self.altura_maxima = cameras.altura_maxima
        self.largura_borda = cameras.largura_borda
        self.altura_titulo = cameras.altura_titulo
        self.id_camera = id_camera
        self.redimensionar = redimensionar
        self.cinza = cinza
        self.root_path = root_path
        self.nome_video = nome_video
        self.video_path = os.path.join(root_path, nome_video)
        self.iniciar()

Passo 4.2: O método iniciar() inicializa a câmera, abre o arquivo de vídeo e cria a janela de vídeo.

    def iniciar(self):
        self.abrir_camera()
        self.criar_janela()

Passo 4.3: O método encerrar() fecha a câmera, fecha a janela de vídeo e fecha o arquivo de vídeo.

    def encerrar(self):
        self.fechar_janela()
        self.fechar_camera()

Passo 4.4: O método abrir_camera() abre o arquivo de vídeo e cria a janela de vídeo, e define o total de frames do arquivo de vídeo.0

    def abrir_camera(self):
        self.cap = cv2.VideoCapture(self.video_path)
        self.total_frames = int(self.cap.get(cv2.CAP_PROP_FRAME_COUNT))
        self.largura_cliente=int(self.cap.get(cv2.CAP_PROP_FRAME_WIDTH))
        self.altura_cliente=int(self.cap.get(cv2.CAP_PROP_FRAME_HEIGHT))
        if self.largura_maxima:
            self.altura_cliente = int(self.altura_cliente * self.largura_maxima / self.largura_cliente)
            self.largura_cliente = self.largura_maxima
        elif self.altura_maxima:
            self.largura_cliente = int(self.largura_cliente * self.altura_maxima // self.altura_cliente)
            self.altura_cliente = self.altura_maxima
        self.largura_janela = self.largura_cliente + (2 * self.largura_borda)
        self.altura_janela = self.altura_cliente + ((2 * self.largura_borda) + self.altura_titulo)

Passo 4.5: O método fechar_camera() fecha a câmera e fecha o arquivo de vídeo.

    def fechar_camera(self):
        self.cap.release()

Passo 4.6: Cria a janela de vídeo.

    def criar_janela(self):
        cv2.namedWindow(self.id_camera, cv2.WINDOW_NORMAL)
        cv2.resizeWindow(self.id_camera,self.largura_cliente, self.altura_cliente)

Passo 4.7: Move a janela de vídeo

    def reposicionar_janela(self, x, y):
        cv2.moveWindow(self.id_camera, x, y)

Passo 4.8: Fecha a janela de vídeo

    def fechar_janela(self):
        cv2.destroyWindow(self.id_camera)

Passo 4.9: Lê um frame do arquivo de vídeo e retorna ao primeiro frame caso chegue ao fim

    def ler_frame(self):
        ret, self.frame = self.cap.read()
        if not ret: 
            self.cap.set(cv2.CAP_PROP_POS_FRAMES, 0)
            ret, self.frame = self.cap.read()
        if ret: self.tratamentos_frame()
        return ret

Passo 4.10: Tratamento dos frames do arquivo de vídeo, redimensiona o frame e converte o frame para escala de cinza

    def tratamentos_frame(self):
        if self.redimensionar:
            self.frame = cv2.resize(self.frame,(self.redimensionar))
        if self.cinza:
            self.frame = cv2.cvtColor(self.frame, cv2.COLOR_BGR2GRAY)
            self.frame = cv2.cvtColor(self.frame, cv2.COLOR_GRAY2RGB)

class Cameras:

Passo 5.1: Método __init__

    def __init__(self, largura_maxima=0, altura_maxima=0, largura_borda=2, altura_titulo=30):
        self.largura_maxima = largura_maxima
        self.altura_maxima = altura_maxima
        self.largura_borda = largura_borda
        self.altura_titulo = altura_titulo
        self.lista_cameras: list[Camera] = []

Passo 5.2: Método __iter__()

    def __iter__(self):
        return iter(self.lista_cameras)

Passo 5.3: Método adicionar()

    def adicionar(self, pasta, nomes_cameras):
        for nome_camera in nomes_cameras:
            camera = Camera(cameras,str(len(self.lista_cameras)+1),pasta,nome_camera)
            self.lista_cameras.append(camera)

Passo 5.4: Método reposicionar_janelas()

    def reposicionar_janelas(self, x_inicial, y_inicial):
        x = x_inicial
        y = y_inicial
        max_y = 0
        linha = 0   
        for camera in cameras.lista_cameras:
            camera.reposicionar_janela(x,y)
            x += camera.largura_cliente
            if camera.altura_cliente > max_y:
                max_y = camera.altura_janela
            linha += 1
            if linha == 4:
                x = x_inicial
                y += max_y
                max_y = 0
                linha = 0
        if detectar:
            detector_objetos.reposicionar_janela(x,y)

Passo 5.5: Método iniciar()

    def iniciar(self):
        for camera in self.cameras:
            camera.iniciar()

Passo 5.6: Método encerrar()

    def encerrar(self):
        for camera in cameras.lista_cameras:
            camera.encerrar()   

Passo 6.1: Define o caminho para o diretório raiz do projeto.

ROOT_PATH = './'

cameras = Cameras(altura_maxima=400)
cameras.adicionar(ROOT_PATH,[
    #'video-1-360.mp4',
    #'video-ran.mp4',
    #'video-mulher-flores.mp4',
    #'video-pessoas-3.1280x720.mp4',
    'video-2-720.mp4'
    ])

Passo 6.2: Inicia a detecção

if detectar:

    OD_PATH = ROOT_PATH # "c:/cieda/object_detection/"

    # 6.2.1 Define o caminho para os arquivos de modelo pré-treinado e configuração
    MODEL_PATH = OD_PATH + 'object_detection/ssd_mobilenet_v1_coco_11_06_2017/frozen_inference_graph.pb'
    LABEL_PATH = OD_PATH + 'object_detection/data/mscoco_label_map.pbtxt'

    # 6.2.2 Define o máximo de detecções a serem exibidas
    MAX_DETECTIONS = 10

    # 6.2.3 Instancia e inicia o objeto detector
    detector_objetos = DetectorObjetos(
        ROOT_PATH, MODEL_PATH, LABEL_PATH, MAX_DETECTIONS,
        desenhar_deteccoes)
    def thread_funcao_detector_objetos():
        global continuar, detector_objetos
        while continuar:
            if detector_objetos.iniciar_deteccao:
                detector_objetos.iniciar_deteccao = False
                detector_objetos.detector_01(cameras.camera_atual.frame)
                detector_objetos.deteccao_pronta = True

    deteccao_liberada = True
    detector_objetos.iniciar_deteccao = False

    thread_deteccao_objetos = threading.Thread(target=thread_funcao_detector_objetos, args=())
    thread_deteccao_objetos.start()
else:
    thread_deteccao_objetos = None

Passo 6.3: Iniciar loop

cameras.reposicionar_janelas(100,100)

# 6.3 Loop infinito para processar cada frame do vídeo
num_camera = 0
while True:
    camera = cameras.lista_cameras[num_camera]
    cameras.camera_atual = camera
    # Lê frame com verificação se a leitura do frame foi bem sucedida
    if camera.ler_frame(): 

        # Exibe o frame com as detecções
        cv2.imshow(camera.id_camera,camera.frame)

        if detectar:
            if deteccao_liberada:
                deteccao_liberada = False
                detector_objetos.iniciar_deteccao = True
            if detector_objetos.deteccao_pronta:
                cv2.imshow('DETECTOR',detector_objetos.frame_deteccao)
                detector_objetos.deteccao_pronta = False
                deteccao_liberada = True

    num_camera += 1
    if num_camera == len(cameras.lista_cameras): num_camera = 0

    # Aguarda a tecla 'q' ser pressionada para encerrar o programa
    if cv2.waitKey(1) == ord('q'):
        break

Passo 6.4: Fecha a janela, encerra o detector, as câmeras e o programa

continuar = False
if detectar: detector_objetos.encerrar()
cameras.encerrar()